考虑库水粘滞性的拱坝动力响应分析

杨 柳，万学渊

（重庆市水利电力建筑勘测设计研究院，重庆 400000）

坝体-库水的耦合作用一直是大坝抗震分析的重要课题，尤其在近年混凝土拱坝修建越来越多的情况下，拱坝的抗震分析中流固耦合的影响更是不可忽视的重要内容[1]。对于流体粘性最早的理论认识是从牛顿著名的粘性流动试验开始的，液体的粘度一般随温度的升高而迅速减小。不考虑库水粘性时，库底采用全反射边界条件，但是在尽可能精确描述库水地震响应时，应当考虑水体粘性。势流体是符合欧拉方程的理想流体，而牛顿流体的动量方程是符合纳维-斯托克斯方程的考虑库水粘滞性的流体。本文用在流固耦合方面较有优势的有限元软件ADINA进行分析[2]，讨论库水粘滞性在计算过程中的影响。

1 有限元分析模型

五嘎冲水电站位于贵州省马别河上游平塘河段，坝顶高程1344 m，最大坝高为105 m，坝顶弦长612.5 m。有限元计算模型中拱坝坝高105 m，坝基范围及下游均取1.5倍坝高，根据黄耀英[3]、李瓒等人的研究结果，为充分反映水体的影响，水库长度向上游取三倍坝高。采用无质量地基模型进行计算。附加质量模型中将坝面上的动水压力施加到坝面节点上，其中材料参数：坝体体积弹性模量为20 GPa，密度为2400 kg/m3，泊松比为0.167基岩体积弹性模量为25 GPa，泊松比为0.25，水体密度为1000 kg/m3。模型如图1所示。

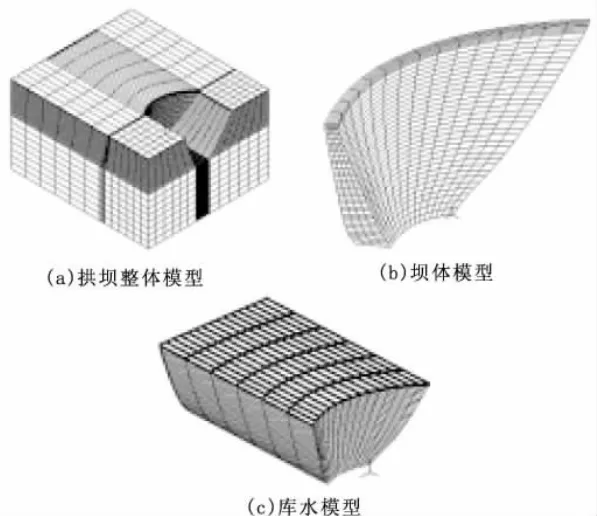
图1 五嘎冲拱坝模型

2 地震波的选取

选取水工建筑物抗震设计规范推荐的标准反应谱为目标谱，生成人工地震波作为拱坝坝基输入地震波，地震加速度峰值为0.1 g，地震动反应谱特征周期为0.20 s，相应地震基本烈度为7度。图2为所输入的规范波的顺河向加速度时程图。

3 考虑库水粘性的坝体动力反应分析

3.1 动水压力分析

图3 动水压力包络图（kPa）

图3 为两种模型的动水压力包络值分布图，其中(a)为利用牛顿流体计算所得到的动水压力包络图，(b)为利用势流体计算模型所得到的动水压力包络图，在两个等值线图中可以看出动水压力的分布规律一致，动水压力均沿坝高降低而增大。在坝体上部，坝面动水压力在各层拱圈处动水压力值基本一致，沿横河方向无变化，在坝体下部，左拱圈处动水压力较小，动水压力最大值出现在坝体底部右拱圈处，当坝体呈现非对称结构时，坝面的动水压力也会呈现非对称分布，可见动水压力不止是和坝高有关，和坝体结构也有关系，其中势流体计算模型动水压力最大值为94.16 kPa，而牛顿流体计算模型动水压力最大值为56.06 kPa，考虑库水粘滞性后，动水压力幅值降低40.46%。

图4 势流体和牛顿流体动水压力结果比较

图4 中分别选取两种方案的拱圈及拱冠梁动水压力进行对比，从拱圈的动水压力包络图中可以看出，(a)-(c)分别表示在1/4坝高处、1/2坝高处、3/4坝高处拱圈的动水压力包络图，(a)中可以看出在坝体上部沿横河方向动水压力值基本不变，从(b)、(c)图中可以看出在坝体中下部沿横河方向动水压力值会发生波动，右拱处更大，在不考虑库水粘滞性的势流体模型中动水压力值的不对称更加明显。(d)为势流体动水压力值比牛顿流体动水压力值大，由此可得出考虑库水粘性作用会降低其动水压力。两种方案的拱冠梁动水压力沿坝高分布基本一致，动水压力最大值均出现在坝体底部。

3.2 坝体位移变形分析

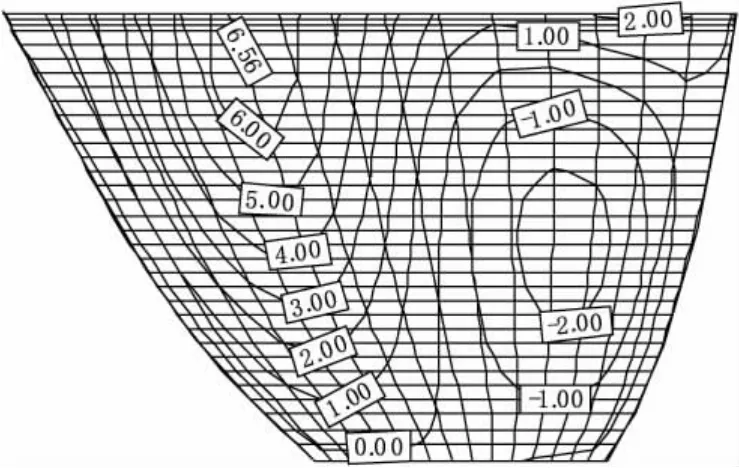
图5 牛顿流体模型横河向位移包络图(mm)

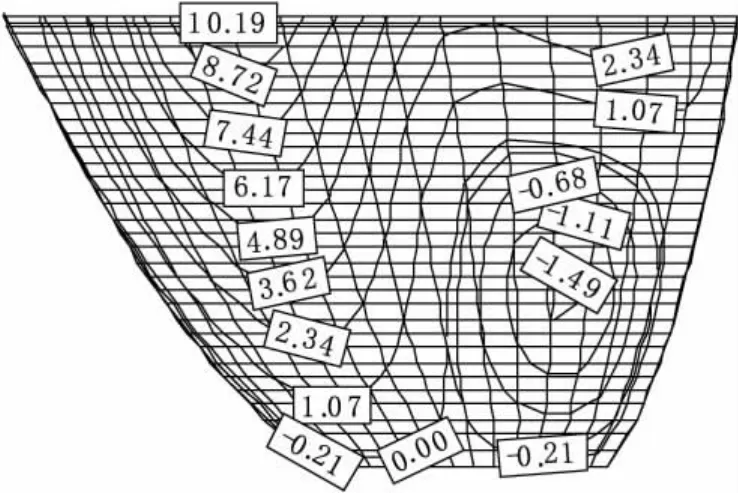
图6 势流体模型横河向位移包络图(mm)

从图5和图6中可以看出两种模型计算所得到的横河向变形规律一致，在坝体上部左拱圈处变形比较大且两种模型的变形值相差较大，在坝体其它部位变形值基本一致，在坝体顶部右拱圈处变形在2~3 mm之间。牛顿流体的横河向最大变形为6.56 mm，势流体的横河向最大变形为10.20 mm，幅值增大55.49%.可见库水粘滞性对横河向位移有较大影响。

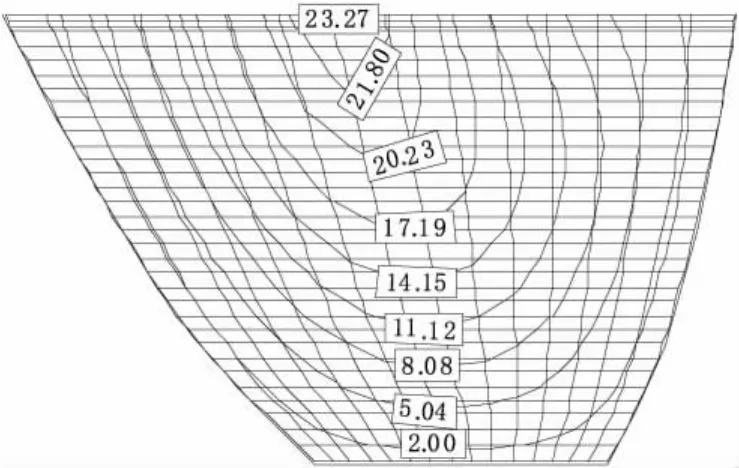
图7 牛顿流体模型顺河向位移(mm)

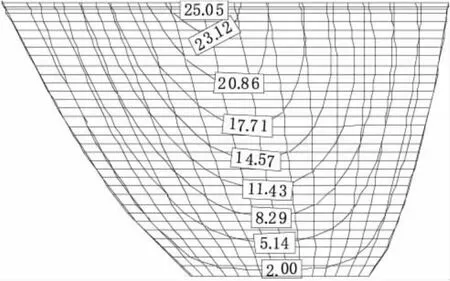
图8 势流体模型顺河向位移包络图(mm)

图7 和图8为两种模型的顺河向动静叠加包络值分布图，两种模型计算所得到的顺河向变形规律一致，整体上随坝高增大而增加，向下游面变形较大，最大值出现在坝体顶部拱冠梁处，牛顿流体的顺河向最大变形为23.27 mm，势流体的顺河向最大变形为25.05 mm，势流体模型的顺河向变形比牛顿流体的顺河向变形大。

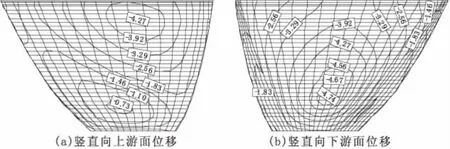
图9 牛顿流体模型竖直向位移(mm)

图10 流体模型竖直向位移(mm)

图9 和图10为两种模型的竖直向位移变形包络图，两种模型的上下游面分布规律相同，其中上游面竖直向最大变形出现在约95 m坝高处，上游面变形沿坝高减小而降低，且左岸变形降低速率较快，在坝址处变形较小，呈非对称分布，坝体左岸变形较小，右岸变形较大；下游面竖直向最大变形出现在约30 m坝高处，拱冠梁处变形比周围区域变形大。牛顿流体的竖直向最大变形为4.74 mm，势流体的竖直向最大变形为4.94 mm，势流体模型的竖直向变形大于牛顿流体的竖直向变形，但与横河向、顺河向位移的变化相比相差较小。

3.3 坝体拱向应力分析

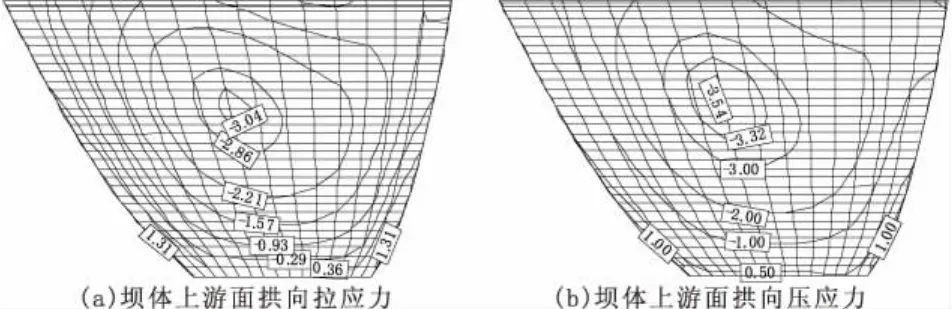
图11 牛顿流体模型拱向应力上游面动静叠加包络图（MPa）

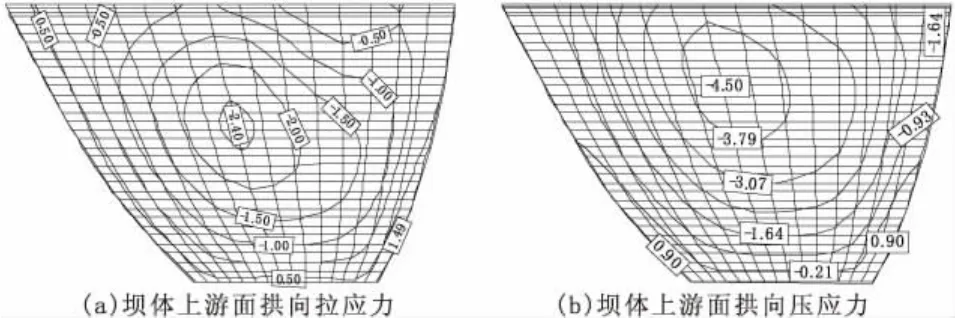
图12 势流体模型拱向应力上游面动静叠加包络图（MPa）

图11 和图12为牛顿流体和势流体模型的拱向应力图，两种模型的拱向应力动静叠加包络图分布规律一致，坝体拱向拉应力最大值出现在上游面左右坝肩处，拱向拉应力分布在上游面两岸坝肩和坝踵处，最大拉应力为1.49 MPa，牛顿流体模型的最大拉应力为1.47 MPa。

拱向压应力最大值出现在上游面坝体上部拱冠梁处和下游面坝体两岸坝肩处，势流体模型的最大压应力为4.80 MPa，牛顿流体模型的最大压应力为4.25 MPa。

3.4 坝体竖直向应力分析

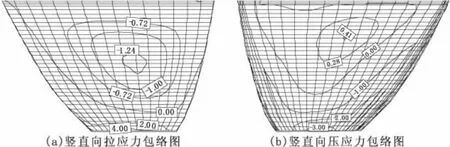
图13 牛顿流体模型竖直向应力动静叠加包络图（MPa）

图14 势流体模型竖直向应力动静叠加包络图（MPa）

从图13和图14中可以看出两种模型的竖直向应力分布规律相同，拉应力出现在左岸坝肩及1/5坝高处以下部位，在坝体下部拉应力随坝高的降低而增大，最大值均出现在上游面坝踵处，势流体模型的最大拉应力为4.15 MPa，牛顿流体模型的最大拉应力为4.26 MPa。

坝体上游面压应力最大值出现在1/2坝高的拱冠梁处，坝体下游面压应力随坝高的减小而增大，坝肩处压应力比拱冠梁处大，最大压应力出现在坝址处，势流体模型的最大压应力为4.53 MPa，牛顿流体模型的最大压应力为3.52 MPa。考虑库水粘滞性后，坝体的竖直向压应力幅值降低22.3%.

4 结论

通过ADINA的两种计算方法，利用五嘎冲拱坝模型，输入七度顺河向地震波，对考虑库水粘性的牛顿流体模型和不考虑库水粘性的势流体模型进行对比分析，两种计算方案所采用的库水粘性不同、计算方法有所差别、动力响应结果也有所不同，结论如下：

（1）两种计算方案的结果分布规律相同，考虑库水的粘滞性使其动水压力减小了40%左右，在坝体下部尤为明显。势流体的位移响应结果比牛顿流体的结果大，其中对横河向位移和顺河向位移影响比较明显，尤其是横河向位移的增幅达到50%左右，而对竖直向位移的影响较小，在整个坝体上不考虑粘滞性，其增幅仅在10%左右。是否考虑库水的粘滞性对坝体的应力反应也有一定的影响，其中对坝体的拱向拉应力影响较小，但考虑库水粘滞性后，坝体拱向压应力有所减小。库水粘滞性对坝体的竖直向拉应力影响较小，两种模型的差值基本在0.1 MPa左右，但对坝体的竖直向压应力影响较大，幅值降低约22.3%.

（2）在计算求解过程中，势流体模型有流体速度势和结构位移两个未知量，而牛顿流体模型有流体速度势、压力、位移和结构位移四个未知量，计算更为复杂。鉴于库水符合势流体假定，且势流体计算结果规律与牛顿流体计算结果的规律一致，在进行坝库耦合作用分析时，势流体模型优于牛顿流体模型，其计算结果更加有效。

[1]邱流潮，张立翔.地震作用下拱坝--库水耦合振动动水压力分析[J].水动力学研究与进展A辑.2000,15(1):94-103.

[2]岳戈，梁宇白，陈晨，等.ADINA流体与流固耦合功能的高级应用[M].北京:人民交通出版社,2010:8-13.

[3]黄耀英，孙大伟，田斌.两种库水附加质量模型的重力坝动力响应研究[J].人民长江.2009,40(7):64-66.