陀螺定向在隧道盾构平面控制测量检核中的应用

谢友鹏，赵尘衍

(1.常州市测绘院，江苏 常州 213003； 2.常州市地理信息智能技术中心，江苏 常州 213003)

1 引 言

常州轨道交通1号线黄河路站-新区公园站隧道区间左线全长 1 364.64 m，线路特点为多曲线小半径，最小曲线半径为 300 m，整体呈“S”型走向。该区间长度较长，且为曲线段，为了保证顺利贯通，对平面控制测量精度提出了较高的要求[1]。

黄河路站-新区公园站区间左线隧道施工采用盾构法由黄河路站向新区公园站掘进。为了保证单向掘进隧道的贯通和各种构筑物的位置符合设计要求，必须要有可靠的控制测量技术作为保障[2]。该隧道内的盾构平面控制测量工作采用基于支导线形式的导线测量进行，受到地形条件的限制，支导线的边长一般较短[3]。特别是在由黄河路站始发的隧道前半段，受到小半径曲线隧道线型的影响，用于进行平面控制测量的支导线站数较多，边长较短，易造成测角误差的积累，进而可能导致洞内平面控制点点位横向误差偏大，对隧道的顺利贯通产生影响。

为了确保盾构平面控制测量成果质量，一方面在洞内导线初测完成之后进行复测工作，另一方面采用陀螺全站仪对洞内定向边坐标方位角进行检核，以确保其成果的可靠性。

2 洞内导线的布设与施测

黄河路站-新区公园站左线隧道盾构工作开始之前已在黄河路站车站底板上建造好两座强制对中观测墩，两个车站底板平面控制点分别命名为XBD和BYD，并已通过联系测量采用两井定向的方法测定好两点平面坐标。洞内导线点采用强制对中铝合金支架以交叉形式依次进行布设，点号命名以“ZT”作为标识。洞内导线布设情况如图1所示。

图1 洞内导线布设

导线测量严格按照《城市轨道交通工程测量规范》(GB 50308-2008)、《工程测量规范》(GB 50026-2007)以及《常州市轨道交通工程建设测量工作统一作业技术标准》中的相关技术要求执行。平面坐标系统采用常州轨道交通工程坐标系，导线测量仪器为徕卡TM30测量机器人，标称精度：测角0.5″，测距 0.6 mm+1 ppm。在各测站上对前后观测目标采用ATR自动照准并进行4个测回的水平角和斜距的观测，测量过程中对各项观测限差严格控制，保证外业采集数据的可靠性。

导线测量完成后，经过平差计算得到定向边ZT10-ZT9、ZT10-ZT11的初测与复测坐标方位角成果如表1所示。

导线测量计算所得定向边ZT10-ZT9、ZT10-ZT11坐标方位角成果 表1

两条定向边通过导线测量计算所得坐标方位角初测与复测成果较差满足《常州市轨道交通工程建设测量工作统一作业技术标准》中限差要求。

3 陀螺定向测量

3.1 测量原理

陀螺定向测量直接测定出的是陀螺北方向，其与真北方向及坐标北方向之间的关系如图2所示。

图2 三北方向关系示意图

图中AB为一条地面已知导线边，A为设站点，B为观测点。α真表示地理方位角，α坐表示坐标方位角，α陀表示陀螺方位角，γ表示子午线收敛角，子午线收敛角可通过设站点坐标查表计算得到。

仪器常数的测定对陀螺定向精度有很大影响，通过陀螺全站仪的运转和观测即可测定出已知边的陀螺方位角，进而计算得到仪器常数[4]：

β仪=α真-α陀

(1)

在地面已知边测定出仪器常数后即可用于计算隧道内定向边坐标方位角：

α坐′=α真′-γ′=β仪+α陀′-γ′

(2)

式中，β仪为测定好的仪器常数，α陀′为隧道内定向边陀螺方位角，γ′为隧道内测站处子午线收敛角。

3.2 测量实施

陀螺定向测量方法包括逆转点法、中天法、时差法、改化振幅法、三点测时法以及计时法等[6]。考虑到施工隧道内环境较为恶劣与复杂，本次测量采用的是对环境要求不高的中天法。中天法是通过测定陀螺灵敏部通过中天的时刻和摆幅来计算陀螺北方向，具有灵活、方便，观测人员在观测过程中可以应付外界来往人员及其他突发情况干扰的特点，可以较好地保证观测精度[5]。

本次测量检核工作在盾构距贯通面还有100环时进行。采用索佳GP3130/R3陀螺全站仪对隧道内ZT10-ZT9与ZT10-ZT11两条定向边的方位角进行检核。仪器标称精度：一次定向中误差±20″，测角精度2″，测距精度 2 mm+2 ppm。

在对隧道内定向边进行测量前首先需在地面已知边上进行仪器常数的测定，仪器常数测定完成后再将仪器移至井下，进行定向测量工作。定向测量工作完成后尽快返回地面，并在原先的已知边上再次进行仪器常数的测定工作。定向测量要求测前、测后的仪器常数测定各观测三测回，三测回间的陀螺方位角较差不大于25″，两次求得的仪器常数均值较差不大于15″；对定向边进行两次观测，每次观测三测回，两次观测计算所得的陀螺方位角均值较差应小于12″。

本次测量检核工作分为两天进行，分别完成初测、复测两次独立的陀螺定向测量作业流程。首先，在地面已知边上测量陀螺方位角，计算仪器常数。选择两个常州市轨道交通1号线平面控制测量卫星定位网中的控制点1G15和1G18构成的边作为仪器常数测定边，共观测三个测回，测定成果如表2所示。

初测测前仪器常数测定成果 表2

可得初测测前仪器常数均值为-4.6″。

测前仪器常数测定完成后立即将陀螺全站仪移至隧道内对ZT10-ZT9和ZT10-ZT11两条定向边进行定向测量。定向边陀螺方位角测量成果如表3所示。

ZT10-ZT9、ZT10-ZT11定向边陀螺方位角初测成果 表3

计算得到定向边ZT10-ZT9、ZT10-ZT11陀螺方位角均值分别为339°50′51.3″与178°32′40.3″。

隧道内定向测量完成后返回地面，重新在已知边1G15-1G18上测定仪器常数，测定成果如表4所示。

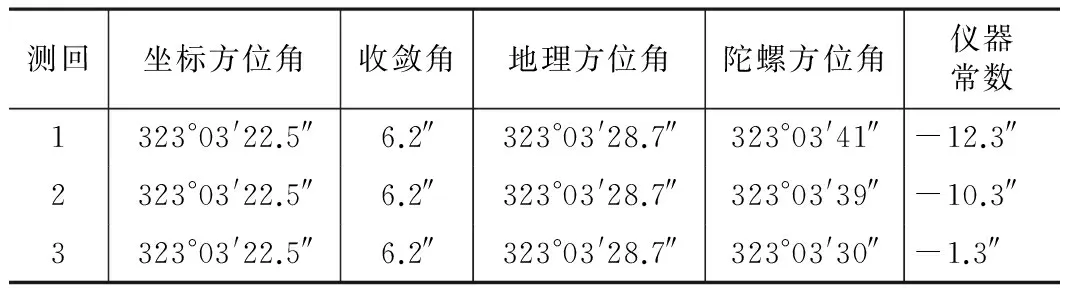
初测测后仪器常数测定成果 表4

可得初测测后仪器常数均值为-8.0″。

对测前、测后仪器常数值取平均得到最终的初测仪器常数-6.3″。进而通过式(2)可得定向边ZT10-ZT9、ZT10-ZT11陀螺定向坐标方位角如表5、表6所示。

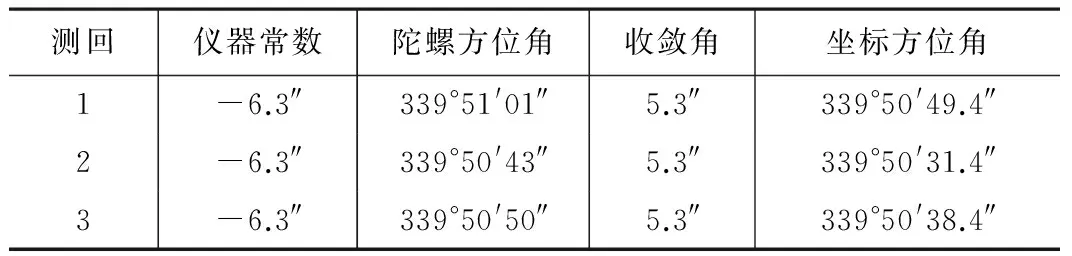
定向边ZT10-ZT9坐标方位角初测成果 表5

定向边ZT10-ZT11坐标方位角初测成果 表6

可得定向边ZT10-ZT9、ZT10-ZT11坐标方位角均值分别为339°50′39.7″与178°32′25.4″。

初测工作完成后于第二天重复同样的测量流程进行复测工作。测前、测后仪器常数测定成果如表7、表8所示。

复测测前仪器常数测定成果 表7

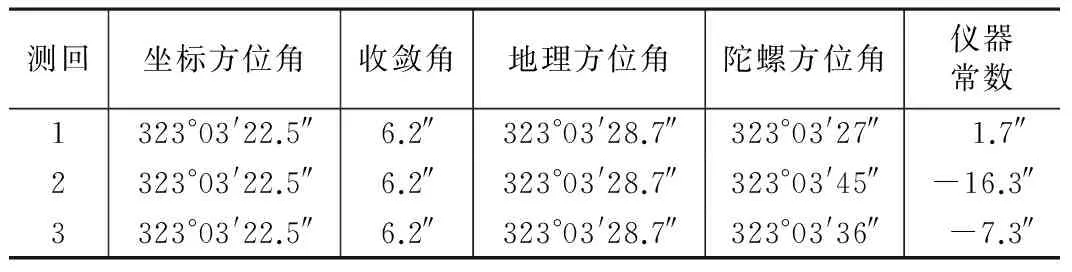
复测测后仪器常数测定成果 表8

可得仪器常数均值为-10.3″。

ZT10-ZT9、ZT10-ZT11两条定向边陀螺定向复测成果如表9、表10所示。

ZT10-ZT9定向边坐标方位角复测成果 表9

ZT10-ZT11定向边坐标方位角复测成果 表10

可得定向边ZT10-ZT9、ZT10-ZT11陀螺方位角均值分别为339°50′53.7″与178°32′37.0″，坐标方位角均值分别为339°50′38.1″与178°32′21.4″。

4 坐标方位角检核与分析

ZT10-ZT9、ZT10-ZT11两条定向边通过陀螺定向测量初测、复测所得陀螺方位角及其差值如表11所示。

ZT10-ZT9、ZT10-ZT11定向边陀螺方位角初测、复测成果 表11

两条定向边初测与复测陀螺方位角较差均满足作业限差要求，对初测与复测得到的两条定向边坐标方位角取平均可得最终陀螺定向测量成果：定向边ZT10-ZT9、ZT10-ZT11陀螺定向坐标方位角分别为339°50′38.9″与178°32′23.4″。

将陀螺定向成果与导线测量成果进行对比，如表12所示。

陀螺定向成果与导线测量成果对比表 表12

由上表可见，本次测量检核的两条定向边坐标方位角通过陀螺定向测量与导线测量所得成果差值均小于4″，可认为导线测量成果是可靠的，可供后续施工使用。

5 总 结

在地铁隧道盾构平面控制测量工作中，针对长区间多曲线的情况，在盾构推进至一半及盾构距贯通面100环等关键节点，除了对导线测量成果进行复测外，还应采用陀螺定向的方法对定向边坐标方位角进行检核，保证平面控制测量成果的可靠性，为隧道高精度贯通提供保障。

[1] 李学仕，郑成沛. 陀螺定向测量在广州地铁鱼大区间的应用与研究[J]. 铁道勘察，2008(1)：8～11+43.

[2] 罗三明，万文妮，高培芝等. 盾构工程竖井联系测量数据处理方法研究[J]. 大地测量与地球动力学，2007(5)：123～127.

[3] 马强. 基于加测陀螺定向边的井下支导线升级改造[J]. 测绘工程，2015，24(5)：57～62.

[4] 王佩贤，程飞，马国强. 陀螺定向中仪器常数的适用范围[J]. 测绘科学，2015(3)：112～114.

[5] 马军. 井下采用中天法进行陀螺定向的建议[J]. 矿山测量，1999(2)：48～49.

[6] 赵士恒. GP3130R3陀螺全站仪性能测试及数据处理研究[D]. 辽宁工程技术大学，2013.

[7] 甄洪斌，王国峰，杨学峰. 陀螺全站仪在济南市地下人防工程普查测量中的应用[J]. 城市勘测，2015(1)：140～141+145.

[8] 王佩贤，程飞，郑涛. 陀螺定向中几个常见问题的应用分析[J]. 测绘科学，2014(11)：118～120+125.

[9] 马强，陈荣，吴孟锋. 基于加测陀螺定向边的隧道工程贯通测量研究[J]. 城市勘测，2014(5)：136～139.

[10] 林玉池，孙占元，赵美蓉等. 中天法在陀螺智能寻北系统中的应用研究[J]. 机械工程学报，2003(8)：116～119.