城市轨道交通工程边长变形分析及超限处理方法探讨

赵亚波，王智，李勇，张洪德，薛慧艳

(青岛市勘察测绘研究院，山东 青岛 266032)

1 引 言

城市轨道交通工程在建设过程中，不管是前期的地面控制网测量，还是隧道开挖过程中的地下导线测量，测距边长都要经过高程归化改正和高斯投影两项改正[1]，高程归化改正的作用是将测距边长从观测平面高程面归算到城市轨道交通工程线路的平均高程面，若测距边所在平均高程面比城市轨道交通工程线路平均高程面要高，则测距边改算后变短，反之变长[2]；高斯投影改化的作用是将测距边两端点在椭球体上投影所形成的大地线改算到高斯投影面上的投影边长，不在中央子午线上的测距边，改正后边长均变长[3]。

我国现行规范要求，边长变形值不得超过 2.5 cm/km[4]。变形值在 2.5 cm/km之内，则用改正后的边长进行平差计算，若变形值超限，则需进行选取不同的高程投影面或中央子午线等方法进行改算[5]，本文分析了高程归化和高斯投影改化两项改正的数学公式，并以青岛地铁4号线为例分析了当城市轨道交通工程边长变形超限的处理方法。

2 数学模型

2.1 高程归化

(1)

由上式可得归化到城市轨道交通线路测区平均高程面上的测距边长度D的计算公式为[6]：

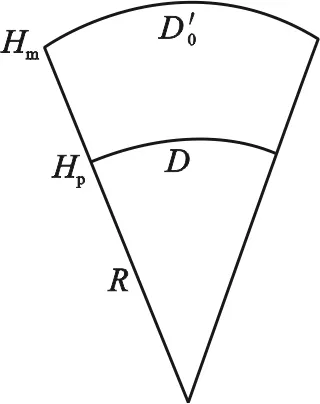
图1 高程归化示意图

(2)

式中：

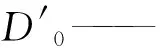
R——参考椭球体在测距边方向法截弧的曲率半径(m)；

Hp——城市轨道交通工程线路的平均高程(m)；

Hm——测距边两端点的平均高程(m)。

由上式可以看出，高程归化改算与测距边长度、所在高程面以及城市轨道交通工程线路的平均高程面有关。

2.2 高斯投影改化

测距边在高斯投影面上长度比椭球体上大地线S要短，比测距边两端点在高斯投影面上的投影点连接所形成的线段D要长，即其在高斯投影下长度比m有如下关系：

(3)

高斯投影坐标正算公式为[7]：

(4)

将上式对l取偏导数得：

(5)

将式(5)代入式(2)并变换得：

(6)

用平面坐标(x，y)表示的长度比m计算公式为：

(7)

式中：Ym——测距边两端点横坐标平均值(m)；

R——测距边中点的平均曲率半径(m)；

△Y——测距边两端点近似横坐标的增量(m).

式(6)和式(7)是用大地坐标和平面坐标计算高斯投影变形长度比的计算公式，实际使用过程中由于直接获取的是平面坐标，所以普遍使用式(7)来进行高斯投影变形计算。

2.3 变形影响分析

对于城市轨道交通地面控制网边长而言，利用高程归化和高斯投影进行改正，前者使边长缩短，后者使边长伸长，存在两者抵偿的区域，即根据式(2)和式(7)，使：

(8)

考虑到测距边相对于地球半径是一个极小值，上式可写成：

(9)

因为城市地区高程变化，Ym仅是平均横坐标，地区总是有一个东西方向的宽度，因为完全抵偿是不可能的，如果不能完全抵偿而允许有一个残差VS，则其相对差数为：

(10)

根据《城市轨道交通工程测量规范》要求，精密导线边相对中误差为±1/60000，即使上式VS/D=±1/60000，设R=6 371 km，则：

(11)

上式Ym和H均以千米为单位，由此得抵偿区域的高差和相应横坐标区间的关系，如表1所示：

抵偿区域的高差和相应的横坐标区间 表1

由上表可以看出，对于一定的高程存在一定的抵偿区域，其东西宽度随着高程的增加而越来越窄，城市的区域往往不可能正在这一区域内。

根据我国现行规范要求，工程测量每千米边长经高程归化和高斯投影改化值不得超过 2.5 cm，即长度比m满足下式：

(12)

若仅考虑高程归化影响，以地球平均曲率半径 6 371 km计算，根据式(2)可知，当测距边两端平均高程与城市轨道交通工程测距平均投影面高程相差约 159 m时，每公里测距边长度变形超限；若仅考虑高斯投影变形影响，测距边长度变形值受纬度和距离中央子午线远近有关，由式(6)和式(7)可知，纬度越高，变形越小，距离中央子午线越远，变形越大。

综上分析，测距边长度变形分为高程归化和高斯投影变形两部分，两者在局部可以相互抵偿，变形值主要受三个因素影响，即测距边高程、纬度及与中央子午线的距离，当城市轨道交通工程线路在中央子午线附近时，可主要考虑高程归化的影响，当城市地形比较平坦，城市轨道交通工程采用的平均高程面与城市地势一致，可主要考虑高斯投影变形的影响。

以青岛市为例，中心建设城区平均纬度约为36°10′，虽然城区地势有高低起伏，但城市轨道交通工程平均地势接近平均海平面，平均投影面与平均海平面相一致，轨道交通建设测距边变形主要考虑高斯投影变形影响，距离中央子午线超过 45 km时，每公里边长变形值大于 2.5 cm。

3 工程应用

青岛市4号线是东西走向西路，整条线路位于中央子午线东端，其最东端距离中央子午线约 48.4 km；最西端中央子午线约 28.9 km。

图2 青岛地铁4号线走向及换乘线路示意图

高斯投影变形最大处位于沙子口站，每千米高斯投影变形值为：

本工程线路加权平均大地高与青岛市投影面高程相差约 8.2 m，高程归化影响每千米为：

满足规范不大于5 mm/km的变形要求。

高斯投影变形和高程归化影响最大处位于线路最东端沙子口站，该处距离120°中央子午线 48.4 km，设计轨顶大地高为 -3.3 m，每千米边长改正值为：

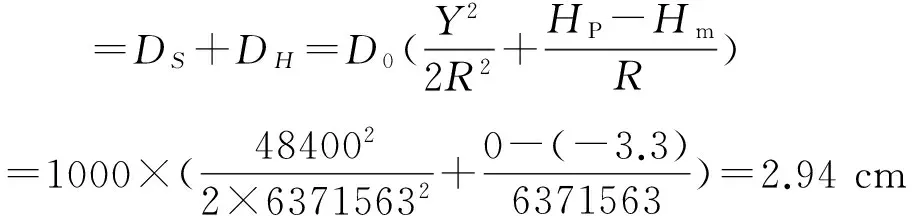
从以上分析可以看出，该项目边长改正最大值超出规范要求的 2.5 cm/km，从测区地理范围看，线路李宅路站往东约为 3.4 km的线路边长变形超过 2.5 cm/km，全线使用原有的中央子午线不符合规范要求，若在线路东段选取独立的中央子午线使得全线边长变形不超限，全线均使用换带后的独立坐标系，则线路西部与已建1号线、2号线、3号线及规划中多条线路换乘站坐标实际使用过程中将带来频繁的转换，容易出错，结合工程实际情况，本项目在西部采用青岛市原有坐标系统，东部重新选取中央子午线，采用独立坐标系，在李宅路站结合部提供两种成果以便于坐标转换。

4 总 结

(1)地铁建设过程中测距边长要经过高程归化和高斯投影改化两项改正，高程归化改正与测距边所在的高程与地铁线路平均高程面的高差有关，高差越大，改正越大，高斯投影改化与测距边距离中央子午线远近有关，具有中央子午线越远，改正越大。

(2)地铁测量测距边改正不得超过 2.5 cm/km，若超过该值，应结合地铁工程建设实际，充分考虑已建地铁线路与规划线路，在超过 2.5 cm/km区域应选取独立的中央子午线，并在两种坐标系结合部提供两种坐标系以便于坐标转换。

[1] 孔祥元，郭际明，刘宗泉等. 大地测量学基础[M]. 武汉：武汉大学出版社，2007.

[2] 王智，赵亚波. QDCORS在青岛地铁控制网中的应用研究[J]. 城市勘测，2016(4)：106～109.

[3] 梅熙. 高斯投影变形对高速铁路线路设计的影响[J]. 铁道工程学报，2010，27(10)：52～57.

[4] GB 50308-2008. 城市轨道交通工程测量规范[S].

[5] CJJ/T 8-2011. 城市测量规范[S].

[6] 赵俊生，刘雁春，王克平等. 关于高斯投影长度的探讨[J]. 海洋测绘，2007，27(3)：9～11.

[7] 尹玉廷，陈莉莉，康明等. 对高斯投影长度变形问题的简单探讨[J]. 测绘与空间地理信息，2010，33(5)：211～212.