最优化理论在椭球参数逆向求定中的应用

刘敏，王磊

(广州市城市规划勘测设计研究院，广东 广州 510060)

1 引 言

2008年我国正式启用的2000国家大地坐标系(CGCS2000)是经国务院批准使用的新一代国家大地坐标系。具有三维、高精度、动态等特点，能更好地满足各领域业务工作需要，更好地为经济建设、社会公众服务。统一采用2000坐标系，有利于各系统、部门之间资源和成果的共建共享，有利于促进各级基础地理信息数据成果的有效衔接，有利于推动地方“多规合一”、不动产统一登记等重大工作顺利开展。建立基于CGCS2000椭球体的地方坐标系，保持空间关系连续性，是大多数城市的优选策略。

许多城市独立坐标系统建立较早，椭球定义并不明确，或者是由于城市的扩展，经过多次扩展后的控制网投影自由度并不满足1/40000要求，也存在原有投影参数仍处于保密状态，为解决以上3类问题，本文提出一种基于最优化理论来逆向求定投影自由度，通过固定CGCS2000椭球体的扁率建立基于CGCS2000椭球体的地方坐标系。

图1 大地坐标与平面坐标转换

如图1所示，5个投影参数分别为，椭球参数(长轴a，扁率f，)、中央子午线l0、横坐标偏移量△Y、纵坐标偏移量△X。

一般情况下，是已知5个投影参数来求定一组大地坐标对应的平面坐标(反之亦然)。比如国家坐标系统，前两个用固定的椭球体区分，中央子午线采用标准经度(如3度带采用3*带号)。以上5个投影参数只要有1个与国家坐标系统不同，就可以称之为独立坐标系统。

本文的技术路线是：在已知一组同名点两种坐标情况下，逆向求定5个投影参数。

从投影平面坐标系互换到地理坐标系之间的五个投影参数的组合情况，理论上说有无数个合理实现两种坐标的转换(在规定的合理精度内)。

在众多的方案或组合中什么样的方案是最优的，最接近事实的，就需要引入最优化理论。

2 逆向求定投影参数的技术路线

地理坐标系统GCS中用经纬度来确定椭球面上的点位。投影坐标系始终基于地理坐标系，即：“投影坐标系=地理坐标系+投影算法函数”[1]。通用的GIS一般提供投影参数设置，GCS在建立地理信息平台或者数据信息共享上，比较有优势，但是在地方城市建设管理上，必须考虑与平面坐标系统衔接问题。

为从形式上让平面坐标与某个椭球体建立联系，从正形角度出发应该优先考虑固定椭球扁率，其次固定长轴，如图2所示。

3 最优化理论及MATLAB实现

最优化理论解决问题包含两个步骤：

(1)建立数学模型：用数学语言来描述最优化问题。模型中的数学关系式反映了最优化问题所要达到的目标和各种约束条件。

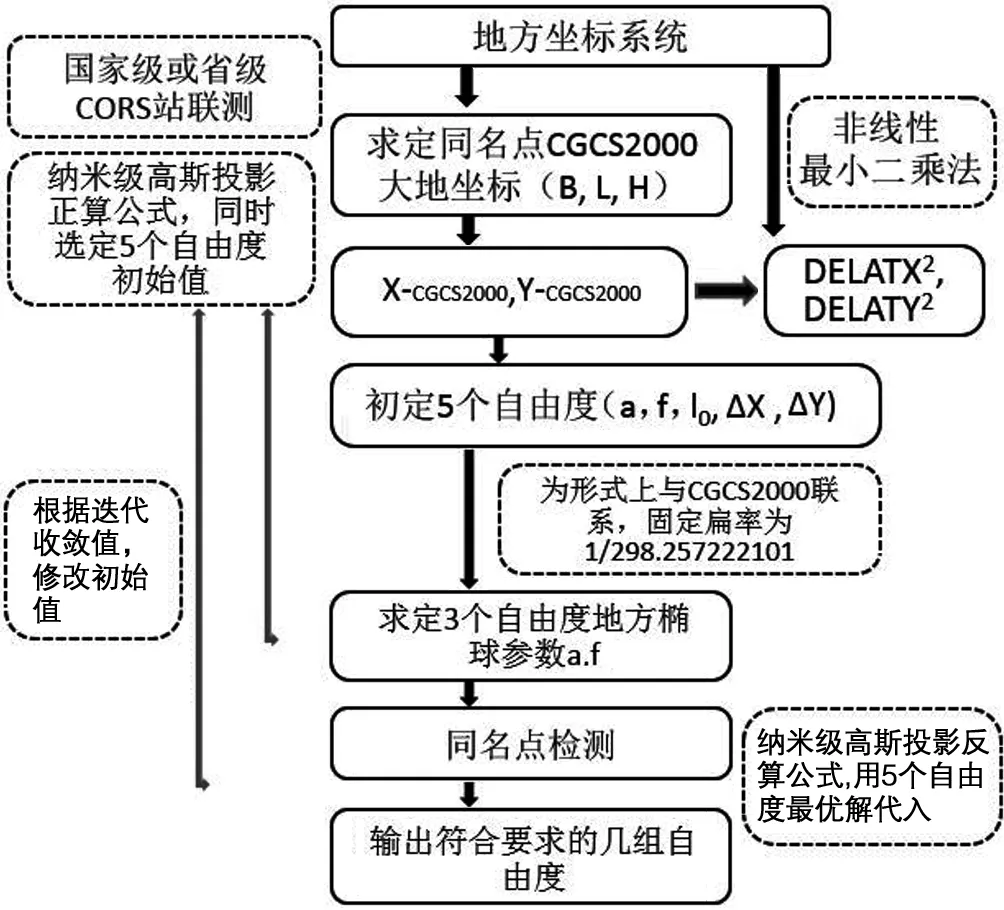
图2 投影自由度逆向求定的技术路线

(2)数学求解：数学模型建好以后，选择合理的最优化方法进行求解。

(1)首先对图像进行扫描，当扫到当前像素为1时选为种子，并给它赋予一个标签，然后按照四邻域准则，把与之相邻的所有值为1的像素点都压到栈内保存。

最优化理论常用的算法有两类，一类是搜索算法，另一类是迭代算法。

迭代算法是从参数的某一初始猜测值出发，然后产生一系列的参数点，如果这个参数序列收敛到使目标函数极小的参数点，那么对充分大的参数就可用来求解优化解。其中最小二乘法是最常用的方法，就是对由若干个函数的平方和构成的目标函数求极小值的问题。本文采用的就是通过迭代寻找min{sum[ Fun(x)2+Fun(y)2}的最小值。在同名点对中找出在符合最小二乘条件下的一组投影参数，并实现编程化处理。

通过编程工程和函数比选，本文采用MATLAB优化工具箱提供的Lsqnonlin函数来解决非线性最小二乘法问题。其算法就是采用Trust-region-reflective(信赖域反射算法)和Levenberg-marquardt(加权信赖域算法)。

信赖域法是从给定的初始解出发，通过逐步迭代，不断改进，直到获得最优解为止。具有收敛性较好、可靠性高，有效性强等特点。Lsqnonlin函数处理的是非线性最小均方差问题。函数从初值开始，最后到找满足函数Fun(x)均方误差和最小的x值返回。选定合适的初值可以保障非线性最小二乘法收敛速度加快。

4 高精度Gauss-Krueger公式

4.1 传统的Gauss-Krueger公式

Gauss-Krueger投影是一种等角横轴切椭圆柱投影，在投影面上，中央子午线和赤道的投影都是直线，其他子午线和平行线是复杂曲线。传统投影公式是利用黎曼柯西方程给出的实数形经差的幂级数函数展开。该公式适用范围比较窄(经差在4°～6°)在反算过程中的不准确性表现明显，经MATLAB程序测试，该公式正反算精度不高，在非线性最小二乘过程中收敛值偏大，不适用于本文要求。但这个公式在国内外教科书被广泛采用。

4.2 Karney-Krueger公式

Karney-Krueger按精度也分两类公式：

第一类称为扩展的Krueger(1912年)公式。该公式是利用计算机代数系统Maxima扩展了Krueger(1912年)的原始系列(第三扁率n的4阶)至8阶甚至30阶。在第三扁率n高阶至6时，距离中央子午线 4 200 km，正反算的精度达到优于 5 nm[6]。该公式精度高，投影范围广(经差可以扩展至75°)，同时适用于高纬度地区。

扩展的Krueger公式，原理是利用等量纬度与归化纬度关系，把等量纬度和经差作为变量拓展至复数域。再借助双曲正弦函数及其与三角函数的关系，把投影的复变函数表达式拆为实虚分离的实数形式。

推导过程大致为可以用图3表达：

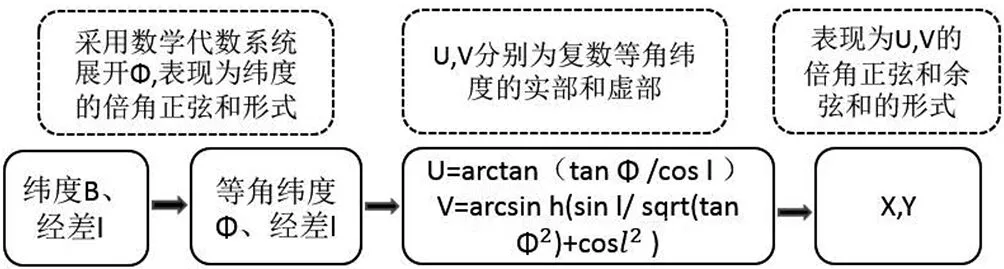
图3 Karney-Krueger第一类公式原理

第二类是采用雅克比椭球函数进行椭球积分，利用计算机代数系统Maxima可以达到任意精度。

该公式精度可以达到任意精度(在计算机内存允许的范围内)，投影范围更广(适应全椭球体)。

本文采用的是扩展至6阶的Karney-Krueger第一类公式进行高精度正反算。采用高精度的高斯投影正反算公式是本文逆向求定投影参数的关键所在。

5 实例验证

5.1 迭代初值的选择

根据公开文献报道，广州市坐标系统采用克拉索夫斯基椭球(1954年北京坐标系)为基础，并采用不同于国家标准经线(114°)作为中央子午线，并对横坐标偏移量△Y、纵坐标偏移量△Y同时进行了偏移，根据本文对投影自由度的定义，该市坐标系是典型的非国家坐标系。

椭球体长轴a，扁率f可以选用1975IAG椭球或CGCS2000椭球作为初始值带入。中央子午线以城市中心经度113.50°为初值；横坐标偏移量△Y、纵坐标偏移量△X选用城市中心同名点横纵差值代入，如图4所示。

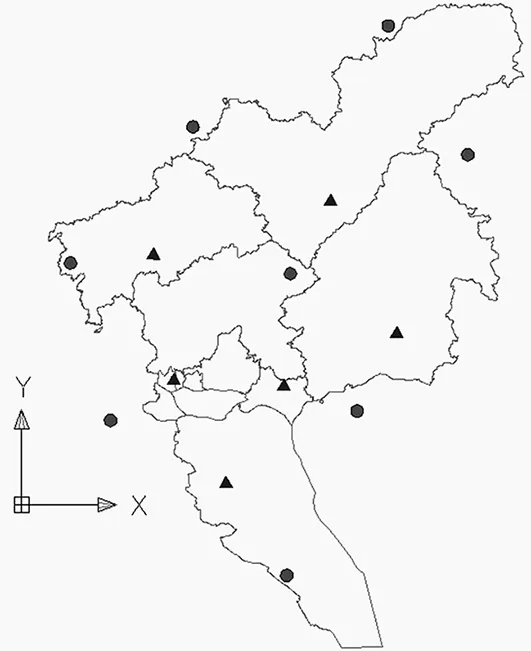
图4 起算点与检测点分布示意图

5.2 投影自由度迭代技术

根据本文技术路线，图3中8个起算点和6个检测点同时具有CGCS2000坐标和广州市坐标系统[1]。

第一步，根据技术路线，采用MATLAB编写程序，分三个函数执行。具体代码可联系本文作者或参见相关文献[4]。其中纳米级高斯正反算公式采用Karney-Krueger 第三椭球扁率阶数6计算。得出以下5个投影自由度：

椭球体长轴a，椭球体扁率f、中央子午线l0、横坐标偏移量△Y、纵坐标偏移量△Y；(因多方面原因，以下部分数据有所省略)

6378126.*** ；1/298.255456291；113.17**；411*3.***；-25296*5.***

第二步，为形式上建立独立坐标与CGCS2000之间的关系，可以固定扁率为CGCS2000扁率，其他4个自由度分别为：

6378126.5**；1/298.257222101；113.17**；411*3.*** ；-25296*5.***；可以从第一步和第二步得出的椭球体长轴a变化、坐标偏移量△Y、纵坐标偏移量△Y均在分米级上，说明整个非线性最小二乘的优化解是收敛的。

第三步，为固化与CGCS2000椭球体的长轴关系可以约定在原有椭球长轴6378137修改至整数长度，再进行一次非线性最小二乘。

第四步，将以上各步骤得出的5个投影自由度代入纳米级高斯反算公式，与已知点进行比较，坐标偏差均小于 2 mm，证明在全市域以上几套投影自由均是满足要求的，如要在形式上与CGCS2000建立联系，可以分别采用第二步以后的各组投影自由度。

6 结 论

随着计算机技术的发展，在城乡规划管理中直接(后台数据库或间接使用)采用CGCS2000大地坐标(BLH)是历史发展的必然趋势。

许多独立坐标无确切的数学模型，一般四参数或七参数与CGCS2000建立联系，本文通过逆向求定投影参数，建立地方坐标与CGCS2000简单的高斯投影关系，有着积极的现实意义，也为大地坐标作为地理信息系统后台数据库奠定了数学基础。

[1] 刘敏. 城市CORS站转换到CGCS2000的技术研究[J]. 城市勘测，2013(2)：113～115.

[2] Karney，C.F.F. (2011)，'Transverse Mercator projection with an accuracy of a few nanometres'，Journal of Geodesy.

[3] 施一民. 现代大地控制测量[M]. 北京：测绘出版社，2003，220～225.

[4] 刘万华，叶水全. 构建独立坐标系与CGCS2000 坐标系转换关系的研究[J]. 测绘与空间地理信息，2016，39(1) ：216～218.

[5] 边少锋，刘强，李忠美. 不分带的高斯投影实数公式[J]. 测绘通报，2016，1(1) ：6～9.

[6] Lee，L.P. Conformal projections based on Jacobian elliptic functions，Cartographica[J]. 1976，13，128～129.

[7] Yang，Q.，Snyder，J.P. and Tobler，W.，Map Projection Transformation [M]. 2000，100-108，Taylor & Francis，London.

[8] Deakin，R.E. and Hunter，M.N. Geometric Geodesy Part B，School of Mathematical and Geospatial Sciences[J]. 2010，28～30.

[9] 刘强，边少锋，李忠美. 球面高斯投影及其变形的闭合公式[J]. 海军工程大学学报，2015，27(1)：46～48.