隐高斯树的分层合成——一种基于信息论解决合成问题的方法

Ali Moharrer 魏双庆 骆 源

1路易斯安那州立大学巴吞鲁日70803

2上海交通大学上海200240

3上海交大-中国联通-广视通达大数据联合实验室上海200240

引言

本文基于高斯分布，通过提出高效合成概念，研究“具有规定联合密度的随机向量产生机制”。粗略地说，这种高效性可以通过寻找表达随机向量整体依赖性的、最紧凑的公共随机源实现。如果我们能从随机变量样本提取出这些公共随机性，剩下的样本就是随机噪声。本文所提出的方法不但可以揭示数据隐含的内部联系，而且适用于在机器学习领域中产生仿真数据。最近的几篇使用相关度量来解决某些特定的检测和估计问题的论文[1-3]，便是旨在找到这样的公共随机源。此外，由文献[4]、[5]表明，通过诸如变分自编码器(VAEs)和神经网络(Neural Networks)等机器学习工具及其信息瓶颈分析方法来学习随机系统中最紧凑的参数，可得到更好的泛化效果。

在本文中，我们的目标是提出一个直观可操作的配置方法来合成某些类型的联合密度。总体思路是对统计数据中的隐藏公共随机性进行建模和模拟，然后依次加入独立噪声元素来模拟整体数据。具体来说，可以通过将适当数量的随机比特输入随机信道来实现这一模型，其输出向量的经验统计在给定衡量标准下满足期望值。本文的工作在数据合成领域中有广泛的应用：1)数据匿名化，例如可以保护包含了敏感个人信息的真实数据集的隐秘性和保密性[6]；2)数据集扩充，例如可以用于扩展训练特定机器学习算法的数据集[7]。在这些用途中，数据的特定统计学特征被捕捉并被用于合成新的数据。

我们旨在为如下情况提供解决方案：由规定的输出统计数据引出一个(隐)高斯树，假定其联合分布为高斯分布，而且隐变量和观测变量的条件统计独立关系具有稀疏的树结构。由于模型中出现的条件独立关系与协方差矩阵的逆矩阵中的零点直接对应，尤其是其稀疏的结构以及现有的拓扑学习的高效算法[8-9]，使高斯图模型受到广泛关注，并在社交网络、生物学、经济学中有不同的用途[10-11]。

2 相关工作

要解决合成方案中的高效性问题，Han和Verdu[12]引入了给定信道可分解性的概念，该概念被定义为产生输出数据所需的最小随机性，并用合成密度和规定密度之间的总变分距离(Total Variation Distance)度量。在文献[13]、[14]中，作者的目标是定义n个相关随机变量的公共信息，以进一步解决这种问题。虽然他们将以前的工作从双变量的情况推广到n个随机变量，但是他们仍然采用与Wyner[15]一样的方案，即用单一源来定义这样的公共随机性。这对我们的仿真方案来说是一种特殊的情况，其中所有的变量都通过一个公共变量相互关联，我们将这种结构定义为星型树。在文献[16]中，作者将两个联合高斯向量之间的公共信息描述为奇异值的函数，其中奇异值与两个高斯随机向量之间的协方差矩阵有关，然而，他们仍然是将随机向量分成两组，这与Wyner的论文[15]中的双变量情况类似。

3 系统模型

以上介绍的相关研究仅仅考虑了两组随机向量，在本节中，我们提出一种新的合成方式，不再只考虑通过一个输入向量来合成数据，而是引入了代表相关系数符号信息的伯努利变量B作为另一种随机源，提高了合成效率。

在隐高斯树中，我们将处理两组变量。X={X1,X2,…Xn}表示高斯树上n个观测变量，其协方差矩阵∑X已给出。向量集Y={Y1,Y2,…Yn}对我们来说是隐藏的，是需要被估计的。值得注意的是，在使用∑X生成隐高斯树时，需要满足文献[11]中的某些条件。已有一些文献，如文献[10]、[17]提出了高效的算法来推算高斯树的参数。事实上，Choi等人提出了一种新的递归组合(RG)算法及其改进版本，即Chow-Liu RG(CLRG)算法，这种算法能恢复出一棵结构和风险与原先一致的高斯树，这支持了算法的正确性。他们引入了树的度量，即两两相关值的绝对值的负对数，来运行算法。在本文中，我们假设使用上述算法之一来获得隐高斯树的参数和结构信息。

在这种合成问题中，我们主要关注的是合成高斯树所需输入的公共随机比特数量的高效性。这一高效性表征为定义适当的随机序列以及包含那些序列的随机容器(我们分别定义为随机码字和码本)。我们用输入的码率来定义合成系统的复杂度，因为极小化这一码率会减少生成输出数据所需的公共随机比特位数。为了让公共随机源尽可能紧凑，我们从统计数据中提取尽可能多的独立随机性。特别的，由于隐高斯树具有固有的符号奇异性，我们认为这种不确定性可以进一步帮助我们降低高斯树的合成率。为了阐明这一点，考虑下面的例子。

例1：考虑图1所示的高斯树，它由X1，X2，X3，X4四个观测变量组成，通过两个隐藏节点Y1(1)和互相连接。定义为输入和输出X1之间的相关值(边权)，类似地，定义其他相关值。定义符号Bj(1)∈{-1,1}，j∈[1,2]作为第j个输入值对应的二元变量，我们将会看到它反映了两两相关值的符号信息。对于图1展示的树，可以假设符号，而对应，其中i∈[1,2]or i∈[3,4]是使用某种推断算法，比如RG算法[10]所得到的相关值。同样的，定义符号。容易看出恢复相关值推导出相同的协方差矩阵∑X，表明了在这个高斯树中的符号奇异点问题。尤其是，对每个两两相关系数，k＜ι∈[1,2,3,4]，如果xk，xι有相同的父节点，可以得到，其中第二个等式是因为不管符号值是多少，等于1。现在，根据符号在{-1,1}中的取值，可以得到。并且，我们没有办法用目前所观察到的联合分布信息来区分这两种情况。相似的，如果xk、xι连接不同的输入结点，则，第二个等式成立是因为。同样的，无法仅根据输出的相关值恢复符号信息。

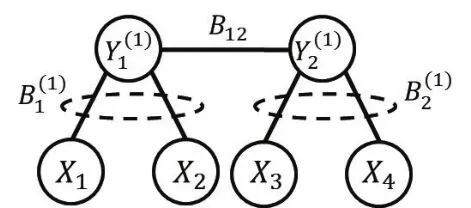
图1 一个以Y1(1)，Y1(2)为隐藏节点的简单高斯树

这证明了这样的符号奇异点可以被视为另一种随机噪声源，它可以进一步帮助我们降低合成高斯树所需的码率。事实上，我们可以将图1中的高斯树想象成一个通信信道，来自的信息流通过四个信道，伴随独立的加性高斯噪声变量，从而生成输出。我们引入以为分布参数的二元伯努利符号随机变量，反映了两两相关系数的符号信息。事实上，我们可以将输入到输出定义为以下的仿射变换。

我们的目标是描述可达到/可实现的码率范围，并通过一个合成方案来生成密度为的所有高斯树，其中b(1)可取不同值，合成的混合密度与真实混合高斯树密度要求很难用总变分度量区分。为了达到我们的目的，首先生成许多采样序列和来形成码本。码本的大小为，其中和是码率，这和符号以及隐藏节点码字有关。每一次生成输出序列时，我们首先任意的选择一个符号和隐藏节点码字，然后使用(1)中定义的合成信道来获得一个特定的输出序列XN。我们的目的是通过生成序列的统计特性，即趋近于期望的统计数据，来形成码率的下界。具体来说，我们定义下界为，其中是输出X和输入向量之间的互信息量。这对应于在高斯树假设下求解最小可达速率。等价的，我们寻找的最优值来最大化由描述的可达速率范围。为了阐明这种分层设计是如何影响统计数据的模拟的，考虑下面这个例子。

例2：在这个例子中，我们只证明这种分层方法确实能够生成目标高斯密度的样本。因此，为了简单起见，我们不考虑例子中的符号变量。高斯树此时具有如图2所示的叉形结构。

图2 以Y1(1)为隐藏节点的简单高斯树

这是一个有高斯源Y(1)和B(1)符号输入并以向量X=[X1,X2,X3]为输出的隐星形拓扑结构，可以按照下式建模。方便起见，我们将符号变量设为B(1)=1。假设协方差矩阵∑x已给出，其对角线上值为，非对角线上的值都相等且为，文献[18]证明了在这种情况下系数αi可以被唯一确定，在这个例子中它们都相等且。噪声方差都被确定且均等于。粗略地说，我们首先生成一个样本Yi和另一个随机加性噪声样本Zi，根据(2)得到。前文指出当速率时可达，这里互信息可以通过来计算[19]，其中|.|表示行列式，在本例中，。

正如我们讨论的，随着维度N的增加，样本数量指数增加并接近目标高斯密度，文献[20]也证明了这一点，码本尺寸以速率增加。

例1和例2展示了我们合成方法的总体思路。在这里，我们给出隐高斯树在一般情况下的严格问题描述和操作设置。

1)使用总相关度量而不是KL散度来显示收敛性。

2)定义了回溯技术来合成整个混合高斯树而不仅仅是观测向量X。特别的，我们想要强调多变量合成概念，定义一个具有一定依赖性结构的随机向量Y来表征公共随机性并生成公共随机位，而不是仅仅引入一个变量Y。我们提供了一种分层合成算法，配以相应的可达区域，来合成能够导出高斯树的分布。在文献[17]中这样的情况一般使用受约束的凸优化问题来定义，文献[3]证明了这种一般化假设的好处。事实上，针对盲源分离问题，Steeg等人使用了一种基于多层公共变量的新方法，并证明了他们提出的方法优于之前的算法。与文献[3]、[17]类似，我们也考虑了多变量情况，但不同的是，我们所感兴趣的是表征可实现的速率，从而合成满足特定类别的隐高斯分布，即隐高斯树。值得指出的是，本文的结果在假定的结构化合成框架下给出。因此，虽然我们通过定义一个最优化问题，证明了提出的方法在建模和码率上都是高效的，但我们并没有反过来对该方案和速率区域的最优性进行讨论。

3)在前文的例子中，将符号变量设为特殊值。在接下来的内容中，我们将展示如何利用符号奇异性，将符号变量作为另一个独立的随机源来合成受符号模糊性影响的高斯树。由于相关符号不确定性带来的等效噪声效应，我们实际需要的用于合成隐藏连续变量的比特数也随之减少。

例2通过研究一个具体案例，我们提供操作设置和可实现速率的区域，从而合成服从PXY的树形结构的样本。这里，向读者推荐文献[18]，来更全面地研究一般高斯树结构。我们在更一般化的情形中处理多分层隐高斯树。图3展示了一般的合成方案，在每一层i，定义为合成的输入向量。

例3：考虑图4所示的情况，其中高斯树具有两层输入。我们可以计算第一层中的两两协方差，其中。输入向量对于每个给定的都符合高斯分布。因此，可以将码本C分成部分，每一部分都服从以为协方差的特定高斯密度。

图4 两层高斯树

下面阐述在这种情况下连续码本的生成方法。首先，需要从顶层到第一层生成每一层的码本。符号码本是预先生成的，且仅仅与符合伯努利分布的符号向量有关。每个符号码字是一个向量序列，其元素从{-1，1}中选择。我们也可以用混合高斯码字来生成顶层码本每个时隙中每个码字由所有可能值组成。每一个设定都表征了一个顶层隐变量的特定高斯分布，所需码字的数量为。我们知道要使用中的码字来生成第二层的码字，需先从中随机选择码字，然后基于选择的符号码字，生成序列并送入信道中。符号向量包含了个符号变量，因此有个不同信道。所以，我们将选择的序列通过8个不同信道来产生中的一个码字。注意，这种方式产生的码字实际上是高斯向量的集合，每一个都对应于一个特殊的符号向量。将这一过程重复次，产生合成下一层所需的全部码字。图5展示了前文描述的合成过程。为了生成一个输出序列，我们需要做的就是随机地从选择码字。然后根据每个时隙的符号实现，使用对应的信道来生成输出序列。

图5 合成图4所示高斯树的码本生成方案

因此，为了合成足够接近真实高斯树分布的数据，需要首先生成顶层码本和符号码本，注意合成方案是需要独立高斯噪声作为给定的随机源。

图5中给出的自顶向下方案，为每一层生成适当的码本。为了选择合适的码字，需要保持追溯输入输出的关系。考虑每层的输出，我们回溯生成这种输出对应的输入码字。举例来说，考虑与图4中相同的高斯树，为了生成输出序列XN，我们从对应的码本中随机的选择两个码字。符号码字决定了该输出对应的信道，因此在该输入码字和生成的输出之间有着对应关系。类似的，是顶层输入的输出，由随机选择的码字生成。图6展示了由图4所示的双层隐高斯树的合成方案。

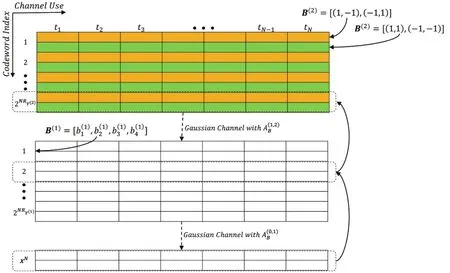
图6 图4所示高斯树的合成方法

在图6中，码本中不同的颜色对应了不同的符号实现。举例来说，我们知道对应顶层符号输入可以有个不同的符号实现，因此对应的码本中有两种不同的颜色。同样，码本中每个小格包含一个样本向量，是因为每层通常包含不止一个变量。比如顶层码本的每个小格包含两个高斯样本，对应于，其中。在生成方法中，首先随机地从中挑选序列并形成，然后找到第一层中对应的输入码字。接着，被选择的码字通过给定的高斯信道生成输出向量。这种情况下，样本序列(如图6)是值得注意的是，每层码字都携带了在码本生成步骤中被确定的对应符号信息。

4 仿真结果

图7展示了2 000个合成样本的一维经验密度和不同维度N下的理论高斯密度的比较。特别的，图7左侧的图展示了真实输出密度和样本归一化直方图之间的比较；右侧的图比较了合成输出样本的密度与真实输出密度。可以看出，随着N的增加，输入的可选序列也随之增加，期望的高斯密度被更好地拟合，结果就是我们更加接近要被模拟的高斯密度。

图7 合成数据的比较

特别的，我们可以计算期望高斯密度P(X)和合成密度P(X)之间的KL距离，并观察到KL距离随N的变化规律。计算方法定义如下。

同样的，在之前的例子中我们指出，由于高斯树的符号奇异性，我们可以暂且忽略符号变量，即取，并得到与取 统计学上相同的结果。我们可以看到B的选择不影响合成方案的整体表现。同时，随着维度N的增加，尽管KL距离整体上减少了，但并非单调递减。这是因为合成方案的随机性，也就是说，一些样本给出了更接近真实高斯密度的结果。在文献[20]中，这些样本被称作精选码字，这种影响在高维度中逐渐消退，使KL距离变成了随N单调递减的函数。如图8所示。

图8 当，真实数据与合成数据之间的KL距离

5 总结

本文基于高斯分布研究“具有规定联合密度的随机向量产生机制”。与以往的合成方案相比较，我们增加了代表模糊性的伯努利符号环节，使得模型能够利用更广泛的混合高斯分布随机向量。这为揭示数据隐含的内部联系，以及在机器学习领域产生仿真数据，提供了更宽广的应用场景和模型理论。

[1]STEEG G V.Unsupervised learning via total correlation explanation[C]//Twenty-sixth International Joint Conference on Artificial Intelligence,2017:5151-5155

[2]STEEG G V,GALSTYAN A.Low complexity gaussian latent factor models and a blessing of dimensionality[Z].arXiv preprint arXiv:1706.03353,2017

[3]STEEG G V,GAO S,REING K,et al.Sifting common information from many variables[C]//Twenty-sixth International Joint Conference on Artificial Intelligence,2016:2885-2892

[4]ACHILLE A,SOATTO S.Information dropout:Learning optimal representations through noisy computation[Z].arXiv preprint arXiv:1611.01353,2016

[5]SHWARTZ-ZIV R,TISHBY N.Opening the black box of deep neural networks via information[Z].arXiv preprint arXiv:1703.00810,2017

[6]SORIA-COMAS J,DOMINGO-FERRER J.A nonparametric model for accurate and provably private synthetic data sets[C]//The 12th International Conference on Availability,Reliability and Security.ACM,2017:3

[7]DEVRIES T,TAYLOR G W.Dataset augmentation in feature space[Z].arXiv preprint arXiv:1702.05538,2017

[8]CHOI M J,TAN V Y,ANANDKUMAR A.Learning latent tree graphical models[J].The Journal of Machine Learning Research,2011,12:1771–1812

[9]SHIERS N,ZWIERNIK P,ASTON J A.The correlation space of gaussian latent tree models[J].Biometrika,2016,103(3):531–545

[10]DOBRA A,EICHER T S,LENKOSKI A.Modeling uncertainty in macroeconomic growth determinants using gaussian graphical models[J].Statistical Methodology,2010,7(3): 292–306

[11]MOURAD R,SINOQUET C,ZHANG N L.A survey on latent tree models and applications[J].J.Artif.Intell.Res.(JAIR),2013,47:157–203

[12]Han T S,Verd U S.Approximation theory of output statistics[J].IEEE Transactions on Information Theory,1993,39(3):752–772

[13]Yang P,Chen B.Wyner's common information in gaussian channels[C]//IEEE International Symposium on Information Theory(ISIT),2014:3112–3116

[14]Xu G,Liu W,Chen B.A lossy source coding interpretation of wyner’s common information[J].IEEE Transactions on Information Theory,2016,62(2):754–768

[15]Wyner A D.The common information of two dependent random variables[J].IEEE Transactions onInformation Theory,1975,21(2):163–179

[16]Satpathy S,Cuff P.Gaussian secure source coding and wyner's common information[Z].arXiv preprint arXiv:1506.00193,2015

[17]GASTPAR M C.Total correlation of gaussian vector sources on the gray–wyner network[C]//54th Annual Allerton Conference on Communication,Control and Computing(Allerton),2016

[18]MOHARRER A.Information theoretic study of gaussian graphical models and their applications[D].Louisiana State University,2017

[19]MOHARRER A,WEI S.Algebraic properties of solutions to common information of Gaussian vectors under sparse graphical constraints[C]//55th Annual Allerton Conference on Communication,Control and Computing(Allerton).IEEE,2017

[20]CUFF P.Soft covering with high probability[C]//2016 IEEE International Symposium on Information Theory,Barcelona,Spain,2016:2963–2967