集成学习之随机森林算法综述

王奕森 夏树涛

清华大学深圳研究生院/计算机科学与技术系深圳518055

引言

分类和回归问题几乎涵盖了现实生活中所有的数据分析的情况，两者的区别主要在于我们关心的预测值是离散的还是连续的。比如，预测明天下雨不下雨的问题就是一个分类问题，因为预测结果只有两个值：下雨和不下雨(离散的)；预测中国未来的国民生产总值(GDP)就是一个回归问题，因为预测结果是一个连续的数值。在一些情况下，通过把连续值进行离散化，回归问题可以转化为分类问题，因此，我们在这篇文章中将主要研究分类问题。传统的分类的机器学习算法有很多[1]，比如决策树算法(Decision Tree)[2-4]、支持向量机算法(Support Vector Machine)[5]等。这些算法都是单个分类器，他们有性能提升的瓶颈以及过拟合的问题；因此，集成多个分类器来提高预测性能的方法应运而生，这就是集成学习算法(Ensemble Learning)[6]。Bagging[7](并行)和Boosting[8](串行)是两种常见的集成学习方法，这两者的区别在于集成的方式是并行还是串行。随机森林算法(Random Forests)[9]是Bagging集成方法里最具有代表性的一个算法，这也是本文重点总结的算法。

随机森林是基于决策树的一种集成学习算法。决策树是广泛应用的一种树状分类器，在树的每个节点通过选择最优的分裂特征不停地进行分类，直到达到建树的停止条件，比如叶节点里的数据都是同一个类别的。当输入待分类样本时，决策树确定一条由根节点到叶节点的唯一路径，该路径叶节点的类别就是待分类样本的所属类别。决策树是一种简单且快速的非参数分类方法，一般情况下，它有很好的准确率，然而当数据复杂时，决策树有性能提升的瓶颈。随机森林是2001年由Leo Breiman将Bagging集成学习理论[10]与随机子空间方法[11]相结合，提出的一种机器学习算法。随机森林是以决策树为基分类器的一个集成学习模型，如图1所示，它包含多个由Bagging集成学习技术训练得到的决策树，当输入待分类的样本时，最终的分类结果由单个决策树的输出结果投票决定。随机森林解决了决策树性能瓶颈的问题，对噪声和异常值有较好的容忍性，对高维数据分类问题具有良好的可扩展性和并行性。此外，随机森林是由数据驱动的一种非参数分类方法，只需通过对给定样本的学习训练分类规则，并不需要先验知识。

图1 随机森林算法图解(整体图)

在Breiman提出随机森林算法之后，由于其良好的性能表现，该算法被广泛应用到诸如生物信息领域对基因序列的分类和回归[12-13]、经济金融领域对客户信用的分析及反欺诈[14-15]、计算机视觉领域对人体的监测与跟踪、手势识别、动作识别、人脸识别、性别识别和行为与事件识别[16-17]，语音领域的语音识别与语音合成[18]、数据挖掘领域的异常检测、度量学习[19-20]等实际领域。总结来看，在随机森林研究领域，目前有三个方面的研究热点。1)随机森林算法在性能改进方面的研究，特别是在高维数据情况下，随机森林算法的性能还有待提高。2)随机森林算法在理论性质方面的研究，相比于随机森林在应用方面的大量研究，其理论研究明显滞后。随机森林算法的一致性等还没有被完全证明。3)同样作为分层算法，随机森林和目前最热的深度学习有怎样的区别和联系，以及如何结合才能产生更好的算法，也是目前研究的一个热点。本文将从以上三个方面对随机森林算法领域的研究进行总结，期望能对新入行的读者起到引导作用，及已经是该领域的学者产生启发作用。

1 随机森林算法简介

1.1 决策树

决策树是一个无参有监督的机器学习算法。Quinlan提出了ID3决策树算法[2]，Breiman等人提出了CART决策树算法[4]，1993年Quinlan又提出了C4.5决策树算法[3]，Wang和Xia又于2016年提出了Tsallis决策树算法[21]。一般而言，决策树的建树最常见的是自下而上的方式。一个给定的数据集被分裂特征分成左和右子集，然后通过一个评价标准来选择使平均不确定性降低最高的分裂方式，将数据集相应地划分为两个子节点，并通过使该节点成为两个新创建的子节点的父节点来建树。整个建树过程是递归迭代进行的，直到达到停止条件，例如达到最大树深度或最小叶尺寸。

决策树的一个关键问题是节点分裂特征的选择。至于分裂标准，一系列论文已经分析了它的重要性[22-23]。他们证明了不同的分裂标准对决策树的泛化误差有很大的影响；因此，根据不同的划分标准，提出了大量的决策树算法。例如，ID3算法基于香农熵；C4.5算法基于增益比；而CART算法基于Gini不纯度。然而，在这些算法中，没有一个算法总能在各种数据集上得到最好的结果。实际上，这反映了这种分类标准缺乏对数据集适应性的一个缺点。因此，已经有学者提出自适应熵估计的替代方法[24-25]，但是它们的统计熵估计过于复杂，使决策树的简单性和可理解性丧失。最近，Tsallis熵分裂准则被提出来统一通用分裂准则[21]，即统一了香农熵、增益比和Gini不纯度。

决策树不需要先验知识，相比神经网络等方法更容易解释，但是由于决策树在递归的过程中，可能会过度分割样本空间，最终建立的决策树过于复杂，导致过拟合的问题，使得分类精度降低。为避免过拟合问题，需要对决策树进行剪枝[26]，根据剪枝顺序不同，有事先剪枝方法和事后剪枝方法，但都会增加算法的复杂性。

1.2 随机森林

决策树是单个分类器，通过上述分析，可以看出其有性能提升的瓶颈。集成学习是将单个分类器聚集起来，通过对每个基本分类器的分类结果进行组合，来决定待分类样本的归属类别。集成学习比单个分类器有更好的分类性能，可以有效地提高学习系统的泛化能力。

假定给定的数据集为D={Xi,Yi}，Xi∈RK，Yi∈{1,2,…,C}，随机森林是在此数据集上以M个决策树{g(D,θm),m=1,2,…,M}为基分类器，进行集成学习后得到的一个组合分类器。当输入待分类样本时，随机森林输出的分类结果由每个决策树的分类结果进行多数投票决定。随机森林里有两个重要的随机化，如图2所示。

图2 随机森林算法流程图(细节图)

1)样本Bagging：从原样本集D中通过bootstrap有放回地随机抽取M个与原样本集同样大小的训练样本集Dm，然后据此构建一个对应的决策树。

2)特征的随机子空间：在对决策树每个节点进行分裂时，从全部K个特征中均匀随机抽取一个特征子集(通常取log2K)，然后从这个子集中选择一个最优分裂特征来建树。

由于构建每个决策树时，随机抽取训练样本集和特征子集的过程都是独立的，且总体都是一样的，因此，{θm,m=1,2,…,M}是一个独立同分布的随机变量序列。由于各个决策树的训练相互独立，因此，随机森林的训练可以通过并行处理来实现，该性质有效地保证了随机森林算法的效率和可拓展性。

2 随机森林算法的性能提升

根据Breiman给出的随机森林泛化误差的上界[9]：

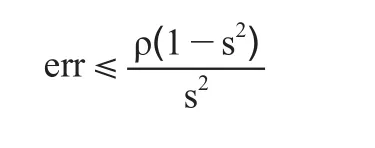
我们可以看出随机森林的泛化误差界与单个决策树的分类强度s成负相关，与决策树之间的相关性成正相关，即分类强度越大，相关性越小，则泛化误差界越小，随机森林分类准确度越高。这也启发我们，对随机森林模型进行改进时，可以从两方面着手：一是提高单棵决策树的分类强度s，二是降低决策树之间的相关性。随机森林在高维数据上的表现并没有它在中低维数据上的表现好，因此，有一系列的研究工作针对随机森林在高维数据下的性能提升。

旋转森林算法(Rotation Forests)[27]引入了主成分分析(Principal Component Analysis，PCA)[28]的特征变换，相当于把数据集上的原始特征旋转到了主成分所在的方向，进而再进行后续的基于特征子空间的随机森林的构建，这里的集成是建立在整个数据集的所有主成分之上的。此外，还有另外一些类似的方法应用到随机森林里，比如，使用前S个主成分构建第一棵决策树，接着用后续的S个主成分构建第二棵决策树，这样依次下去[29]。但是，这种方法会导致比较靠后的决策树是在包含比较少的信息的特征子空间上构建的，会降低决策树的性能，进而伤害集成之后的随机森林的性能。此外，还有一些文献把PCA作为特征提取和降维的预处理方法，这些算法只保留了很少的一些较大值的主成分，这导致他们有一个缺点就是由于只有少数主成分被保留，那些对应于小主成分值但是却包含最相关的判别信息的特征可能被丢弃[30]。

此外，还有一些从特征子空间选择的角度入手来提升随机森林性能的。均匀随机地选取部分特征构成特征子空间在高维数据的情况下，会导致随机森林的性能下降，这是因为随机选择的特征子空间可能包含很少或者没有信息量的特征，这会导致依赖于此特征子空间的决策树的性能下降，进而影响集成的随机森林的性能[31]；因此，有一系列的文献采取了分层采样的方法来解决这个问题，他们主要关注于如何把特征根据包含信息的多少分开，然后对不同信息量的特征采取分层采样的方式构成特征子空间。分层随机森林(Stratified Random Forests)[32]采用Fisher判别投影得到的权重把特征分为两部分，即强信息特征和弱信息特征。子空间选择随机森林(Subspace Selection Random Forests)[33]应用一个统计准则把特征分为三部分。首先，应用p-value来衡量特征的重要性，把特征分为信息特征和非信息特征。其次，应用卡方统计量进一步把信息特征分为高信息特征和信息特征两部分。基于主成分分析的分层采样随机森林(Principal Component Analysis and Stratified Sampling based Random Forests)[34]提出了一种根据PCA输出的结果把特征划分为信息特征和非信息特征的准则的一种方法。此外，还有一种对特征进行加权的方式来取代分层采样[35]。他们首先计算特征与类别之间的相关性，并把这种相关性认为是该特征在特征子空间中被选到的概率，但是这种方式可能会引入更多强相关的决策树，因为那些具有很大权重的特征很可能被重复多次地选到。

3 随机森林算法的理论研究

与随机森林在许多实际应用中展现出的非常有吸引力的实际性能相比，它们的理论性能还没有完全建立，仍然是积极研究的课题。对于一个学习算法来说，一致性是最基本的理论性质，因为它确保了随着数据增长到无限大而算法能收敛到最优解。一致性的定义如下：对于分类问题，给定训练集D，对于一个(X,Y)的分布，我们说随机森林分类器g具有一致性，如果

这里的L*代表贝叶斯风险，也就是(X，Y)的分布所能达到的最小风险。

随机森林一致性的研究之所以难，原因在于随机森林融合了随机化的因素和确定性的建树过程。具体来说，样本bootstrap和特征子空间的机制是为了构建不那么依赖数据的决策树，但是CART建树的过程是依赖于Gini不纯度的，这是完全依赖于数据的；因此，随机森林一致性的研究基本都是从如何简化这个确定性的建树过程着手。简化必然就会带来性能的损失，所以该领域的研究目标是要做到一致性可以被证明但是性能也不能损失太多。

在一致性方面一个重要的理论突破是由Biau在2008年提出的[36]，他证明了一种原始随机森林的最直接的简化版本，即关于选取分裂特征和分裂值的时候，它是从所有特征里面随机选一个作为分裂特征，同时，从该被选的特征值里随机选一个值当作分裂值。这种简化的随机森林一致性是可以被证明的，但是实验性能很差。紧接着到2012年，Biau把这个领域的研究又往前推进了一步[37]。首先，分裂特征的选择和原始随机森林一样，采用同样的方式构建特征子空间；其次，分裂值的选择是各个特征所有值的中位数；最后，也是通过不纯度下降最多的准则来选取最优的分裂特征和分裂值的组合。Denil等人在2014年提出了另外一种非常接近于原始随机森林的具有一致性的版本[38]，区别点在于分裂值的选取，他们先随机抽取一个所有该特征值的子集，然后在这个子集上寻找最优的分裂。Wang等人在2016年提出了一种概率优化的具有一致性的随机森林，叫伯努利随机森林(Bernoulli Random Forests)[39]。他们采取了两个伯努利分布来控制分裂特征和分裂值的选择，具体来说，以一个伯努利分布B1来控制随机选一个特征或构建特征子空间，以另外一个伯努利分布B2来控制随机选一个分裂值，或是遍历全部分裂值选择不纯度下降最多的。他们提出的伯努利随机森林是目前性能最好的并且具有一致性的随机森林算法。

4 随机森林算法与深度学习之间的关系

随机森林是基于一种树状的分层结构，而深度学习中深度神经网络(Deep Neural Networks)也是一种基于稠密连接的分层的网络结果。我们这章将主要分析随机森林算法与深度神经网络之间的关系，以及把两者相结合的一些研究。

首先，就深度神经网络而言，它有很多层，也有很多参数，而且这些参数全部都会在测试的时候用到。深度神经网络在最后一层分类器之前，我们一般认为它们是一个表示学习的过程，也就是说深度神经网络的分类是基于学习到的特征的。深度神经网络采用的是端到端的训练方式，即基于损失函数的梯度下降。然而，就随机森林而言，它也有很多层，很多参数，但是只有log2N个参数会被用于测试，因为测试样本只会选择唯一一条路径。随机森林的训练是逐层进行的，没有基于目标函数的梯度下降。而且随机森林的建树过程是边建树边分类的，因此，几乎没有或者说有很有限的特征学习的过程。

深度神经网络有很多超参数，调参费时费力，而随机森林几乎没有超参数。深度神经网络有一个很强大的表示学习过程，而随机森林没有。近年来，有一些工作尝试把深度神经网络和随机森林结合在一起。Bulo和Kontschieder在2014年[40]提出了基于神经网络的分裂函数取代之前的Gini不纯度。Kontschieder等人又在2015年[41]进一步提出了深度神经决策森林，他们把随机森林接在了深度神经网络的表示学习过程的后面，把分裂函数变成了随机决策的函数，使其能够通过反向传播来更新整个网络的参数。这大大降低了深度神经网络的参数复杂度，同时，也提升了随机森林的性能。

此外，Zhi-Hua Zhou等人还提出了一种完全基于随机森林的深度结构[42]，他们把随机森林看作是深度神经网络中的一个节点。具体来说，他们采取了级联森林和多粒度扫描来构建深度森林。每个级是决策树森林的一个集合，即集成的集成(ensemble of ensembles)。他们使用了两个完全随机的树森林(complete-random tree forests)和两个原始随机森林。每个完全随机的树森林通过随机选择一个特征在树的每个节点进行分割实现生成。类似地，每个原始随机森林通过随机选择特征子空间，然后选择具有最佳Gini值的特征作为分割。此外，他们应用了滑动窗口来扫描原始特征生成新的特征向量，这些特征向量用作深度森林的输入，可以认为这是对原始特征做了特征变换之后再建树。

5 结语

集成学习是一类非常重要而且实用的方法，它在稍微增加一点复杂度的情况下通常总能提升多个已有分类器的性能，从而在各大竞赛及实际问题中被广泛应用。随机森林等Bagging算法是一种非常具有代表性的集成学习算法，它简单高效、使用方便，在生物信息学、经济学、计算机视觉等众多应用领域取得了巨大的成功。本文从实验性能和理论性质两方面出发对已有的随机森林算法研究进行了总结，最后还阐述了随机森林算法与目前最火热的深度学习之间的关系以及两者相结合的一些工作。作为学术界和工业界均广为应用的一个算法，随机森林在理论性质和应用性能上都还有提升的空间，除了算法一致性仍未完全解决之外，还有以下研究方向，如：为应对日益复杂的分类任务，为充分利用已有的大数据和强大计算能力，如何有效提升模型复杂度、如何利用分层或迭代的方法给出性能更好的集成学习算法；随机森林算法有算法复杂度低而且自带并行化的优势，如何把随机森林算法中的这些思想融入到深度学习的研究当中，加快深度学习的训练并提高其可解释性等，都是值得我们探讨的问题。

[1]Wu X,Kumar V,Quinlan JR,et al.Top 10 algorithms in data mining[J].Knowledge and information systems,2008,14(1):1-37

[2]Quinlan JR.Induction of decision trees[J].Machine learning,1986,1(1):81-106

[3]Quinlan JR.C4.5: programs for machine learning[M].Elsevier,2014

[4]Breiman L,Friedman J,Stone C J,et al.Classification and Regression Trees[M].CRC press,1984

[5]Cortes C,Vapnik V.Support vector machine[J].Machine learning,1995,20(3):273-97

[6]Zhou ZH.Ensemble methods: foundations and algorithms[M].CRC press,2012

[7]Breiman L.Bagging predictors[J].Machine learning,1996,24(2):123-40

[8]Freund Y,Schapire RE.A desicion-theoretic generalization of on-line learning and an application to boosting[C]//In European conference on computational learning theory,1995:23-37

[9]Breiman L.Random forests[J].Machine learning,2001,45(1):5-32

[10]Kwok SW,Carter C.Multiple decision trees[EB/OL].[2018-01-31].https://arxiv.org/abs/1304.2363

[11]Ho TK.The random subspace method for constructing decision forests[J].IEEE transactions on pattern analysis and machine intelligence,1998,20(8):832-44

[12]Acharjee A,Kloosterman B,Visser RG,Maliepaard C.Integration of multi-omics data for prediction of phenotypic traits using random forest[J].BMC bioinformatics,2016,17(5):180

[13]Svetnik V,Liaw A,Tong C,et al.Random forest: a classification and regression tool for compound classification and QSAR modeling[J].Journal of chemical information and computer sciences,2003,43(6):1947-58

[14]Prasad AM,Iverson LR,Liaw A.Newer classification and regression tree techniques: bagging and random forests for ecological prediction[J].Ecosystems,2006,9(2):181-99

[15]Cutler DR,Edwards TC,Beard KH,et al.Random forests for classification in ecology[J].Ecology,2007,88(11):2783-92

[16]Shotton J,Sharp T,Kipman A,et al.Real-time human pose recognition in parts from single depth images[J].Communications of the ACM,2013,56(1):116-24

[17]Lindner C,Bromiley PA,Ionita MC,et al.Robust and accurate shape model matching using random forest regression-voting[J].IEEE transactions on pattern analysis and machine intelligence,2015,37(9):1862-74[18]Baumann T.Decision tree usage for incremental parametric speech synthesis[C]//IEEE International Conference in Acoustics,Speech and Signal Processing.Italy:IEEE,2014:3819-3823

[19]Xiong C,Johnson D,Xu R,et al.Random forests for metric learning with implicit pairwise position dependence[C]//In ACM SIGKDD international conference on Knowledge discovery and data mining,2012:958-966

[20]Verikas A,Gelzinis A,Bacauskiene M.Mining data with random forests: A survey and results of new tests[J].Pattern Recognition,2011,44(2):330-49

[21]Wang Y,Xia ST.Unifying attribute splitting criteria of decision trees by Tsallis entropy[C]//In Acoustics,Speech and Signal Processing,IEEE International Conference,2017:2507-2511

[22]Buntine W,Niblett T.A further comparison of splitting rules for decision-tree induction[J].Machine Learning,1992,8(1):75-85

[23]Liu WZ,White AP.The importance of attribute selection measures in decision tree induction[J].Machine Learning,1994,15(1):25-41

[24]Nowozin S.Improved information gain estimates for decision tree induction[EB/OL].[2018-01-31].https://arxiv.org/abs/1206.4620

[25]Serrurier M,Prade H.Entropy evaluation based on confidence intervals of frequency estimates: Application to the learning of decision trees[C]//In International Conference on Machine Learning,2015:1576-1584

[26]Esposito F,Malerba D,Semeraro G,et al.A comparative analysis of methods for pruning decision trees[J].IEEE transactions on pattern analysis and machine intelligence,1997,19(5):476-91

[27]Wold S,Esbensen K,Geladi P.Principal component analysis[J].Chemometrics and intelligent laboratory systems,1987,2(1-3):37-52

[28]Rodriguez JJ,Kuncheva LI,Alonso CJ.Rotation forest:A new classifier ensemble method[J].IEEE transactions on pattern analysis and machine intelligence,2006,28(10):1619-30

[29]Skurichina M,Duin RP.Combining Feature Subsets in Feature Selection[J].Multiple classifier systems,2005,3541:165-75

[30]Mart'ınez M,Kak A C.Pca versus lda[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(2):228–233

[31]Guyon I,Elisseeff A.An introduction to variable and feature selection[J].Journal of machine learning research,2003,3(3):1157-82

[32]Ye Y,Wu Q,Huang J Z,et al.Stratified sampling for feature subspace selection in random forests for high dimensional data[J].Pattern Recognition,2013,46(3):769–787

[33]Nguyen T T,Zhao H,Huang J Z,et al.A new feature sampling method in random forests for predicting high- dimensional data[C]//In Advances in Knowledge Discovery and Data Mining,2015:459–470

[34]Wang Y,Xia S T.A novel feature subspace selection method in random forests for high dimensional data[C]//In International joint conference on neural networks,2016:4383–4389

[35]Amaratunga D,Cabrera J,Lee Y S.Enriched random forests[J].Bioinformatics,2008,24(18):2010–2014

[36]Biau G,Devroye L,Lugosi G.Consistency of random forests and other averaging classifiers[J].Journal of Machine Learning Research,2008,9(9):2015-2033

[37]Biau G.Analysis of a random forests model[J].Journal of Machine Learning Research,2012,13(4):1063-1095[38]Denil M,Matheson D,De Freitas N.Narrowing the gap: Random forests in theory and in practice[C]//In International conference on machine learning,2014

[39]Wang Y,Tang Q,Xia ST,et al.Bernoulli Random Forests:Closing the Gap between Theoretical Consistency and Empirical Soundness[C]//In International joint conference on artificial intelligence,2016:2167-2173

[40]Rota Bulo S,Kontschieder P.Neural decision forests for semantic image labelling[C]//In IEEE Conference on Computer Vision and Pattern Recognition,2014:81-88

[41]Kontschieder P,Fiterau M,Criminisi A,et al.Deep neural decision forests[C]//In IEEE International Conference on Computer Vision,2015:1467-1475

[42]Zhou ZH,Feng J.Deep forest:Towards an alternative to deep neural networks[EB/OL].[2018-01-31].https://arxiv.org/abs/1702.08835