木材干燥理论架构及其数学表达的研究简报
林 铭,杨庆贤,饶久平,谢拥群,廖益强,魏 微
(福建农林大学 材料工程学院,福建 福州 350002)
考虑到木材干燥过程发生的热质迁移及其交叉作用的复杂性。因此,必须从普遍性的角度,研究温度梯度、湿度梯度、压力梯度引起的热量传导输运、水分物质扩散迁移、水蒸气渗透迁移及其相互耦合效应的普适规律,即建立木材干燥过程的热质迁移定律。该定律将作为木材干燥理论架构的一个基础。同时,考虑到木材干燥过程,在木材介质内部各点上的温度和湿度这两个重要物理量的数值不仅是空间的点函数,而且是时间的函数。因此,必须研究温度场和湿度场随时空变化的普适规律,即建立木材干燥过程介质内部温度场和湿度场的非稳态偏微分方程组。该偏微分方程组将成为木材干燥理论架构的另一基础。然而,无论是建立热质耦合迁移定律,还是建立场偏微分方程组,其数学推导过程均极其复杂。考虑到篇幅有限,本文首先将以简报形式报道木材干燥过程热质耦合迁移定律和场偏微分方程组的数学表达式,而它们复杂的数学推导过程,将在后续发表。
1 木材干燥过程热 — 质耦合迁移定律
如果把干燥木材介质看作一个系统,则该系统既不是孤立系统也不是封闭系统,而是一个开放系统。系统既然是开放的,那么系统在干燥过程所发生的热量传导过程、水分扩散过程和水蒸气渗透过程就是系统与外界之间发生的能量交换过程、物质交换过程和熵交换过程。系统与外界发生这些能量、物质和熵的交换将引起系统热力学能的改变和熵的增加。系统热力学能是一个状态函数。选择适当的状态参变量,例如本文选择熵、体积和各组元的摩尔数作为系统参变量。应用钱学森的《物理力学》[13]的理论和方法,对系统热力学能的变化和熵的产生率进行分析、研究和数学推导,便可以从理论上导出木材干燥过程热 — 质耦合迁移定律为
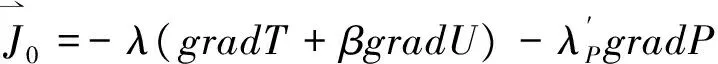
(1)
(2)
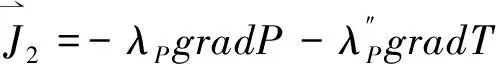
(3)
式(1)是对木材干燥过程发生的热量迁移、液态水分迁移和水蒸气渗透迁移及其相互耦合作用从理论上做出的完整的定量描述。
2 木材干燥过程木材介质内部的温度场和湿度场方程
温度和湿度是木材干燥过程两个重要的物理量。他们的数值大小不仅是空间的点函数,而且随时间而变。因此温度场和湿度场都是非稳恒场。
应用物理学的相关知识和适当的数学工具,可直接从(1)、(2)、(3)式导出温度场和湿度场方程为
(4)
(5)
(6)
式(4)、(5)、(6)是一组非稳态的二阶偏微分方程组。式中:div是散度微分算符,r和L分别是液态水的汽化率和汽化热。当木材干燥过程的初始条件和边界条件随之确定后,通过求解(4)、(5)、(6)式微分方程组,便可得到干燥过程木材内部任一点在任意时刻的温度和湿度的数值大小。
3 分析与结论
(7)
(8)
不难看出:(7)、(8)式就是目前《木材干燥》教科书[14-15]中,关于一维的热质迁移定律的表述。说明它仅仅是(1)、(2)、(3)式普遍热质耦合迁移定律在不参考渗透现象和Dufour效应情况下的一种特例而已。
在P→0的极限情况下,(1),(2),(3)式将变为
(9)
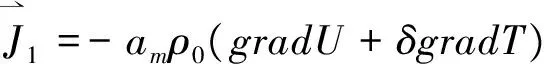
(10)
显而易见,(9)、(10)式是我们前期一个不考虑渗透现象及其对热质迁移耦合作用的阶段性研究成果[6]。但是该成果因不考虑渗透现象而无法全面地、正确地反映木材干燥过程传热传质问题。因为当干燥温度大于50 ℃时,干燥介质内部水分蒸发已相当明显,而木材干燥温度一般都大于50 ℃,对高温干燥而言,更可超过100 ℃,这时渗透现象及其渗透对传热传质的影响是不能不考虑的学术问题。
由(1)、(2)、(3)式表达的木材干燥过程热质耦合迁移定律是对木材干燥过程所发生的各种“流”(热流、扩散流和渗透流)与引起这些“流”的各种“力”(温度梯度、湿度梯度和压力梯度)之间交叉耦合作用的定量描述。
由(4)、(5)、(6)式表达的是一组木材干燥过程介质内部温度场T(x,y,z,t)和湿度场U(x,y,z,t)与空间变量(x,y,z)和时间变量(t)之间关系的偏微分方程组。求解该微分方程组,便可得到干燥过程木材介质内部各点在不同时刻的温度T和湿度U这两个重要物理量,为干燥工艺条件的制定与调控提供科学依据。
由(1)、(2)、(3)式迁移定律和(4)、(5)、(6)式干燥场微分方程组结合成为一个完备的、严谨的木材干燥理论架构系统。
参考文献:
[1] 俞昌铭.多孔材料传热传质数值分析[M].北京:清华大学出版社,2011.
Yu C M.Numerical analysis of heat and mass transfer of porous materials[M].Beijing:Tsinghua University Press,2011.
[2] 赵景尧.木材干燥过程热质迁移数学模型研究现状[J].北京林业大学学报,2015,37(7):123-128.
Zhao J Y.Present status of research on mathematical models of heat and mass transfer during wood drying[J].Journal of Beijing Forestry University, 2015,37(7):123-128.
[3] Rees D A S.The onset of Darcy-Brinkman convection in a porous layer:an asymptotic analysis[J].Int J Heat and Mass Transfer,2002,45(11):2213-2220.
[4] Dedic A.Simplifying convective heat and mass transfer in moisture desorption of beech wood by introducing characteristic transfer coefficients[J].Holzals Roh and Werkstoff,2000,58(1/2):96-101.
[5] 杨庆贤.不可逆过程热力学研究木材干燥规律[J].山东科技大学学报,2003,22(s1):105-106.
Yang Q X.On laws in wood drying by irreversible thermodynamics[J].Journal of Shandong University of Science and Technology,2003,22(s1):105-106.
[6] 谢拥群,陈瑞英,杨庆贤,等.木材干燥过程热质迁移及其耦合关系[J].林业科学,2004,40(1):148-153.
Xie Y Q,Chen R Y,Yang Q X,et al.Heat and mass transfer and coupling effect in wood drying[J].Scientia Silvae Sinicae,2004,40(1):148-153.
[7] Incropera F P,De Witt D P.Fundamentals of heat and mass transfer[J].5th ed.New York:John Wiley & Sons,2002:389-395.
[8] Lu L,Tang J,Ran X.Temperature and moisture changes during microwave drying of sliced food[J].Drying Technology,1999,17(3):413-432.
[9] Perre P,Turner I.A 3-D version of transpore:a comprehensive heat and mass transfer computational model for simulation the drying of porous media[J].Heat and Mass Transfer,1999,42(24):4501-4521.
[10] Gong L,Plumb O.The effect of heterogeneity on wood drying.2.experimental results(Abstract available)[J].Drying Tech,1994,12(8):2003-2026.
[11] Nijdam J J,Langrish T A G,Keey R B.A high temperature drying model for softwood timber[J].Chem Eng Sci,2000,55(18):3585-3598.
[12] Defo M,Fortin Y,Cloutier A.Modeling superheated steam vacuum drying of wood[J].Drying Technology,2004,22(10):2231-2253.
[13] 钱学森.物理学讲义[M].北京:科学出版社,1992:274-292.
Qian X S.Physics handouts[M].Beijin:Science Press,1992:274-292.
[14] 南京林产工业学院.木材干燥[M].北京:中国林业出版社,1984.
Nanjing Forest Industrial College.Dry wood[M].Beijing:China Forestry Press,1984.
[15] 朱政贤.木材干燥[M].2版,北京:中国林业出版社,1992.
Zhu Z X.Dry wood[M].2nd ed,Beijing:China Forestry Press,1992.

