基于改进灰靶理论的航空发动机健康监测方法*

张 建， 曹愈远， 李艳军， 张丽娜

(1.南京航空航天大学民航学院 南京，211106) (2.中国航空发动机集团有限公司商用航空发动机有限责任公司 上海，200241)

引 言

航空发动机工作环境恶劣、零组件数量大、故障模式种类多、工作寿命长，其使用安全问题十分严酷，研究和保障具有较大难度[1]。航空发动机健康监测的原理是对其监测参数进行分析，发掘其中隐藏的状态信息。常见的监测参数包括油液参数[2]、振动参数[3]和气路参数[4]等。传统的健康监测方法是将发动机测量数据与标准模型计算得到的数据进行比较，根据差的大小判别发动机状态。

目前在状态评估领域运用较多的是基于知识的智能诊断方法，如神经网络[5]、专家系统[6]、支持向量机[7]等，但是这些方法在运用中存在一些自身的不足。如神经网络存在网络结构选择、容易陷入局部极值等；专家系统存在知识不完整、适应性差等；支持向量机存在惩罚因子、核函数选择等问题。

航空发动机是极其复杂的非线性系统，测取全部性能参数不太现实，并且得到的性能数据也不完整。而我国邓聚龙教授在上世纪80年代初期创立的灰色理论正是用于处理这种部分信息已知、部分信息未知的贫信息系统的有效方法。发展至今，灰色理论成为一门包括众多灰色模型的新兴学科。在对灰靶决策权重系数优化基础上，笔者首次将灰靶决策理论用于航空发动机健康监测，讨论了状态等级划分、可靠性和剩余寿命分析以及故障诊断等问题，具有探索性和创新性。

1 方法简介

笔者提出的基于改进灰靶理论的航空发动机健康监测方法的研究流程如图1所示。主要分为两步：a.理论模型，用层次分析法计算静态权重，用熵理论改进权重，综合后得到灰靶决策的权重系数，建立灰靶决策理论模型；b.模型运用，结合航空发动机性能参数监测数据及可靠性和故障诊断知识，实现发动机状态等级划分、可靠性和剩余寿命分析以及故障诊断。

图1 健康监测算法流程图Fig.1 Flow chart of health monitoring algorithm

2 改进灰靶决策模型

2.1 灰靶决策

灰靶决策理论的原理是：选定具有特定意义的某个向量作为靶心，计算标准向量与靶心的靶心度，得到各标准向量的靶心度作为决策依据，然后计算输入向量的靶心度与标准向量靶心度进行比较，根据决策规则得到结论[8]。灰靶决策流程如图2所示，其具体计算过程如下。

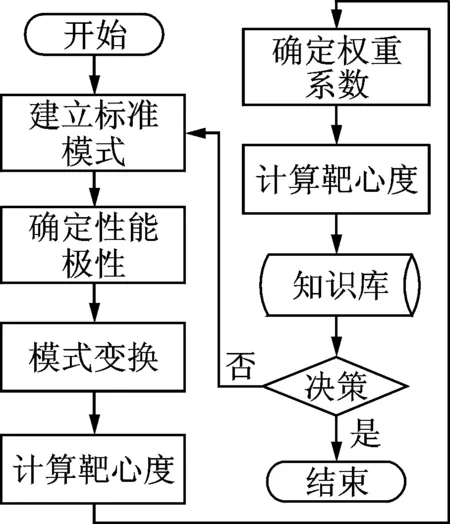
图2 灰靶决策流程图Fig.2 Flow chart of grey target decision

1) 建立标准模式：假设ωi是航空发动机的第i个状态，ω(k)为发动机第k个性能参数值，ωi⟹k∈K={1,2,…,n},i∈I={1,2,…,m}，则对于性能参数ω(k)有ω(k)= {ω1(k),ω2(k),…,ωm(k) }，∀ωi(k)∈ω(k)⟹i∈I={1,2,…,m}。

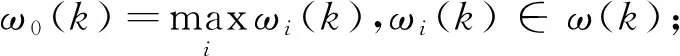
2) 计算靶心系数：首先进行靶心换算，将标准状态模式转化为标准靶心，令T为变换，Tω0=x0,x0=(x0(1),x0(2),…,x0(k))=(1,1,L,1)，x0为变换后的标准靶心，即1化靶心。对待识别的模式进行变换Tωi(k)=xi(k)，则

(1)

根据灰色系统理论，靶心系数γ(x0(k),xi(k))的计算公式为

(2)

其中：Δ0i(k)=|x0(k)-xi(k)|=|1-xi(k)|，一般情况下ρ=0.5。

3) 按2.2节中方法确定权重系数η1,η2,…,ηn。

4) 计算靶心度：状态Xi的靶心度γ(x0,xi)为

(3)

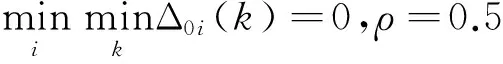
(xi(k))≤1,k=1,2,…,m)

即，γ(x0,xi)≥0.333。因此有0.333以下各档无意义。

5) 根据靶心度和知识库作出决策。

2.2 权重优化

本研究通过综合层次分析法和熵权法两种方法来得到权重，先用层次分析法依据历史数据计算性能参数的静态权重；再用熵权法依据性能参数变化量确定其改进权重，并用于修正静态权重以得到综合权重ηk[9]。

1) 用层次分析法(analytic hierarchy process，简称AHP)确定静态权重：对n个性能参数的重要程度赋值，按照两两比较结果得到的判断矩阵为

(4)

其中：αi/αj为第i个性能参数相对于第j个性能参数的重要程度。

然后用矩阵权值方法，为满足一致性检验条件的判断矩阵A找一个最优权值向量W=(β2,β2,…,βn)T，即为性能参数权值向量。

2) 用熵权法确定改进权重：对于有n个性能参数，m个评价对象的多目标评估问题，其灰靶系数矩阵为

(5)

(6)

则第i个性能参数的信息熵定义为

(7)

其中：k=1/lnm。

其权重定义为

(8)

3) 在求得各性能参数的熵εi后，修正初始的静态权重ηk得到最终的综合权重ηk，表示为

(9)

3 航空发动机健康监测

3.1 状态等级划分

依据航空发动机故障特点规定了4个故障严酷度等级，即：I类(灾难性)、ll类(致命性)、lll类(临界性)和VI类(轻度性)。ARP4754和国军标GJB1391中将故障概率等级分为如表1所示5个等级[10]，这是故障判别的重要量值。

表1 故障模式及概率

故障发生概率和故障严重程度关联，发生概率越高则其严酷度越低。因此，将靶心度分为5级，其中第1级相当于灾难性故障，对应于很少和极少发生，概率取0～1%；第2级相当于致命性故障，对应偶然发生，概率取1%～10%；第3级相当于临界性故障，对应可能发生，概率取10%～20%；第4级相当于轻度性故障，对应经常发生，概率为20%以上；第5级相当于正常状态。

根据专家经验，如果状态参数与标准状态参数作为靶心的灰靶的靶心度小于0.95即视为故障，则故障靶心度范围为[0.333,0.950]。因为第1级故障的分布百分比为0～1%，则0.333+1%×(0.950-0.333)=0.339，即第1级的分级靶心度为[0.333，0.339]。相应的将航空发动机状态评估分级整理如下[14]。

第1级：[0.333，0.339]，灾难性故障；

第2级：[0.339，0.395]，致命性故障；

第3级：[0.395，0.457]，临界故障；

第4级：[0.457，0.950]，轻度故障；

第5级：[0.950，1.000]，运行正常。

3.2 可靠性和剩余寿命

可靠性分析与剩余寿命评估是航空发动机安全性分析中重要的一部分[11]。各国学者在可靠性研究方面做了大量工作。但是，传统可靠性方法以大样本数据为支撑，而航空发动机失效样本不足[12]。

本研究以新的监测值为靶心得到的靶心度反映了发动机当前运行状态与初始状态的相似度，靶心度越大表示当前状态越安全，即可靠性越高；靶心度越小表示当前状态越不安全，即可靠性越低。因此可用靶心度来衡量航空发动机的运行可靠性。根据可靠性计算结果和航空发动机性能衰退曲线，可得发动机的剩余寿命。故靶心度γi和可靠性P的换算公式如下

Pi=(ri-0.333)/(1-0.333)

(10)

根据可靠性和航空发动机性能退化曲线，可近似得到发动机工作循环数以及剩余寿命。

3.3 故障诊断

故障诊断是航空发动机安全性的重要分支，基于人工智能算法的故障诊断过程一般分为两个过程，即训练学习过程和诊断运用过程。首先用训练样本进行学习，得到各故障的靶心度；然后用训练好的模型对测试样本进行故障诊断[13]。笔者提出如下基于灰靶决策分析法的故障模式识别方法：

1) 用已知各类型故障样本作为训练样本，计算所有样本与靶心的靶心度，并求各类型故障靶心度平均值，此值作为该故障的靶心度；

2) 若多个故障靶心度之差小于阈值μ，则认为两故障相近，将其先作为一个大类与其他故障进行一级划分，然后增加参数维数，计算靶心度，对相似故障进一步划分；

3) 计算待诊断样本与靶心的靶心度，与其最接近的故障样本即为其对应故障。

4 实例验证

现以项目组与某航空公司合作中获取的某型航空发动机性能参数监测数据和其他资料为例，验证笔者提出方法的科学性。取表征航空发动机故障的3个关键参数作为文中的性能指标，分别为排气温度(exhaust gas temperature ，简称EGT)、高压压气机转速(core shaft speed，简称CSS)以及燃油流量(fuel flow，简称FF)。以新发动机运行初期的性能参数值作为靶心。

4.1 等级划分实例

由于发动机实际运行中缺少灾难性故障和致命性故障数据，因此本研究只以发动机正常状态、轻度故障状态、临界故障状态下的各1组性能参数值为例展示算法的运算过程，选取新发动机监测数据作为决策的靶心。各状态参数值如表2所示。

表2 验证样本

根据表2，则靶心为

ω0=(ω0(1),ω0(2),ω0(3))=

(593.5,94.312,2 776)

对其他状态进行归一化得

其靶心系数为

对3个性能参数的重要程度赋值

α=(α1,α2,α3)=(1,0.95,0.90)

按照两两比较结果得到的判断矩阵A为

矩阵A满足一致性检验条件，则参数权值向量为A的特征向量，即

W=(0.351，0.333，0.316)T

灰靶系数矩阵经归一化为

其权重定义为

ε=(0.139,0.537,0.323)

其综合权重为

η=(0.612,0.151,0.237)

靶心度为

γ=(0.951,0.551,0.448)

由3.1节中等级划分标准知，其划分结果与对应实际状态一致。增大验证的数据量，用Matlab进行编程计算，其验证结果统计如表3所示。

表3 算法准确性统计表

结果表明，笔者提出的方法具有较高准确率，对数据进行分析发现，只有在一些临界或者极端情况下算法才会出现错误，这类问题在人工划分时同样会出现，是由边界模糊造成，故可认为本算法具有适用性。

4.2 可靠性及剩余寿命实例

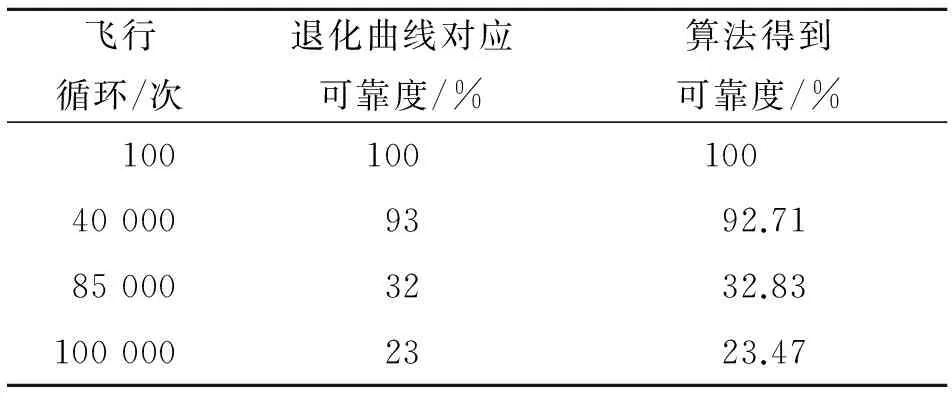
航空公司给出的该型发动机性能退化曲线处理后如图3所示，根据文中3.1和3.2算法计算具有代表性的不同飞行循环次数对应的可靠度，鉴于篇幅，不列出计算过程，其结果如表4所示。可以看出

算法计算得到的可靠性与根据性能曲线得到的可靠性非常接近，说明算法具有较高的准确度。相反可根据可靠性值计算对应的运行循环数以及剩余寿命，在此不累述。

图3 性能退化曲线Fig.3 Performance degradation curve

飞行循环/次退化曲线对应可靠度/%算法得到可靠度/%100100100400009392.71850003232.831000002323.47

4.3 故障模式识别实例

以高压涡轮5种实际典型轻度故障为例验证算法的模式识别性能，故障类型为：工作叶片损坏、外密封间隙大、工作叶片磨损、导向叶片烧损和导向叶片损坏。以上述5类轻度故障数据各10组作为训练样本，计算各类故障靶心度，结果如表5所示。

表5 训练样本

从表中可看出并未出现一步不可分情况，以另外50组以上5类轻度故障数据作为测试样本，计算靶心度，选取上表中靶心度最接近值，对应故障类型即为模式识别结果，用Matlab进行编程，其诊断结果如图4所示，从图中可以看出有2组错误，算法准确率为96%，满足业内对航空发动机故障诊断的要求。

增大验证的数据量，其验证结果统计如表6所示。

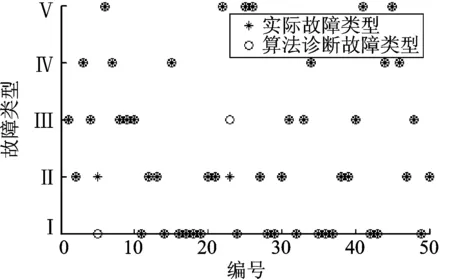
图4 诊断结果Fig.4 Diagnosis results

表6 诊断准确性统计表

Tab.6 Statistical table of diagnosis accuracy

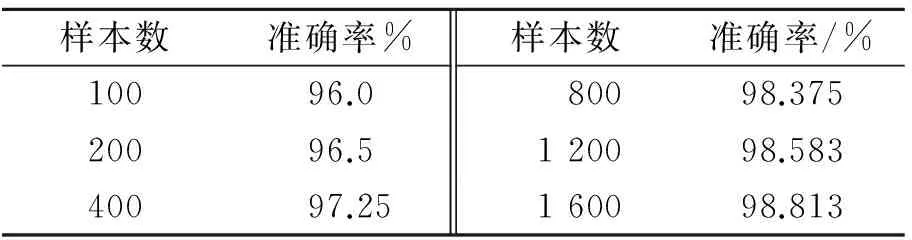
样本数准确率%样本数准确率/%10096.080098.37520096.5120098.58340097.25160098.813

随着样本量增加，降低了个别不合理样本对整体的影响，算法诊断率逐渐提高。研究诊断错误的数据发现，除去明显不合理样本外剩余都是临界无故障样本被误诊为故障，然而虽将其错诊为故障造成虚警，但是虚警率不高且能够保证系统的安全。由此可见，笔者提出的算法具有很好的工程可行性和实用性。

5 结束语

基于改进灰靶理论提出的航空发动机健康监测方法可以有效的实现状态的评估、可靠性估算、寿命预测以及发动机故障模式识别。笔者提出的基于灰靶决策的航空发动机状态评估算法以灰靶理论为主体，通过层次分析法和熵理论综合优化其权重算法，根据故障严酷度和发生概率划分状态等级，根据靶心度分析其所处状态和可靠度以及剩余寿命，另外可依据典型故障靶心度来识别具体故障。经航空发动机气路性能参数验证结果知，笔者提出的算法可以有效实现对航空发动机状态的监测。

[1] 尉询楷，杨立，刘芳，等.航空发动机预测和健康管理[M].北京:国防工业出版社,2014:27-34.

[2] 李艳军，左洪福，吴振峰．基于磨粒分析方法的发动机磨损故障智能诊断技术[J].南京航空航天大学学报,2001,33(3):221-226.

Li Yanjun, Zuo Hongfu, Wu Zhenfeng. Intelligent diagnostics for engine wear failure based on debris analysis[J].Journal of Nanjing University of Aeronautics and Astronautics, 2001, 33(3):221-226. (in Chinese)

[3] 仝兆景，石秀华，王文斌，等. 基于优化分簇贝叶斯网的转子振动故障诊断[J].振动、测试与诊断, 2014,34(2):237-241.

Tong Zhaojing, Shi Xiuhua , Wang Wenbin, et al. Generator rotor vibration fault diagnosis based on optimization clustering Bayesian network [J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(2):237-241. (in Chinese)

[4] 刘占生，曹智选，沈勇，等. 某型涡轴发动机气路故障数值仿真[J]. 振动、测试与诊断, 2014,34(5):844-850.

Liu Zhansheng, Cao Zhixuan , Shen Yong, et al. Numeric simulation of gas-path fault for a turbo shaft [J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(5):844-850. (in Chinese)

[5] 雷达，钟诗胜．用集成过程神经网络预测民航发动机振动趋势[J]. 振动、测试与诊断, 2015,35(1):137-141.

Lei Da, Zhong Shisheng. Trend prediction of civil aircraft engine vibration signal using ensemble process neural networks [J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(1):137-141. (in Chinese)

[6] 陈果，左洪福．基于知识规则的发动机磨损故障诊断专家系统[J].航空动力学报,2004,19(1):23-29.

Chen Guo, Zuo Hongfu. Expert systems of engine wear fault diagnosis based on knowledge rule[J].Journal of Aerospace Power,2004,19(1):23-29.(in Chinese)

[7] 徐启华,师军. 基于支持向量机的航空发动机故障诊断[J].航空动力学报,2005,20(2):298-302.

Xu Qihua, Shi Jun. Aero-engine fault diagnosis based on support vector machine[J]. Journal of Aerospace Power, 2005,20(2):298-302. (in Chinese)

[8] 及红霞.基于改进灰靶理论的变压器健康状态评估[D].北京：华北电力大学，2010.

[9] 郑玲峰，王建元，白志亮，等.用改进灰靶理论评价变压器状态[J] .中国电力,2011,44(1):28-31.

Zheng Linfeng, Wang Jianyuan, Bai Zhiliang, et al. Transformer state evaluation based on improved gray

target theory[J] .Electric Power,2011,44(1):28-31. (in Chinese)

[10] 李世林.基于BP神经网络的航空发动机失效模式与故障影响分析[D].南京：南京航空航天大学，2003.

[11] 任淑红.民航发动机性能可靠性评估与在翼寿命预测方法研究[D].南京：南京航空航天大学，2010.

[12] 孙闯，何正嘉，张周锁，等.基于状态信息的航空发动机运行可靠性评估[J] .机械工程学报,2013,49(6):30-37.

Sun Chuang, He Zhengjia, Zhang Zhousuo, et al. Operating reliability assessment for aero-engine based on condition monitoring information[J]. Journal of Mechanical Engineering, 2013, 49(6):30-37. (in Chinese)

[13] 刘丽娜.灰靶理论在液压泵故障模式识别中的应用[D] . 秦皇岛：燕山大学，2011.