寿命周期构型变化类橡胶减振器使用寿命评估*

金 著， 何 琳， 赵应龙

(1．海军工程大学振动与噪声研究所 武汉,430033) (2.船舶振动噪声重点实验室 武汉,430033)

引 言

橡胶减振器具有优良的隔振抗冲击效能，且结构可设计性强，在汽车、舰船、航空等隔振需求大、空间狭小的领域大量应用。由于老化、蠕变、疲劳等现象的存在，橡胶材料的性能会随时间推移而逐渐退化，进而导致橡胶减振器使用寿命终结[1-2]。现有橡胶产品的寿命分析理论主要关注橡胶材料的机械疲劳寿命，其进行疲劳寿命计算的输入通常是产品在一个循环载荷周期内的应变谱，通过建立产品应变谱、材料疲劳损伤参量以及材料疲劳寿命之间的关系，进而计算产品在该应变谱下的疲劳循环次数，并以此作为产品的疲劳寿命[3-6]。但是，由于橡胶减振器通常既起到隔振抗冲的作用，又起到托承被隔振设备的作用，在实际使用情况中，橡胶减振器多是由老化、蠕变、疲劳等因素综合作用而损坏的[7]。因此，仅用一个输入应变谱计算出的橡胶减振器疲劳寿命评估结果是不够准确的。随着设备总体隔振设计深度的不断提高，对橡胶减振器的寿命设计与评估提出了更高的要求[8-9]。

1 失效理论

1.1 橡胶减振器分类

图1 橡胶制品疲劳寿命计算思路Fig.1 Fatigue life calculating thought of rubber products

橡胶减振器疲劳寿命理论计算思路如图1所示，不同计算理论的疲劳损伤参量的选取各不相同，常用的有最大主应变、应变能密度、裂纹扩展率等[10]。这些理论在计算橡胶产品疲劳寿命时，均需以有限元仿真计算的产品在周期载荷谱作用下的周期应变谱作为计算输入，并用产品在该应变谱下的疲劳寿命作为产品的疲劳寿命。这种思路的使用前提是橡胶产品在整个寿命周期内，在周期载荷谱作用下产生的应变谱不变，或仅发生微小改变。该思路巧妙地解决了长寿命产品的疲劳计算载荷谱输入的问题，适用于各类回转型设备及承受周期性载荷的减振器，如轮胎、轴承支座等[11-12]。但是，对于起承重减振作用的橡胶减振器，由于其橡胶弹性体在寿命周期内会因性能退化而发生较大的结构形式变化，导致在同样承重和振动条件下，不同寿命阶段减振器弹性体的构型均不相同，因而对应的应变谱也不相同，故不能仅以寿命初期在循环载荷下对应的应变谱代表整个寿命阶段的应变谱来作疲劳寿命计算。

针对现有的橡胶减振器寿命计算理论的局限性，笔者提出将橡胶减振器分为两类：第一类是寿命周期构型不变类橡胶减振器，第二类是寿命周期构型变化类橡胶减振器。仅前者适用于现有疲劳寿命计算理论。寿命周期构型变化类橡胶减振器的使用寿命评估是本研究的重点。这类橡胶减振器的特点归纳如下：

1) 功能上既减振抗冲，又支撑承重，且上述功能均由橡胶弹性体实现；

2) 机械载荷上可理解为力控制，而非位移控制；

3) 弹性体的构型随时间变化而变化；

4) 相同载荷谱在不同寿命阶段会产生不同的应变谱；

5) 弹性体构型对减振器性能有较大影响。

满足上述5个特点的橡胶减振器就可认为是第二类橡胶减振器，笔者选取的研究对象为船舶上大量使用的某型橡胶减振器，正属于此类，其结构示意图如图2所示。

图2 某型船用橡胶减振器结构示意图Fig.2 Structure diagram of a marine rubber isolator

1.2 失效机理分析

结合此型减振器实际使用情况和图2可知，其在设备重力、振动、环境因素等的作用下，橡胶弹性体包裹的上端金属接头会发生垂向位移，随着橡胶材料性能的逐渐退化，金属接头垂向向下的位移量也将逐渐增加，直到橡胶弹性体块的底部与基座发生柔性碰撞(称为触底)。此时，减振器刚度特性发生较大改变，且由于垂向位移量较大导致被支撑设备产生超出许用范围的跟随位移，可认为减振器已经失效。图3是实际使用中该型减振器失效形式照片。

图3 橡胶减振器失效形式Fig.3 Failure mode of the rubber isolator

由于减振器弹性体材料在老化、蠕变及疲劳等综合因素的作用下发生了性能退化致使减振器结构发生巨大改变，这种导致减振器失效的现象在实际使用过程有时会在弹性体材料发生疲劳断裂前就出现。因此，单纯计算减振器弹性体材料的疲劳寿命并不能准确预报减振器实际使用寿命。表1列出了橡胶减振器此类失效现象的失效物理相关因素。

表1 橡胶减振器失效物理诸因素

1.3 寿命特征参数选取

橡胶减振器失效过程属于退化型过程，需选定减振器的某一性能指标作为寿命特征参数，并划定该指标的失效阀值。寿命特征参数需具备以下特点：易于测量；测量对减振器不具有破坏性；准确评估寿命状态；定义清晰，没有歧义；表述简便。

对于寿命周期构型变化类橡胶减振器，应选取能够准确反映其构型变化幅度的参数作为寿命特征参数。综合上述特点，以本研究对象为例，最合适的寿命特征参数是减振器的垂向变形量，也即高度变化量。研究对象的橡胶弹性体底部与基座间间隙约为10 mm，这是减振器垂向变形量的极限值。现以9 mm垂向变形量(振动位移均值)作为减振器的失效判定准则，以9.5 mm垂向变形量(振动位移峰值)作为试验截止条件之一。

2 加速退化试验

2.1 力控制温度加速试验

由于不同橡胶减振器构型的多样性以及传统疲劳计算原理的局限性，对于构型变化类橡胶减振器在综合应力作用下的失效寿命评估尚无通用可行的理论和有限元仿真计算方法。因此，通过直接对产品开展寿命试验仍然是目前最可行可信的方法。

橡胶减振器通常具有数年的使用寿命，普通寿命试验的时间和资金成本都无法接受，需开展加速试验。本研究选择温度作为加速应力，设4个温度应力等级。对于较低的温度应力等级，其加速系数较小，不能使减振器在可接受的时间范围内失效，需开展加速退化试验，利用试验件的退化轨迹模型和退化试验数据外推出试验应力状态下的寿命[13]。

疲劳试验的机械载荷通常是位移控制，其目的是便于计算被试件的应变谱。对于构型变化类橡胶减振器，为真实反映其寿命周期内构型变化规律，需将试验机械载荷设定为力控制，并实时记录施加在减振器上的力和位移参数。

2.2 试验样件及条件

本研究的试验对象额定承载为3 kN，固有频率约12 Hz，试验使用带环境箱的MTS弹性体试验机开展，如图4所示。温度加速应力设置4档，分别为120，89，63和40 ℃，每一温度应力等级安排4个样件试验，共16组试验(分别编号为1.1～4.4)。机械载荷设置为：按正弦波形加载动态振动载荷，均值3 kN，幅值为300 N，频率为12 Hz。加速退化试验截止条件设置为被试减振器垂向位移量峰值达到9.5 mm或试验总时长达到120 h。

图4 被试减振器安装及环境箱Fig.4 Installation of the tested isolator and the environmental chamber

图5 试验机记录的数据Fig.5 MTS test system recorded data

使用弹性体试验机开展寿命试验具有数据量丰富，数据实时性和可挖掘性强的优势。试验过程中，由MTS试验机实时采集减振器的力和位移，环境箱温度以及时间数据，每小时采集1次，每次采集6个载荷循环(即0.5 s)的数据，采样频率为2 048 Hz。图5为试验采集的数据示例(编号2.1的试验数据，下同)，图5(b)中x轴数据为试验小时数。

2.3 试验数据预处理

将不同试验采集时段的位移数据取均值，即可得到试样的垂向变形量和循环次数的曲线，如图6所示。图6～8中横坐标表示循环次数，但为方便观察，在坐标轴上标注的数值对应的是试验时间，单位为小时，载荷循环次数是无量纲单位，由小时数乘以每小时循环次数43 200次即可得到。

图6 垂向变形量与循环次数关系曲线Fig.6 Curve of vertical displacement and load cycles

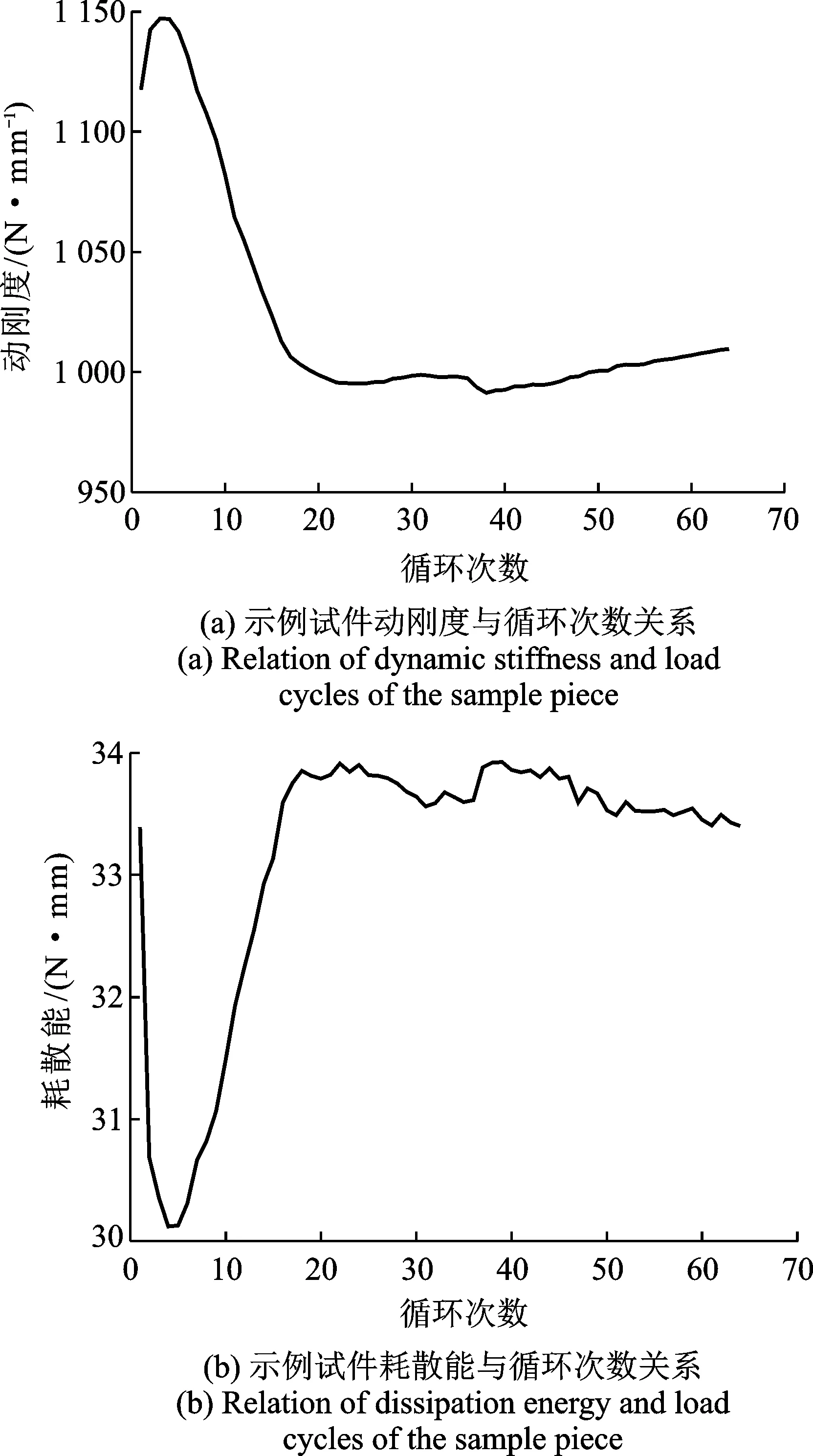
图7 动刚度和耗散能试验分析结果Fig.7 Analysing result of dynamic stiffness and dissipated energy

图8 示例试件垂向变形量幂次拟合效果Fig.8 Power fitting result of the vertical displacement data of the example

在正弦波形力控制条件下，减振器迟滞回线呈近似椭圆形状，可拟合出减振器迟滞回线方程，进而计算在试验条件下的减振器动刚度和耗散能。使用非线性回归拟合减振器不同时间段的力位移数据，拟合方程为标准斜椭圆方程，如式(1)

a1x2+a2xy+a3y2+a4x+a5y+a6=0

(1)

其中：x和y分别为力和位移数据；a1～a6分别为拟合参数。

动刚度Kglo和耗散能Edis的计算式分别为

(2)

(3)

将试验期间被试件每小时的力位移数据均做上述处理，可得试件动刚度和耗散能随载荷循环次数的变换趋势，如图7所示。从计算结果可见，在试验初期，示例试件动刚度由于应变结晶效应的存在而呈上升趋势；然后，橡胶材料在环境因素和机械载荷的综合作用下，进入快速退化阶段，分子链大量断裂，呈现动刚度近似恒速下降的趋势；快速退化阶段结束后，橡胶进入稳定硬化阶段，在此阶段橡胶材料将逐渐硬化，并出现裂纹，直至最后完全失效。试验结果与部分学者研究结果吻合[14]。

从多次试验结果来看，当试件垂向变形量超过失效阈值9 mm时，其动刚度变化量均较小，通常在初始值的15%以内，可以认为减振器在刚度特性上尚未发生失效，这也佐证了选取垂向变形量为本研究对象寿命特征参数的合理性。

3 使用寿命评估

3.1 退化轨迹模型及伪失效寿命求解

图7中曲线即为被试减振器寿命特征参数的退化轨迹曲线，为建立其退化轨迹模型，需对曲线诸点进行拟合[15]。每个温度应力等级选取1个试件的数据，分别按照线性模型，对数线性模型和幂次模型进行回归拟合，退化轨迹模型的判定系数(R-square)见表2。

表2 几种退化轨迹模型拟合的判定系数

幂次模型的表达式如式(4)所示

y=a*xb+c

(4)

其中：x表示垂向位移量，单位为mm；y表示疲劳载荷次数；a,b,c为模型参数。

从拟合效果可见，幂次模型具有最好的拟合效果。直观上，幂次曲线的特点适合于描述被试橡胶减振器高度变化由快到慢的趋势，如图8所示。

选取幂次模型为寿命特征参数的退化轨迹模型，对16组试验减振器的垂向变形量进行拟合，拟合结果见表3。伪失效寿命是指根据试验数据拟合的产品寿命特征参数退化轨迹模型方程和失效阈值反解出的产品失效寿命，由于该寿命值并非试验所得，故称为伪失效寿命[15]。反解出的减振器伪失效寿命结果如表3所示。

表3 幂次拟合方程及伪失效寿命

3.2 温度加速模型

每个温度等级下有4个样件，对应4个失效寿命值，需使用统计方法使每一温度等级对应一个统一的失效寿命值。由于本试验属于小样本量试验，可选取中位数法作为不同温度等级下的统一失效寿命计算方法[16]，计算结果如表4所示。

表4不同温度应力下减振器统一寿命值

Tab.4Lifeoftherubberisolatorunderdifferenttemperature

温度/℃120896340寿命值4.92×1053.21×1061.36×1076.04×108

将表4中数据代入多种的加速模型进行拟合，发现失效物理中的物体失效反应论模型具有很好的拟合效果。根据反应论模型，反应速度V与温度的关系可用阿伦尼乌斯方程进行描述。

V=Ae-ΔE/RT

(5)

其中：V为反应速度；T为绝对温度，单位为开尔文；A为常数；-ΔE/R也可看作是常数。

进一步推算寿命值与温度的关系，可将式(5)线性化为

lnξ=a+b/T

(6)

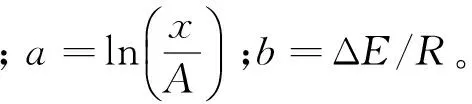
使用方程(6)对表4数据进行拟合，拟合结果如图9所示，图中横坐标为开式温度的倒数，纵坐标对应式(6)左边部分。表4数据的拟合度为0.953 3，拟合得到的被试减振器温度应力加速方程为

lnξ=-14.047+10 540/T

(7)

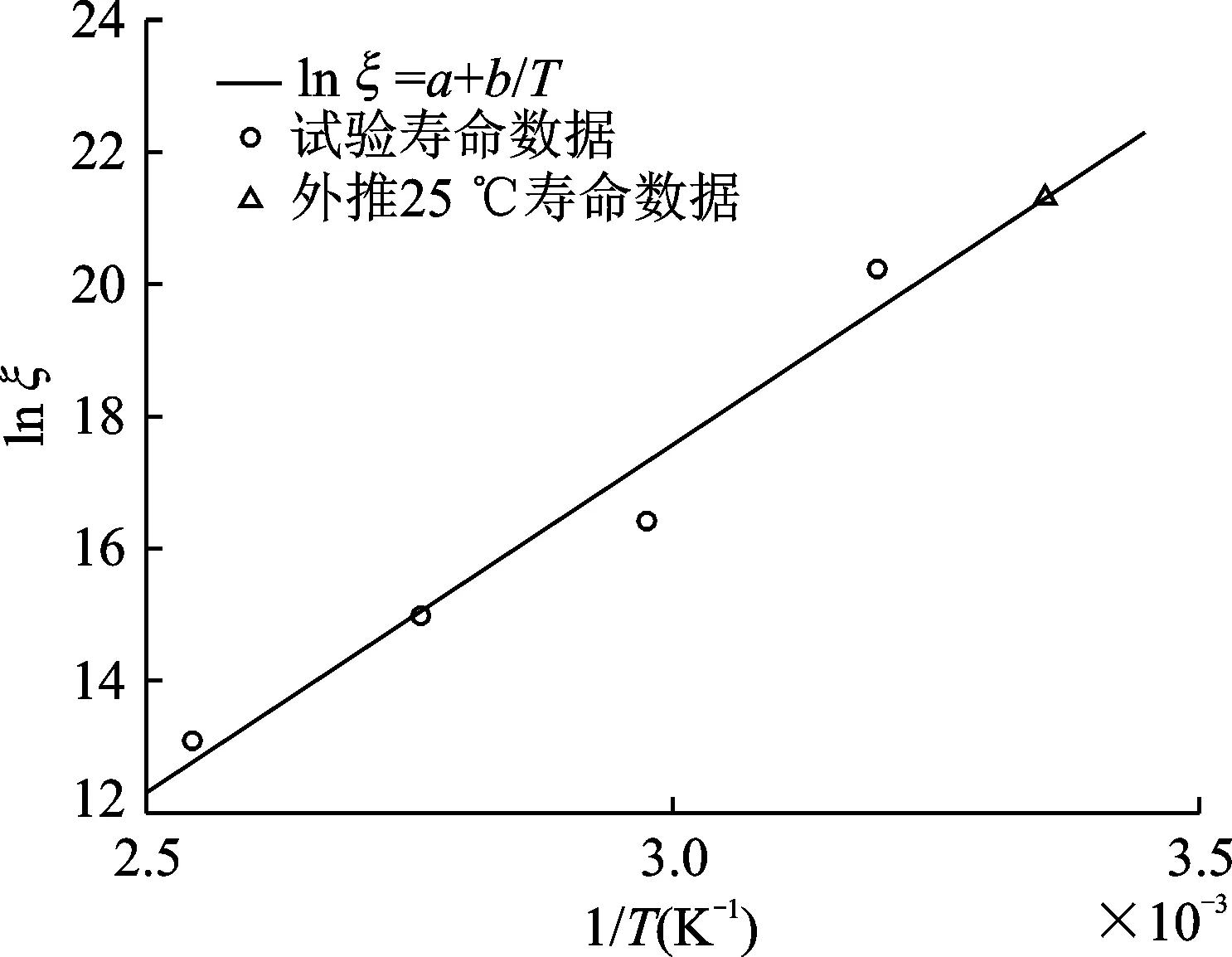
图9 加速方程(6)的拟合结果Fig.9 Fitting result of the acceleration equation (6)

3.3 使用寿命评估

加速方程(7)可作为加速模型描述被试减振器不同温度加速应力下的寿命情况。因此可通过方程(7)，使用外推法计算被试减振器在工作温度条件下的寿命值。

被试减振器的正常使用温度约25 ℃，取对应的绝对温度T=298.15 K代入方程(7)可得减振器的正常使用寿命评估值为1.79×109次循环载荷，如图9所示，换算成时间约为4.73年，与工程应用中该减振器使用寿命的经验结论较为吻合。

4 结束语

针对现有橡胶减振器寿命计算理论的局限性，将橡胶减振器分为寿命周期构型不变类橡胶减振器和寿命周期构型变化类橡胶减振器，笔者指出了后者的主要特点和判别方法，分析了其失效机理和寿命特征参数选取原则，并给出了其寿命评估的方法思路；设计并开展了基于力控制温度应力加速的寿命周期构型变化类橡胶减振器的加速试验，该试验相比传统橡胶制品的加速试验具有试验时间短，数据实时性强，有效数据量大，数据可挖掘性强等优点，适合第二类橡胶减振器的寿命评估研究；给出了基于加速试验数据的被试橡胶减振器寿命评估方法思路，其垂向变形量退化轨迹符合幂次模型，温度应力的加速模型符合反应论模型。通过外推计算的正常温度下的使用寿命与实际使用情况较为吻合。

[1] Li Qian, Zhao Jiancai, Zhao Bo. Fatigue life prediction of a rubber mount based on test of material properties and finite element analysis[J]. Engineering Failure Analysis, 2009, 16(7): 2304-2310.

[2] Woo C, Kim W, Lee S, et al. Fatigue life prediction of vulcanized natural rubber subjected to heat aging[J]. Procedia Engineering, 2009, 1(1): 9-12.

[3] Harbour R J, Fatemi A, Mars W V. Fatigue life analysis and predictions for NR and SBR under variable amplitude and multiaxial loading conditions[J]. International Journal of Fatigue, 2008, 30(7): 1231-1247.

[4] Mars W V, Fatemi A. A literature survey on fatigue analysis approaches for rubber [J]. International Journal of Fatigue, 2002, 24(9): 949-961.

[5] Woo C S, Park H S. Useful lifetime prediction of rubber component[J]. Engineering Failure Analysis, 2011, 18(7): 1645-1651.

[6] 张方，周凌波，姜金辉，等. 基于频域法的随机振动疲劳加速试验设计[J].振动、测试与诊断，2016，36(4)：659-664.

Zhang Fang, Zhou Lingbo, Jiang Jinhui, et al. Random vibration fatigue accelerated test design based on frequency domain methods[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(4): 659-664.(in Chinese)

[7] 王真，赵志高，刘芳.全柔性浮筏隔振系统建模与隔振性能分析[J].振动、测试与诊断，2017，37(1)：70-75.

Wang Zhen, Zhao Zhigao, Liu Fang. Modeling and isolation efficiency analysis for global flexible floating raft isolation system[J].Journal of Vibration, Measurement & Diagnosis, 2017, 37(1): 70-75. (in Chinese)

[8] 朱石坚，何琳. 船舶减振降噪技术与工程设计[M].北京：科学出版社，2002:41-43.

[9] 丁智平，陈吉平，宋传江，等. 橡胶弹性减振元件疲劳裂纹扩展寿命分析[J].机械工程学报，2010，46(22)：58-64.

Ding Zhiping, Chen Jiping, Song Chuanjiang, et al. Analysis of fatigue crack growth life for rubber vibration damper[J]. Journal of Mechanical Engineering, 2010, 46(22): 58-64. (in Chinese)

[10] Saintier N, Cailletaud G, Piques R. Multiaxial fatigue life prediction for a natural rubber [J]. International Journal of Fatigue, 2011, 28(5-6):530-539.

[11] Flamma M, Spreckels J, Steinweger T, et al. Effects of very high loads on fatigue life of NR elastomer materials [J]. International Journal of Fatigue, 2011, 33(9):1189-1198.

[12] Andriyana A, Saintier N, Verron E. Configurational mechanics and critical plane approach concept and application to fatigue failure analysis of rubberlike materials[J]. International Journal of Fatigue, 2010, 32(10): 1627-1638.

[13] 邓爱民. 高可靠长寿命产品可靠性技术研究[D]. 长沙：国防科学技术大学，2006.

[14] Grandcoin J, Boukamel A, Lejeunes S. A micro mechanically based continuum damage model for fatigue life prediction of filled rubbers[J]. International Journal of Solids and Structures, 2014, 51(6): 1274-1286.

[15] Meeker W Q , Escobar L A, Lu C J. Accelerated degradation tests: modeling and analysis[J]. Technometrics, 1998, 40(2): 89-99.

[16] 王小莉. 橡胶隔振器多轴疲劳寿命预测方法研究[D]. 广州：华南理工大学，2014.