基于模糊的框架变形重构的应变测量修正*

潘兴琳， 保 宏， 张旭东

(1.西安电子科技大学电子装备结构教育部重点实验室 西安， 710071) (2.西安电子科技大学信息感知技术协同中心 西安，710071) (3.南京电子技术研究所结构工艺研究部 南京，210039)

引 言

随着智能结构和健康监测的发展，基于应变测量数据的变形重构技术越来越重要[1]。比如嵌入天线的机翼可以通过实时变形监测，给控制和作动系统提供反馈；大型可展开天线准确的变形估计可以有效地提高天线工作性能，因此实现高精度的结构变形重构具有重要意义。

目前基于应变的变形重构研究已有许多。Davis等[2]针对振动悬臂梁的形变估计，通过离散化处理，以若干个函数表示各离散点位移的组成分量，并推导出在相应函数下的应变表达式。根据实际测量的应变量确定各个应变表达式在总体应变中的所占的比重，由此就可以将位移场表示为相应函数的线性组合。但是函数的选取需要对结构和载荷有充分的了解，在实际应用中存在一定难度。Ko等[3]提出非线性位移理论，将弯曲变形的梁分段线性化，每一段内的变形看作受线性变化的弯矩作用而发生的弯曲变形，然后根据经典梁理论[4]推导出每一段内应变的线性表达式，由此推导相应的位移表达式。随后Ko将该理论扩展到结构的形变估计当中，如变截面梁、简支梁、曲梁、翼盒及板[3-5]等。但是非线性位移理论是一种单维方法，在用于三维结构或者复杂结构，为了得到较好的估计精度需要的传感器数目较多，适用性较差。Foss等[6]提出了一种从应变和结构的模态特性来实现结构变形重构的方法。该方法的理论基础是结构的变形位移量可以表示成各阶模态的线性组合，而且应变也存在与此对应的关系。首先根据测量所得应变量与应变模态求出模态坐标，即各阶模态的权重，然后将位移量表示成各阶位移模态的线性组合，建立了应变-位移关系。但是模态信息较难获取，特别是对于有几何非线性结构而言,因此该方法存在一定局限性。

上述研究方法一般需要充分精确的载荷或者材料的弹性惯性信息，而这些数据信息往往难以获取，而且对于复杂结构的变形无法准确的测量。为了满足智能结构和健康监测的要求，算法应该能够适应复杂拓扑结构和边界条件，并且在大范围的载荷或者材料的弹性惯性变化下能够保持准确、稳定、实时。Tessler等[7]提出了一种满足上述要求的逆有限元方法，该方法利用最小二乘变分原则结合测量所得的应变数据来估计任意形式结构的变形情况，包括杆、梁、板、壳及实体，为了完成对任意板壳结构的建模，基于一阶剪切变形理论开发了有3个节点的一个逆壳单元，结构按C°连续的要求离散化，可以适用于任意位置和任意方向安装的传感器所得的数据。Cherlone等[8]对逆有限元方法的应用做了更为深入的研究，说明了该方法的准确性和稳定性以及适用性。因为在iFEM中的方程只用到了应变-位移关系，所以该方法可以在事先不知道结构的材料参数、阻尼特性以及载荷的情况下完成对结构静态和动态响应的估计，而且该方法最终基于一组线性代数方程组来进行求解，计算效率高。

本研究在逆有限元的基础上，推导了框架表面应变与框架测量点变形之间的表达式。针对应变测量过程中由于模型安装和测量操作等因素引入的误差，基于模糊系统的普遍逼近特性[9]，采用自构架模糊网络逼近测量应变量与iFEM求解应变量之间的关系，从而实现对测量应变量的修正。利用框架模型上进行测量验证实验，对该方法的有效性进行了初步验证。

1 建立测量模型

根据Gherlone等[8]提出的逆有限元法，对于任意一段结构可以得到应变-位移的关系表达式

KU=F

(1)

其中：

(2)

所以，对于未知的节点变形，可以通过任意截面应变来求取，U=K-1F。并且对于任一确定的单元，K-1是保持不变的，不随工况的变化而改变。

根据式(2)可以确定任一段内任意点应变与节点位移的关系，对于段内任意一点位移可以通过节点位移和形函数确定

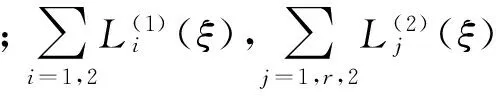
通常U是待求解的位移量，基于测量得到的应变，根据公式U=K-1F，即可确定位移。逆解的过程与上述过程相反，位移量U已知，进而推导得到相应的应变。通过式(1)可以确定末节点位移与应变的关系，再根据式(3)可将任一段内的任意节点位移与应变相对应，逆解出来相应的应变量。

在应用逆有限元法时，由于存在操作误差(包括应变片粘贴工艺、粘贴位移)、系统误差(放大器的零点漂移、仪器的测量误差等)和模型误差(主要包括模型结构本身的连接、分段等)，导致测量应变存在误差。进而根据实验测量应变计算得到的理论位移量与实验测量的位移量存在较大偏差。结构变形重构的精度降低，难以满足实际应用中的精度要求。

2 误差修正

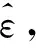
测量应变量中包含了较多不确定的误差因素，因而与逆解应变量之间存在的映射关系难以明确得到，很难设计结构型式固定的模糊网络完成准确的表达。本研究采用自构架模糊网络法，即模糊系统的隶属函数与规则，根据某种机制进行自主增加并调整其分布来完善模糊系统结构，自主构架网络来逼近测量应变量与逆解应变量之间的映射关系。

模糊网络法基于T-S型模糊逻辑系统，采用三角隶属函数。模糊网络构建过程中可以自主增删隶属函数和模糊规则，时刻保持模糊系统精简，同时能够以较高精度逼近不同载荷情况下测量应变量与逆解应变量之间的映射关系。模糊网络法的自构架训练阶段分为4个过程：增加隶属函数和规则；删除隶属函数和规则；自适应规则后件；固化规则库。

2.1 增加隶属函数和规则

根据以下两个准则[10]判断是否需要增加隶属函数。

1) 系统误差准则：以系统的均方根误差(root mean square，简称RMS)来描述系统误差。若系统误差大于一个预先设定的误差阈值Er，则说明当前隶属函数分布不能很好地描述输入和输出之间的关系，需要增加隶属函数。

2)ε完备性：针对输入区间范围内的每一个输入变量都至少存在一个隶属函数，其隶属度不小于一个设定值ε，ε值一般取0.5。找出所有输入变量在当前隶属度函数分布下对应的最大隶属度，如果最大隶属度中的最小值小于ε，则需增加隶属函数。

在增加隶属函数之前，针对每个测量应变输入，需要判断当前测量应变量是否与已有的隶属函数中心点重合，若重合，则只生成规则，而不再增加新的隶属函数。当一个新隶属函数增加时，则以当前该输入应变的值为中心点，相邻隶属函数的中心点分别为左右端点。同时，相邻隶属函数的左右端点也要调整为新增隶属函数的中心，以保持隶属函数的连续分布。在生成规则时，以当前各个应变输入中隶属度最大的隶属函数为规则前件，逆有限元求解的应变量作为规则后件，每次只生成一条规则。假设训练数据中有N个输入x1,x2,…,xN，则模糊规则形式如下。

y=αi

(4)

因此得到在k时刻，该位规则库的输出[11]为

(5)

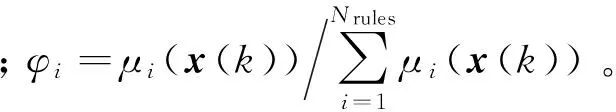
2．2 删除隶属函数和规则

一个自构架模糊系统如果只能增加隶属函数和规则，那么随着训练数据不确定性的增加，规则数的增长则必然导致计算负担的增大和参数学习效率的降低。因此需要删除那些对系统作用可忽略不计的隶属函数和规则，保持系统的精简性。定义规则贡献率Ci为第i条规则的输出占系统总输出的比例，Si为规则的删除指标[12]

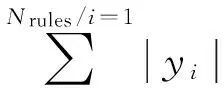
(6)

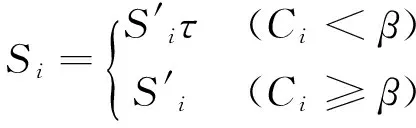
(7)

Si初始化为1，如果Ci小于β，则Si衰减；否则Si保持不变。当Si衰减到低于删除阈值Ω时，则删除该条规则。

2.3 自适应规则后件

基于规则库当前的估算输出值和期望输出值对规则后件进行调整。在当前k时刻，第i条规则后件调整的具体表达式[13]如下

Δαi(k)=γμi(k-1)(r(k-1)-y(k))

(8)

其中：μi(k-1)和r(k-1)分别为在k-1时刻第i条规则的激活度和实测输出值；y(k)为当前k时刻系统的估算输出值；γ为一个常量，其大小直接影响到后件调整的快慢。

2.4 固化规则得到模糊网络

经过多次训练，精度满足指标要求，模糊网络自构架完成。则固化当前规则，保存模糊网络。在应用阶段中，测量应变量输入到训练阶段得到的模糊网络中，经过网络计算直接得到相应的输出作为修正后的应变量。

整个应变测量修正算法可以分为两个阶段，模糊网络训练建立阶段和网络应用实现重构阶段。两个阶段的结构框图如图1，2所示。

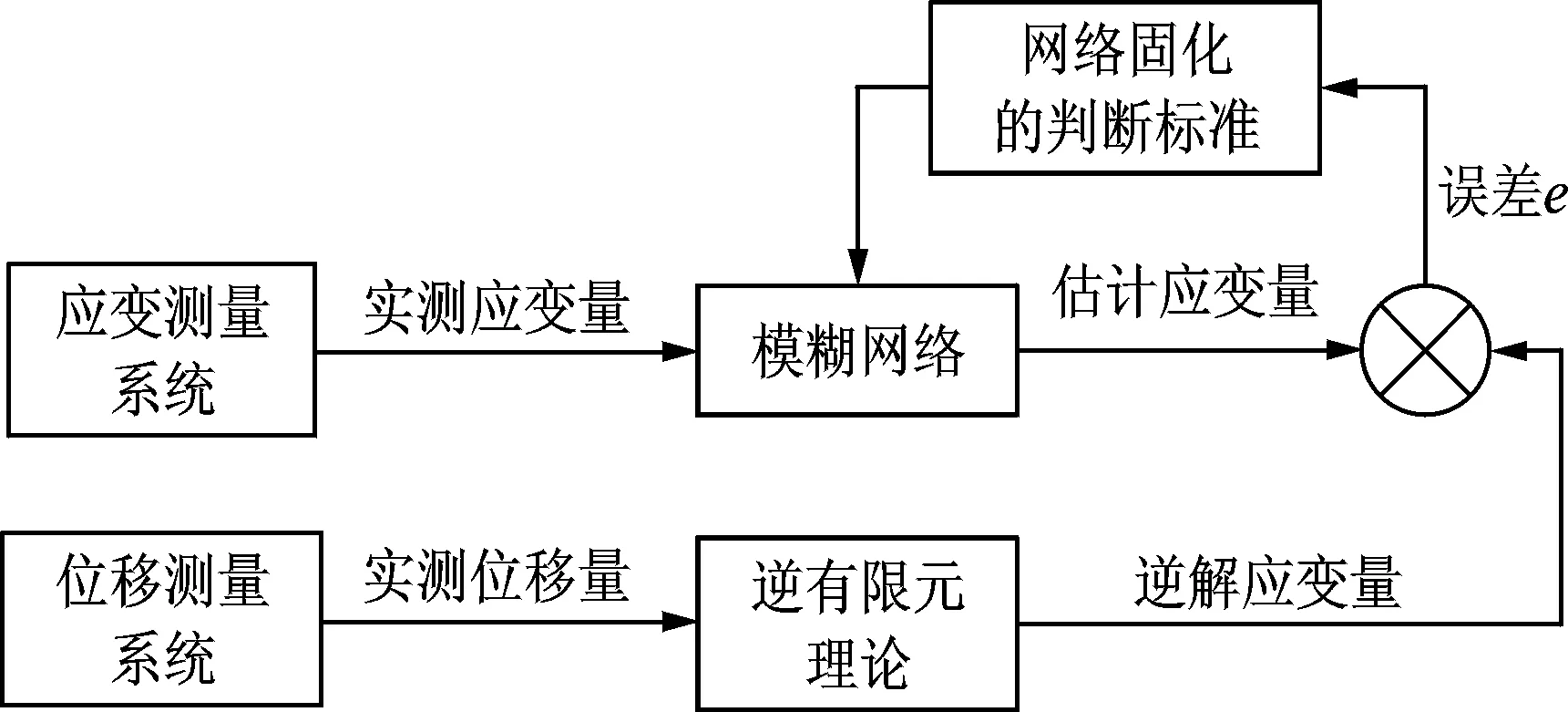
图1 模糊网络训练建立阶段框图Fig.1 The diagram of the fuzzy network training phase

图2 网络应用实现重构阶段框图Fig.2 The diagram of the fuzzy network application phase

3 实验算例

为验证提出的测量应变修正方法在实际应用中的有效性，设计了柔性框架模型静态测量实验。柔性框架的主要组合部分包括：前后缘模块、肋板模块及中间梁模块。单翼展向长2 m，由6个单元拼接而成。框架材料为6061-t6铝，E=73 000 MPa,ν=0.3，ρ=2 712.63 kg/m3。实验过程中分别利用两套测量系统同时测得框架测量点的应变量和位移量。实验测量系统组成如图3中所示。应变测量系统由电阻式全桥应变片、信号放大器以及数据采集卡组成；位移测量系统由动态三维光学测量仪(NDI Optrotrak Certus)及配套软件组成。

图3 实验框架模型及测量系统结构Fig.3 Structure of framework and experimental measurement system

为了完成逆有限元法的验证实验，将应变测量点布置在各段中间梁的中间位置，以x轴为中性轴，均布3个与x轴方向相同的测量点，同时在同一位置增加与x轴呈45°方向的3个测量点，选点形式如图4(a)所示，即一个测量点位置布置6个应变片。对于位移测点将其布置在各段中间梁的末端和段内任意一点，6段共布置12个位移测量点。位移测量点分布如图4(b)所示。

图4 应变及位移测量点分布Fig.4 The distribution of strain and displacement measurement points

实验过程中，在框架末端施加单点集中载荷作用，在0～7.5 kg载荷范围逐次增加，共进行20组工况实验。随机选取工况2、工况5、工况7、工况10、工况11、工况15及工况18为测试数据，其余工况为训练数据构建模糊网络。基于逆有限元法得到的应变-位移关系，通过测量的位移量求解得到相应的逆解应变量，以第1段与x方向相同的应变为例，逆解应变与实际应变结果如表1所示。在得到逆解应变的基础上，通过模糊网络建立相关实际应变与逆解应变之间的关系。

表1 模糊网络训练数据

随机选取7组工况数据进行测试，得到经模糊网络修正之后的应变结果如表2所示。代入模糊网络修正后应变所得到的变形重构结果，如表3所示。

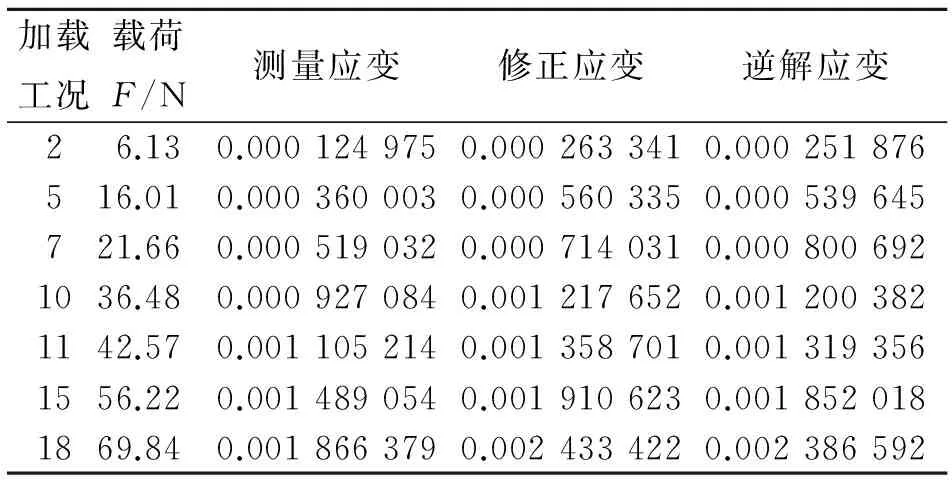
表2 模糊网络测试结果

表3 测量应变修正前后误差比较

Tab.3 The comparision of deformation displacement results

加载工况最大位移/mm修正前RMS/mm修正后RMS/mm误差减小百分比/%210.240.710.2564.79530.773.181.0666.66735.065.411.5970.611079.647.622.2570.471194.779.162.8668.7715126.4510.963.1671.1718157.3712.874.4465.55

RMS为均方根误差(root-mean-squared error,简称RMS)

经过应用模糊网络建立关系进行修正，修正后代入求解变形位移量。RMS较修正之前明显下降，在工况15下，误差减小比例最大，达到71.17%。在工况2下，误差减小最小，但是也达到了64.79%。柔性框架实验应用结果表明，笔者提出的测量应变修正方法能够很好的提高测量精度，具有良好的实用性。

4 结束语

针对三维框架弹性变形重构问题，笔者提出了一种应变测量修正方法。在三维框架模型上进行测量实验。实验结果显示,经过模糊网络修正之后，基于修正后应变数据实现结构变形重构误差大幅度降低，验证了该应变测量修正方法在三维框架变形重构中的可行性与可靠性。后续的工作将主要对传感器的优化，包括数量上和测点位置的优化，能够更加精确地完成空间结构的变形重构。

[1] 袁慎芳. 结构健康监控[M]. 北京:国防工业出版社, 2007: 206-212.

[2] Davis M A, Kersey A D. Shape and vibration mode sensing using a fiber optic bragg grating array [J]. Smart Materials and Structures, 1996, 6(5):759-765.

[3] Ko W L, Fleischer V T. Extension of Ko straight-beam displacement theory to deformed shape predictions of slender curved structures[R]. California：NASA, 2011.

[4] Timoshenko S P. On the correction for shear of differential equations for transverse vibrations of prismatic bars [J]. Philosophical Magazine, 1921, 245(41): 744-746.

[5] Jutte C V, Ko W L, Stephens C A, et al. Deformed shape calculation of a full-scale wing using fiber optic strain data from a ground loads test[R]. California: NASA, 2011.

[6] Foss G C, Haugse E D. Using modal test results to develop strain to displacement transformations [C]∥Proceedings of the 13th International Modal Analysis Conference. Washington,USA:The International Society for Optical Engineering, 1995, 2460: 112-128.

[7] Tessler A, Spangler J L. A variational principle for reconstruction of elastic deformations in shear deformable plates and shells [R]. California: NASA CASI (301) 621-0390, 2003.

[8] Gherlone M, Cerracchio P, Mattone M, et al. Shape sensing of 3D frame structures using an inverse finite element method[J]. International Journal of Solids and Structures, 2012,49(22):3100-3112.

[9] Castro J L. Fuzzy logic controllers are universal approximators [J]. IEEE Transactions on Systems, Man and Cybernetics, 1995, 25(4):629-635.

[10] 张涛, 保宏, 杜敬利, 等. 非仿射非线性系统的自主构架模糊控制器[J]. 控制与决策, 2014, 29(8):1532-1536.

Zhang Tao, Bao Hong, Du Jingli, et al. Self-structuring fuzzy controller for nonaffine nonlinear system[J]. Control and Decision , 2014, 29(8):1532-1536. (in Chinese)

[11] Phan P A, Gale T J. Direct adaptive fuzzy control with a self-structuring algorithm[J]. Fuzzy Sets and Systems, 2008, 159(8):871-899.

[12] Pomares H, Rojas I, Gonzalez J, et al. Structure identification in complete rule-based fuzzy systems [J]. IEEE Transactions on Fuzzy Systems, 2002, 10(3): 349-359.

[13] Chen Pincheng, Wang Chihsu, Lee T. Robust adaptive self-structuring fuzzy control design for non-affine nonlinear systems[J]. International Journal of Systems Science, 2011,42(1):149-169.