基于Matlab与DMC的工业机器人轨迹规划研究与实现
乐 英,库 巍,董志聪,陈亚亮
(华北电力大学 能源动力与机械工程学院,河北 保定 071000)
轨迹规划是机器人运动学的具体应用,它的目的是根据任务要求计算出预期的运动轨迹,从而对机器人的任务、轨迹等进行描述[1].常用的机器人轨迹规划分为笛卡尔空间轨迹规划和关节角度空间轨迹规划.在关节角度空间规划中通常给出起始点,运动轨迹上的中间点是通过插值来进行求取的.具体的过程是在关节空间中描述各作业点的位姿,然后在插补点的基础上拟合成光滑的函数.由于各关节函数描述了各关节所经过的点,机器人在联动的情况下,各关节通过各自轨迹段的时间是相同的,所以它们在满足各自的期望位姿之外同时达到轨迹段的终点.机器人的轨迹规划方法主要是利用多项式、样条曲线以及结合几种不同的曲线来对关节进行规划[2].在实际工程应用中,大多采用三次多项式[3].文献[4]采用Matlab机器人工具箱建立机器人三维仿真模型对其进行仿真,但是可视感不强,而且对机器人规划的轨迹不够直观.针对这些问题,本文通过用Matlab的图形用户界面(Graphical User Interface,GUI)工具编写6自由度机器人的仿真界面.
机器人控制系统是机器人运动学的核心内容,它越来越多地使用开放式结构,DMC是美国GALIL公司的产品.与其他运动控制器相比,DMC具有产品繁多、价格便宜、使用简单等特点[5].DMC-21x/21x3系列是GALIL经济型多轴独立控制器,该控制器提供了强大的功能.与早期型号相比,除了更高的通信速度与编码器反馈速度外,提供的选件更丰富.DMC-21x/21x3是为解决复杂运动问题而设计的,它能包括点动、点到点定位、矢量定位、电子齿轮同步、电子凸轮、轨迹运动等[6].此外,控制器能够对运动规划曲线进行平滑处理,可很大程度地减少对机械部分的运动冲击.
本文主要在Matlab编写的仿真平台上,对6自由度工业机器人进行轨迹规划,然后研究三次多项式轨迹规划算法及其在DMC运动控制器上的具体实现方式.首先以实验室深圳元创兴REBOT-V-6R机器人为研究对象,用Matlab建立6自由度工业机器人仿真平台,在该平台上对机器人规划矩形轨迹,并得到笛卡尔空间的轨迹图、各关节角位移、角速度和角加速度的变化图;然后将6个关节的角度变量输入到C++编程的控制平台上;最后通过该控制平台控制实验室的实体机器人,验证本文所研究的轨迹规划算法的可行性和可靠性.
1 在Matlab仿真软件上进行轨迹规划实验与分析
1.1 仿真界面的生成
以实验室的机器人为研究对象,通过用Matlab编写三维实体函数建立机器人三维实体模型;然后利用guide函数,在弹出的向导选项中选择一个空的选项,进入一个编辑界面,为了满足一些特殊的命令要求,在界面中添加一些必要的功能控件,在对应的控件下编写各自的回调函数后,就能得到机器人的仿真界面.
由于Matlab中没有三维实体函数,为了建立与实体机器人相似的模型,需要编写三维实体函数,其中空心的长方体单元函数部分代码如下:
function h =changfangti(c,k,g,px,py,pz,cl)
%c,k,g为长方体长宽高,px,py,pz为3个方向的偏移量,cl为长方体的颜色设置.
[X1,Y1]=meshgrid(-c/2:0.1:c/2,-k/2:0.1:k/2);%生成x,y坐标
h1=surf(X1+px,Y1+py,zeros(size(X1,1),size(X1,2))+ pz,′FaceColor′,cl,′LineStyle′,′none′);hold on
h2 = surf(X1+px,Y1+py,zeros(size(X1,1),size(X1,2))+pz+g,′FaceColor′,cl,′LineStyle′,′none′);hold on
……
[X32,Y32]=meshgrid(-g+c/2:0.1:c/2,-k/2:0.1:k/2);
h6=surf(X32+px,Y32+py,zeros(size(X32,1),size(X32,2))+pz,′FaceColor′,cl,′LineStyle′,′none′);hold on
rotate(h6,[0 1 0],90,[px+c/2,py,pz]);
h=[h1 h2 h3 h4 h5 h6];
为了增强机器人模型的可视感,还需要编写空心圆柱等函数.通过用Matlab的GUI编写6自由度工业机器人的仿真界面,如图1所示.
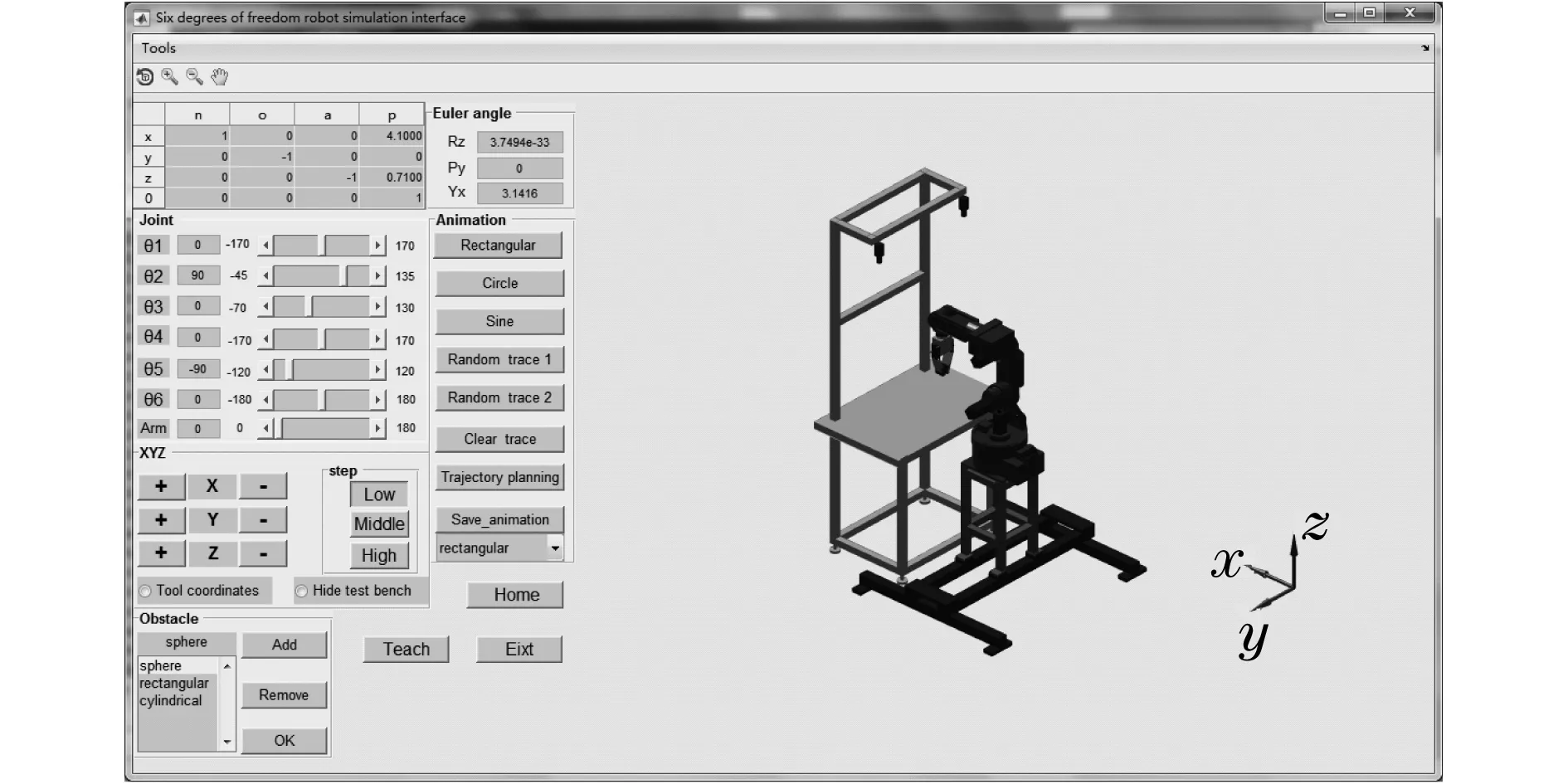
图1 6自由度机器人仿真平台Fig.1 Six degrees of freedom robot simulation platform
1.2 轨迹规划
采用三次多项式在关节空间对机器人轨迹进行规划.根据已知的工作空间原始路径点,利用编写的机器人运动学算法,反求出关节空间中各关节对应的角位移值[7].再根据各种规划方法中具体的求解算法,求出相应的速度、加速度值,从而得到各关节轨迹曲线,以对机器人的轨迹进行规划.
三次多项式样条中,两节点之间的曲线段是由三次多项式拟合生成.三次多项式表达式中共有4个未知系数(a0,a1,a2,a3),对其求一阶、二阶导,可求出机器人末端关于时间t的速度、加速度的函数式[8]:
其中与始末时间点t0,tf对应的角位移θ0和θf为已知,且满足条件
θ(0)=θ0,θ(tf)=θf
(4)
在每段多项式始末两点处满足二阶连续,设置始末点的速度、加速度,且满足条件[9]
(5)
每个点的角位移值已知,设定其角速度和角加速度为一常数,两点共可得到4个已知条件.将已知条件代入式(1)~(3)中并联立求解,可解出全部未知的系数.
在机器人仿真平台上用三次多项式模拟机器人末端执行机构规划一个矩形轨迹,然后得到机器人6个关节的角度.点击“Rectangular”按钮,仿真平台中的机器人开始运动,具体如图2所示.
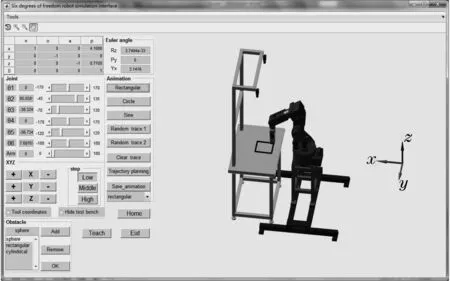
图2 规划一个矩形的仿真图Fig.2 Plan a rectangle of simulation
此时得到机器人前3个关节在[4.5 s,5.5 s]的运动曲线分别如图3所示.

图3 截取的三次多项式规划1~3关节运动曲线Fig.3 The three polynomials are planned for the1~3 joint motion curve
2 机器人轨迹规划DMC验证
DMC-21x/21x3为用户提供了100多条指令用于运动控制和参数设置,而且这些指令能以ASCII码或者二进制码发送.它的大部分命令指令都是两字符命令,并提供了在多种环境下(如Visual Basic,C,C++等)开发的工具软件,可以与DOS,QNX,Windows,Linux相兼容.机器人控制系统软件以Visual Studio 2015集成开发环境为平台,结合Microsoft的基本类库(MFC),基于Windows XP操作系统开发的[10],采用C++语言进行编程,包括编写机器人运动学算法、连接控制器等操作.另外,嵌入GALIL公司提供的动态链接库DMCWin3,它可以建立操作系统与DMC 控制器之间的通信,在对机器人末端轨迹进行规划的过程中,在已经搭建好的6自由度机器人控制平台上,对机器人规划矩形轨迹.
将图2的矩形轨迹规划中的机器人6个关节的角度变量转换对应关节的脉冲数,各关节的运动协调控制由 DMC多维直线插补模式完成.
部分关键代码如下:
m_DMCWin.Command("LMABCDEF ",,szResponse,sizeof(szResponse));
…
m_DMCWin.Command("LE ",,szResponse,sizeof(szResponse));
m_DMCWin.Command("VA5000,5000,5000,5000,5000,5000 ",szResponse,sizeof(szResponse));
m_DMCWin.Command("VD5000,5000,5000,5000,5000,5000 ",szResponse,sizeof(szResponse));
m_DMCWin.Command("BGS ",szResponse,sizeof(szResponse));
得到6自由度机器人控制平台如图4所示.
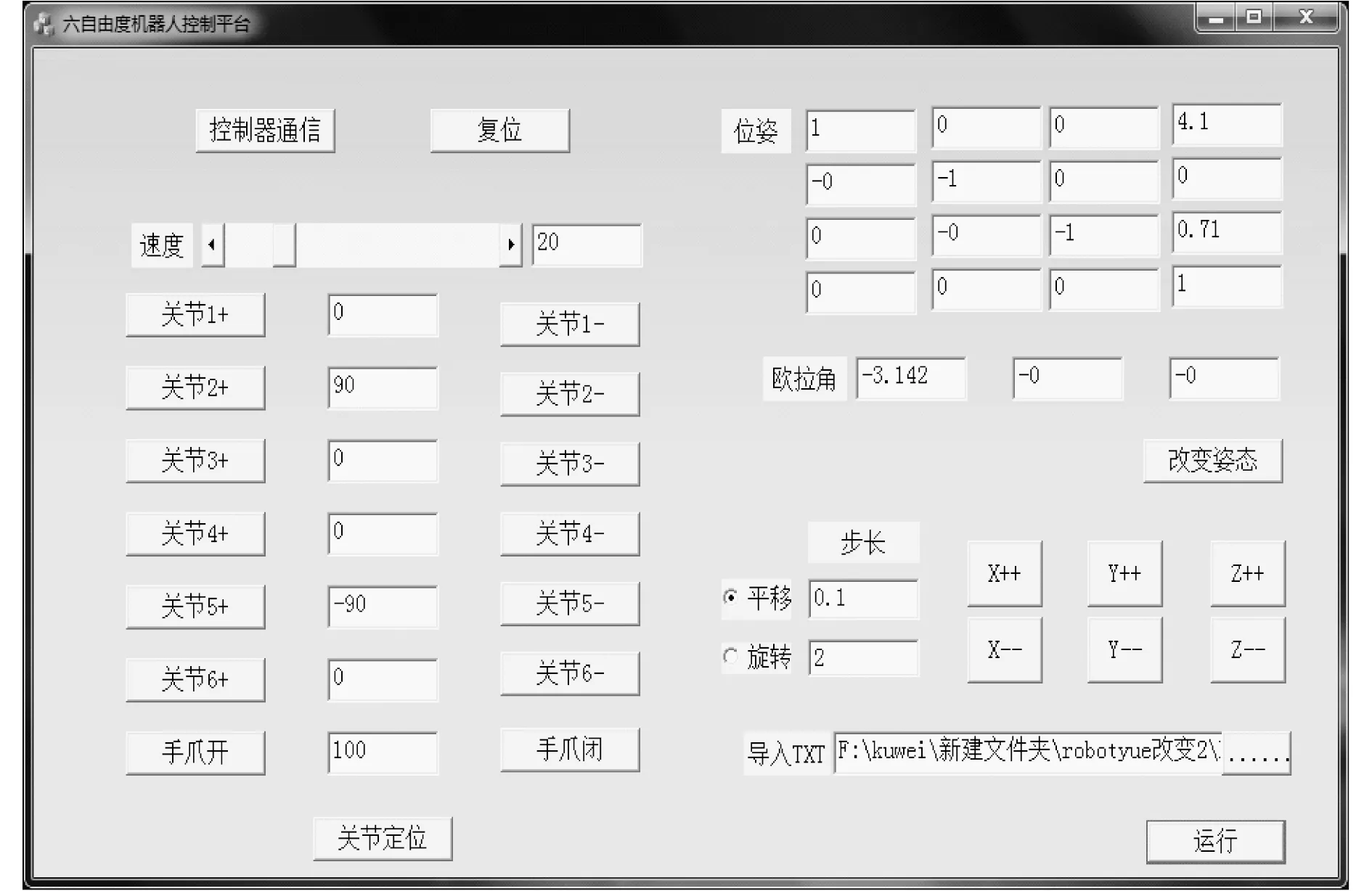
图4 6自由度机器人控制平台Fig.4 Six degrees of freedom robot control platform
将保存的6个关节的脉冲数以文本的形式导入到控制平台,点击运行按钮后,得到机器人实体的仿真轨迹,如图5所示.
从图5中可以看出,根据上述规划方法,实体机器人能够得到与图2仿真平台中一样的矩形轨迹,仿真结果得到了验证.

图5 机器人实体规划一个矩形的仿真图Fig.5 The robot entity plans a rectangular simulation
3 结论
本文用Matlab建立6自由度机器人仿真界面,在仿真界面上,采用三次多项式对机器人末端规划一个矩形轨迹,得到机器人6个关节的运动曲线.在此基础上,采用基于DMC的开放式运动控制系统的6自由度机器人轨迹插补算法,采用C++语言实现上述算法,在已经搭建好的6自由度机器人平台上运行.实验结果表明,机器人末端手爪能在笛卡尔空间精确行走矩形轨迹,运动轨迹连续平滑,证明了文中所采用DMC运动控制器的运动模式方案能精确、可靠地实现关节型机器人的轨迹规划运动.实验结果达到了预期要求.
参考文献:
[1] 孙亮,马江,阮晓钢.6自由度机械臂轨迹规划与仿真研究[J].控制工程,2010(3):388-392.
SUN L,MA J,RUAN X G.Six degrees of freedom of manipulator track planning and simulation[J].Control Engineering,2010(3):388-392.
[2] 朱世强,刘松国,王宣银,等.机械手时间最优脉动连续轨迹规划算法[J].机械工程学报,2010,46(3):47-52.
ZHU S Q,LIU S G,WANG X Y,et al.The optimal pulsating trajectory planning algorithm for manipulator time[J].Journal of Mechanical Engineering,2010,46(3):47-52.
[3] 王学林,邢仁鹏,肖永飞,等.机械臂途经N路径点的连续轨迹插补算法研究[J].组合机床与自动化加工技术,2014(11):92-96.
WANG X L,XING R P,XIAO Y F,et al.The mechanical arm is studied by the continuous trajectory interpolation algorithm ofNpath points[J].Combination Machine Tool and Automatic Processing Technology,2014(11):92-96.
[4] 张舒曼,周亚军.基于Matlab的机器人运动学分析与轨迹规划仿真[J].工业控制计算机,2014(8):12-14.
ZHANG S M,ZHOU Y J.Matlab based robot kinematics analysis and trajectory planning simulation[J].Industrial Control Computer,2014(8):12-14.
[5] 王国栋,王刚,肖聚亮,等.DMC及其在开放式机器人控制器中的应用[J].机床与液压,2003(6):207-209.
WANG G D,WANG G,XIAO J L,et al.DMC and its application in open robot controller[J].Machine Tool and Hydraulic,2003(6):207-209.
[6] 王谦.基于DMC的机器人轨迹规划研究与实现[J].工业仪表与自动化装置,2011(3):86-88.
WANG Q.Based on DMC’s robot trajectory planning research and implementation[J].Industrial Instruments and Automation Devices,2011(3):86-88.
[7] 任志贵,陈进,贺康生,等.基于运动学分析的挖掘机器人轨迹规划新方法[J].中国工程机械学报,2012,10(2):150-155.
REN Z G,CHEN J,HE K S,et al.Based on kinematics analysis,a new method of tracking robot trajectory is proposed[J].Chinese Journal of Construction Machinery,2012,10(2):150-155.
[8] 林仕高,刘晓麟,欧元贤.机械手笛卡尔空间轨迹规划研究[J].机械设计与制造,2013(3):49-52.
LIN S G,LIU X L,OU Y X.Cartesian space trajectory planning study[J].Mechanical Design and Manufacturing,2013(3):49-52.
[9] 徐海黎,解祥荣,庄健,等.工业机器人的最优时间与最优能量轨迹规划[J].机械工程学报,2010(9):19-25.
XU H L,XIE X R,ZHUANG J,et al.Optimal time and optimal energy trajectory planning for industrial robots[J].Journal of Mechanical Engineering,2010(9):19-25.
[10] 胡绳荪,王明建,申俊琦,等.J形坡口焊接机器人运动控制系统设计[J].天津大学学报(自然科学与工程技术版),2014,47(4):371-376.
HU Y S,WANG M J,SHEN J Q,et al.J-groove welding robot movement control system design[J].Journal of Tianjin University(Natural Science and Engineering),2014,47(4):371-376.

