基于改进BP神经网络优化的牛头刨床动力学仿真

王 莹,许洋洋,薛东彬

(1.郑州工业应用技术学院 机电工程学院,郑州 451150; 2.河南工业大学 机电工程学院,郑州 450007)

牛头刨床在运动过程中,刨头作直线往复运动是主要运动[1].此运动行程分为两个阶段:① 刨头切削工件的进给运动;② 刨头切完工件的回程运动.牛头刨床的刨头速度若控制不当,不仅影响工件的质量,而且会降低工作效率[2].因此,必须对牛头刨床六杆机构进行优化,尽可能保证刨头速度平稳切削和快速返程,从而提高工件产品的质量和效率.

为了改善牛头刨床刨头的切削速度,以往许多研究人员对其进行了大量研究.文献[3]采用Matlab/GUI优化牛头刨床运动参数尺寸,并且对优化结果进行了仿真.以提高工作效率为目标函数,建立了牛头刨床机构行程比的数学模型,采用Matlab/GUI和C语言程序对优化结果进行仿真验证.仿真结果显示,牛头刨床空行程时间减少了32%.文献[4]采用动力学软件ADAMS对优化后的牛头刨床进行动力学仿真研究,建立了刨头速度目标函数,添加了约束条件,采用Matlab软件对其进行优化,得出最优杆长.优化后的牛头刨床刨头切削速度更加平稳,加速度峰值得到了降低.文献[5]研究了牛头刨床刨头的运动精度,探讨了不完全概率信息牛头刨床刨头稳健设计问题.分析了六杆机构运动的几何约束条件,推导出运动产生的误差方程式,根据牛头刨床运动极限方程式设计稳健模型,从而快速得出牛头刨床的最优设计参数.以往研究的牛头刨床机构,很难保证在提高效率的前提下降低加速度峰值.对此,本文采用了改进BP神经网络对牛头刨床机构进行了优化和动力学仿真验证.根据平面坐标系推导出刨头的速度和加速度方程式,确定了六杆机构运动参数变量,构造了优化目标函数,采取改进BP神经网络优化六杆机构的参数变量,将优化结果输入到Solidworks软件中进行了动力学仿真,为牛头刨床机构的动力学研究提供了参考依据.

1 牛头刨床运动分析

牛头刨床连杆机构运动简图如图1所示,运动过程如下:电机带动曲柄OA旋转,连接滑块A将运动传递给摆动导杆BD做往复摆动,通过连杆BC带动刨头C做往复切削运动.

图1 六杆机构简图Fig.1 Diagram of six bar mechanism

六杆机构构件在坐标轴上投影关系式[6]如下:

式中:θ1为曲柄OA的转角;θ2为摆动杆BD的转角;θ3为连杆BC与水平的夹角;rOA为曲柄OA的长度;rOD为机架OD的长度;rAD为滑块A到点D的长度;rBD为摆动杆BD的长度;rBC为连杆BD的长度;rCE为刨头运动的位移.

θ2和θ3的关系式如下:

(3)

θ3=π-arctan[(rDE-rBDsinθ3)/rBC]

(4)

将θ3对时间求导得

(5)

式中:ωOA为曲柄OA的角速度.

将rCE对时间求导得

(6)

(7)

式中:

2 六杆机构参数优化

2.1 确定设计变量

牛头刨床六杆机构的运动主要体现在刨头的切削运动,而刨头的位移、速度和加速度由设计参数rOA,rBD,rBC,rOD,rDE和φ决定.因为牛头刨床在工作过程中,摆动杆、连杆和连杆决定压力角的值.当刨头运动到摆动杆的摆动角平分线时,压力角较小,此时rDE=rBD[1+cos(φ/2)]/2,所以,rDE不是独立变量.由运动学可知,机架rOD=rOA/sin(φ/2),因此,rOD不是独立变量.摆动角与行程速比关系式为φ=180(k-1)/(k+1),k是急回特性参数.因此,牛头刨床六杆机构最终优化设计变量为

X=[rBD,rBC,k]

(10)

2.2 优化目标函数

牛头刨床在切削运动过程中,既要工作行程切削速度保持平稳,又要返回行程具有急回特性.但是两者是矛盾的,通常是在保证工作行程切削速度平稳的条件下,再考虑机构的急回特性.因此,优化目标函数是六杆机构工作行程的速度尽可能保持匀速.根据式(6)可知,刨头的切削速度[7]为

(11)

因此,优化的目标函数为

(12)

式中:vm为理想刨头切削速度;n为曲柄OA转角的等份;θ1i为第i个等份点曲柄OA的转角;v(X,θ1i)为曲柄OA转角为i时刨头实际切削速度.

2.3 添加约束条件

(1) 由六杆机构摆动杆运动分析可知,杆长rBD必须大于rOA+rOD,但是rBD如果太长,就会导致机构重心上升.因此,rBD满足以下条件[8]:

1.1[1+1/sin(φ/2)]≤rBD≤1.8[1+1/sin(φ/2)]

即

g(1)=rBD-1.1[1+1/sin(φ/2)]≥0

(13)

g(2)=1.8[1+1/sin(φ/2)]-rBD≥0

(14)

(2) 连杆rBC越长,六杆机构的最大压力角就会变小,导致机构传动角变大,对于六杆机构的传动性能越好.但是rBC越长,就会使六杆机构空间很大.因此,rBC满足条件[9]:1≤rBC≤2,即

g(3)=rBC-1≥0

(15)

g(4)=2-rBC≥0

(16)

(3) 行程比越大,牛头刨床急回特性越好,工作行程时间越长,对于加工切削越有利.但是行程比越大,导致机构产生惯性力越大.因此,k值的取值范围满足条件[10]:1.2≤k≤2.2,即

g(5)=k-1.2≥0

(17)

g(6)=2.2-k≥0

(18)

3 改进BP神经网络优化

3.1 BP神经网络

BP神经网络是一种多层前馈神经网络,主要是采用误差反向传播算法训练的.BP神经网络包括输入层、隐含层和输出层3个部分,相邻层的神经元是全部连接的,而每一层神经元之间是不连接的,如图2所示.

BP神经网络学习过程采取修正权值以降低误差,根据梯度下降法,连接权值修正公式[11]如下:

(19)

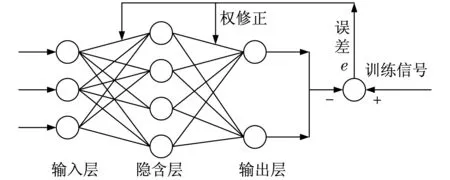
图2 BP神经网络示意图Fig.2 Sketch of BP neural networks

式中:η为学习因子;Ek为第k个样本误差.

权重调整公式如下:

(20)

式中:t为训练次数.

BP神经网络寻优能力较强,但是也存在两个缺点:① 每次训练的次数和最终权值都不相同,网络寻优结果不是唯一值,陷入局部极小值;② 当输入节点较多时,初始权值的随机性导致训练次数增多,收敛速度慢.针对此问题,本文采用粒子群算法改善BP神经网络训练次数,从而跳出局部最小值,以达到优化BP神经网络的目的.

3.2 粒子群算法

粒子群优化算法采取模拟鸟类觅食在N维空间中移动粒子寻找最优解,粒子移动的速度和位置计算公式[12]如下:

(21)

(22)

惯性权重ω较大时,全局搜索能力较强;ω较小时,局部搜索能力较强.为了更好地平衡两者关系,采用如下线性迭代方式:

(23)

式中:ωmax为初始权重;ωmin为最终权重;n为当前迭代数;N为最大迭代数.

这种线性迭代方式中的ω不能更好地适应非线性优化问题.本文采用动态改变惯性权重的粒子群算法，采用如下两个变量公式:

粒子进化度

(24)

粒子聚合度

(25)

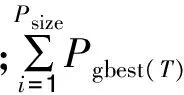
e越小,进化速度越快;e越大,进化速度越慢.当粒子群经过多次迭代后,e值保持为1,说明已经寻找到最优值.α越小,粒子群中粒子分布越分散,不容易陷入局部最优值;α越大,粒子群中粒子分布越集中,容易陷入局部最优值.因此,可以通过惯性权重ω来提高进化速度和全局搜索最优能力:

ω=ω0-0.5e+0.1α

(26)

式中:ω0为ω的初始值.

3.3 粒子群优化BP神经网络

在改进BP神经网络优化中,粒子适应度为

(27)

式中:n为随机训练样本个数;c为网络神经元输出个数;Yij为第i个样本第j个理论输出值;yij为第i个样本第j个实际输出值.

本文采用改进BP神经网络优化算法对牛头刨床六杆机构目标函数进行优化,计算参数选择如下:输入层和隐含层神经元个数都为9,输出层神经元个数为2,初始种群数量为500,种群最大迭代次数为2000,学习因子c1=c2=2,惯性权重初始值ω0=0.9.优化前与优化后牛头刨床六杆机构几何参数如表1所示.

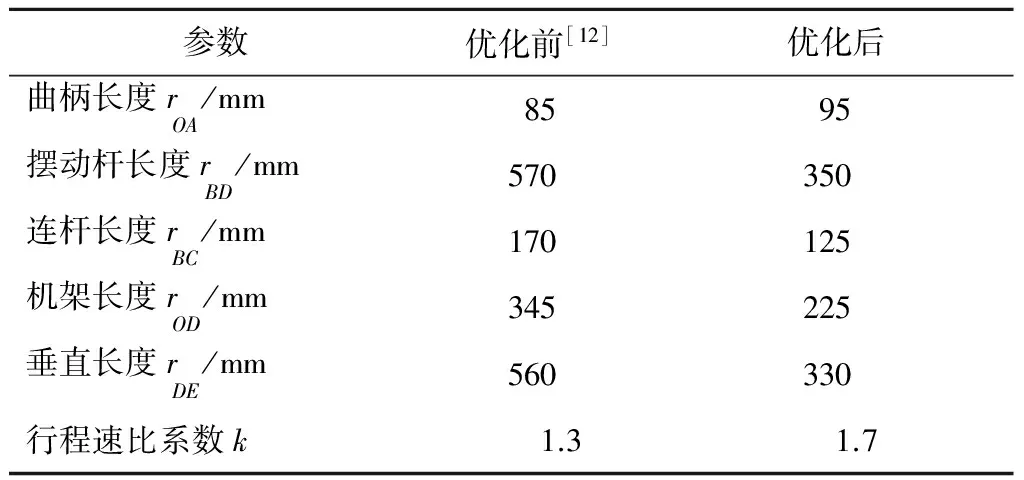
表1 六杆机构优化参数Tab.1 Optimization parameters of six bar mechanism

4 运动仿真及分析

根据优化后的参数,在三维软件Solidworks中创建三维模型,然后进行装配,添加约束条件,并且进行动力学仿真,如图3所示.曲柄OA转速为2π/s,运动时间为1 s.刨头的位移、速度和加速度仿真结果分别如图4、图5和图6所示.

图3 牛头刨床机构三维图Fig.3 3D view of the shaper mechanisms

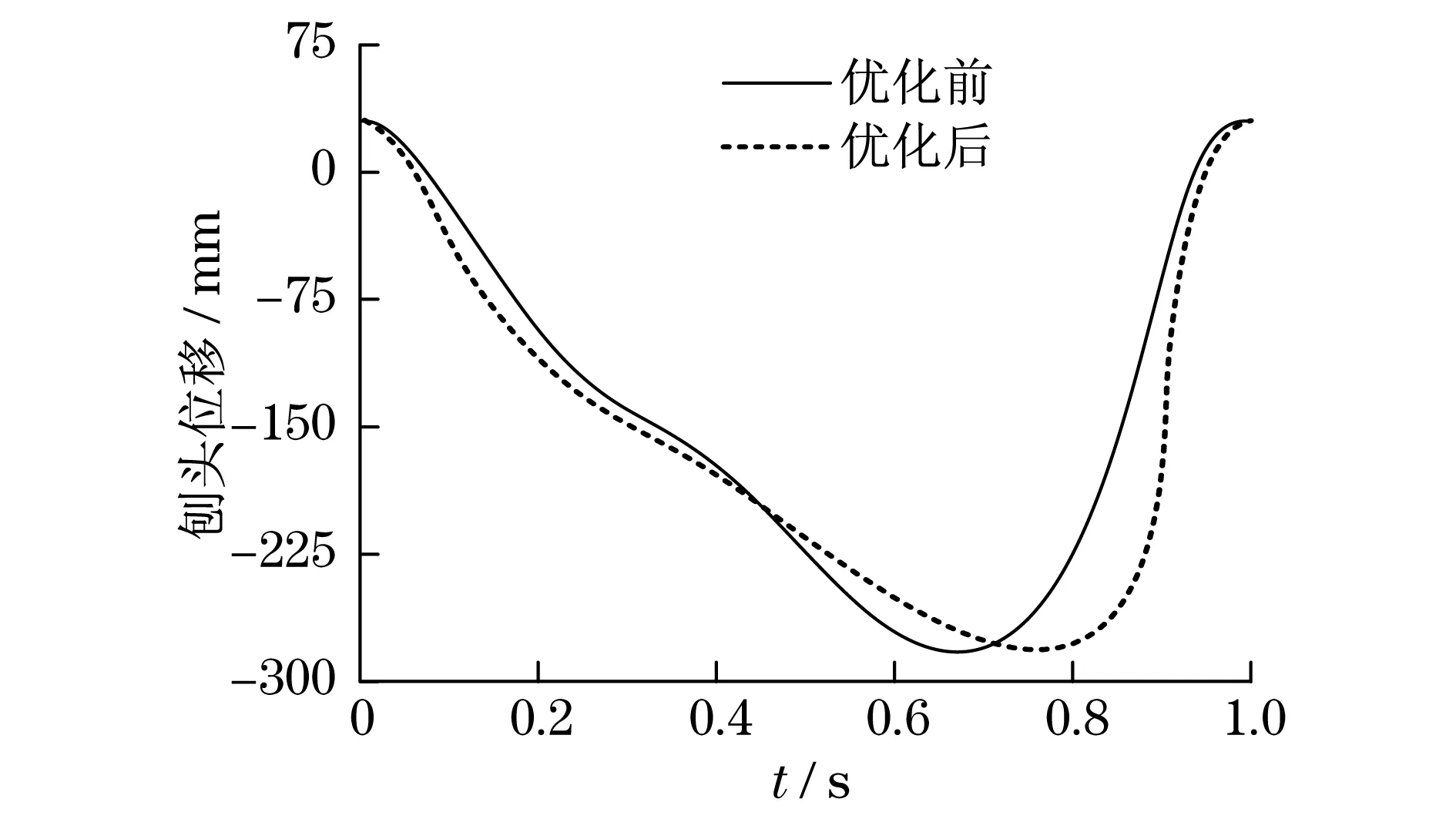
图4 刨头位移仿真结果Fig.4 Displacement simulation of the plow head

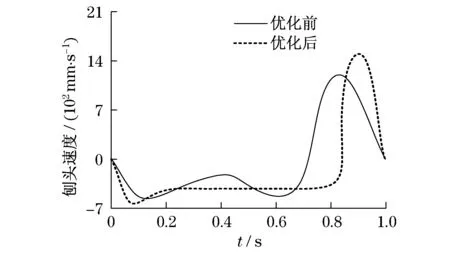
图5 刨头速度仿真结果Fig.5 Velocity simulation of the plow head

由图4、图5和图6的仿真结果可知:优化前刨头运动的工作行程时间范围为0.3～0.7 s,工作行程内速度和加速度峰值分别为550 mm/s和8 000 mm /s2;采用改进粒子群优化后的刨头运动的工作行程时间范围为0.3～0.8 s,工作行程内速度和加速度峰值分别为420 mm/s和0 mm/s2.因此,与优化前相比,优化后的牛头刨床六杆机构,不仅工作行程内刨头速度和加速度峰值降低,运动比较平稳,而且工作行程时间延长,提高了工作效率.

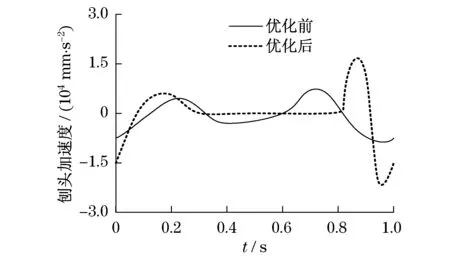
图6 刨头加速度仿真结果Fig.6 Acceleration simulation of the plow head

5 结语

本文研究牛头刨床刨头的动力学,建立牛头刨床刨头的运动方程式.确定优化设计参数变量,构造优化目标函数并且添加约束条件.采取改进BP神经网络对目标函数进行优化.根据优化后的参数创建三维模型,导入到Solidworks软件中进行动力学仿真,并且与优化前的仿真结果进行对比和分析.仿真结果显示,优化后的牛头刨床刨头在工作行程内(0.3～0.8 s)的速度和加速度峰值降低,上下振动幅度减弱,刨头运动比较平稳.同时,在一个工作周期内,工作行程时间延长,提高了工作效率.

参考文献:

[1] 吕鲲,袁扬,郭冬.牛头刨床六杆机构的优化设计及仿真[J].机械传动,2013,37(3):52-55.

LÜ K,YUAN Y,GUO D.Optimization design and simulation of six-bar mechanism of shaper[J].Journal of Mechanical Transmission,2013,37(3):52-55.

[2] 张卫亮,魏琳.基于ADAMS牛头刨床六杆机构的运动学计算和仿真[J].宝鸡文理学院学报,2014,34(4):56-59.

ZHANG W L,WEI L.Kinematic calculation and simulation of the six bar linkage of the shape based on the ADAMS[J].Journal of Baoji University of Arts and Sciences,2014,34(4):56-59.

[3] 刘文龙,苏丹,刘明涛.基于Matlab与C语言联合对牛头刨床机构的优化研究[J].河南工程学院学报,2015,27(3):45-51.

LIU W L,SU D,LIU M T.Optimization research of shaping machine based on Matlab and C[J].Journal of Henan University of Engineering,2015,27(3):45-51.

[4] 王延龙.基于PRO/E和ADAMS的牛头刨床六杆机构的运动仿真和优化设计[D].延边:延边大学,2016.

WANG Y L.Motion simulation and optimization design of shaper six bar linkage based on PRO/E and ADAMS[D].Yanbian:Yanbian University,2016.

[5] 张义民,黄贤振,贺向东.不完全概率信息牛头刨床机构运动精度可靠性稳健设计[J].机械工程学报,2009,45(4):106-109.

ZHANG Y M,HUANG X Z,HE X D.Reliability-based robust design for kinematic accuracy of the mechanism under incomplete probability information shaper[J].Journal of Mechanical Engineering,2009,45(4):106-109.

[6] 黎新,王国彪.牛头刨床的遗传优化设计[J].机床与液压,2006(10):40-43.

LI X,WANG G B.Genetic optimum design of quick-return planer[J].Machine Tool & Hydraulics,2006(10):40-43.

[7] 周琦.基于虚拟样机技术的牛头刨床摇杆机构设计研究[D].镇江:江苏大学,2012.

ZHOU Q.Design and research of shaper rocker mechanism based on virtual prototyping[D].Zhenjiang:Jiangsu University,2012.

[8] 敏政,邵翔宇,王乐,等.多目标规划下的牛头刨床优化设计[J].机械与电子,2009(9):24-26.

MIN Z,SHAO X Y,WANG L,et al.Multi-objective planning under the optimum design of shaper[J].Machinery & Electronics,2009(9):24-26.

[9] SOONG R C.An adjustable six-bar mechanism with variable input speed for mechanical forming presses[J].Transactions of the Canadian Society for Mechanical Engineering,2010,32(4):458-466.

[10] SOONG R C.A new design method for single DOF mechanical presses with variable speeds and length-adjustable driving links[J].Mechanism and Machine Theory,2010,45(3):497-507.

[11] 李安.BP神经网络研究与硬件实现[D].青岛:山东科技大学,2010.

LI A.Research and hardware implementation of BP neural network[D].Qingdao:Shandong University of Science and Technology,2010.

[12] 张迅,王平,邢建春,等.基于高斯函数递减惯性权重的粒子群优化算法[J].计算机应用研究,2012,29(10):3710-3713.

ZHANG X,WANG P,XING J C,et al.Particle swamp optimization algorithms with decreasing inertia weight based on Gaussian function[J].Application Research of Computers,2012,29(10):3710-3713.