利用大地边值问题方法统一全球高程基准

赵德军，徐新强，欧阳明达

(1. 信息工程大学地理空间信息学院，河南 郑州 450001； 2. 地理信息工程国家重点实验室，陕西 西安 710054； 3. 西安测绘总站，陕西 西安 710054)

众所周知，当地平均海水面并不重合于全球大地水准面，它们的差异称为海面地形。全球海面地形最大差异可达2 m。例如，我国东海地区各长期验潮站的平均海面比青岛验潮站代表的国家高程基准要高出25 cm左右，而南海验潮站确定的平均海面要高出1985国家高程基准35 cm以上。因此建立在当地平均海水面上的各国高程基准就不一样。目前全世界存在超过100个高程基准，如何统一它们成为大地测量、海洋学界努力的目标。

通常有3种方法统一高程基准：①精密水准测量法。最著名的工程就是欧洲垂直参考框架EVRF2007，将27个国家不同高程系统、不同潮汐系统的高程基准统一为正常高系统、零潮汐系统[1]；以及北美大陆垂直基准NAVD88，通过美国、加拿大和墨西哥水准网重新平差而来。②海面地形法。随着卫星测高技术的发展，已能以3～5 cm的精度确定平均海水面，因此可尝试通过海面地形的方法来统一高程基准。文献[2]通过对北美太平洋、大西洋沿岸、欧洲大西洋沿岸的130多个具有GNSS大地高的验潮站资料分析发现，平均海面高模型结合GOCE+EGM2008重力大地水准面能以分米级的精度传递高程基准。③重力位差法。该方法是确定局部高程零点的重力位，又分为两类：一种是正高或正常高反算法，即根据正高或正常高的定义反算高程基准零点的重力位，文献[3—6]利用该方法计算了我国1985国家高程基准零点的重力位，文献[7]用该方法实现了沿海岛礁高程传递，文献[8]用该方法确定了希腊16个岛屿水准原点重力位，但这种方法需要用全球重力位系数模型来计算水准点的重力位，位系数模型的精度是影响该方法的一个重要因素；另一种方法就是基于大地边值问题方法，该方法利用含有局部高程基准信息的“有偏”重力异常，按边值问题理论确定重力大地水准面，从而间接解算出局部高程基准位差。

基于边值问题法最早由Colombo提出，后经Rummel等进一步拓展，发展为利用改化的Stokes积分公式计算不同基准之间的位差[9-10]。文献[11]应用该方法计算出的瑞典高程与芬兰高程系统的系统差异与水准测量结果一致。文献[12—13]将该方法引入中国，并拓展了正常高系统中高程零点重力位的计算方法[12]。但是依赖于局部高程基准信息的“有偏”重力异常会干扰重力位差的解算，引出“间接偏差项”的概念，这也是该方法没有流行起来的原因。有两种方法处理间接偏差项，一种是新西兰采用的迭代法，首先用“有偏”重力异常确定出一个粗略的高程基准位差，然后用这个粗略的高程基准位差去改正“有偏”重力异常，再次计算较精确的高程基准位差，如此反复迭代[14]。我国海岛(礁)测绘工程中也采用新西兰的迭代法来确定大陆高程基准重力位。另一种方法是利用GOCE卫星重力场模型计算中长波的全球大地水准面，以此来减弱间接偏差项的影响。2010年欧空局推出了“GOCE+”项目，其第1个主题就是探索GOCE卫星重力场统一全球高程基准的能力，由于纯卫星重力大地水准面不受任何局部高程基准影响，可以作为全球高程基准。特别是文献[15—16]从理论上证明了利用200阶次的GOCE卫星重力场，间接偏差项将小于1 cm，从而可忽略其影响。

文献[9—16]中确定局部高程基准重力位差的方法，无论是Stokes解，还是Molodensky解，均是基于第三边值问题。后来我国学者提出采用线性固定重力边值问题法来确定高程基准位差，并成功应用于深圳和香港的高程基准统一[17]。其基本原理为：与重力异常相比，GNSS大地高和重力确定的扰动引力独立于任何高程基准，是“无偏”扰动引力，其线性化球近似的解其实就是第二边值问题解，可得到独立于任何高程基准的重力水准面，用此独立的重力水准面作为标尺来统一全球高程基准。由于GNSS技术出现之前的重力数据均以重力异常表示，使得目前基于第二边值问题的方法还难以推广。因此，本文还是以基于第三边值问题来讨论如何联接各局部高程基准。

1 大地边值问题法

如上文所述，无论基于第二、还是第三大地边值问题，统一高程基准的关键是要确定独立于任何高程基准的全球统一的大地水准面或似大地水准面。

1.1 (似)大地水准面之间的平行性

大地水准面是重力等位面，其上的重力位处处相等。任何一个局部高程基准l与全球高程基准W0之间的位差Cl0也处处相等，它们之间的差距为

(1)

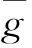
大地水准面具有平行性，但似大地水准面不是重力等位面，似大地水准面之间是否平行文献[16,18]给出了证明：似大地水准面虽不是重力等位面，但重力位差Cl0却处处相等，因此似大地水准面之间的差距为

(2)

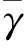
1.2 纯地面重力的边值问题解

本文以Stokes理论为例来解第三边值问题，Molodensky理论参见文献[12,18]。根据广义布隆斯公式，局部高程基准的大地水准面Nl与全球大地水准面上扰动位T0的关系为[9-11]

(3)

式中，ΔW0=W0-U0，为大地水准面重力位W0与参考椭球正常重力位U0之差；γ为参考椭球面上的正常重力。在Stokes理论中，要确定全球大地水准面需要全球大地水准面上的重力异常，但是只能得到局部高程基准l中的重力异常，全球大地水准面上和局部大地水准面重力异常关系为[9-11]

(4)

式中，Δg为从地面归算到全球大地水准面上的重力异常；Δgl为从地面归算到局部大地水准面l上的重力异常，因其严重依赖于局部高程基准，也称“有偏”重力异常；R为地球平均半径。式(4)表明，全球大地水准面上的重力异常Δg，可用局部高程基准上的重力异常Δgl来表示。第三边值问题的广义Stokes解为

(5)

式中，δGM=GM-GM0，为实际地球质量引力常数GM和参考椭球质量引力常数GM0之差；S(ψ)为Stokes函数。进一步整理得到

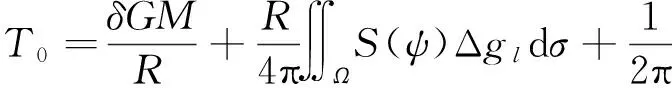
(6)

若存在K个高程基准，每个高程基准中重力位差Ck0只有一个，则式(6)右端第3项可以用和的形式表示，即

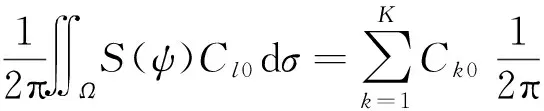
(7)

将式(6)和式(7)代入式(3)，得

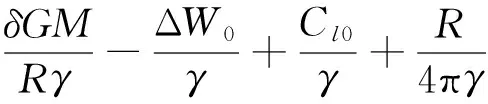
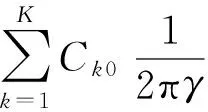
(8)

令

(9)

式中，Nzero为大地水准面0阶项，目前能精确确定，可作为已知量。令

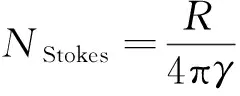
(10)

式中，NStokes为地面重力异常计算的大地水准面，可作为已知量。令

(11)

式中，Nind称为间接偏差项，其中

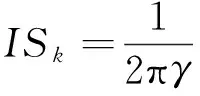
(12)

则式(8)形式上可简化为

(13)

式中，Nl=h-Hl，h为GNSS获取的大地高，Hl为局部高程基准中的正高，Nl为已知量。

式(14)中未知量存在直接位差Cl0，以及其他高程基准中的位差Ck0。可按式(13)建立观测方程，平差解算出未知量，文献[9]建立了平差模型，文献[19]根据已有观测资料将全世界分成亚洲、欧洲、非洲等7个高程基准进行模拟计算。由于Stokes函数收敛速度慢，因此其积分需要跨越多个高程基准，使得观测方程变得复杂，而不实用。

1.3 联合卫星和地面重力的边值问题解

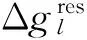
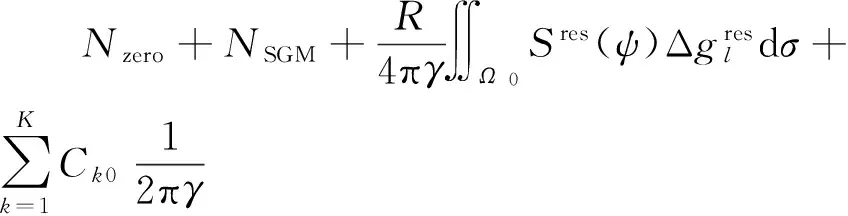
(14)

(15)

式中，Pn(cosψ)为勒让德级数。改化Stokes核函数的作用为加速积分收敛，减小球冠Ω0积分面积，同时间接偏差项变为

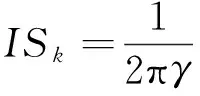
(16)

对比式(16)和式(12)，区别仅仅在于改化Stokes核函数，但是却起到了惊人的效果。文献[15]证明使用50阶次的卫星重力，即改化Stokes核函数nmax=50时，间接偏差项ISk影响小于3 cm；而使用200阶次的卫星重力(nmax=200)，间接偏差项ISk影响小于1 cm，因而可直接忽略间接偏差项的影响。联合卫星重力场和地面重力的全球大地水准面为

(17)

最后给出高程基准重力位差的计算式为

Cl0=γ(h-Hl-N0)

(18)

正常高系统中，重力位差的计算式为

(19)

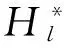
2 数值试验

2.1 GNSS/水准数据

GNSS/水准数据采用美国大地测量局NGS的GNSS/水准数据集——GPSBM2009，该数据集参与了美国混合大地水准面GEOID12A的构建。GPSBM2009数据的大地基准采用北美大地基准NAD83，高程基准采用北美高程基准NAVD88。NAD83坐标系原点与现代ITRF地心存在约2 m的偏差，定向也存在一定的系统差，因此数据预处理时采用NGS提供的Htdp坐标转换软件，将大地坐标转换到ITRF2008框架[22]。NAVD88属于单验潮站确定的高程基准，通过重新平差美国、加拿大、墨西哥历史上几十年的水准测量数据获得，并非开展北美全洲统一的水准测量，存在一定的系统差，尤其在美加边境。因此加拿大最终放弃了NAVD88高程基准，仍采用CGVD28作为法定高程基准，只有美国、墨西哥采用NAVD88作为法定高程基准。

2.2 重力大地水准面

从加拿大自然资源部收集了加拿大重力水准面CGG2010，其采用200阶次的GOCE重力场模型goco01s，覆盖范围包括加拿大和美国[23]。美国大地测量局收集了美国重力水准面USGG2012，其采用200阶的GOCE模型goco02s，覆盖范围包括美国和加拿大大部分国土。250阶次的GOCE和251～2160阶次的EGM2008组合的重力大地水准面GOCE+EGM08，GOCE有多种版本，经比较第5代直接法解算的模型精度较高[22]。

2.3 重力位差

NAVD88高程基准在美国境内与GOCE重力水准面存在明显的东西方向和南北方向的倾斜(如图1 所示)，因此采用2参数曲面模型来吸收系统误差，即

δN=x1(φp-φ0)+x2(λp-λ0)cosφp

(20)

式中，δN=hNAD83-HNAVD88-NGG为大地水准面差异，hNAD83为GNSS大地高，HNAVD88为赫尔默特正高，NGG为重力大地水准面；φp、λp分别为GNSS/水准点的大地纬度、经度；φ0、λ0分别为水准网几何中心的大地纬度、经度；x1、x2分别为南北、东西方向水准面的倾斜度，是未知量。结合式(18)和式(20)计算了美国高程基准位差。表1中第2列为NAVD88高程基准与W0的重力位差，第3列为高程基准垂直差距，第4、5列分别为南北、东西方向的倾斜度。可以看出，CGG2010、GOCE+EGM08重力水准面之间较吻合，但USGG2012与其他二者相差了约3 cm。因此取三者均值，最终确定美国高程基准与全球高程基准重力位差为-4.82±0.05 m2s-2，垂直偏差为-49.2±0.5 cm。

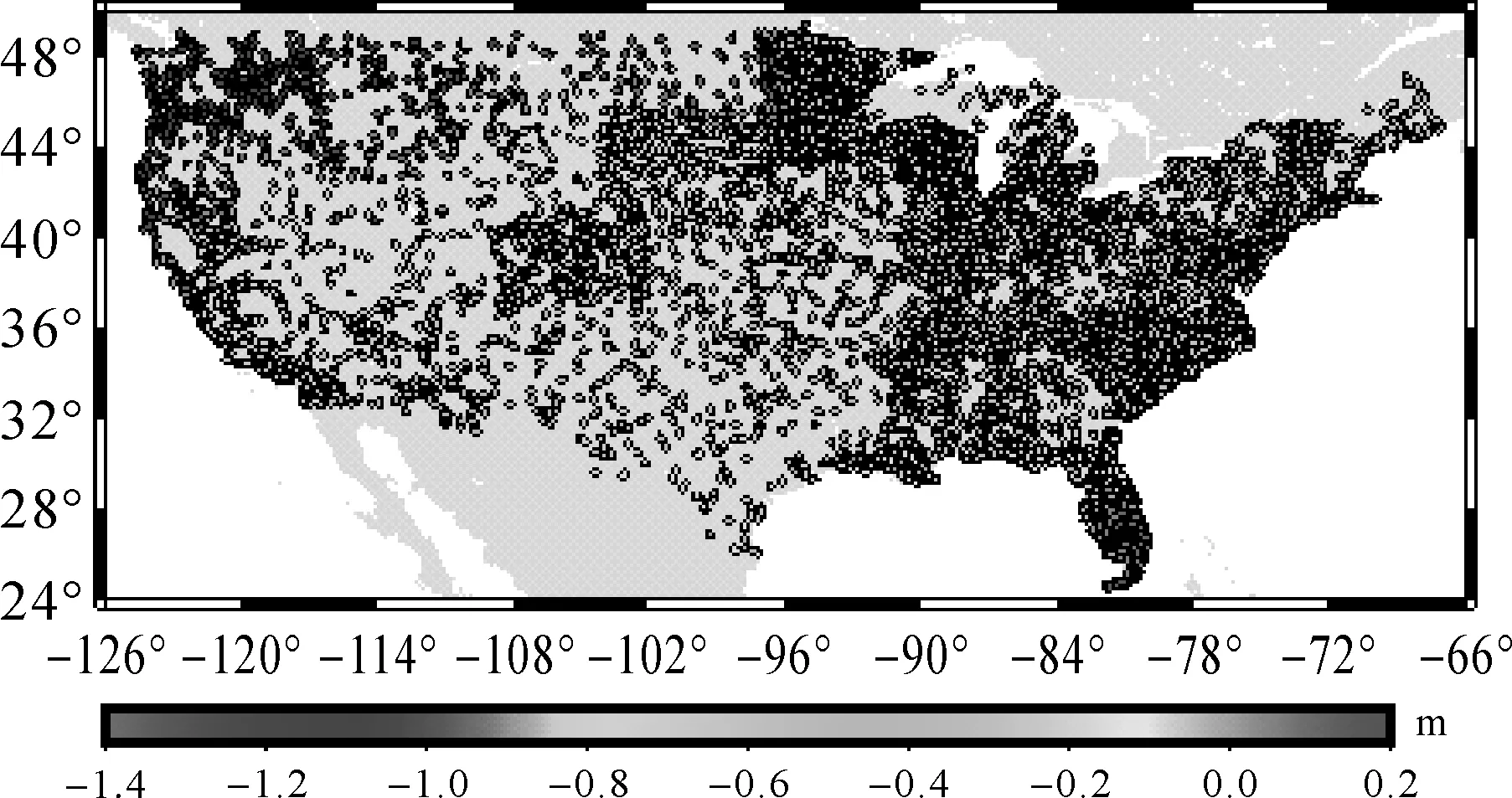
图1 NAVD88高程基准面系统偏差

重力水准面Ci0/m2s-2δN/cmx1/(m/°)x2/(m/°)CGG2010-4.71±0.05-48.08±0.5-0.0360.013USGG2012-5.01±0.05-51.13±0.5-0.0360.013GOCE+EGM08-4.73±0.05-48.29±0.5-0.0350.013

3 结论与建议

本文利用含有局部高程基准的“有偏”重力异常、局部高程基准的正高，按第三边值问题推算了局部高程基准重力位差的计算方法。针对间接偏差项，利用卫星重力场模型和改化积分核减弱其影响。得出如下结论与建议：

(1) 大地边值问题法确定高程异常差会引入间接偏差项。充分利用200阶的GOCE卫星重力场，间接偏差项小于1 cm，可以忽略不计。

(2) 利用实测GNSS/水准数据确定美国高程基准NAVD88与全球高程基准差为-49.2±0.5 cm。

(3) EGM08重力场模型构建时，采用60阶GRACE卫星重力场模型GGM02S作为其低阶项，对无重力数据区域或数据专利区域，采用剩余地形模型来填充。因此EGM08在许多地方精度较低，而且60阶的GRACE卫星重力场模型并不能完全消除间接偏差项的影响。因此建议，对于有地面重力数据的地区，应联合GOCE和地面重力按边值问题解算高精度的重力大地水准面，从而确定高程基准差；对于无地面重力数据的地区，可用GOCE+EGM08组合的重力大地水准面来确定高程基准差。

参考文献：

[1] SACHER M，IHDE J，LIEBSCH G．EVRF2007 as Realization of the European Vertical Reference System[J]．Bollettino Di Geodesia E Scienze Affin，2009，68：35-50．

[2] WOODWORTH P，HUGHES C W，BINGHAM R J．Towards Worldwide Height System Unification Using Ocean Information[J]．Journal of Geodetic Science，2012，2(4)：302-318.DOI:10.2478/v10156-012-0004-8.

[3] 焦文海，魏子卿，马欣，等．1985国家高程基准相对于大地水准面的垂直偏差[J]．测绘学报，2002，31(3):196-200．

[4] 郭海荣，焦文海，杨元喜．1985国家高程基准的系统差[J]．武汉大学学报(信息科学版)，2004，29(8)：715-717.

[5] 翟振和，魏子卿，吴富梅．利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J]．大地测量与地球动力学，2011，31(4):116-118.

[6] 赫林，李建成．褚永海．1985国家高程基准与全球高程基准之间的垂直偏差[J]．测绘学报，2016，45(7):768-774．DOI:10.11947/j.AGCS.2016.20160029．

[7] 吴富梅，魏子卿．利用GNSS和EGM2008模型进行跨海高程传递[J]．武汉大学学报(信息科学版)，2016，41(5)：698-703.DOI:10.13203/j.whugis20140392.

[8] KOTSAKIS C．Estimation of the Zero-height Geopotential Level WLVD0 in a Local Vertical Datum From Inversion of Co-located GPS，Leveling and Geoid Heights:A Case Study in the Hellenic Islands[J]．Journal of Geodesy，2012，86(6):423-439．DOI：10.1007/s00190-011-0530-7.

[9] RUMMEL R，TEUNISSEN P．Height Datum Definition，Height Datum Connection and the Role of the Geodetic Boundary Value Problem[J]．Bulletin Géodésique，1988，62(4):477-498.

[10] SANSO F，USAI S．Height Datum and Local Geodetic Datums in the Theory of Geodetic Boundary Value Problems[J]．Allgemeine Vermessung Nachrichten，1995，102:343-355.

[11] PAN M，SJOBERG L E．Unification of Vertical Datums by GPS and Gravimetric Geoid Models With Application to Fennoscandia[J]．Journal of Geodesy，1998，72(2):64-70.

[12] 莫登沅．高程基准统一问题的研究[D]．郑州：信息工程大学，2000.

[13] 徐菊生，王建华，赖锡安，等．垂直基准定义及联接[J].地壳形变与地震，2001，21(1)：24-34.

[14] AMOS M J，FEATHERSTONE W E．Unification of New Zealand’s Local Vertical Datums: Iterative Gravimetric Quasigeoid Computations[J]．Journal of Geodesy，2009，83(1)：57-68.

[15] GERLACH C，RUMMEL R．Global Height System Unification with GOCE:A Simulation Study on the Indirect Bias Term in the GBVP Approach[J]．Journal of Geodesy，2013，87(1):57-67．DOI:10.1007/s00190-012-0579-y．

[16] GATTI A，REGUZZONI M，VENUTI G．The Height Datum Problem and the Role of Satellite Gravity Models[J]．Journal of Geodesy，2013，87(1):15-22．DOI：10.1007/s00190-012-0574-3.

[17] ZHANG L，LI F，CHEN W，et al．Height Datum Unification Between Shenzhen and Hong Kong Using the Solution of the Linearized Fixed-gravimetric Boundary Value Problem[J]．Journal of Geodesy，2008，83(5)：411-417．DOI:10.1007/s00190-008-0234-9．

[18] JEKELI C．Heights，the Geopotential，and Vertical Datums[C]∥Report 459.[S.l.]：The Ohio State University，2000．

[19] XU P．A Quality Investigation of Global Vertical Datum Connection[J]．Geophysical Journal International，1992，110(2)：361-370．DOI:10.1111/j.1365-246X.1992.tb00880.x．

[20] 傅露，褚永海．区域大地水准面确定中Stokes核函数的应用[J]．大地测量与地球动力学，2013，33(2):110-113．

[21] 赫林，李建成．褚永海．1985国家高程基准与全球高程基准之间的垂直偏差[J]．测绘学报，2016，45(7)：768-774．DOI:10.11947/j.AGCS.2016.20160029．

[22] 赵德军．GOCE重力场模型的精度评估[J]．大地测量与地球动力学，2015，35(2)：21-25．

[23] HUANG J，VERONNEAU M．Canadian Gravimetric Geoid Model 2010[J]．Journal of Geodesy，2013，87(8)：771-790．