改进MSAC估计F与H矩阵在匹配点中的提纯

李 城，王仁礼，王成港，明平寿

(山东科技大学山东省基础地理信息与数字化技术重点实验室，山东 青岛 266590)

寻找两幅影像相同场景或物体的同名点在摄影测量与计算机视觉领域有着诸多应用，如相机标定[1]、三维重建、影像校正[2-3]、影像拼接[4]和特征追踪等。然而影像匹配难免会存在误匹配，错误的对应关系会直接影响后续的工作。对多视影像来讲，通常采用两种约束：一是极线约束，即点与线的对应关系；二是单应约束，即点与点的对应关系。因此，常常估计基本矩阵或单应矩阵来剔除误匹配点。到目前为止，基本矩阵/单应矩阵的估计方法可分为线性估计方法、迭代估计方法和稳健估计方法。其中线性估计方法代表有8点算法；迭代估计算法中最具代表性的为非线性最小二乘法；稳健性算法是最具有抗噪性的算法，其主要分为非随机抽样算法如M估计算法[5]、LMedS[6]、LTS[7]和随机抽样算法如RANSAC[5,8]、MSAC[9]、MLESAC[9]等一系列通过修改RANSAC代价函数的衍生算法。但是非随机抽样算法只能容忍不超过50%的“溃点”[7]，限制了它们的适用性[10]。故稳健随机抽样算法在目前广泛应用，然而又因为随机抽样算法没有考虑到抽取特征点的位置，这就有可能造成抽取的样本成线性分布或彼此之间太过紧凑，从而导致估计的F/H矩阵准确性下降，因此本文通过改进其抽样模式来尽可能地避免这一劣势。同时，本文在基于改进MSAC算法估计F/H矩阵的基础上，采用不同地物类型的影像，通过大量试验比较了两种提纯方式的适用场景。

1 算法原理

1.1 基本矩阵

在计算机视觉中，立体像对的同名点之间必关联一个3×3的基本矩阵；在对极几何中，基本矩阵是同名点的齐次坐标x与x′的对应关系，Fx描述的是另一幅影像上的同名点x′所在的极线[7]，这就意味着所有的同名点必满足

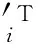
(1)

这种约束有利于搜索和检测错误的对应关系。换言之，基本矩阵描述的同名点之间的关系也可被称为极线约束。

1.2 单应矩阵

平面单应性是基本矩阵的一种特殊形式，即当所有的物点都位于同一平面上时，两幅影像同名点之间存在一一对应的关系，这种关系可以用单应矩阵来描述，其实质是一种严格的透视变换关系[8,11-13]。

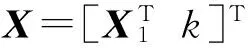
X2=P′X=[A|a]X=AX1-avTX1=(A-avT)=HX1

(2)

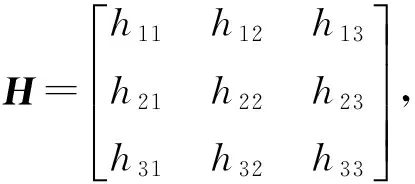
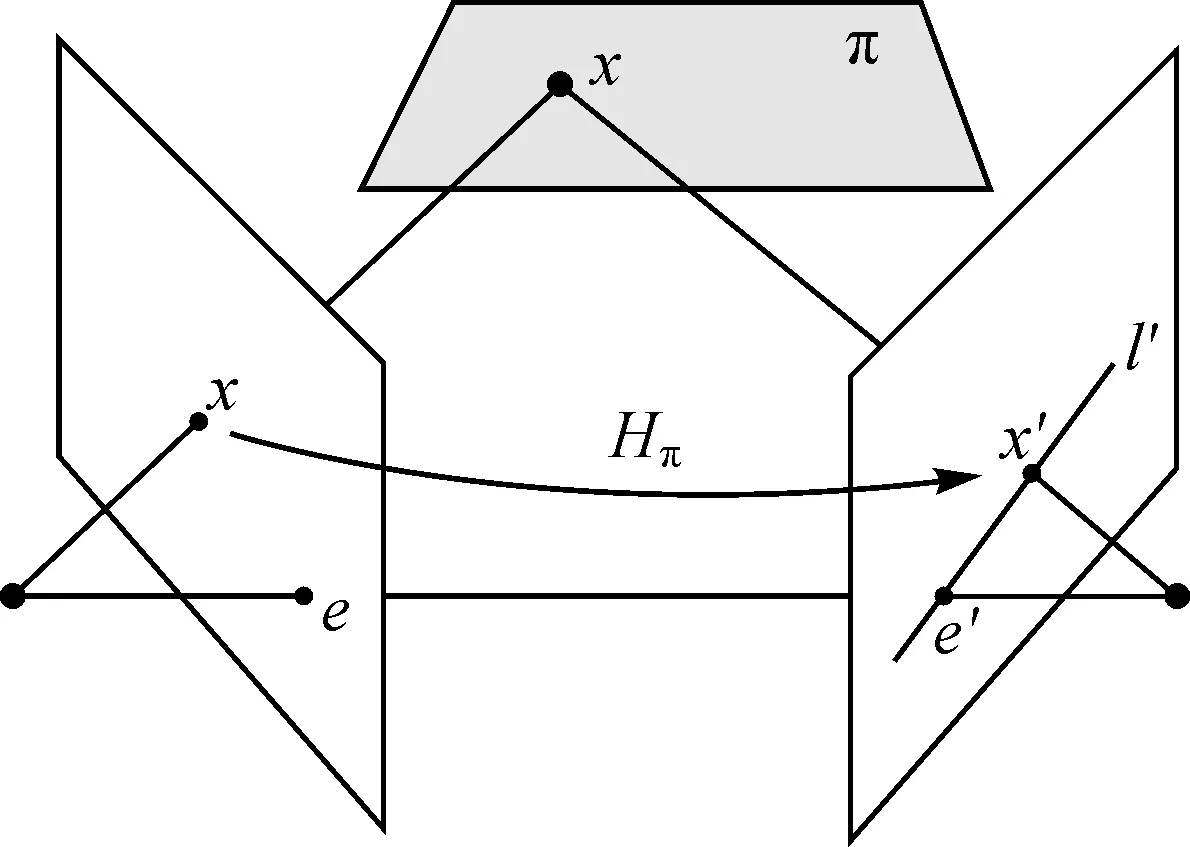
图1 平面单应

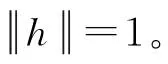
将式(2)展开即得：

(3)

1.3 基本矩阵与单应矩阵的联系与区别

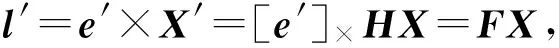
1.4 改进MSAC估计F和H矩阵

MSAC算法是RANSAC的变体，通过对RANSAC代价函数的修改，克服了RANSAC对阈值敏感的缺点。同时，MSAC算法不仅反映了模型数据的数目，而且反映了模型数据的拟合程度，因此在整体上要优于RANSAC算法。但是，同RANSAC算法一样，它们均是随机抽样算法，每次抽取样本的分布情况对估计的基本矩阵/单应矩阵的性能有影响[15]。因此，本文在抽样时，以所有匹配点集的质心为基准点建立坐标系，使样本点分布在4个象限，且样本点两两之间的距离大于某个阈值，以便尽可能地均匀分布于整个重叠区域，避免了估计的基本矩阵/单应矩阵是局部最优而非整体最优。

改进后的MSAC算法估计F和H矩阵步骤如下：

(1) 初始化3*3的F/H为零矩阵。

(2) 设置计数器n=0和循环次数N。

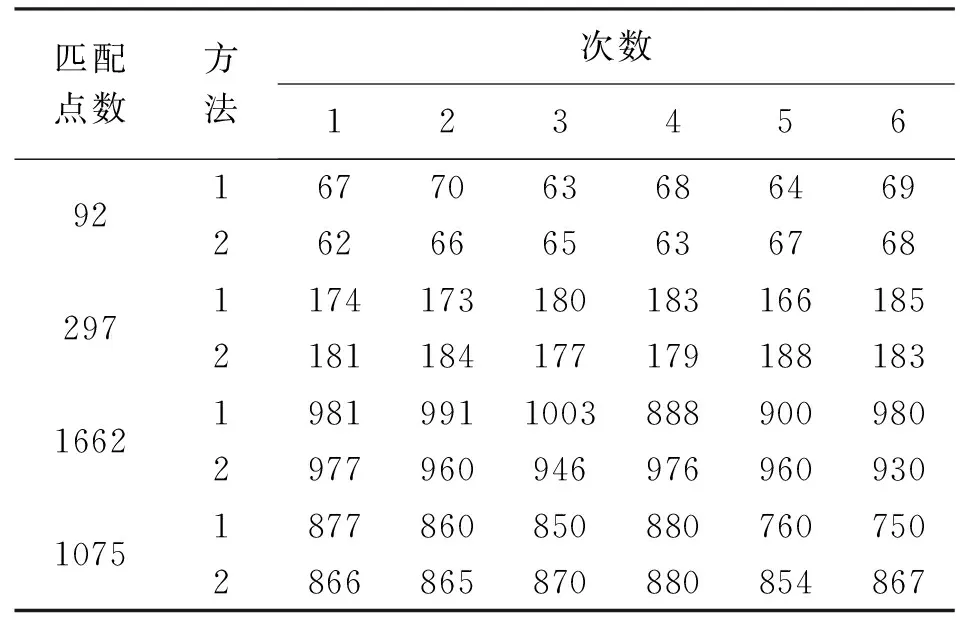
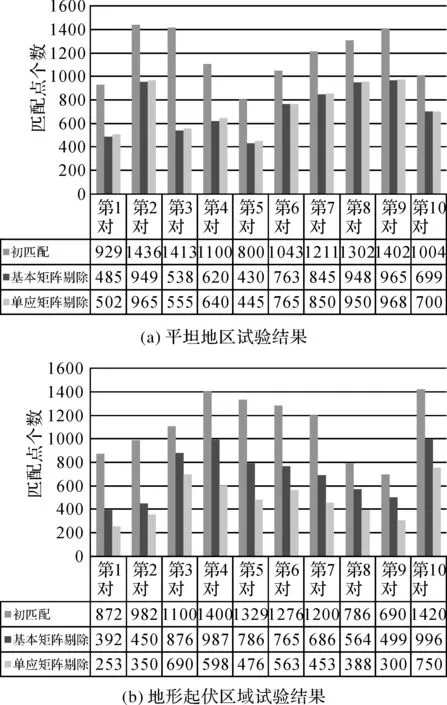
(3) 设置条件当n

a. 以像对匹配点集的质心为原点建立坐标系。

b. 使用随机器产生8对同名点对或4对同名点对。

c. 若样本点没有分布在4个象限且两两之间的距离小于某个阈值，重复步骤b；反之，进行下一步。

d. 计算基本矩阵/单应矩阵(f/h)。

e. 计算除样本点外所有剩余同名点的拟合程度。

f. 如果f/h的拟合优于F/H，用f/h替换F/H，更新循环次数N。

g. 计数器累加，直至达到最后的抽样次数N。

(4) 若提前达到符合数目的模型(如85%的内点)，则提前跳出循环。

(5) 记录含有最多内点的模型，该模型为最优的F/H。

2 试验结果与分析

2.1 改进MSAC算法抽样模式的试验效果

本文改进了抽样模式，使得每次抽样尽可能均匀分布，且避免了抽取的样本太过聚集而导致估计的基本矩阵/单应矩阵不能反映整体状况。本文每对像对进行6次试验，比较改进前与改进后的MSAC算法剔除误匹配点后的最终匹配点数目，见表1。

表1 改进前(方法1)与改进后(方法2)的对比

由表1可以看出，当匹配点数目不多时，改进后效果不是太明显。而当匹配点数目较多时，改进前每次提纯之后的结果最大差异达到了约100个匹配点，但此时改进后每次提纯之后的结果最大差异不超过50个匹配点。因此，在不影响匹配点数目的情况下，改进MSAC算法的抽样模式使得每次提纯之后的结果相对稳定。

2.2 F和H矩阵提纯效果

分别选取10对平坦地区的航片像对和具有明显地形起伏的航片像对进行试验，影像大小皆为6000×4000。图2是平坦地区和地形起伏地区的部分航片图，图3是平坦地区和地形起伏地区的试验结果。

图2 部分试验影像

图3

因为改进后的MSAC算法依然是不确定模型，所以每一对影像的最终匹配点数目取100次结果的平均值。图3(a)试验影像的第1对、第2对和第3对是田地、第4对、第5对和第6对是草地，剩下的是小的灌木林地，根据试验结果可以看出，对于影像中的场景是平面或者近似平面的话，经过估计基本矩阵和单应矩阵剔除完误匹配后，两者最终的匹配点数目相差不大。但是有一点值得注意，当抽样所选的同名点都满足共面的话，所估计的基本矩阵就会退化，即所计算的基本矩阵不准确，这便会导致在剔除误点时，有些错误的点也会被认为满足极限约束。如图4所示，以平坦地区的田地为例，1—12号点对是正确的匹配点，13—18号点对是人为添加的错误匹配点。经过单应矩阵和基本矩阵提纯之后，如图5所示，在基本矩阵提纯的情况下，14、17、18号点仍然被认为是内点，而在单应矩阵提纯的情况下，在平面影像上，其利用匹配点二维约束的强限制条件，人工添加的误点全部被剔除。

图4 匹配点分布

图5 提纯结果对比

图3(b)试验的前3对影像主要是以参差不齐的房屋为主，剩下的是山区影像，地形起伏很大。可以看出前3对影像中的房屋导致影像存在深度变化的场景，基于单应矩阵剔除完误匹配点后的结果开始少于基本矩阵，在随后山区中的影像，这种视差变化更加明显，基于单应矩阵剔除了不少正确的点对，这种方法开始失效。因此当两幅影像的场景起伏非常明显时，影像之间对应像素之间的位置关系就不能用一个单应矩阵H来描述，或者说此时一张影像的匹配点经过单应变换后在另一张影像上只能确定其近似(可能)位置，即可以运用单应矩阵预测点位。

3 结 语

对于误匹配点的剔除，本文采用了改进MSAC稳健性算法估计基本矩阵和单应矩阵进行提纯。通过大量的试验，验证了改进MSAC算法的可行性，比较了两种提纯方式的适用场景，结果表明：

(1) 改进后的MSAC算法尽可能地弥补了随机抽样的不均匀性，性能较原算法有所改善。

(2) 对于影像场景中几乎没有深度信息或变化微小的情况下，如平坦的地面或墙壁等，要利用单应矩阵将匹配点一一对应的特点来剔除误匹配点；而当影像场景中有着明显的视差时，如地形起伏大的山区、走廊或者街道等，要估计基本矩阵来对误匹配点进行剔除。

参考文献：

[1] DUAN Y N，CHEN W，WANG M Z，et al.A Relative Radiometric Correction Method for Airborne Image Using Outdoor Calibration and Image Statistics[J].IEEE Transactions on Geoscience and Remote Sensing,2014，52(8)：5164-5174.

[2] LINGER M E，GOSHTASBY A A.Aerial Image Registration for Tracking[J].IEEE Transactions on Geoscience and Remote Sensing,2015,53(4)：2137-2145.

[3] YE P，LIU F，ZHAO Z.Multiple Gaussian Mixture Models for Image Registration[J]，IEICE Transactions on Information and Systems，2014，97 (7)：1927-1929.

[4] ZARAGOZA J，CHIN T J，TRAN Q H，et al.As-projective-as-possible Image Stitching with Moving DLT[J].IEEE Conference on Computer Vision and Patlern Recognition，2013，36(7):2339-2346.

[5] TORR P H，MURRAY D W.The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix[J].International Journal of Computer Vision,1997,24(3):271-300.

[6] ZHANG Z.Determining the Epipolar Geometry and Its Uncertainty：A Review[J].International Journal of Computer Vision,1996,27(2):161-195.

[7] ROUSSEEUW P J，LEROY A M.Robust Regression and Outlier Detection[J].Wiley-Interscience,2003,31(2):260-261.

[8] HARTLEY R，ZISSERMAN A.Multiple View Geometry in Computer Vision[M].[S.l.]：Cambridge University Press，2003:159-239.

[9] TORR P H S，ZISSERMAN A.MLESAC：A New Robust Estimator with Application to Estimating Image Geometry[J].Computer Vision and Image Understanding,2000，78(1)：138-156.

[10] WANG H，SUTER D.MDPE：A Very Robust Estimator for Model Fitting and Range Image Segmentation[J].International Journal of Computer Vision，2004，59(2):139-166.

[11] CHUM O，WERNER T，MATAS J.Two-View Geometry Estimation Unaffected by a Dominant Plane[J].IEEE Computer Society Conference on Computer Vision and Patlern Recognition，2005,1(1):772-779.

[12] FRAHM J M，POLLEFEYS M.RANSAC for(Quasi-)Degenerate Data (QDEGSAC)[J].IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2006,1(1)：453-460.

[13] RAGURAM R，CHUM O，POLLEFEYS M，et al.USAC：A Universal Framework for Random Sample Consensus[J].IEEE Transactions on Pattern Analysis & Machine Intelligence，2013，35(8):2022-2038.

[14] LUONG Q T，FAUGERAS O D.The Fundamental Matrix：Theory，Algorithms，and Stability Analysis[J].International Journal of Computer Vision,1996，17(1):43-75.

[15] JO G S,LEE K S，CHANDRA D，et al.RANSAC versus CS-RANSAC[C]∥Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence.[S.l.]：AAAI,2015.