利用主成分分析法及地理加权回归模型分析AOD数据

李广超，李如仁，卢月明，赵阳阳，余 博

(1. 沈阳建筑大学交通学院，辽宁 沈阳 110168； 2. 中国测绘科学研究院，北京 100830)

全球大气气溶胶类型和含量变化与气候变化和大气环境污染密切相关，是气象学、环境学和医学研究关注的热点问题[1]。气溶胶光学厚度作为大气气溶胶最重要的参数之一，是表征大气混浊度或大气中气溶胶总含量的重要物理量[2]。许多学者对气溶胶光学厚度影响因素的相关性进行了研究，发现地理数据(高程等)和气象数据(湿度等)是影响AOD数据的显著因素[3-6]。因此，可采用气象数据和地理数据来估算AOD数据。在地学空间分析中，观测数据是在不同的空间位置上获取的，全局空间回归模型就是假定回归参数与样本数据的地理位置无关，而在实际问题研究中经常发现回归参数随地理位置变化，这时如果仍采用全局空间回归模型，得到的回归参数估计将是回归参数在整个研究区域内的平均值，不能反映回归参数的真实空间特征[7-8]。当空间数据存在自相关时，地理加权回归(geographically weighted regression，GWR)模型提供了一个优于传统OLS模型的估计方法，传统的OLS方法仅仅提供全局参数的估计，GWR容许分解成局部参数估计，深刻地阐释了地理空间数据的某类指标和空间影响因子之间的关系，是传统OLS无法比拟的[9]。GWR模型是一种典型的局部模型，认为回归系数随着空间位置的变化而变化，具有空间非平稳性[10]。

近年来，许多研究者对GWR进行了研究。在GWR模型应用方面，武文娟等[11]以四川省县公立医院床位数为例，利用空间分析技术研究了区县床位的时空变化特征，并采用GWR解释了经济、人口、交通、地形等因素对其时空变异性的影响。董冲亚等[12]应用地理加权回归模型探讨了气象因素和大气污染因素影响我国女性肺癌发病的空间属性，结果表明东北地区尤其是辽东半岛为我国女性肺癌的高发区域，具有明显的地区集聚性。孙伟伟[13]以长三角经济区为例，采用MODIS/Terra AOT时序卫星影像产品为数据源，构建AOD-PM2.5季节地理加权回归模型，为PM2.5区域联防联控提供了信息支撑和科学依据。陈辉等[14]采用GWR进行回归分析，构建了我国区域范围内近地面的PM2.5遥感反演模型，结果表明利用GWR进行PM2.5遥感估算，既能体现PM2.5时空分布的全局变化特征，又能从局部体现全国PM2.5组分、污染程度及垂直分布结构的空间差异性特性。庞瑞秋等[15]以吉林省各县域为基本单元，结合GWR和空间相关分析方法，讨论了人口城镇化水平与国有动力、农业动力及外向动力等因素的空间相关关系，并依次解释人口城镇化分县域差异的影响因素。在GWR模型改进方面，赵阳阳等[16]将半监督学理论与GWR相结合，提出基于半监督学习的地理加权回归方法，并通过试验验证了该方法在模型性能上的优势。覃文忠等[17]以迭代算法为基础，推导出混合GWR的常系数(全局参数)和变系数(局部参数)的计算方法，并以上海市楼盘价格进行验证，结果表明混合GWR的计算量略大于GWR，但对样本数据的拟合效果更好，局部参数估计更稳健。赵阳阳等[18]基于贪心算法，通过引入Akaike信息法则，设计了适用于GWR的特征变量选择方法。

由上述研究可以得出，AOD数据也可以利用GWR模型进行建模，但如果只是简单地加入到模型计算中，没有考虑各个影响因素之间的共线性，且考虑的影响因素较多会严重影响模型的计算效率。针对上述问题，刘蓓[19]将非线性主成分分析法(nonlinear principal component analysis，NLPCA)应用于岩体质量等级分类问题中，构建了岩体质量等级分类的非线性主成分综合评价模型，结果表明，该评价模型有效且预测精度高。高青松等[20]提出的非线性检验度量可有效地检测出给定数据集中各变量之间的线性或非线性关系，为是否对数据采用非线性主成分分析提供了依据。檀菲菲等[21]提出了利用非线性主成分分析法和施密特正交化(NLPCA-GSO)相结合的方法评价区域的可持续发展水平来弥补传统方法的不足，结果表明基于NLPCA-GSO的可持续发展水平模型很好地弥补了传统主成分分析及对各子系统结果的综合评价的不足。周永正等[22]提出了非线性主成分分析法与神经网络算法的融合模型，并将非线性主成分神经网络融合模型应用于水泥强度的预测研究，得到的结果表明预测误差很小。孙康等[23]提出了一种基于非线性主成分分析的高光谱图像目标探测算法，试验表明，基于神经网络的非线性主成分分析法可以将线性不可分的目标与背景分离，使用非线性特征和原始特征的组合可以获得更好的目标探测效果。

综上论述，本文提出一种基于主成分分析的地理加权回归方法(PCA-GWR)，该方法检验了AOD影响因素之间的共线性；通过非线性主成分分析法对影响AOD值的若干相关变量进行处理，既消除了相关变量彼此之间的多重共线性，又可以起到降维的作用；再利用得到的较少几个综合指标，通过地理加权回归模型对AOD浓度进行预测；最后通过与常规GWR模型对比，采用MAE、RMSE、AIC、R2作为评价指标，评价了本文方法的有效性。

1 研究方法

1.1 非线性主成分分析

非线性主成分分析是在线性主成分分析基础上的扩展。传统的主成分分析方法在一些情况下降维不好，一般只能处理线性问题。综合评价的实际结果与评价指标间的相关程度高低成正比，评价指标间相关程度越高，主成分分析的结果越好，指标间的相关性越小，每一个主成分承载的信息量就越少，为了满足累积贡献度达到一定水平(通常为85%以上)，可能需要选取较多的主成分，此时主成分分析法的降维效果将会不明显。非线性主成分分析通过对原始数据作中心化对数比变换，将主成分表示为原始数据的非线性组合，可以较好地保留数据本身的非线性特征；分析的出发点是协方差矩阵，而不是之前的相关系数矩阵，这样会明显提升降维效果，用更少的主成分反映更多的原始指标信息，并且评价的稳定性与合理性也有所提高。非线性主成分分析原理如下：

设有P维向量x=(x1,x2,…,xp)的样本资料(xij)n×p

对原始数据作中心化对数比变换

(1)

计算中心化对数比样本协方差矩阵

S=(Sij)p×p

(2)

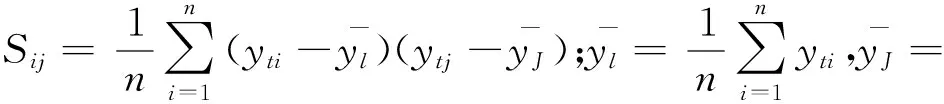
从S出发求样本主成分如下：

设λ1>λ2…>λp是S的P个特征根，(a1,a2,…,ap)是相应的标准化特征向量，则第i个主成分为

(3)

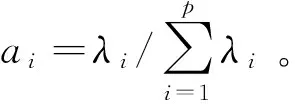
1.2 地理加权回归

地理加权回归是英国圣安德鲁斯大学的Fortheringham等[24]在空间变异系数回归的基础上利用局部光滑思想提出的。地理加权回归是对普通线性回归的扩展，即将样本点的地理位置引入到回归参数中，其公式为

(4)

式中，(yi,xi1,xi2,…,xid)为因变量y和自变量(x1,x2,…,xd)在数据点(ui,vi)处的n组数据值；βk(ui,vi)(k=1,2,…,d)为第i个观测点(ui,vi)处的未知参数；εi(i=1,2,…,n)为独立同分布的误差项，通常假定其服从N(0,δ2)分布。

地理加权回归模型中的回归参数与样本数据的地理位置有关，其影响程度(空间权重)可用一个距离函数表示，该函数简称核函数。常用的核函数有高斯核函数、Bisquare核函数等。GWR模型的关键在于选择核函数，并确定其最优带宽。研究发现，不同核函数的带宽敏感度不同，而带宽的变化对结果影响较大[16]，因此，可通过核函数和带宽来区分回归模型。

核函数的带宽过大会导致回归参数估计偏大，过小则导致回归参数估计偏小[7]。为减小带宽不适造成的误差，本文采用CV交叉验证法[25]来计算最优带宽。CV法计算公式为

(5)

1.3 PCA-GWR原理

本文充分结合了非线性主成分分析法与地理加权回归模型的优势，提出了一种基于主成分分析的地理加权回归方法(PCA-GWR)。该方法在使用GWR预测之前，首先检测数据之间的相关性，然后利用主成分分析法去除数据之间的多重共线性，并得到几个综合指标，在综合指标中选取累积贡献度超过85%的前几个指标作为GWR模型的输入变量，从而对京津冀地区的AOD进行分析预测。PCA-GWR的主要流程为：①利用Pearson相关系数检验主变量相关变量数据之间的相关性；②对存在相关性的数据进行非线性主成分分析预处理，去除数据之间的多重共线性，并得到几个综合指标；③从综合指标中选取累积贡献度超过85%的前几个指标作为GWR模型的输入变量，对主变量(PM2.5浓度)进行分析或预测；④将分析或预测结果与其他模型对比，采用MAE、RMSE、AIC、R2作为评价指标，来验证本文方法的预测精度。

2 试 验

2.1 研究区概况

研究区域选用地理范围为35.5°N—43°N、113°E—120°E的京津冀地区，土地面积约为21.8万km2，包含北京、天津与河北。北京位于华北平原的北部，背靠燕山，有永定河流经老城西南，毗邻天津市和河北省；天津位于华北平原海河五大支流汇流处，东临渤海，北依燕山，海河在城中蜿蜒而过，是天津的母亲河；河北东临渤海、内环京津，辖保定、唐山、石家庄、邢台、邯郸、衡水、沧州、廊坊、秦皇岛、张家口、承德等11个地级市。京津冀是中国北方经济规模最大、最具活力的地区，2015年底人口约为11 143万人，地区生产总值约为69 358.89亿元。随着京津冀经济的快速发展，生态环境也随之破坏严重，因此优化生态环境成为京津冀地区的重要任务。大气气溶胶类型和含量变化与气候变化和大气环境污染密切相关，开展大气气溶胶的研究对大气环境污染分析及防控具有重要意义。

2.2 数据来源

本文以地理空间数据(高程、坡度、坡向)和气象数据(风速、气温、湿度、气压)为自变量，以AOD数据为因变量，估算AOD数据的值。其中地理空间数据来自地理空间数据云网站(http:∥www.gscloud.cn/)，选用SRTMEDM 90 m分辨率原始高程数据、SRTMSLOPE 90 m分辨率坡度数据、SRTMASPECT 90 m分辨率坡向数据；气象数据来自中国气象科学数据共享服务网(http:∥www.escience.gov.cn)，共110个气象监测站点地理位置信息，频率为每天；AOD数据来自 (https:∥ladsweb.nascom.nasa.gov/data)网站的Terra MODIS C06二级气溶胶产品(代号MYD04_3K)，频率为每天，空间分辨率为3 km，本文采用MODIS Collection 6 MYD04_3K数据集中参数名为“Optical_ Depth_ Land_ And_ Ocean”，波段为550 nm的2级AOD数据。本文选择2015年5月期间的气象和AOD数据作为研究对象。京津冀AOD数据采样点分布如图1 所示。(注：1 mile=1.61 km)

2.3 数据预处理

为了数据的时空一致性，对地理空间数据、气象数据、 AOD数据进行预处理， 流程如图2所示。首先对气象数据进行处理，采用SQL Server求110个气象站点处日均值，再利用Java语言程序求气象数据的月均值；其次对地理空间数据进行处理，将高程、坡度、坡向影像数据进行投影坐标转换，再利用ArcGIS10.2对高程、坡度、坡向影像数据进行气象站点空间数据数值的提取；最后对AOD数据处理，针对京津冀地区创建一个覆盖全区域的5 km×5 km网格，并提取网格中心点的位置坐标，以网格中心点代表该网格的空间位置，利用C#、ArcGIS Engine、Visual Studio 2013程序对MODIS影像数据进行批量处理，通过重采样获取网格中心点AOD的值，利用Java语言程序求出网格中心点AOD数据月均值，再利用ArcGIS10.2对网格中心点AOD数据的月均值进行克里金插值，然后提取气象站点处AOD的值。

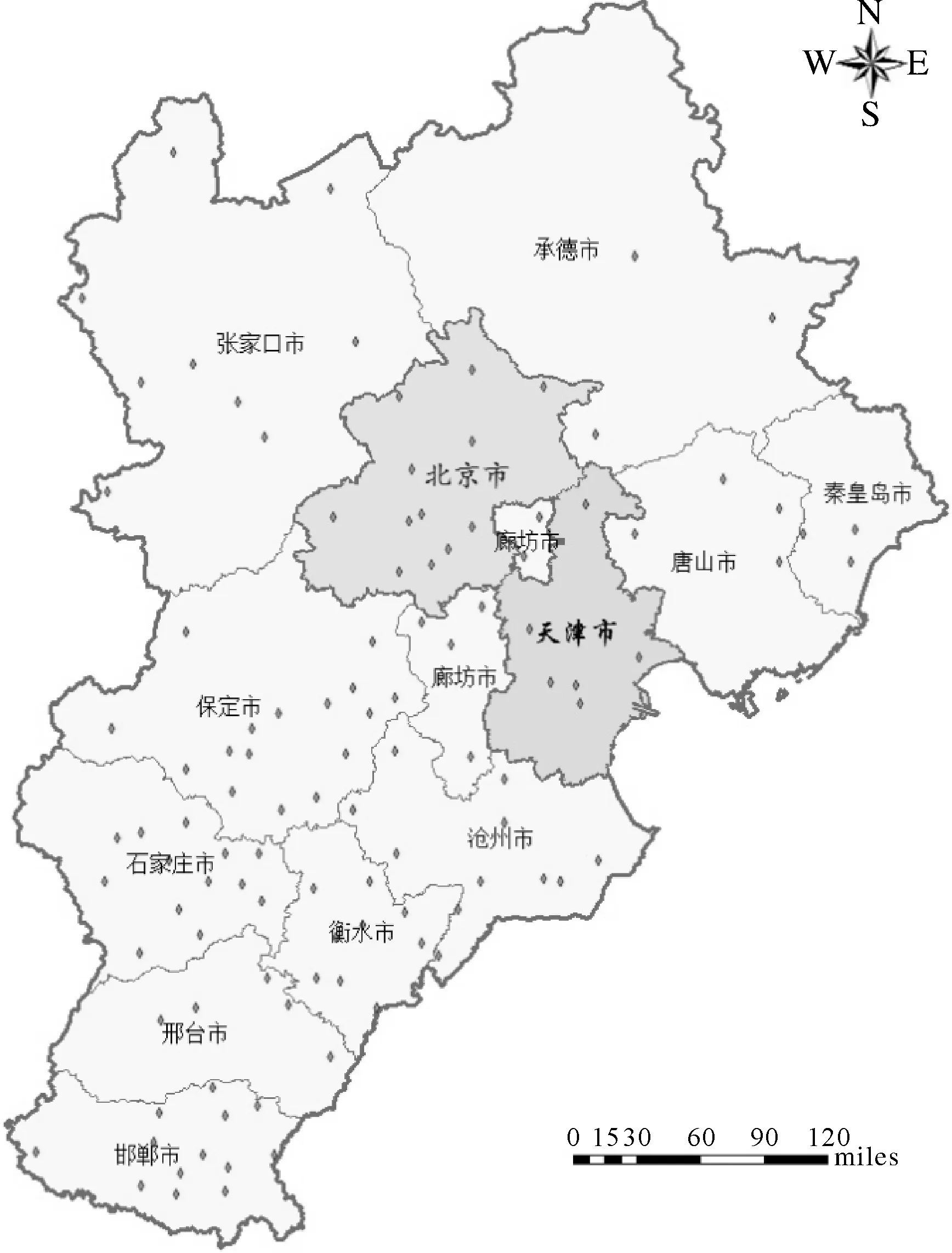
图1 京津冀AOD数据采样点分布

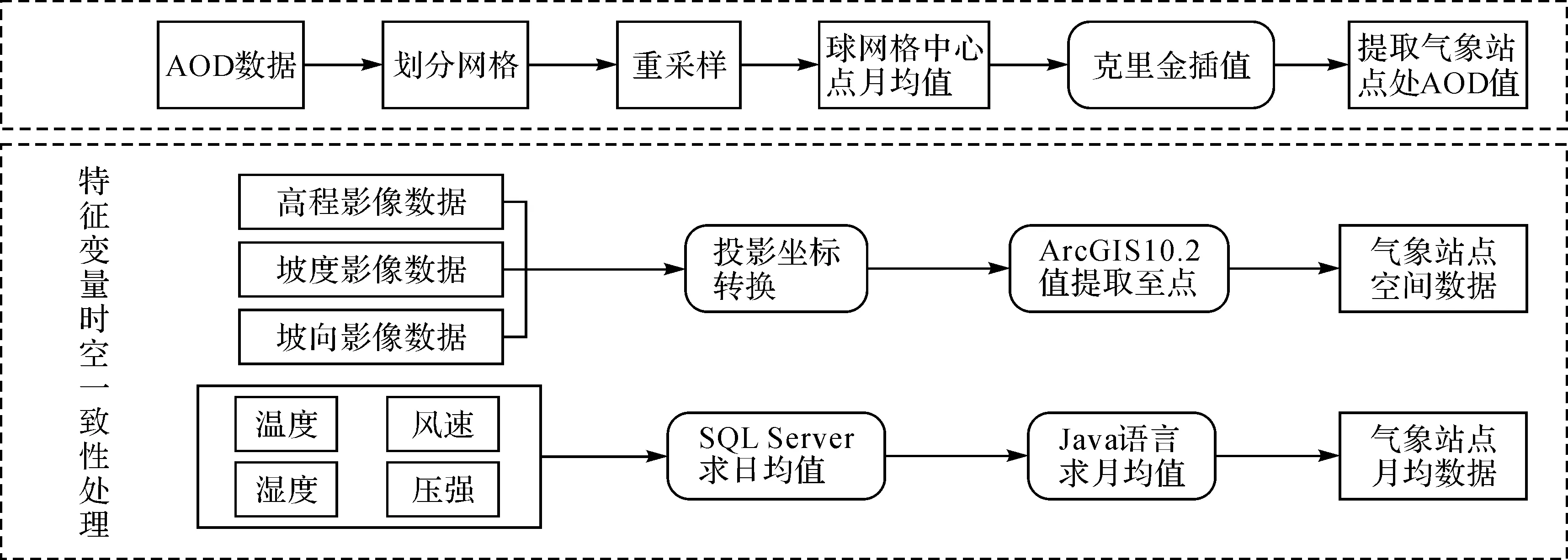
图2 数据预处理流程

2.3.1 影响因素相关性检验

通过相关系数矩阵检验变量间是否存在多重共线性，相关矩阵见表1。由表1可看出，湿度、气压和气温与AOD成正相关，高程、风速、坡度和坡向与AOD成负相关，也可看出本文考虑的这7项指标(湿度、气压、高程、风速、气温、坡度、坡向)均与AOD存在一定程度上的相关性，大部分指标的相关系数均在0.30以上，其中高程和气压与AOD的相关系数更是在0.57以上。可以看出影响主变量的相关变量之间存在多重共线性，通过主成分分析法来消除相关变量之间的多重共线性[19]。(以下数据均保留5位小数)

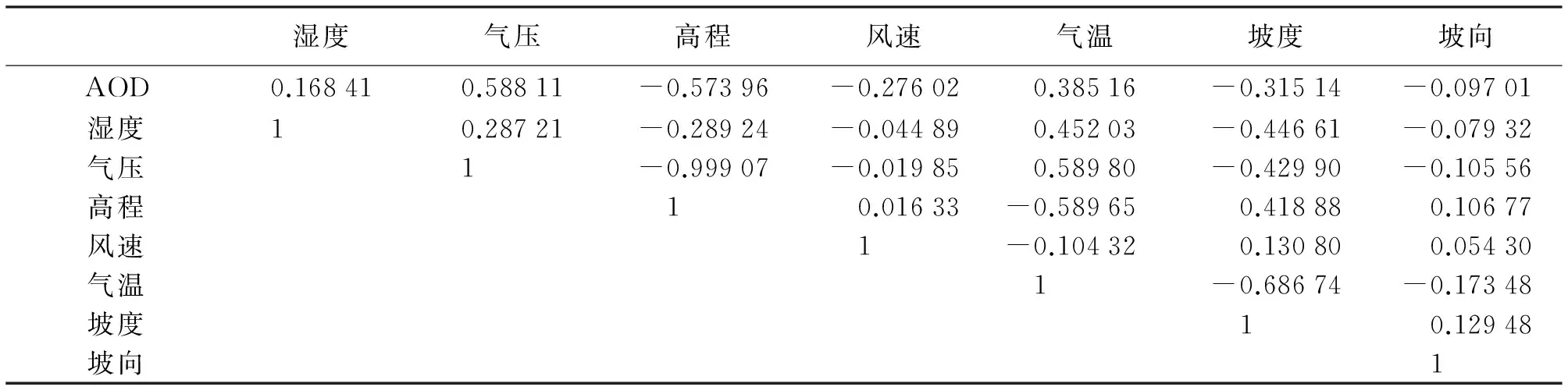
表1 Pearson相关系数

2.3.2 非线性主成分分析

针对AOD数据的预测，对7项指标作非线性主成分分析，本文前3个主成分的特征根及其相应的贡献度与累积贡献度，见表2。(以下数据均保留5位小数)

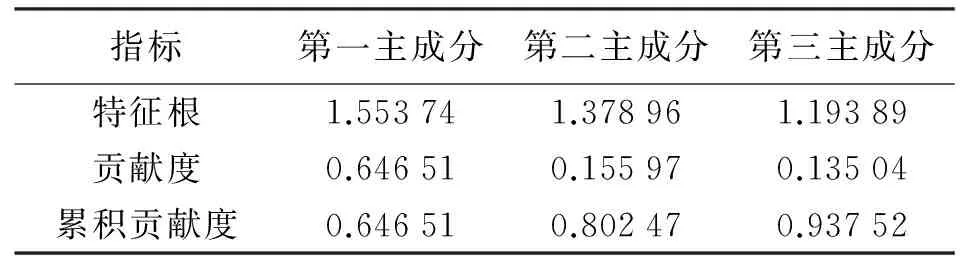
表2 非线性主成分分析结果

由表2的数据预测分析结果可知，第一主成分的特征根、贡献度、累积贡献度分别为1.553 74、0.646 51、0.646 51；第二主成分的特征根、贡献度、累积贡献度分别为1.378 96、0.155 97、0.802 47；第三主成分的特征根、贡献度、累积贡献度分别为1.193 89、0.135 04、0.937 52。前3个主成分的累积贡献度高达93.752%，已接近100%，表明前3个主成分足以代表原始数据的绝大部分信息，因此本文选取前3主成分作为模型的输入变量。

3 结果与分析

为了评估本文研究方法的预测效果，将其与常规的GWR模型进行对比，由表1可知，气压、高程、气温与AOD相关系数在7项指标中最高，以AOD为因变量，以气压、高程、气温为自变量，作GWR回归分析，如图3所示。通过非线性主成分分析后，以第一主成分、第二主成分、第三主成分为自变量，AOD为因变量作PCA-GWR回归分析，如图4所示。同时，分别计算各个模型的平均绝对误差(MAE)、均方根误差(RMSE)、Akaike信息量(AIC)、拟合优度(R2)等4项评价指标，以及模型之间的提升度，计算结果见表3。

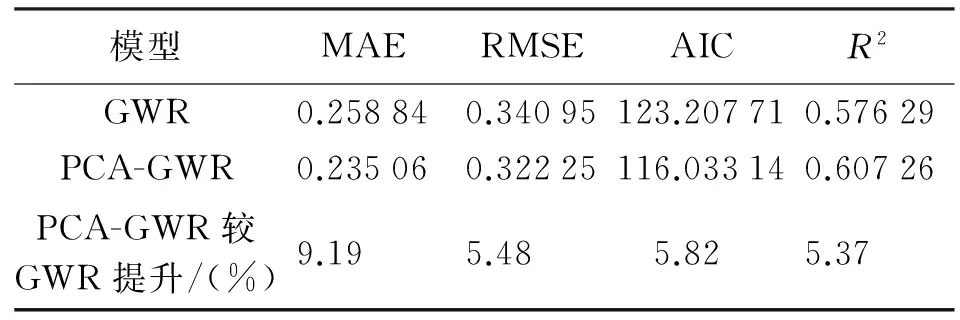
表3 预测结果误差对比

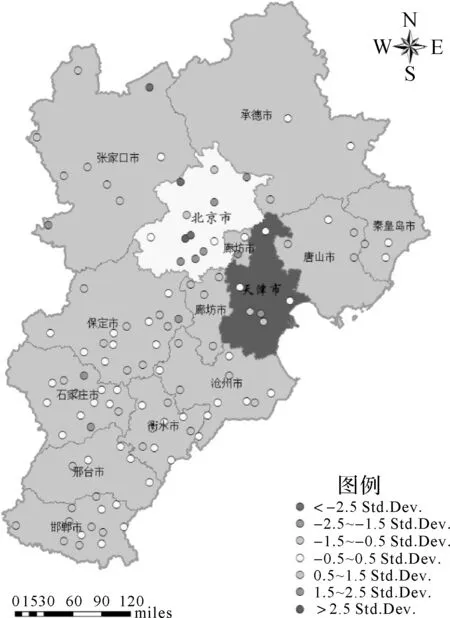
图3 GWR分析结果

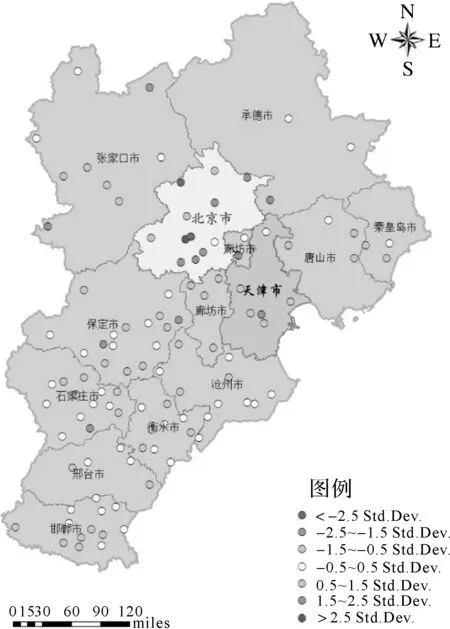
图4 PCA-GWR分析结果

从表3可看出，在4项评价指标MAE、RMSE、AIC、R2中，PCA-GWR方法所得值分别为0.235 06、0.322 25、116.033 14、0.607 26；GWR方法所得值分别为0.258 84、0.340 95、123.207 71、0.576 29。PCA-GWR模型分析所得结果优于常规GWR模型，充分说明本文方法预测结果的优越性。其中，PCA-GWR模型比常规GWR模型的MAE提升9.19%、RMSE提升5.48%、AIC提升5.82%、R2提升5.37%。证明在使用GWR模型预测之前，使用非线性主成分分析法对数据预处理的可行性与优越性；同时，也可以看出PCA-GWR模型比GWR模型的预测效果具有显著的提升。

4 结 论

本文方法在变量个数相同的前提下对AOD浓度的预测精度有明显的提升，说明该方法不仅可以有效地降低计算工作量，减少原始数据信息损失，简化数据结构，还可以消除各个影响因素之间的多重共线性，提高了预测精度。

(1) 相关分析得出湿度、气压和气温与AOD呈正相关，高程、风速、坡度和坡向与AOD呈负相关，这7个影响因素与AOD相关性大小依次为气压>高程>气温>坡度>风速>湿度>坡向。

(2) 通过交叉验证，说明本文采用非线性主成分分析处理后综合指标进行GWR模型预测的精度较高，且减轻了计算量，提高了运算效率。经过对比，本文方法所得4项评价指标MAE、RMSE、AIC、R2均优于常规GWR模型，MAE提升9.19%、RMSE提升5.48%、AIC提升5.82%、R2提升5.37%。

在后续的研究中，将进一步加入其他考虑因子，如污染气体(如CO、SO2)、人类活动、地表覆盖等因子，进而对AOD数据精度进行修正，得到高精度的AOD数据。

参考文献：

[1] 李晓静,高玲,张兴赢,等.卫星遥感监测全球大气气溶胶光学厚度变化[J].科技导报,2015,33(17):30-40.

[2] 刘浩，高小明，谢志英,等.京津冀晋鲁区域气溶胶光学厚度的时空特征[J].环境科学学报，2015，35(5):1506-1511.

[3] 张磊,江洪,陈诚,等.广东省MODIS气溶胶光学厚度时空分布及其影响因素[J].地理空间信息,2017,15(1):46-49.

[4] 王浩洋.遥感反演安徽地区气溶胶光学厚度及其时空特征分析[D].合肥：安徽大学,2015.

[5] 黎丽莉.广东气溶胶光学厚度及穗深空气污染物时空特征和影响因素研究[D].广州：中国科学院研究生院(广州地球化学研究所),2015.

[6] 叶瑜,李秀央,陈坤,等.大气气溶胶光学厚度与大气污染物及气象因素关系的时间序列研究[J].气候与环境研究,2011,16(2):169-174.

[7] 覃文忠.地理加权回归基本理论与应用研究[D].上海：同济大学,2007.

[8] 杨毅.顾及时空非平稳性的地理加权回归方法研究[D].武汉：武汉大学,2016.

[9] 汤庆园，徐伟，艾福利.基于地理加权回归的上海市房价空间分异及其影响因子研究[J].经济地理，2012，32(2):52-58.

[10] HUANG B，WU B，BARRY M.Geographically and Temporally Weighted Regression for Modeling Spatio-temporal Variation in House Prices[J].International Journal of Geographical Information Science，2010，24(3):383-401.

[11] 武文娟，徐京华，时进,等.基于GWR的四川省医院床位数时空分布及其影响因素研究[J].测绘通报，2016(4):49-53.

[12] 董冲亚，康晓平.基于地理加权回归模型的我国女性肺癌发病空间影响因素分析[J].环境与健康杂志，2014，31(9):769-772.

[13] 孙伟伟.基于GWR模型的PM2.5遥感估算模型研究——以长三角为例[C]∥浙江省地理学会.浙江省地理学会2016年学术年会暨浙江省第三届地理名师名校长联盟高峰论坛论文摘要集.杭州:浙江省地理学会，2016:1.

[14] 陈辉，厉青，张玉环,等.基于地理加权模型的我国冬季PM2.5遥感估算方法研究[J].环境科学学报，2016，36(6):2142-2151.

[15] 庞瑞秋，腾飞，魏冶.基于地理加权回归的吉林省人口城镇化动力机制分析[J].地理科学，2014，34(10):1210-1217.

[16] 赵阳阳，刘纪平，徐胜华,等.一种基于半监督学习的地理加权回归方法[J].测绘学报，2017,46(1):123-129.

[17] 覃文忠，王建梅，刘妙龙,等.混合地理加权回归模型算法研究[J].武汉大学学报(信息科学版)，2007，32(2):115-119.

[18] 赵阳阳，刘纪平，张福浩,等.贪心算法的地理加权回归特征变量选择方法[J].测绘科学，2016，41(7):41-46.

[19] 刘蓓.非线性主成分分析法在岩体质量等级分类中的应用[J].水电能源科学,2011,29(12)：78-80.

[20] 高青松,薛付忠.非线性主成分分析中数据非线性特征的检验方法[J].中国卫生统计,2011,28(5):488-491,494.

[21] 檀菲菲,陆兆华.基于NLPCA-GSO可持续发展评价——以环渤海区域为例[J].生态学报,2016,36(8):2403-2412.

[22] 周永正,袁晓辉,周勇.基于非线性主成分神经网络水泥强度预测研究[J].数学的实践与认识,2013,43(3):83-91.

[23] 孙康,耿修瑞,唐海蓉,等.一种基于非线性主成分分析的高光谱图像目标检测方法[J].测绘通报,2015(1):105-108.

[24] FOTHERINGHAM A S，CHARLTON M，BRUNSDON C.Measuring Spatial Variations in Relationships with Geogr Aphically Weighted Regression[M].[S.l.]：Springer，1997：60-63.

[25] CLEVELAND W S.Robust Locally Weighted Regression and Smoothing Scatterplots[J].Journal of the American Statistical Association，1979，74(368):829-836.