非接触式测量获取背部图形的拟合及其验证

吴 尚， 齐 琳， 周双喜， 尚笑梅

(1. 苏州大学 纺织与服装工程学院， 江苏 苏州 215006； 2. 上海纺织集团检测标准有限公司， 上海 200336)

21世纪以来，随着计算机视觉技术的高速发展，针对非接触式自动人体测量技术的研究越来越多。通过非接触式人体扫描仪获得人体轮廓数据，并设计人体曲线尺寸估算算法，根据直接测量到的人体数据建立数学模型进行曲线拟合，进而计算人体曲线尺寸，这种自动测量方法设备简单、占用空间小、成本低、精度基本满足需求，更利于推广和产业化应用。

由于人体为非刚性，在非接触式人体测量技术中确保人体曲线尺寸测量的准确性是最主要的技术难点之一[1]。目前针对非接触式测量的准确性验证方法研究还处于起步阶段：尚笑梅等[2]通过对其建立的服用人体数据库进行大量统计分析，制定了GB/T 30548—2014《服装用人体数据验证方法 用三维测量仪获取的数据》，确定了人体测量的数值验证方法；而对非接触式测量获取的人体图形的准确性验证还鲜有研究报道。

针对以非接触式测量获取人体图像确定标准化图形的验证方法，对样本的轮廓曲线进行拟合处理是核心内容。以大量数据为基础，依照体型分类确定人体各部位的标准曲线模型[3]，即可通过对比来检验样本的拟合曲线是否准确。本文以身高为170 cm成年男性的背部曲线为研究对象，使用非接触式人体测量仪采集样本的背部曲线并对其进行拟合，进而以此为基础对人体测量图形进行验证。

1 人体背部曲线获取方法

人体体型学所定义的背部曲线是指从人体第7颈椎点到骼嵴，沿着脊椎走势紧贴背部皮肤所得到的曲线[4]，其示意图如图1所示。人体背部曲线虽然略微复杂，但其走势大致可分为“一峰一谷”，其中：“一峰”是指从第7颈椎(点1)到肩胛骨下角(点3)间向体外凸起的一部分弧线；“一谷”是指从肩胛骨下角(点3)到骼嵴(点5)间向体内凹陷的一部分弧线。

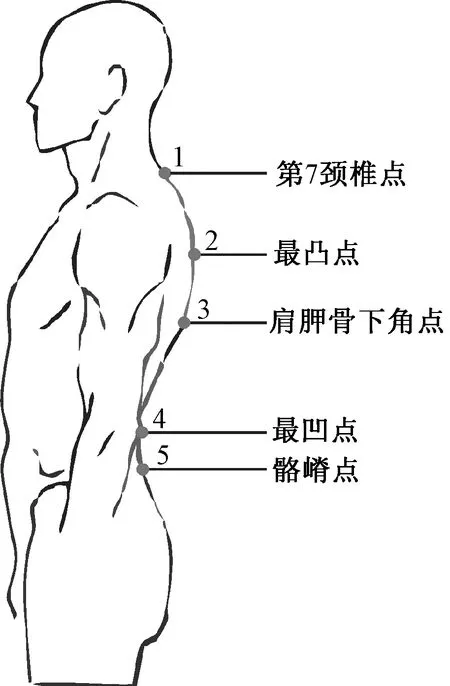
图1 过肩胛人体背部曲线示意图Fig.1 Schematic diagram of male′s back-curve

由此可知，确定背部曲线需要的控制点至少有 5个(见图1)，包括起点第7颈椎点(点1)、最凸点(点2)、肩胛骨下角点(点3)、最凹点(点4)、终点骼嵴点(点5)，控制点越多则模拟出来的曲线越接近真实的背部曲线。为兼顾曲线的精确度和测量的效率，最终确定由起点至终点每隔1 cm取一个标记点。

1.1 贴体曲线采集方法

根据中国《服装号型标准及其应用》规定，选择170/88 A号型成年男性作为样本，使用SIZE STREAM型非接触式人体测量仪采集背部曲线，如图2所示。其中：蓝色曲线为人体表面的点云集合；红色曲线为人体背部曲线。红色曲线右方的点是人体肩胛骨凸出部分，从侧面看均高于人体背部曲线，这是正常体型都会出现的情况。从测量仪所构建的点云人体模型中可透过肩胛骨凸出部分看到背部曲线。将测量仪中提取的背部曲线导入AutoCAD软件，得到人体背部曲线如图3所示。

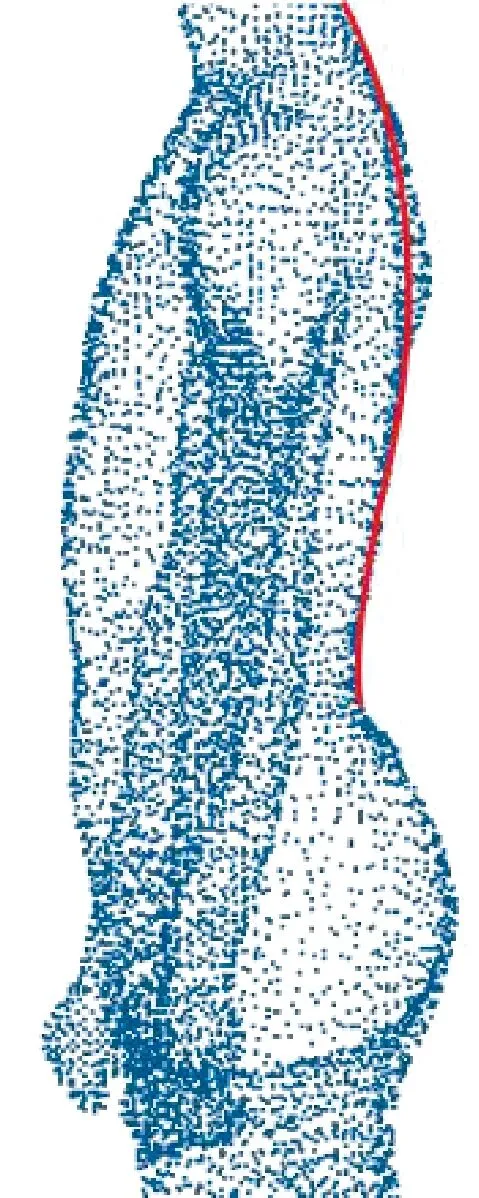
图2 人体背部中心三维模拟图Fig.2 3-D simulation diagram of male′s back-curve

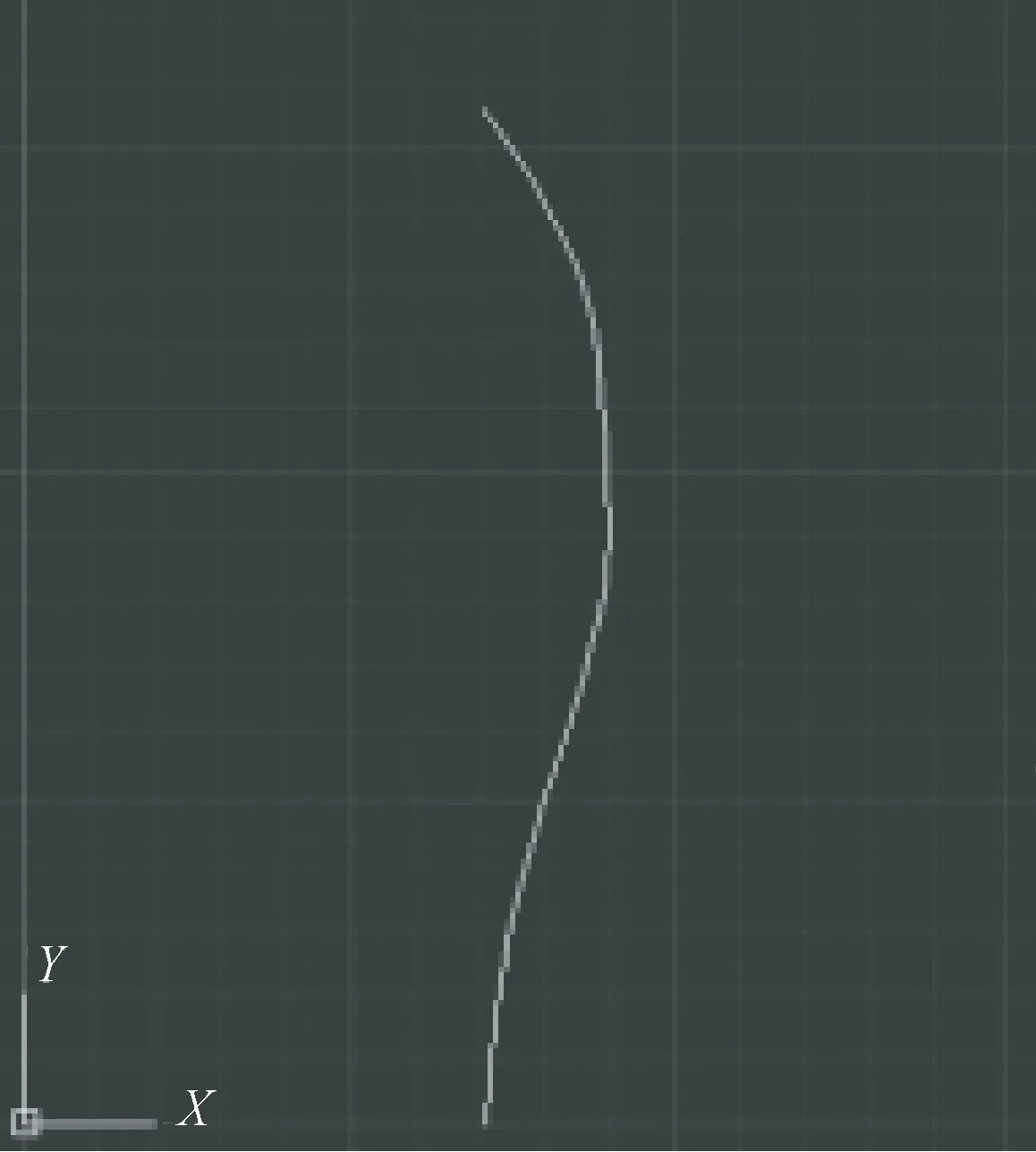
图3 AutoCAD人体背部曲线图Fig.3 Male′s back-curve in AutoCAD

1.2 软尺测量效果模拟

在服用人体尺寸采集时，因不会将真实贴体长度作为该部位的准确尺寸，而是使用软尺围住人体弧线测量其外接曲线的弧长[5]，因此，需要在获取的背弧曲线上模拟软尺的走势，构建一条圆顺的外接曲线，通过测量该曲线的弧长即可得到软尺测量的背长值。

考虑到背弧曲线的凹凸性[6]，而B样条曲线可通过逼近任意数目的控制点来拟合曲线[7]，该曲线可满足人体背部曲线特征。根据背部曲线的走势，模拟软尺曲线必须经第7颈椎点、最凸点、肩胛骨下角以及骼嵴点，可构成三次B样条曲线。使用AutoCAD拟合的背部曲线效果如图4所示，白色曲线为原贴体曲线，红色曲线为模拟软尺曲线。

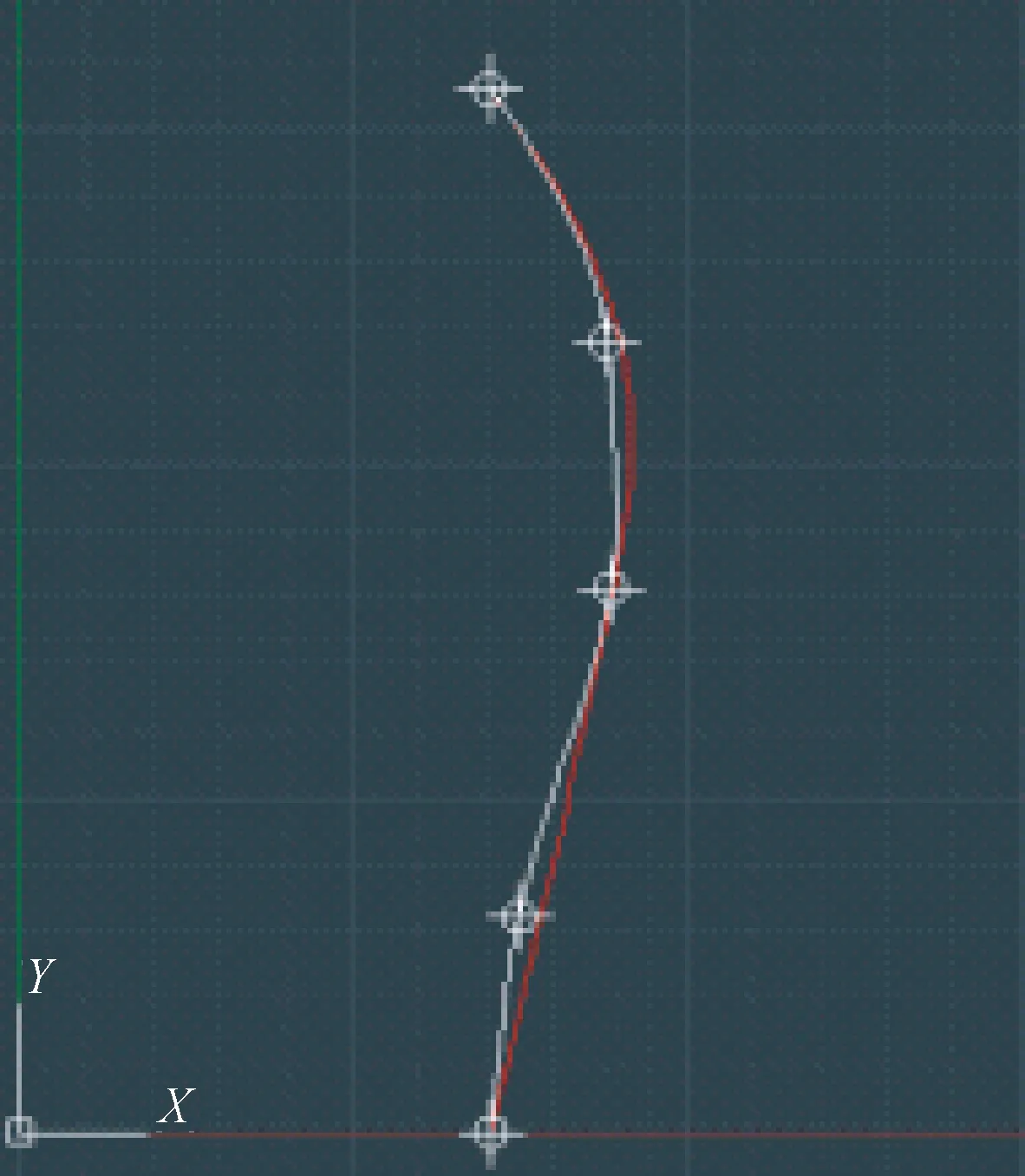
图4 AutoCAD模拟软尺曲线图Fig.4 Schematic diagram of tape measuring with AutoCAD

将AutoCAD拟合曲线的弧长与样本手工测量值进行对比，平均误差约为0.3 cm，远低于服装背长尺寸的档差，模拟软尺测量的效果比较理想，符合服用人体测量的需求。

2 人体背部曲线拟合方法

获取背部的模拟软尺曲线以后，就可进行曲线函数的拟合。前期研究已表明，对于圆顺曲线中截取的等距离点集，采用最小绝对残差(LAR)的稳健回归分析法[8]进行最小二乘拟合，多项式函数拟合的结果要比对数函数和指数函数更好，因此，本文对比了对数函数和多项式函数拟合效果，并对拟合函数的次数对拟合优度的影响进行更深层次的讨论。

2.1 等距离点集截取

将AutoCAD中模拟的软尺曲线以第7颈椎点为起点、以骼嵴点为终点，截取间距为1 cm的等距离的点，并将所有点的坐标记录到Excel表格中，准备导入拟合程序。

2.2 函数拟合方法

将等距离点集的坐标导入Origin中，考虑到多项式函数图像的特征，将原本的横纵坐标交换，获得待拟合的散点图如图5所示。设置不同次幂的函数对散点图进行拟合。

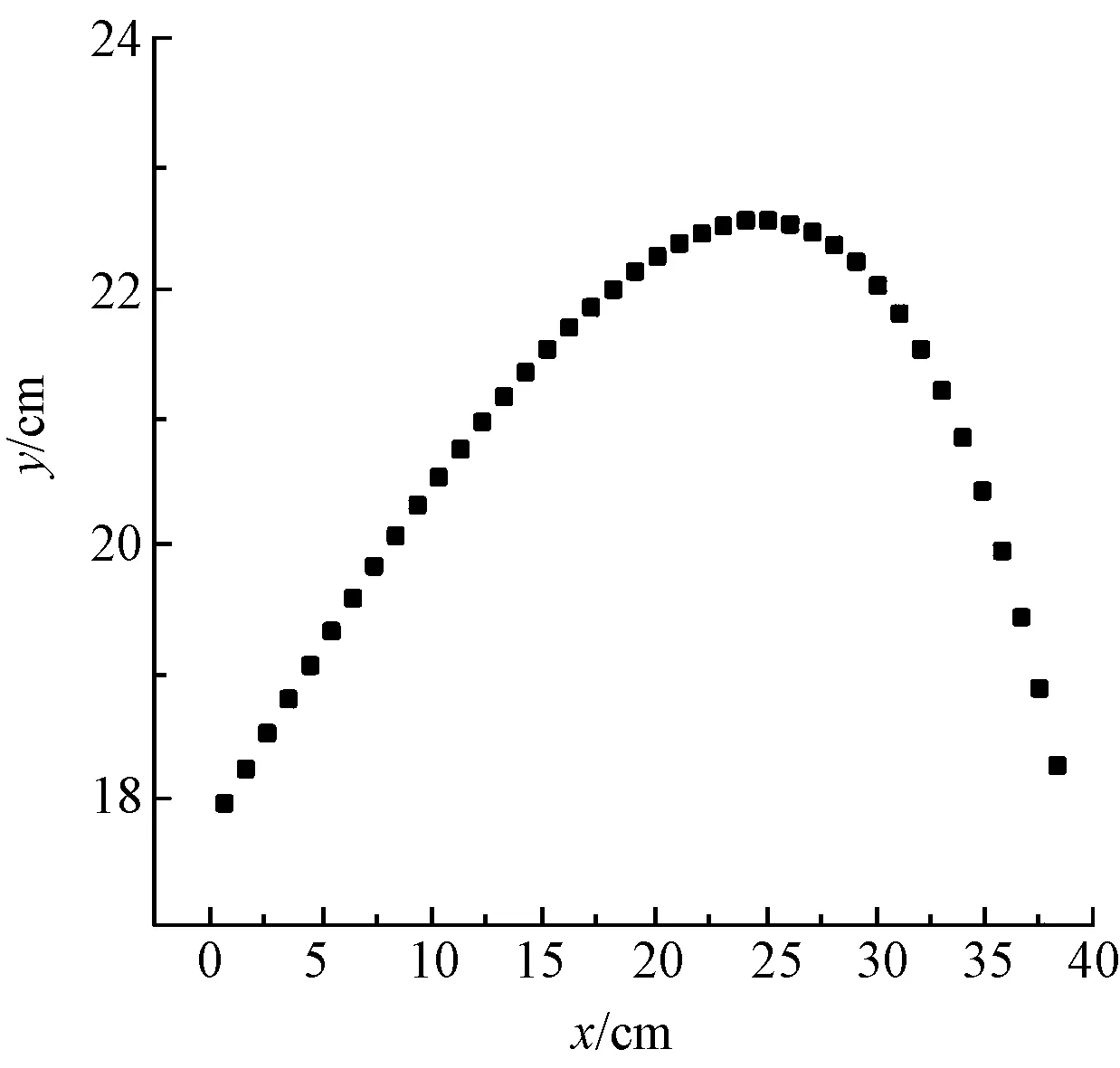
图5 人体背部曲线散点图Fig.5 Scatter diagram of male′s back-curve

3 拟合函数确定

经过Origin函数拟合，分别得到对数函数以及二次、三次、四次多项式函数的拟合效果，其拟合结果如图6～9所示。

图6 对数函数拟合结果Fig.6 Logarithmic function fitting result

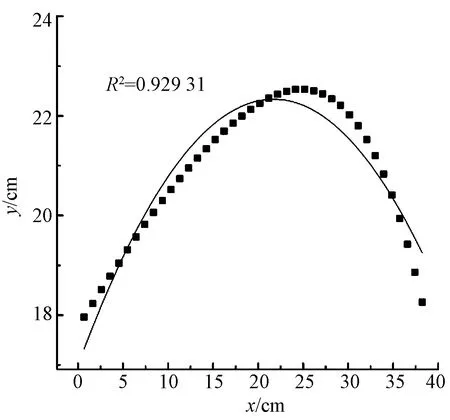
图7 二次多项式拟合结果Fig.7 Quadratic polynomial function fitting result

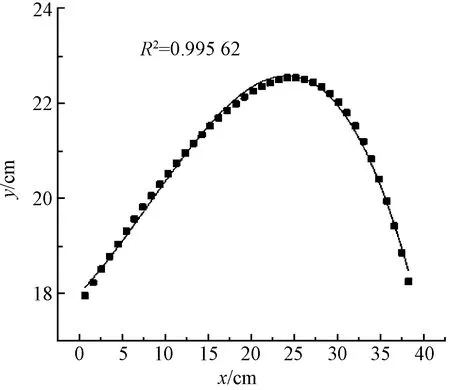
图8 三次多项式拟合结果Fig.8 Cubic polynomial function fitting result

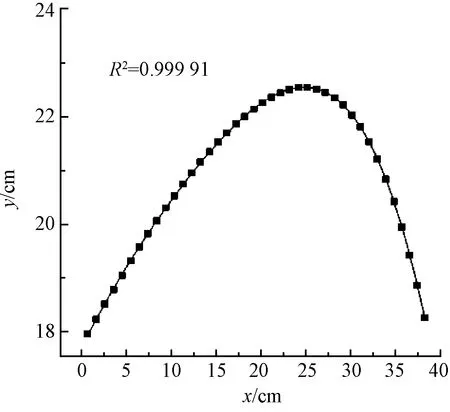
图9 四次多项式拟合结果Fig.9 Four times polynomial function fitting result

根据拟合结果可知，多项式拟合的效果非常理想，综合考虑拟合优度及函数表达式的简洁性，决定选用三次多项式作为标准拟合函数。将25组样本数据根据拟合函数求出弧长，与手工测量值进行对比，平均误差仅为0.57 cm左右，远低于 GB/T 1335.1—2008《服装号型 男子》中对背长档差规定的2 cm[9]，其准确性较高，符合服用尺寸测量的需求。

4 拟合曲线准确性验证

经过对25组样本数据的拟合分析，将170/88A男性背部曲线模拟软尺测量的标准曲线函数表达式确定为：

f(x)=-0.000 33x3+0.008x2+0.19x+18

为检验标准拟合曲线的准确性，需要利用验证组数据进行对比。由于同号型的人体曲线形状在误差范围内近乎相似，可将标准拟合曲线参数化，根据样本曲线相关的基本直线长度数据与标准曲线对应，进行参数函数的比例放缩，从而推算出样本曲线的长度。将样本曲线的推算长度与拟合长度进行对比，根据其误差大小即可判断标准拟合曲线是否准确[10]。

人体背部曲线所对应的基本直线长度数据为背长(直)和胸厚，此处背长(直)定义为人体第7颈椎点到腰围平面的直线距离，而胸厚定义为人体胸部最外侧切面到人体背部最外侧切面的直线距离；因此，首先检验人体背部曲线长度与背长(直)和胸厚之间的相关性，将验证组数据导入SPSS中进行相关性分析，结果如表1所示。可以看出，背长(直)与背部曲线长具有相关性但不显著，而胸厚与背部曲线长在0.01水平显著相关。

表1 相关性分析结果Tab.1 Result of correlation analysis

由此可知，人体背部曲线长度和背长(直)、胸厚之间具有相关性，可以通过背长和胸厚推算背部曲线长度。以标准曲线函数为参照函数，将y=f(x)转换为参数方程：

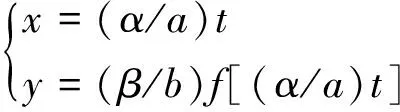
式中：t为参数；α、β分别为所求样本的背长(直)和胸厚；a、b为参照函数所对应背部曲线的背长(直)和胸厚。

在此基础上通过对x、y进行比例缩放，再对参数方程进行定积分求弧长，即可推算出所求样本的背长(弧)。

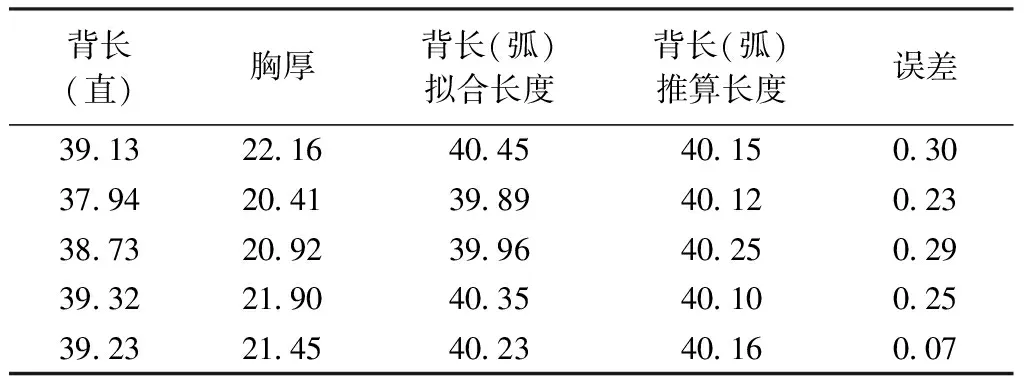
将验证组的5个样本数据采用上述方法进行推算，其对照结果如表2所示。

表2背长(弧)推算与拟合结果对照表

Tab.2Comparisonresultofvalidationgroupcm

背长(直)胸厚背长(弧)拟合长度背长(弧)推算长度误差39132216404540150303794204139894012023387320923996402502939322190403540100253923214540234016007

可见推算结果误差较为稳定，均小于1 cm，可靠性较高，在同号型范围内，通过拟合确定的标准人体背部曲线函数的准确性符合要求。

5 结 论

本文通过对170/88A号型青年男性的背部曲线进行拟合分析，得出以下结论。

1)考虑函数表达式简洁性和拟合曲线弧长误差后，确定采用三次多项式函数作为拟合函数，其拟合优度达到0.995 62。根据拟合函数计算得到的背部曲线弧长与实际测量长度的平均误差小于1 cm，远低于服装号型中背长档差的规定，符合服装用人体数据的精确度要求。

2)通过多次拟合实验确定了170/88A体型的青年男性背部曲线标准参照函数，为f(x)=-0.000 33x3+0.008x2+0.19x+18。

3)人体背部曲线长度与背长(直)、胸厚这2个直线尺寸具有相关性，以标准参照函数为基础，通过参数函数比例放缩法，推算出同号型样本的背部曲线长度，经对比样本的曲线拟合长度和比例推算长度误差小于1 cm，证明该曲线拟合的准确性符合要求。

4)由于采集样本的范围和数量有限，本文研究仅限于170/88A体型的成年男性背部曲线，要建立完善的标准化人体测量图形验证方法，还需要将人群按体型分类后分别进行大量的拟合计算，对本文的研究成果进行检验。

FZXB

参考文献：

[1] 叶璇, 肖平, 白小菡, 等. 三维人体测量技术标准比较[J]. 纺织科技进展, 2013, 20(5): 61-64.

YE Xuan, XIAO Ping, BAI Xiaohan, et al. Compare of 3-D body scanning technique standard[J]. Progress in Textile Science & Technology, 2013, 20(5): 61-64.

[2] 田亚楠, 贺莉文, 尚笑梅. 不同测量方法对测量值精确度的影响分析[J]. 北京服装学院学报(自然科学版), 2016, 36(4): 25-31.

TIAN Ya′nan, HE Liwen, SHANG Xiaomei. Influence of measurement methods on the accuracy of measured data[J]. Journal of Beijing Institute of Fashion Technology(Natural Science Edition), 2016, 36(4): 25-31.

[3] 倪世明, 金娟凤, 庞程方. 基于纵向轮廓曲线的青年女性体型细分研究[J]. 纺织学报, 2014, 35(8): 87-93.

NI Shiming, JIN Juanfeng, PANG Chengfang. Research of young female somatotype based on longitudinal profile curves[J]. Journal of Textile Research, 2014, 35(8): 87-93.

[4] 尚笑梅, 卢晨, 王辉. 基于自动测体的围度曲线拟合模型[J]. 纺织学报, 2010, 31(4): 128-131,138.

SHANG Xiaomei, LU Chen, WANG Hui. Human body circumference curve fitting model based on automatic measurement[J]. Journal of Textile Research, 2010, 31(4): 128-131,138.

[5] 卢晨, 王辉, 尚笑梅. 人体胸围曲线的拟合方法[J]. 苏州大学学报(工科版), 2009, 29(3): 47-50.

LU Chen, WANG Hui, SHANG Xiaomei. Fitting methods for size of human bodies chest circumfe-rence[J]. Journal of Soochow University (Engineering Science Edition), 2009, 29(3): 47-50.

[6] 隽峰, 黎小间. B样条曲面拟合方法在人体测量中的应用[J]. 计算机应用研究, 2007, 24(5): 183-185.

JUAN Feng, LI Xiaojian. Application of B-spline fitting surface to measure of body[J]. Application Research of Computers, 2007, 24(5): 183-185.

[7] TULI M, REDDY N V, SAXENA A. Constrained shape modification of B-spline curves[J]. Computer-Aided Design and Applications, 2006, 3: (1-4):437-446.

[8] VARA R D L, AGUIRRE V M. Robust regression methods for the analysis of unreplicated factorials[J]. Lecture Notes in Engineering and Computer Science, 2009, 2177(1).

[9] 蔡兰, 厉旗, 尚笑梅. 基于衬衫部件重构的纸样设计方法[J]. 纺织学报, 2015, 36(8): 116-120.

CAI Lan, LI Qi, SHANG Xiaomei. Pattern design method based on reconstruction of parts in blouse[J]. Journal of Textile Research, 2015, 36(8): 116-120.

[10] 高佩佩, 乐逸朦, 尚笑梅. 服用人体控制部位截面模型研究综述[J]. 现代丝绸科学与技术, 2015, 22(6): 234-236.

GAO Peipei, LE Yimeng, SHANG Xiaomei. A review on the research of human station′s section model for garment[J]. Modern Silk Science & Technology, 2015, 22(6): 234-236.