基于反馈系统FXLMS的非线性主动降噪

苏雨，卢剑伟，邵浩然

（合肥工业大学机械工程学院，安徽 合肥 230009）

0 引言

家用空调器室内柜机噪声问题一直是各大家电企业关注的问题，被动降噪技术可以消除大部分的中高频噪声，但却对更影响人们身心健康的低频噪声束手无策[1-3]。主动降噪则对低频噪声消噪有着较优的效果，并且可以在一定的窄带频段上自适应消噪而不是单一频率上进行消噪[4]。家用空调器室内柜机内部空间小、声场复杂，所导致系统声反馈问题和参考噪声不易获得问题限制了其可应用的主动降噪系统的结构为反馈型系统[5-7]。

反馈型主动降噪系统基本原理是对初级噪声进行估计，并用这个估计代替实际的噪声信号作为主动降噪系统的参考信号，整个系统降噪性能取决于次级通道估计的准确度[8-9]。基本的自适应滤波算法的滤波器都是线性滤波器，对次级通道的非线性部分难以很好地跟踪、拟合和预测。且反馈型系统稳定性较前馈型差，当误差过大时反馈型系统易失去降噪效果[10-11]。

本文为了提高反馈型系统的性能以取得更大的降噪量，引入Volterra级数，并对其进行截断和简化成二阶非线性滤波器。利用其非线性特性和记忆性，对次级通道传递函数非线性部分进行跟踪、拟合和预测[12-15]。对比次级通道为不同系统时基于非线性滤波器和线性滤波器的反馈自适应算法的收敛速度和降噪性能。针对某公司家用空调器室内柜机的低频段噪声的特性，基于德州仪器的TMS320VC5509 DSP搭建硬件系统，试验验证了引入非线性滤波器后的降噪量有所提高。

1 问题简述

对某品牌家用空调器室内柜机进行单机运行噪声测试，得到其低速工况和高速工况下噪声频谱图。

图1 低速工况噪声频谱图Fig.1 Noise spectrum of low speed working condition

图2 高速工况噪声频谱图Fig.2 Noise spectrum of high speed working condition

可以看出家用空调器室内柜机的噪声分布频域较广，且低频段噪声能量较大。传统的被动降噪方法对低频消噪效果不好且只能针对某个频率。工况变化时，噪声频谱随之变化，传统降噪方法无法随着工况的改变而自适应降噪。

2 算法原理

2.1 非线性Volterra滤波器

对于单一输入x( n)、单一输出y( n)的非线性连续时不变系统，其输入输出的响应可以用Volterra级数来表示：

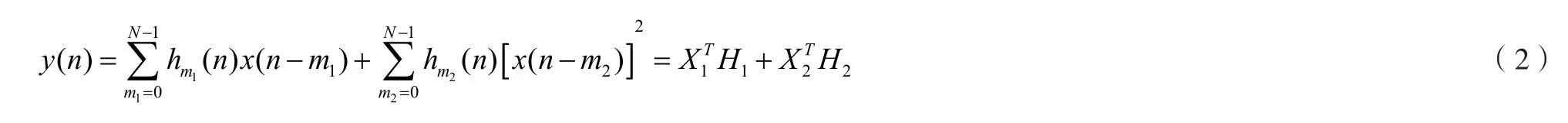
对其进行离散余弦变化并写成矩阵形式：

对比常用的FIR滤波器的表达式（4），简化后的二阶Volterra滤波器比FIR滤波器多了非线性的平方项，保留了其非线性特性。

2.2 反馈系统FXLMS算法

在LMS算法的基础上，FXLMS算法考虑了扬声器和误差麦克风之间的次级通道，补偿了次级通道中扬声器和误差麦克风之间的信号不同步问题。基于FXLMS算法的反馈系统噪声主动控制原理如图3所示。

图3 FXLMS反馈系统框图Fig.3 Block diagram of FXLMS feedback system

反馈型系统FXLMS的基本原理是对初级噪声进行估计，并用这个估计代替实际的噪声信号作为主动降噪系统的参考信号x( n)。反馈型系统的特点是不存在初级通道，只有次级通道。对于反馈型FXLMS算法，如果次级通道估计准确即则整个算法的性能取决于d( n)预测准确与否，也就是次级通道的建模精度。其中：

其中，自适应滤波器的输入、输出为：

自适应滤波器的系数更新为：

将简化的二阶Volterra滤波器来代入反馈型FXLMS算法中得到反馈型非线性FXLMS算法，其滤波器更新迭代变为：

自适应的输出也变为：

3 仿真及结果分析

我们设计次级通道为不同的类型，对反馈型非线性FXLMS算法和反馈型线性FXLMS算法进行次级通道建模性能、算法性能仿真模拟分析。通常使用均方误差（NMSE）作为自适应算法性能的检验指标，对比曲线的下降速度和收敛值可以直观的看出算法收敛速度和降噪性能。

首先针对次级通道为线性和非线性的两种情况进行仿真。设定两个滤波器长度均为16，输入的信号x( n)为方差为1均值为0的高斯白噪声信号。次级通道为线性系统：

次级通道为线性的时候，对比NMSE仿真图两个曲线几乎完全重合。可以直观的看出两个滤波器的性能相当，估计的均方误差收敛速度和收敛值都无明显差别。

次级通道为非线性系统：

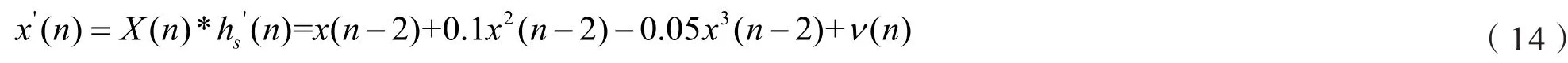
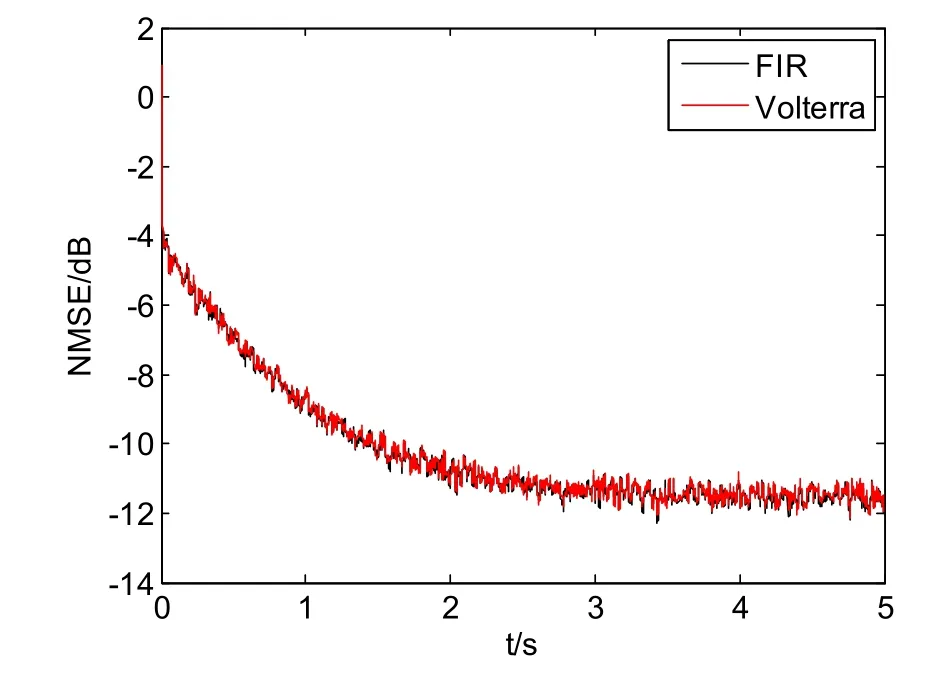
图4 次级通道为线性的NMSE性能比较Fig.4 NMSE comparison of linear secondary channel

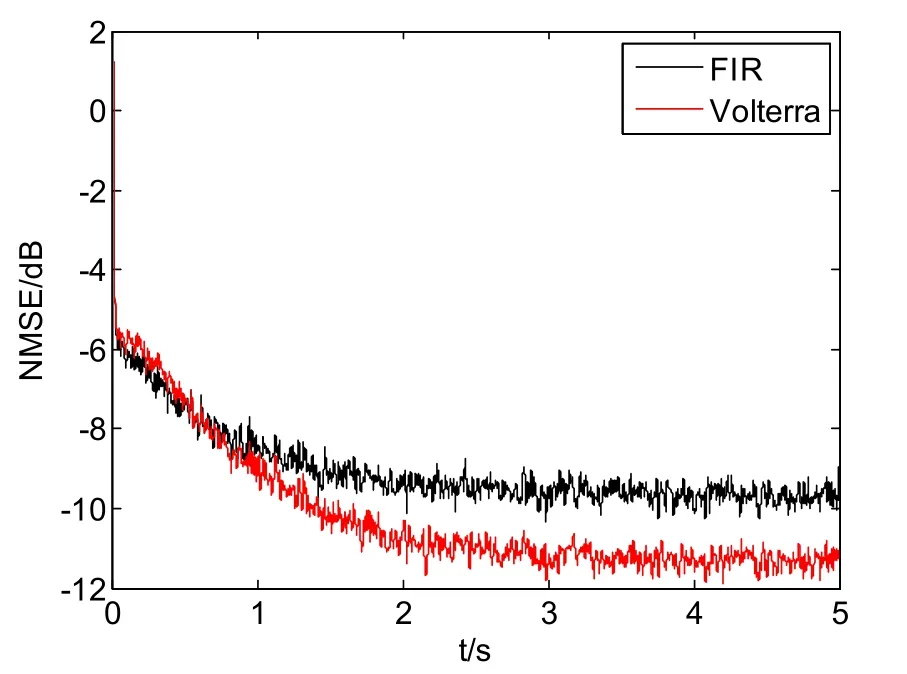
图5 次级通道为非线性的NMSE性能比较Fig.5 NMSE comparison of nonlinear secondary channel

次级通道为非线性的时候，对比NMSE仿真图，可以看出Volterra滤波器的均方误差收敛速度要快于FIR滤波器，且NMSE稳定时值要更低。说明Volterra滤波器的非线性性能要优于FIR滤波器。对比次级通道为线性、非线性时，两个滤波器各自的NMSE性能可以看出，次级通道为非线性时FIR滤波器的建模精度降低、从而算法性能也相应变差，而对Volterra滤波器来说则几乎没有影响。

实际工程中常遇到的系统通常很少用线性和非线性进行划分，而是根据其在控制工程方面的特性进行划分。一般根据系统的零点都在单位圆内还是有一个或者多个在单位圆外，将系统分为最小相位系统和非最小相位系统。下面对次级通道为最小相位系统和非最小相位系统两种情况进行仿真和对比分析。次级通道为最小相位系统时：

次级通道为非最小相位系统时：

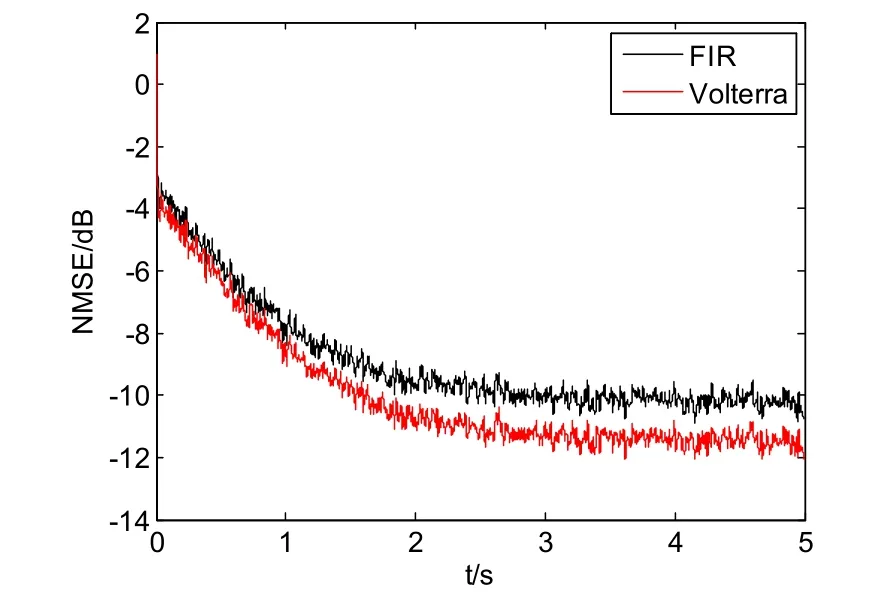
图6 次级通道为最小相位的NMSE性能比较Fig 6 NMSE comparison of minimum phase secondary channel

图7 次级通道为非最小相位的NMSE性能比较Fig.7 NMSE comparison of non-minimum phase secondary channel

次级通道为最小相位和非最小相位时，Volterra滤波器的建模精度以及算法性能都要优于FIR滤波器，且非最小相位时NMSE稳定时差值要更大一点。次级通道为非最小相位时，系统中存在着迟滞环节，相较于最小相位系统，两滤波器的收敛速度都变慢且NMSE稳定值变高，综合性能都变差。可以看出系统的迟滞环节对系统的跟踪预测准确度来说有较大的影响。

综合四种仿真情况，可以对比分析出引入简化的二阶Volterra滤波器的反馈FXLMS算法性能较FIR滤波器要更优，对系统的非线性和迟滞环节都有较优的跟踪预测性能。

4 试验验证

基于德州仪器的TMS320VC5509 DSP搭建了如图8所示的硬件系统，布置在了家用空调器内部区域。我们用计算机模拟前面测试的室内柜机噪声源低频段噪声特性，控制扬声器播放30 Hz 、110 Hz、170 Hz、220 Hz、280 Hz、330 Hz、390 Hz多个单频正弦噪声的合成噪声，分别采用反馈型非线性FXLMS算法和反馈型线性FXLMS算法来进行降噪。设计两滤波器长度均为16，目标降噪频段均为100 Hz至 400 Hz。

图8 主动降噪硬件系统图Fig.8 Active noise control hardware system

图9 柜机降噪试验测试图Fig.9 Noise reduction test picture of indoor unit

测试试验得到了降噪前后对比图。

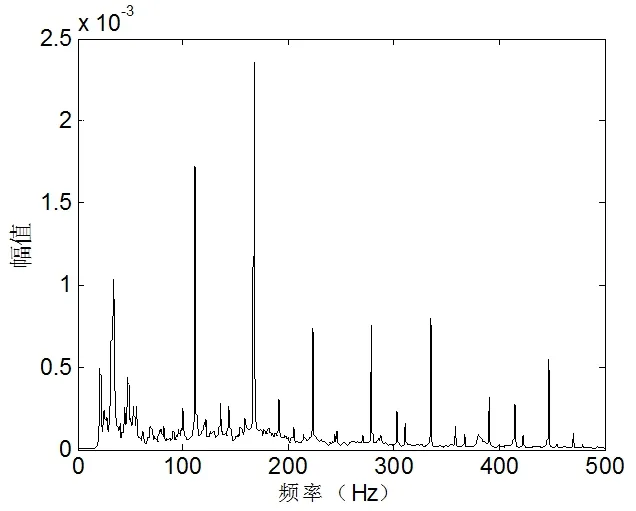
图10 噪声频谱图Fig.10 Noise spectrum

图11 FIR反馈FXLMS算法降噪后频谱图Fig.11 Noise spectrum of noise reduction after feedback FIR-FXLMS

图12 Volterra反馈FXLMS算法降噪后频谱图Fig.12 Noise spectrum of noise reduction after feedback Volterra-FXLMS

对我们设计的降噪频段的A计权数值进行计算统计，结果如表1所示。

表1 降噪试验结果Table 1 Noise reduction test result

对图8和表1中的测试结果进行分析对比，我们可以看出在100 Hz至400 Hz的设计降噪频段内，降噪后的频谱图中的突出频率波峰明显较降噪前减小。Volterra反馈FXLMS算法的降噪性能在整个设计频段都要优于FIR反馈FXLMS算法。FIR反馈FXLMS算法总频段降噪量较小为1.2 dB，在有些频段甚至出现了增加现象。Volterra反馈FXLMS算法则降噪性能较优，总频段降噪量为7.7 dB，设计频段内都产生了一定的降噪量，特别是250 Hz至400 Hz降噪量比较大。250 Hz至400 Hz频段为设计频段内的较高频段，相比低频来说人耳较为敏感且较易引起人的烦躁感，主观降噪声品质更好。

5 结论

根据前面的模拟仿真工作和试验验证，我们可以得出两个结论：① 在系统的非线性和迟滞环节的跟踪预测方面，引入Volterra非线性滤波器后的反馈FXLMS算法较FIR滤波器都有较优的性能。② 针对家用空调室内柜机低频噪声，非线性反馈FXLMS主动降噪系统降噪量明显比线性反馈FXLMS主动降噪系统更高。

[1] 李晓阳. 家用空调器噪音识别分析及控制关键技术研究[D]. 合肥：合肥工业大学, 2015.LI Xiao-yang. Research on key technologies of noise identification and control of household air conditioner[D]. Hefei: Hefei University of Technology, 2015.

[2] 卢剑伟. 家用空调器机械噪声源识别研究[J]. 合肥工业大学学报(自然科学版), 2006, 29(1): 73-76.LU Jian-wei. Identification of the mechanical noise source in domestic air conditioners[J]. Journal of Hefei University of Technology, 2006,29(1): 73-76.

[3] 于坤鹏, 陈天宁, 王小鹏. 吸声棉对声子晶体禁带特性的影响研究[J]. 新型工业化, 2013, 3(4): 1-7.YU Kun-peng, CHEN Tian-ning, WANG Xiao-peng. Effect of the glass wool on the band gap of phononic crystal[J]. The Journal of New Industrialization, 2013, 3(4): 1-7.

[4] 陈克安. 有源噪声控制[M]. 北京: 国防工业出版社, 2014: 11.CHEN Ke-an. Active Noise Control[M]. Beijing: National Defense Industry Press, 2014: 11.

[5] HU J, HSIAO T. Adaptive Feedforward Active Noise Cancellation in Ducts Using the Model Matching of Wave Propagation Dynamics[J].IEEE Transactions on Control Systems Technology, 2012, 20(5): 1351-1356.

[6] ROMEU J, SALUENA X, JIMENEZ S, et al. Active noise control in ducts in presence of standing waves. Its influence on feedback effect[J].Applied Acoustics, 2001, 62(1): 3-14.

[7] 袁宇鹏, 杨璐溦, 刘洋. 自适应神经模糊推理系统在汽车发动机转速预测中的应用[J]. 新型工业化, 2014, 4(12): 31-35.YUAN Yu-peng, YANG Lu-wei, LIU Yang. Application of adaptive neural-network-based fuzzy inference system in vehicle engine speed prediction[J]. The Journal of New Industrialization, 2014, 4(12): 31-35.

[8] KUO S M, VIJAYAN D. Adaptive feedback active noise control[C]//Noise Con 1994: Proceedings of the 1994 National Conference on Noise Control Engineering, 1994(6): 473-478.

[9] ARDEKANI I T, ABDULLA W H. Effects of imperfect secondary path modeling on adaptive noise control system. [J]. IEEE Transaction on Control Systems Technology, 2012, 20(5): 1252-1262.

[10] WANG T, Gan W S. Stochastic analysis of FXLMS-based internal model control feedback active noise control systems[J]. Signal Processing,2014, 101(C): 121-133.

[11] LUO L, Sun J, HUANG B. A novel feedback active noise control for broadband chaotic noise and random noise[J]. Applied Acoustics, 2017,116: 229-237.

[12] BOYD S, CHUA L O, DESOER C A. Analytical Foundations of Volterra Series[J]. Ima Journal of Mathematical Control & Information, 1984,1(3): 243-282.

[13] 房媛媛, 李亚安, 崔琳, 等. 基于Volterra级数的自适应水声信号预测方法研究[J]. 兵工学报, 2013, 34(9): 1173-1179.FANG Yuan-yuan, LI Ya-an, CUI Lin. Research on prediction of underwater acoustic signals based on volterra adaptive filter[J]. Acta Armamentarii, 2013, 34(9): 1173-1179.

[14] KOH T, POWERS E J. Second-order Volterra filtering and its application to nonlinear system identification[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1985, 33(6): 1445-1455.

[15] SCHETZEN M. Nonlinear System Modelling and Analysis from the Volterra and Wiener Perspective[M]//Block-oriented Nonlinear System Identification. Springer London, 2010: 13-24.