基于模态理论的白车身静刚度计算方法
张文韬 王震虎 方向东 杨续跃 李落星 王万林
1.中南大学材料科学与工程学院,长沙,410083 2.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100823.重庆长安汽车商用车研究院,重庆,400023
0 引言
白车身的弹性体模态和静刚度是衡量汽车基础性能的两项重要指标,在很大程度上影响着整车的噪声、振动与声振粗糙度(noise, vibration and harshness,NVH)性能,安全性,操纵稳定性,耐久性,以及燃油经济性[1]。白车身的低阶模态设定(一阶弯曲、扭转模态等)要尽量避开发动机怠速时的激励频率,以免汽车行驶时发生共振;而白车身的弯曲、扭转刚度则分别反映了汽车在承受载荷时的抗弯变形能力以及在凹凸不平路面行驶时的抗扭变形能力。整车性能目标的设定以及车身结构的设计开发中,白车身的静刚度和低阶模态是两个非常重要的参数。
国外在研究线性系统静刚度与模态、动刚度的关联性时,一般通过试验获取系统的频率响应函数(frequency response function, FRF),再利用构建的柔度矩阵对静刚度进行计算。GRIFFITHS等[2]研究了简单结构的弹性体模态和静刚度之间的关系,并通过试验和有限元仿真对此加以验证;PASHA等[3-5]通过对自由边界的频率响应函数的测定,成功估算了简单矩形板的弯曲刚度和扭转刚度;WAHYUNI等[6]通过理论推导,探明了简单性系统的静态刚度与模态刚度之间的关系,并通过仿真手段加以验证。以上研究均是将一些简单的线性结构(如简支梁、矩形框架以及矩形板)作为研究对象,并未将其推广至工程中的大型复杂线性系统。为此,HELSEN等[7]提出只通过单个模态试验获取车身静态刚度和动态刚度的方法,并对此进行了有限元分析验证;DELEENER等[8]详细阐述了利用基于子结构的频率响应函数(FRF based on substructuring,FBS)技术以及模态测试技术以获取白车身静态刚度的方法。但这些获取车身静刚度的方法较为繁琐,且耗时费力,在试验条件尚不完备的情况下,难以将其应用于工程实践。
为研究白车身弹性体模态与静刚度的内在联系,本文以线性系统的模态理论为基础,将简单矩形框架中模态与静刚度的关联性推广到白车身,并通过有限元仿真直接提取白车身的模态参数,再以此评估整体的静态刚度。然后将该方法获得的静刚度与传统静力学计算值作对比,以验证理论的正确性。此方法简单高效,在车身开发前期,不仅能在只计算模态的情况下获取白车身的静刚度,而且能定量地反映模态和静刚度两项性能的关联性,这为低阶模态和刚度性能的目标设定提供了重要依据。
1 基本理论
1.1 矩形框架的刚度
工程上,一般用一具体的数值来表达系统的刚度值。例如,汽车工业上就是用弯曲刚度和扭转刚度来表征白车身抵抗弯曲和扭转变形能力的量。白车身可以看作一个大型线性系统,其力学特性应与简单线性系统保持一致,因此可以通过研究简单矩形框架刚度与模态的关联性来反映车身系统的力学规律。
图1所示为矩形框架结构。在位置1、2、3、4约束方向x、y、z的平动自由度,并在左右两边的中点上分别施加垂直于矩形框架平面向下且大小为F的力。若记F5=F6=-F,那么根据静力平衡,很容易得到F1=F2=F3=F4=F/2。若将框架看作一个离散的线性系统,那么框架系统所受的外力可写成如下向量形式:
(1)
式中,VB为弯曲工况的外力系数向量。
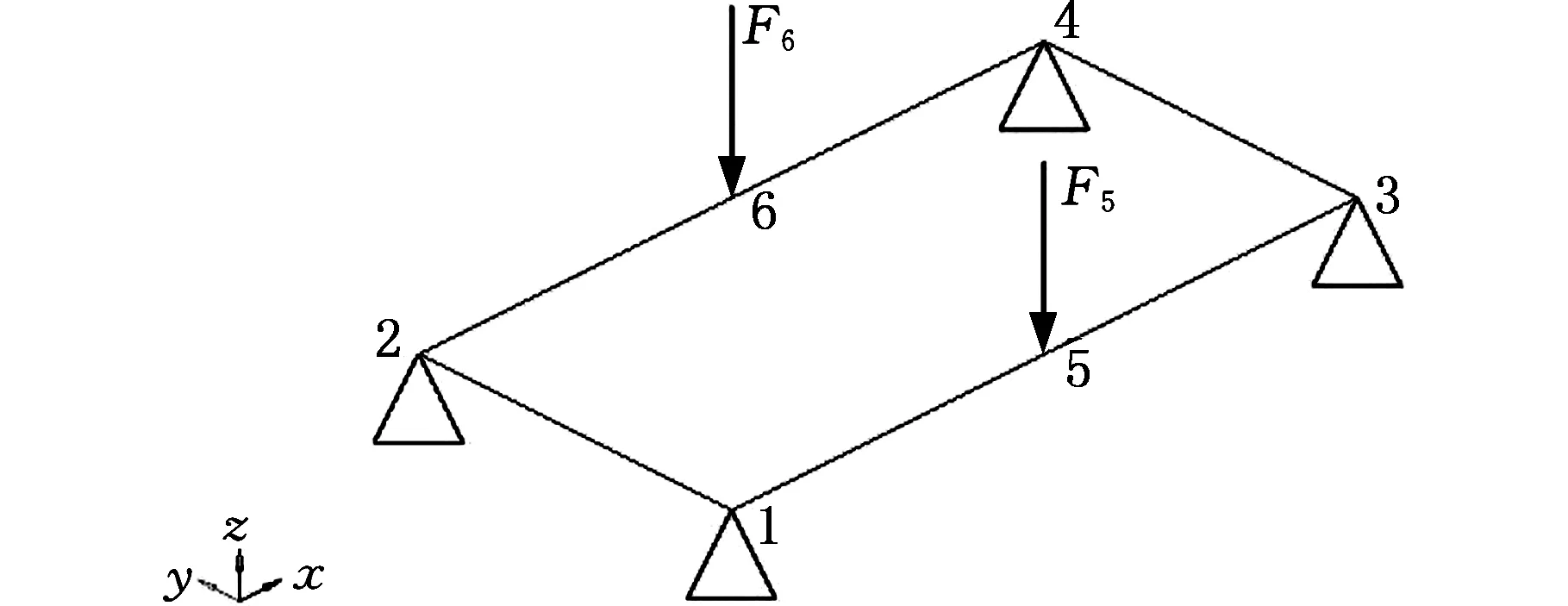
图1 矩形框架的弯曲Fig.1 Frame bending
弯曲刚度KB一般被定义为所施加的载荷与施力点在载荷方向(即垂直于矩形框架方向)偏移量的比值,即
或
(2)
式中,z1~z6分别为点1~点6的垂直方向的位移。
图2为矩形框架结构的扭转工况图。在位置1、2施加垂直于矩形平面方向且大小相等(均为F)、方向相反的两个力,并约束位置3、4、5处方向x、y、z的平动自由度,其中位置5为边L12的中点。若记F1=F,F2=-F,由静力平衡,可得到F3=-F,F4=F,在整个框架系统中,写成向量的形式为
P=(0,1,0,-1,0,-1,0,1,0)TF=VTF
(3)
式中,VT为扭转工况的外力系数向量。
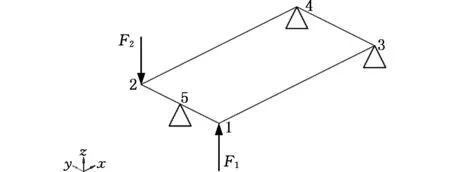
图2 矩形框架的扭转Fig.2 Frame torsion
根据扭转刚度的定义,矩形框架的扭转刚度为施加于L12端的扭矩比上L12与L34相对扭转角,即
或
(4)
式中,L12、L34分别为矩形框架前后边长。
1.2 模态与静刚度的关系
一般地,对于n自由度线性定常系统的无阻尼自由振动有
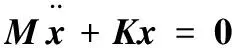
(5)
式中,M为系统的质量矩阵;K为系统的刚度矩阵;x为位移列向量。
对于复杂的线性系统,式(5)是相互耦合的微分方程组,通过一般方法很难求解甚至不能求解,因此可以令x=Φη。从而使式(5)解耦[9]。在等式两边乘ΦT,得到
(6)
式中,Φ为系统的模态矩阵;η为系统的模态坐标。
由于Φ的各阶模态向量(即各阶主振型)关于质量矩阵和刚度矩阵两两相互正交,因此Mm=ΦTMΦ为对角阵,主对角元素为各阶模态质量;Km=ΦTKΦ同样为对角阵,主对角元素为各阶模态刚度。对于第i阶模态,有

(7)
(8)
式中,ωi为第i阶角频率;fi为自然频率;Km,i为模态刚度;Mm,i为模态质量。
根据结构力学,线性系统的静力学方程为
Kx=P
(9)
式中,P为外力列向量。
为了将线性系统的静态性能与动态性能联系起来,将x=Φη代入式(9),并同时在等式两边左乘ΦT得到
ΦTKΦη=ΦTP
或
(10)
当矩形框架受到静态弯曲力的作用时,根据式(10),在第i阶模态下有
(11)
式中,φi为第i阶模态向量;χj为弯曲工况下第j个坐标的广义力系数。
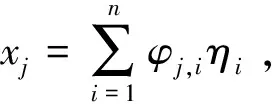
(12)
再将式(12)代入式(2)得到弯曲刚度KB与各阶模态参量的关系:
(13)
式中,1/KB为弯曲柔度。
同样地,在扭转工况下,对于第i阶模态有
(14)
式中,βj为扭转工况下第j个坐标的广义力系数。
(15)
将式(15)与式(4)联立,得到扭转刚度KT与各阶模态参量的关系式:
(16)
式中,1/KT为扭转柔度。
1.3 模态与静刚度的关联性理论在白车身上的应用
白车身类似于矩形框架结构,其相关参数应当满足式(13)和式(16),只是在推导过程中,应该注意,白车身静刚度试验的测点与加载、约束点的位置并不重合,因此在利用该方法计算静刚度时,需同时考虑试验加载、约束位置以及测点位置的模态变形量。那么,对于白车身,式(13)和式(16)分别改写为
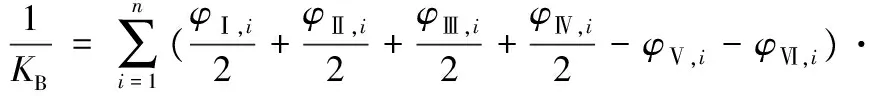
(17)
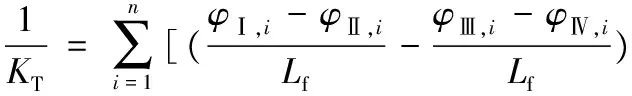
(18)
式中,φⅠ,i~φⅥ,i为加载或约束点处第i阶z向模态变形量;φ1,i~φ6,i为测点处第i阶z向模态变形量;Lf为前悬减振器中心之间的距离;L12与L34分别为前测点之间以及后测点之间的距离。
式(13)和式(16)右边各项即为白车身各阶模态的弯曲(扭转)柔度贡献量,其具体含义为白车身的静态柔度等于各阶模态柔度贡献量之和。通过这一等量关系,可将白车身模态性能与静刚度性能联系起来。
2 白车身静刚度计算
2.1 白车身有限元模型的建立
现将某款商用车的白车身在Hypermesh前处理软件中划分成691 735个节点、673 350个单元的离散结构,网格单元主要包含1D、2D、3D以及0D或rigids几种类型,其中2D壳单元占主要部分(约90.3%),主要用于模拟车身的钣金件结构。2D网格划分采取CQUAD4及CTRIA3的混合单元形式,网格尺寸为8~15 mm,并注意控制单元的质量。胶粘连接采用Adhesives单元进行模拟,钣金件之间的点焊采用Acm单元模拟,另外利用RBE2单元并保证节点对齐来模拟缝焊。车身主要材料为钢材,密度为7.85×103kg/m3,泊松比为0.3,弹性模量为210 GPa。图3所示为分析用到的白车身有限元模型。

图3 白车身有限元模型Fig.3 Finite element model of body in white
2.2 基于静力学有限元分析计算白车身静刚度
白车身弯曲试验中,一般在车身前、后减振器座处进行固定,再在前后悬架连线的中垂面上施加一对垂直向下的作用力,施力点位于纵梁中心正上方的地板上。根据试验具体情况,施加约束和载荷,建立弯曲工况的有限元模型,并提交计算。在计算弯曲刚度时,选取6个测点:分别为过前后减振器座中心铅垂面与前后纵梁底面中心的交点(测点1~4),以及加载点正下方的纵梁底面的中心处(测点5、6)。测量这6个测点的z向位移,分别记作z1~z6,根据式(2)可以得到车身的弯曲刚度为6 904 N/mm,弯曲柔度即为1.448×10-4mm/N。
在扭转试验中,一般先将车身的后减振器座或后悬架弹簧座进行固定,然后在左、右前减振器座施加一对垂直且反向的力,以形成力偶。根据试验具体情况,建立扭转工况的有限元模型并进行求解。测点选取与弯曲刚度的测点1~4一致,读取4个测点的z向位移,再根据式(4),可以求得扭转刚度为526 535N·m/rad,扭转柔度即为1.899×10-6rad/(N·m)。
2.3 基于模态理论计算白车身静刚度
为验证式(17)和式(18)所描述的静刚度计算方法,同样以该白车身模型为例,根据以上两式对弯曲刚度和扭转刚度进行计算。在计算之前,需要知道以下参数:①白车身的各阶模态频率与质量(或是模态刚度);②白车身在各处测点以及加载、约束点的模态变形量。以上数据都可以通过有限元仿真得到。
2.3.1白车身模态计算
弹性体模态作为白车身结构的固有属性,与车身承受的外部载荷无关,且白车身可以近似看作弱阻尼线性系统(阻尼比通常小于5%),因此在模态计算时,无需设置边界条件与阻尼系数,可直接利用MSC. Nastran中的Lanczos法进行求解,输出时选择各阶模态最大变形量归一化。提取各阶弹性体模态参数,其中前20阶模态系数的具体数值见表1。其余各阶不作逐一列举。
由表1可以看出该白车身有限元模型前20阶弹性体模态的频率、模态质量和模态刚度,这三者之间的关系满足式(8)。由式(17)与式(18)可知,模态变形量的测点共有12个,分别为静刚度试验时的6处加载或约束点以及6处测点。将加载、约束点记为数字Ⅰ~Ⅵ,与之对应的测点记为数字1~6,可以得到12个测点各阶z向模态变形量,也就是各阶模态振型在测点处的z向分量,见表2(这里只列出了前10阶)。
2.3.2基于模态理论计算白车身弯曲刚度
根据1.3节中提到的通过模态参数计算弯曲刚度的方法,将提取的模态数据(模态频率、模态质量与测点处的模态变形量)代入式(17)右边,可以得到各阶模态的弯曲柔度贡献量。表3所示为前100阶弯曲柔度贡献量的具体数值。由表3可以看出,弯曲柔度在低阶模态中分布较为集中,与静力学方法计算的弯曲柔度相比,第6、7、8、13、15以及40阶的柔度贡献量较大,其中第8阶(一阶弯曲模态)的柔度贡献量最大,占静力学计算值的26.94%。
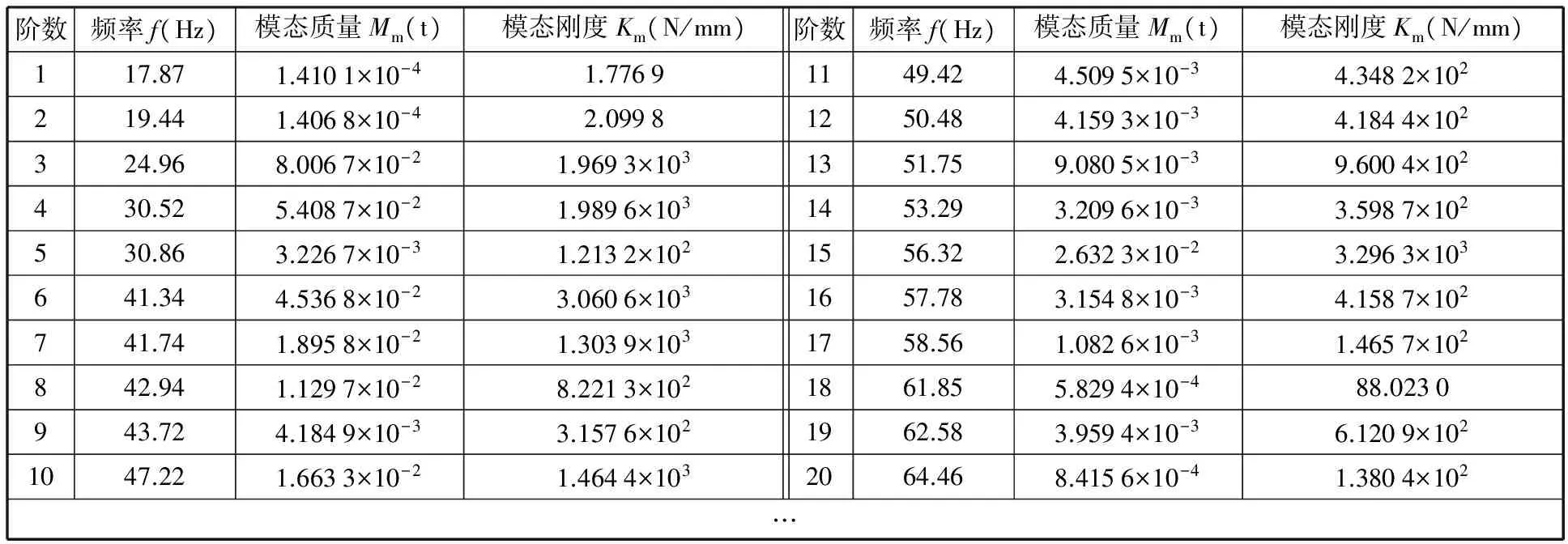
表1 前20阶模态参数Tab.1 Parameters of first 20 modes
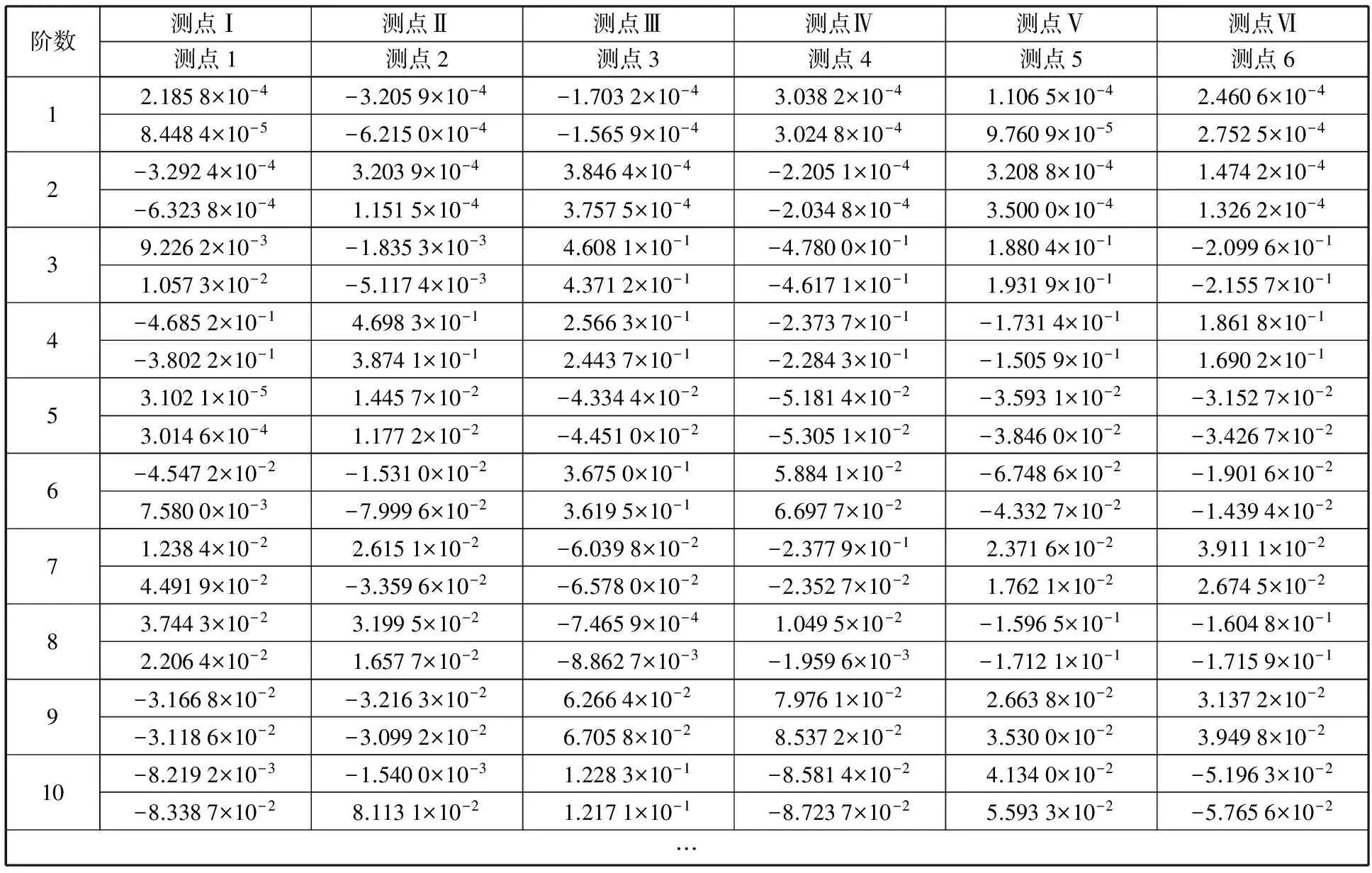
表2 12处测点的各阶模态变形量Tab.2 Modal deformations at 12 measure points
将各阶弯曲柔度贡献量累加,便可以得到白车身各阶弯曲柔度贡献量之和。由于白车身有限元模型总自由度数十分庞大,很难对其各阶模态柔度贡献量逐一求解,因此本文只计算了前10阶、前20阶、……、前100阶的柔度贡献量之和,具体数值如表4所示。由表4可以看到,在计算前10阶时,弯曲柔度贡献量之和与2.2节中的弯曲柔度值相差-63.46%,与前20阶相差-36.59%,至前50阶,差距减小到-8.89%,且随着计算阶数的增加,其数值仍然在不断接近静态弯曲柔度值,考虑前100阶时,弯曲柔度贡献量之和与静态弯曲柔度的差距已经减小到-4.80%。
由表4可以看出,随着计算的阶数增加,所得的柔度值越来越逼近某一个固定的数值,这与前面静力学计算方法获得的弯曲柔度十分类似。其中前50阶收敛速度较快,而50阶之后的收敛速度明显下降,且柔度变化趋于平缓,这表明白车身弯曲柔度在各阶模态的分布并不是均匀的,而是集中在较低阶的模态,在一些低阶弯曲模态(特别是一阶弯曲模态)中,这一现象尤为明显。由此可以得出结论,白车身的静态弯曲柔度等于各阶弯曲柔度贡献量之和,且低阶弯曲模态与弯曲刚度之间存在着非常紧密的联系。在实际应用中,考虑到前50阶弯曲柔度贡献量之和已经非常接近静力学计算值了,所以可将前50阶贡献量之和基本作
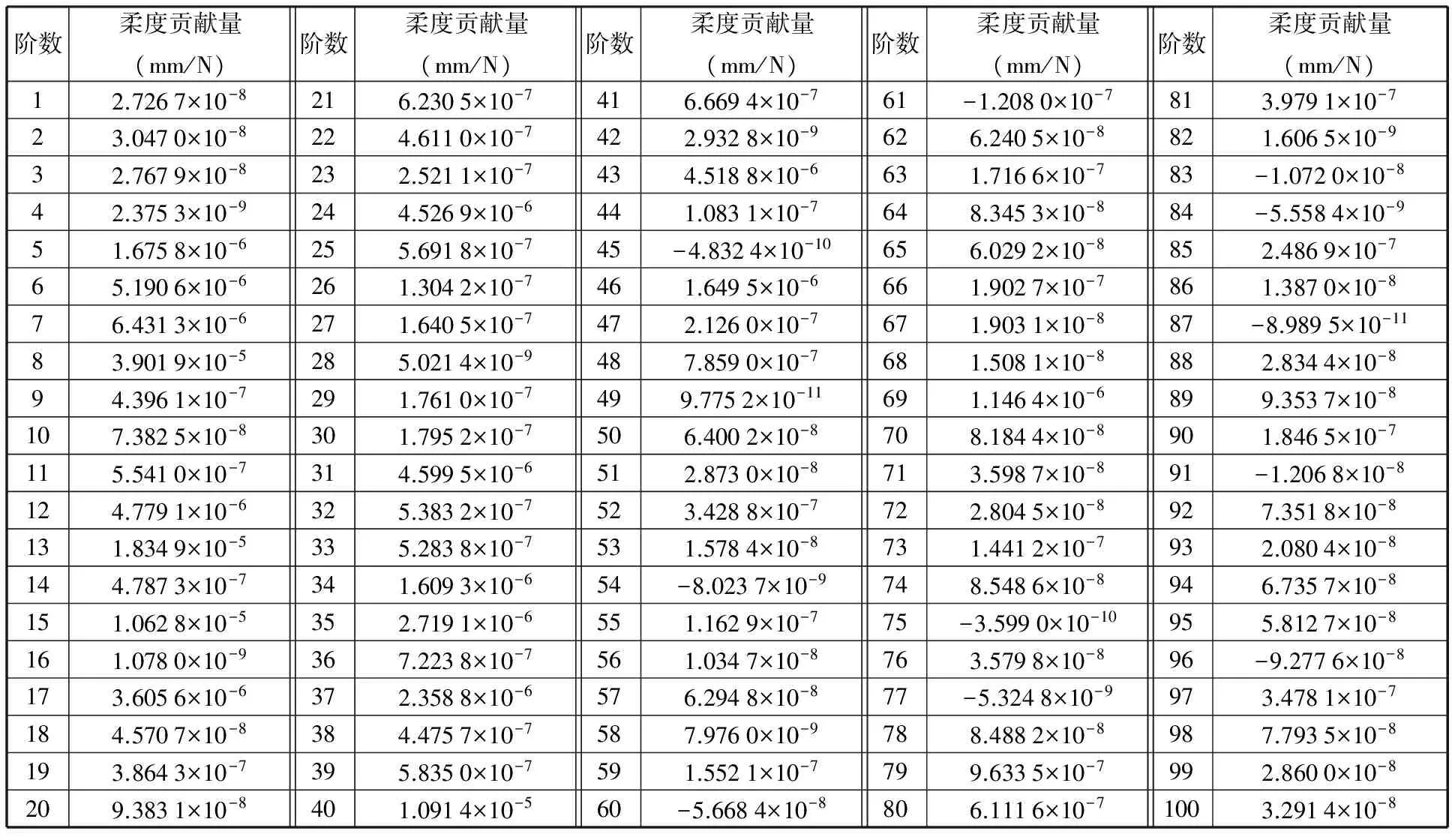
表3 各阶弯曲柔度贡献量Tab.3 Modal contributions to bending compliance

表4 弯曲柔度贡献量之和与静态弯曲柔度的对比Tab.4 Comparison between the sum of modalcontributions to bending compliance and staticbending compliance
为车身整体的弯曲柔度。所获得的弯曲柔度约为1.320×10-4mm/N,弯曲刚度为7 578 N/mm,与静力学方法获取的刚度值相比,增大了9.76%,这说明式(17)所描述的计算方法具有较高的精度,故在车身开发前期,可利用这一方法同时获得白车身的模态与弯曲刚度。另外,由于低价弯曲模态与弯曲刚度存在定量关系,因此在确定合适的低阶弯曲模态频率后,可由此大致设定弯曲刚度的目标值,这样不仅能避免由于刚度目标值设定过高而造成材料浪费,并且对汽车轻量化有着重要意义。反之在确定弯曲刚度满足性能需求之后,也可根据这一关系合理地规划低阶弯曲模态的目标值。
2.3.3基于模态理论计算白车身扭转刚度
利用模态理论计算扭转刚度的方法与计算弯曲刚度的方法类似,将各阶模态频率、模态质量(或模态刚度)与测点的z向模态变形量代入式(18)右边,获得各阶模态扭转柔度贡献量,具体数值见表5。由表5可以看出,相比弯曲柔度分布的情况,扭转柔度在低阶模态的分布更为集中,第3阶(白车身背门框扭动)和第4阶(一阶扭转模态)占据静力学计算值的75.06%,其中第4阶的柔度贡献量最大,占总数的53.79%。
根据表5中的数据求得前10阶到前100阶的柔度贡献量之和,其具体数值见表6。与2.2节中的静力学计算值作比较,结果发现,前10阶的扭转柔度贡献量之和已经与静力学计算值非常接近(达到其80.47%),根据前面的分析,这主要是因为一阶扭转模态的贡献比非常大,占到静态扭转柔度值的一半以上。随后计算的前20阶到前50阶的扭转柔度贡献量之和依然在不断接近静态扭转柔度,计算前20阶时,与静力学计算值相差-14.79%,到前50阶时,差值已经减小到-5.54%。由表6可知,随着计算阶数增加,扭转柔度贡献量之和逐渐逼近一固定值,这个值与前面计算的车身扭转柔度非常接近。前10阶曲线增长的速度非常之快,前20阶到前50阶速度有所放缓,且前50阶之后,扭转柔度曲线变化趋于平缓。这一现象同样说明,扭转柔度在各阶模态的分布也不是均匀的,而且集中情况相较于弯曲柔度更加明显,低阶模态对于扭转柔度贡献更大,尤其是一阶扭转模态对于扭转柔度的贡献更为突出。由于前50阶的扭转柔度贡献量已经与静力学计算值非常接近,因此车身整体的扭转柔度也可基本用前50阶模态柔度贡献量之和表示。用模态方法计算得到的扭转柔度为1.794×10-6rad/(N·m),与之对应的扭转刚度的值近似为557 392 N·m/rad,相比静力学计算值只增大了5.86%。结果表明,基于式(18)对扭转刚度进行有限元计算是可行的,且具有很高的精度,在车身开发前期,可利用这一方法同时获得白车身的模态与扭转刚度。另外,根据低阶扭转模态与扭转刚度之间的定量关系,可在确定合适的低阶扭转模态频率之后,大致设定扭转刚度的目标值,这能很好地避免由于刚度过剩而引起的材料浪费。同样地,在确定扭转刚度满足性能需求之后,也可根据这一关系合理地规划低阶扭转模态的目标值。

表5 各阶扭转柔度贡献量
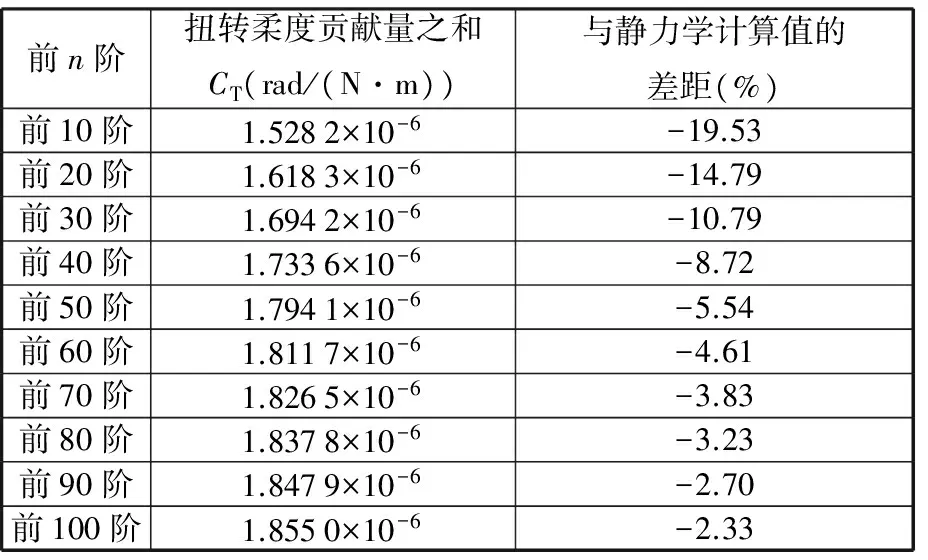
表6 扭转柔度贡献量之和与静态扭转柔度的对比Tab.6 Comparison between the sum of modalcontributions to torsional compliance andstatic torsional compliance
3 白车身静刚度试验
为了检测有限元分析结果的准确性与可靠性,故对该车型的白车身实施静刚度台架试验。试验的的仪器主要由两部分组成:弯曲(图4)刚度试验台、扭转刚度试验台(图5)以及车身数据采集系统。试验时的约束与加载情况如2.2节所述,测点布置在前、后纵梁以及门槛梁底面,呈左右两边对称布置,每边各13个测点,其中纵梁底面为8个,门槛梁底面为5个,弯曲试验和扭转试验均采取逐级加载方式,分别读取不同载荷下测点的z向位移,然后将每个测点在不同载荷下的位移取加权平均值,并由此绘制梁的变形曲线图。通过静刚度计算方法,便可得到白车身的弯曲刚度和扭转刚度。

图4 弯曲试验Fig.4 Bending test

图5 扭转试验Fig.5 Torsion test
表7所示为白车身静刚度的有限元分析值与此次试验值的对比。由表7可以看出,样车的弯曲刚度为7 026 N/mm,相比之下,通过有限元分析获得的弯曲刚度值误差分别只有-1.74%(静力学方法)和7.86%(模态方法)。该样车的扭转刚度为543 750 N·m/rad;与之相比,通过有限元计算得到的扭转刚度值的误差分别为-3.17%(静力学方法)和2.51%(模态方法)。弯曲刚度和扭转刚度的仿真误差均在±8%以内,因此可认为此次有限元分析是可靠的。
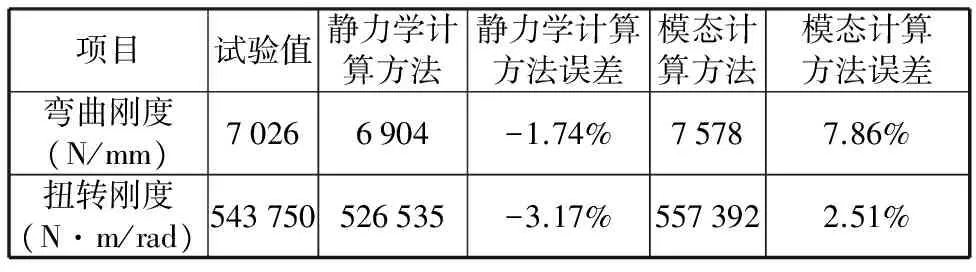
表7 有限元分析值与试验值的对比
4 结论
(1)与简单的线性系统相似,白车身的弯曲柔度与扭转柔度均等于各阶模态柔度贡献量之和,计算时使用的阶数越多,结果越精确。但通常情况下,只考虑前50阶模态参数,与静力学计算方法比较,其计算误差可控制在10%以内。
(2)根据低阶模态与静刚度的定量关系,可在车身开发前期合理设定模态与静刚度性能的目标值,同时也可在车身结构的设计与优化中起到重要作用。
(3)静态弯曲柔度与静态扭转柔度在各阶的分布规律存在差异,弯曲柔度分布较为离散,而扭转柔度分布较为集中。
(4)低阶弯曲(扭转)模态与弯曲(扭转)刚度联系紧密,通常一阶弯曲模态、扭转模态所对应的弯曲柔度、扭转柔度贡献比最大,在车身开发前期,对于难以识别的模态振型,这一规律可作为低阶模态识别的重要依据。
参考文献:
[1] 高云凯, 张婷婷, 刘海立. 轻型客车车身结构评价方法及应用[J]. 中国机械工程,2012, 23(17):2116-2121.
GAO Yunkai, ZHANG Tingting, LIU Haili. Evaluation Method for Structural Performance of Light Bus Body and Its Applications[J]. China Mechanical Engineering,2012,23(17):2116-2121.
[2] GRIFFITHS D, AUBERT A, GREEN E R, et al. A Technique for Relating Vehicle Structural Modes to Stiffness as Determined in Static Determinate Tests[J]. SAE Technical Paper Series,2003-01-1716.
[3] PASHA H G, ALLEMANG R J, PHILLIPS A W, et al. Estimation of Bending Compliance (Stiffness) from Free-Free FRF Measurements: eBCF Theory[M]// Experimental Techniques, Rotating Machinery, and Acoustics, Volume 8. New York: Springer International Publishing,2015:141-155.
[4] PASHA H G, ALLEMANG R J, PHILLIPS A W, et al. Estimation of Torsional Compliance (Stiffness) from Free-Free FRF Measurements: eRCF Theory[M]// Experimental Techniques, Rotating Machinery, and Acoustics, Volume 8. New York: Springer International Publishing,2015:121-132.
[5] PASHA H G, ALLEMANG R J, BROWN D L, et al. Static Torsional Stiffness from Dynamic Measurements Using Impedance Modeling Technique[M]// Dynamics of Coupled Structures, Volume 1. New York: Springer International Publishing,2014:307-316.
[6] WAHYUNI E, JI T. Relationship between Static Stiffness and Modal Stiffness of Structures[J]. Iptek the Journal for Technology & Science,2010,21(2):1-5.
[7] HELSEN J, CREMERS L, MAS P, et al. Global Static and Dynamic Car Body Stiffness Based on a Single Experimental Modal Analysis Test[C]//Proceedings of ISMA2010 Including USD2010. Belgium,2010:2504-2521.
[8] DELEENER J, MAS P, CREMERS L, et al. Extraction of Static Car Body Stiffness from Dynamic Measurements[J]. SAE Technical Paper,2010-01-0228.
[9] 倪振华. 振动力学[M]. 西安:西安交通大学出版社,1989:161-227.
NI Zhenhua. Mechanics of Vibration[M]. Xi’an: Xi’an Jiaotong University Press,1989:161-227.

