基于不可分小波变换与Zernike矩的印刷体汉字识别方法
刘 斌 肖惠勇
(湖北大学计算机与信息工程学院 湖北 武汉 430062)
0 引 言
汉字识别是一种使用计算机运行用户的预设算法来提取汉字的特征,并与机器内预存特征进行匹配识别,将汉字图形自动转换成某种代码的一种技术[1]。目前汉字识别可分为手写体识别和印刷体识别两种。本文主要对单体印刷体汉字识别进行研究。目前,主要通过预处理、特征提取以及识别这三步对印刷体汉字进行识别。预处理一般包含对汉字图片的除噪、倾斜校正、切分、二值化、归一化等一系列操作[1],其目的是为后一步的特征提取提供质量更好的汉字图像,使得提取的特征更准确一些。第二步汉字的特征提取是最重要也是研究最多的一部分,所提取的汉字特征的好坏以及准确性将直接决定最后一步的汉字识别率的高低。识别这一步将使用机器学习中的分类法,聚类法或者是神经网络的方法(如:BP神经网络)利用上一步得到的汉字特征对汉字进行识别。对于上述的三个步骤,本文主要关注与研究的是第二步的汉字特征提取。
与其他字符集不同,汉字种类非常多,我国常用汉字约为2 500个;相似字也多,如“戊”、“戍”、“戌”、“已”、“己”、“巳”等。因此,要求识别算法能够如肉眼般区分这些相似字间的细微差异,否则将识别错误。为了克服这些困难,研究者们提出了大量的基于统计的和基于结构的特征提取方法:根据汉字笔划的复杂程度,用汉字的黑像素数量占整个汉字图像像素数量的比值作为特征进行描述的汉字繁简度特征提取算法[1]。汉字的构造特点决定汉字周围含有较多的信息,提取这些区域的特征作为分类依据,从而有了汉字网格特征[2]。汉字不变编码特征[3]的出发点在于印刷汉字特有的规律:横平竖直。以汉字图像中被表示笔划的黑像素所包围形成的封闭背景区域作为特征——汉字结构及封闭区域特征提取算[1]。在理想情况下,用这些方法提取的特征来识别汉字会有较高的识别率。但当汉字大小,方向改变,或是出现噪声污染时,这些方法的识别率将会大打折扣。1962年, Hu[4]从几何不变量理论中找到灵感,提出几何矩概念,并推导得出了几何不变矩的旋转、平移及尺度不变性。于是,研究者们将矩这一概念应用到了模式识别中。然而,Hu 矩虽然具有不变性,但其来自非正交函数族,因此冗余信息较多,并且随着矩阶数的变大其计算量会快速增长,无法用于实际应用。随后研究者们又找到了大量基于正交基的正交矩方法,其中的Zernike正交矩[5]就拥有很好的性能。Zernike正交矩本身是具有旋转不变性的,再对其进行数学变换,可使其同时拥有平移和尺度不变性。1990年,Khotanzad等[5]验证了Zernike矩的上述特性,并对英文字母的识别进行了实验,发现将图像的Zernike矩作为特征识别时可以得到较高的识别率,有噪声情况下识别率达到92%。由此可见,Zernike矩是成功的,但它的缺点也是明显的:计算量大,同时阶数越高,Zernike矩对噪声就越敏感,造成的错误识别就越多。
另一方面,通过对小波变换的学习,发现最新的不可分小波变换拥有更好的特性。首先,不可分小波是各向同性的[6-8],对图像做不可分小波变换可以捕获图像在各方向上的奇异性,从而得到近乎完整地图像边缘。这一特性可以保证对汉字图像做不可分小波变换后得到的图像可以保存正确的汉字轮廓特征,提高汉字识别率。其次,对一幅图像进行不可分小波变换后得到的低频图像是原图像的1/4大小[6],后续对图像进行Zernike矩特征提取时计算量也将降低为原来的1/4。最后,不可分小波四通道分解可将原图像分解为一幅低频子图和三幅不同方向的高频子图[6-7],这将很好地把原图像的低频信息与高频信息分离开来。而图像的噪声正是属于高频部分的,所以分解得到的低频子图将几乎不含噪声,达到深度除噪的目的,从而提高汉字的识别率。
针对前文所说的Zernike矩方法的不足,同时结合上述最新的不可分小波变换的优点,提出了结合不可分小波四通道分解方法与Zernike矩方法的特征提取方法。先对汉字图像做合适的不可分小波分解得到所需的低频子图,然后计算该低频子图的前6阶Zernike矩,得到能准确代表汉字图像的Zernike矩特征,将这6阶的Zernike矩特征联合起来作为最后用于汉字识别的汉字特征。
1 二维小波分解
1.1 二维小波变换
设x=(x1,x2)T∈R2,φ(x)∈L2(R2)为二维小波函数,A是2×2的伸缩矩阵,b是平移向量,b=(b1,b2)T,则令:
(1)
设数f(x1,x2)∈L2(R2),则二维小波变换的定义[6-7,15]为:
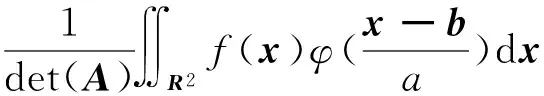
(2)
式中:a=det(A),式(2)是二维小波变换的数学简记形式,φA,b(x)表示φ(x)二维位移和尺度伸缩。
1.2 二维不可分小波变换
二维小波变换有可分和不可分小波变换这两种[7-8]。二维可分小波变换是直接由一维小波基的张量积得到的,而不可分小波则是直接在二维空间上进行构造的,得到了一些新的特性。如:在保证紧支撑正交性时,还具有对称性,保证图像相位不失真;同时,它还具有各向同性的特性,以捕获所有方向上的奇异性。
Daubechies[7,9]已经证明小波分解可以用信号或图像和离散滤波器的卷积来实现。因此需要知道的是如何构造小波的低通和高通滤波器。
Chen等[10]以MRA为基础,使用矩阵扩充法,得到了一种可以构造高维不可分小波滤波器组的一般方法,此方法最大的优点是可以更加自然地让滤波函数过渡到小波函数。以此为基础,下面给出目前二维不可分小波滤波器组的构造方法。

(3)



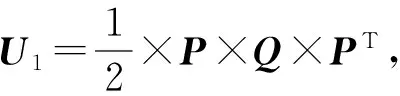
显然,它们是一组不可分小波滤波器,具有对称性(关于滤波器中心对称或反对称)、紧支撑,可以验证,它具有正交性,是一组完全重构滤波器。
2 Zernike矩
1980年Teague提出了Zernike矩[5,11-12,16],图像f(x,y)的m重,n阶Zernike矩的定义为Zmn:
(4)

(5)
当Zernike矩用于图像识别时,设图像旋转后变为f′(r,θ)=f(r,θ-α),则此时图像的Zernike矩:
(6)
从式(6)可知,旋转后Zernike矩只有相位变了,模值没变,具有旋转不变性[17]。
3 印刷体汉字识别实验过程
因为本文的研究主要针对特征提取这一步,所以预处理与识别这两步并未做过多的研究。实验中采用常用的预处理方法(除噪、二值化、平滑以及归一化等)和经典的BP神经网络识别法。即本文方法与单一的Zernike矩方法的实验步骤大致分为:原图像→预处理→提取特征以及BP神经网络识别这四部分。卷积神经网络识别法是将特征提取与识别结合在一起的,其实验过程为:原图像→预处理→LeNet-5神经网络识别这三部分。其中图像获取与预处理这两部分,三种方法是相同的,用来保证可对比性。实验是在MATLAB R2014a上进行的。
3.1 卷积神经网络
卷积神经网络概念的提出比较晚,但它却是一种高效的识别方法。由Hubel和Wiesel提出卷积神经网络(CNN)这一概念[18],经过长时间发展与完善,如今,具有高效性与高识别率特性的卷积神经网络已展现出巨大价值,成为了模式识别领域重要一员。一般认为卷积神经网络由4层构成,即:输入层、输出层、卷积层以及子采样层。卷积层对图像数据进行卷积计算,加入偏置向量,得到初步的特征映射,其计算公式为[19]:
(7)
表示从l层到l+1层要产生的特征数量,K表示卷积核(LeNet-5中,K为5×5矩阵),Mj为输入特征图的一个选择,b表示偏置向量。
计算出多个特征映射后,对它们进行加权求和,得到的值输入到子采样层,进而得到新的特征映射。多次重复该工作,最后再经过卷积核激活,将最终的特征输入到分类器中得到识别结果。LeNet-5[20]的结构图如图1所示。

图1 LeNet-5卷积神经网络结构图
3.2 图像获取
本文从《现代汉语常用字表》中随机抽取100种汉字用于实验。将这100种汉字随机分为10组,每组10种汉字进行汉字识别。每组中对每种汉字获取形态大小各不相同的100幅图片,其中90幅作为训练样本,10幅作为预测样本。另外,本文还从《现代汉语常用字表》中抽取了十几组形近汉字和车牌汉字进行对比实验,每三种汉字一组,每种汉字90幅图片,45幅作为训练样本,30幅作为预测样本,如:印刷体形近汉字:‘巳、已、己’,‘土、王、玉’,‘戊、戌、戍’,‘大、太、天’等,车牌汉字:‘鄂、桂、津’,‘闽、琼、苏’与‘湘、藏、浙’等。
图片集的构造是通过改变汉字大小来获取同一汉字不同大小的图像样本。如图2-图4所示,以‘己、已、巳’这一组为例。

图2 ‘己’字图像

图3 ‘已’字图像

图4 ‘巳’字图像
3.3 预处理
使用汉字识别预处理的方法[13]对图2-图4进行预处理(其他汉字也是进行同样的预处理),得到了单个汉字的图像,如图5所示。然后使用双线性插值法将所有图片归一化为统一大小的图像,如图6所示。进行大小归一化后,对图像进行细化处理,文字将变为骨架图形,笔画宽度为1 bit,如图7所示,消除了笔画粗细对汉字特征的影响。

图5 切分出来的单个汉字图片

图6 大小归一化为32×32后的‘己’、‘巳’、‘已’汉字图像

图7 细化后的‘己’、‘巳’、‘已’汉字图像
3.4 特征提取
特征提取这一步是为了得到能准确代表汉字的一些特征值。与单一Zernike矩法提取原图像特征不同,本文提出的方法是将不可分小波分解与Zernike矩相结合的特征提取方法:在对预处理后的文字图像进行不可分小波分解后,只取其中的低频子图作为样本图像,再计算样本图像的Zernike矩,得到汉字图像特征。
3.5 BP神经网络
本文实验的第四步采用BP神经网络。其基本原理是:输入信号Xi通过隐藏层节点,经过人工神经元的非线形变换,最终在输出节点产生输出信号Yk。分为训练与识别两步,训练的输入不仅有原向量X,还有前次实际输出量t与理想输出值Y的偏差。通过极小化误差的方式调整输入节点与隐藏层节点以及隐藏层节点与输出节点之间的联接权值Wij,反复训练后,使误差下降到精度范围内,训练停止,得到最终的权值和阈值。此时只需将要识别的样本输入训练后的网络即可得到最终识别结果。如图8、图9所示。
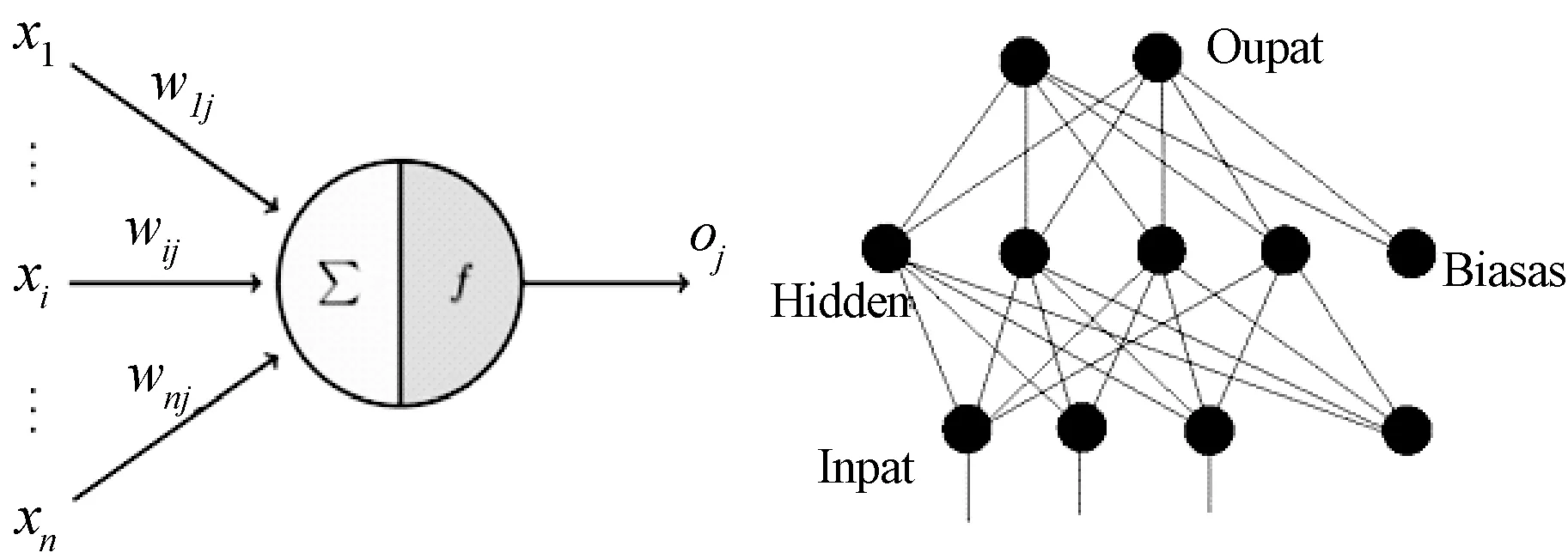
图8 单个人工神经元 图9 基本BP神经网络模型
3.6 具体实验步骤
按上述3.2节与3.3节方法取得的实验样本基本上是不含噪声的,按照3.2节所描述的两种实验方式进行训练和预测样本的选取。将原本的单一Zernike矩特征方法和卷积神经网络识别法作为本实验的对比实验:1)直接计算所选图像的Zernike矩,使用训练样本的Zernike矩进行训练学习,将预测(识别)样本的Zernike矩放入BP神经网络中进行网络识别,从而得到使用单一Zernike矩特征方法的识别率;2)将同样的训练样本放入卷积神经网络中进行训练学习,然后对同样的预测(识别)样本进行卷积神经网络识别,得到识别率。流程如图10所示。

图10 本文方法实验的流程图
本文方法的实验步骤如下:
(1) 使用本文提出的方法,先使用1.2节给出的滤波器组对样本图像做不可分小波分解,取其中的低频子图作为样本,从而得到新的样本图像集;
(2) 按照式(4)计算样本图像集的Zernike矩,将其中的训练样本集的Zernike矩放入BP神经网络中进行网络训练;
(3) 训练完成后,将预测(识别)样本集的Zernike矩放入BP神经网络中进行网络识别,从而得到对应的识别率。
4 实验结果与分析
实际应用中,因环境以及机器影响,印刷体汉字会带有一定的噪声。模拟噪声[5]:本文给原样本图像加上了椒盐噪声,概率分别为0.03、0.05和0.08,以‘已’字为例,见图11,做了三次带噪声的实验。此时因带有噪声,所以预处理时,先使用3×3的中值滤波器做一次简单的中值滤波后(为保护汉字图像细节信息,不使用均值滤波),见图12,再对滤波后的样本图像进行细化处理,见图13。细化处理完之后,得到的就是实验所需要的样本图像。

图11 分别加概率为0.03,0.05和0.08的椒盐噪声的‘已’字

图12 对图11进行中值滤波的结果
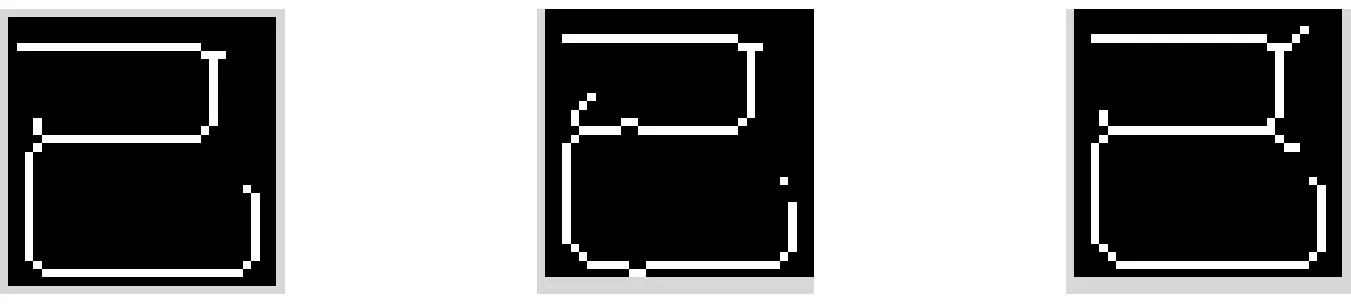
图13 对图12进行细化后的结果
本文还给原样本图像加上了高斯噪声(对应的均值为0,方差分别为0.01、0.05和0.1,见图14)。共做了三次带噪声的实验(此处直接将加高斯噪声的图像作为实验所需要的样本图像,因高斯噪声需用均值滤波器滤波,而均值滤波会模糊图像,造成高频信息的严重损失,所以此时并不进行滤波处理,又因为没有滤波,图像带有大量噪声,所以细化处理效果非常差,因此,不做细化处理)。

图14 分别加均值为0,方差为0.01、0.05、0.1的高斯噪声的‘已’字
4.1 实验结果
本文进行了大量的识别实验,并与单纯的使用Zernike矩提取原图像特征的方法[17]以及卷积神经网络识别法[19]进行了对比。下面是模拟实验的结果,不含噪声与模拟含噪声(加入高斯与椒盐噪声)。
4.1.1 十种字一组的实验
这次实验是识别随机选出的100种汉字,分为10组,每组10种汉字,每种汉字90幅训练样本,10幅预测样本。此实验中:BP神经网络部分使用的误差精度为0.02,学习率为0.01,训练次数为10 000,每组预测30次,取平均值;卷积神经网络识别法,网络结构为6c-2s-12c-2s,学习效率为1,批训练样本数为100,迭代次数1,2,…,30,取最好情况。
1) 无噪声与含椒盐噪声情况,见表1。
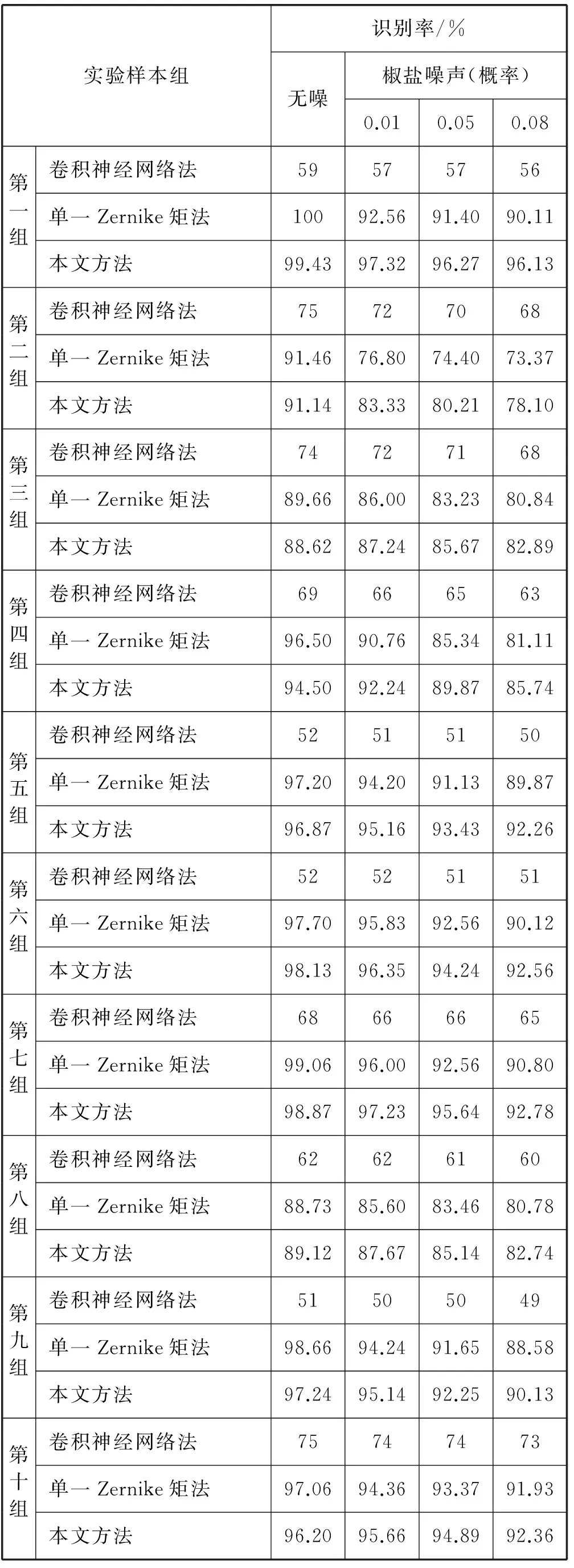
表1 无噪声与含椒盐噪声的识别率
2) 含高斯噪声情况,见表2。
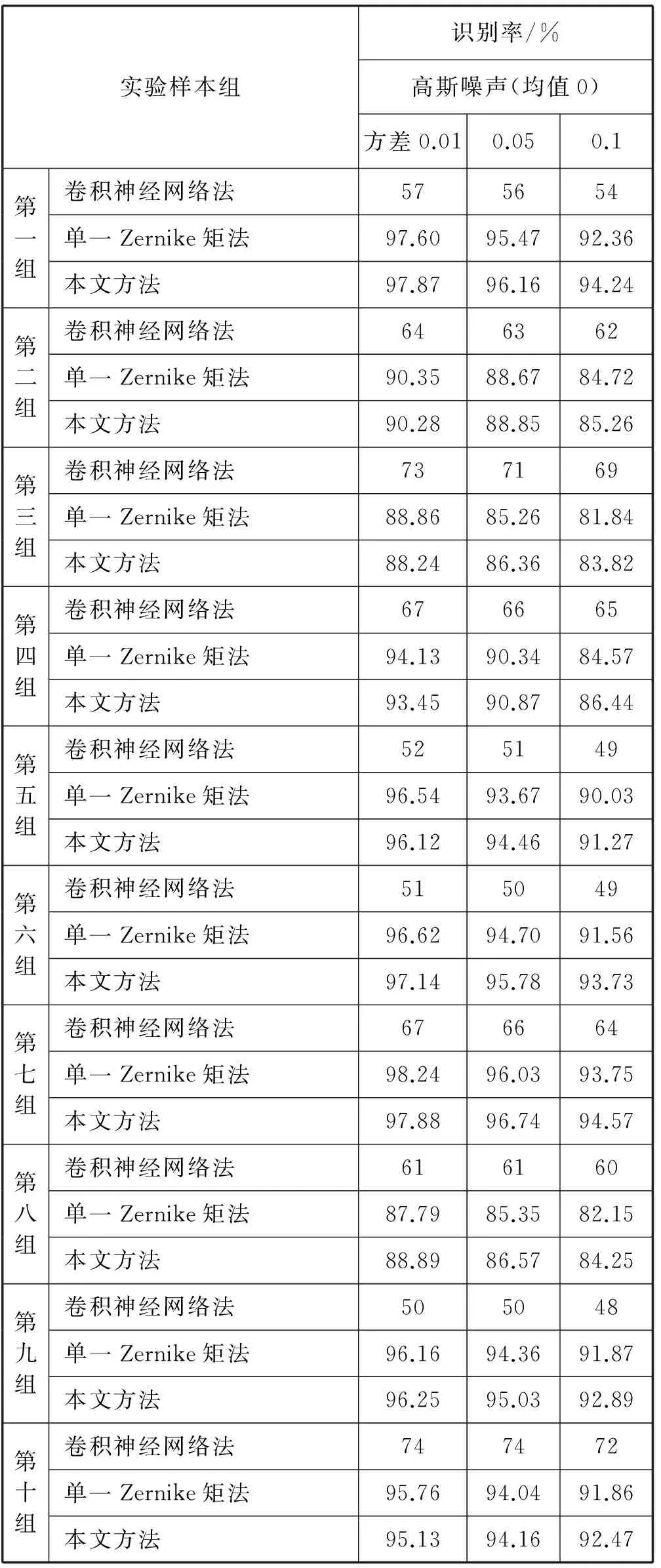
表2 含高斯噪声的识别率
4.1.2 三种字一组的实验
这次实验将每三种字组为一组,每种汉字45幅训练样本,30幅预测样本。此实验中:BP神经网络部分使用的误差精度为0.01,学习率为0.005,训练次数为10 000,每组预测30次;卷积神经网络识别法,网络结构为6c-2s-12c-2s,学习效率为1,批训练样本数为27,迭代次数1,2,…,30。
1) 不含噪声情况
当实验样本不含噪声时实验结果如表3所示。

表3 未加噪声时的识别率
2) 含椒盐噪声情况
概率为0.03的椒盐噪声实验结果如表4所示。
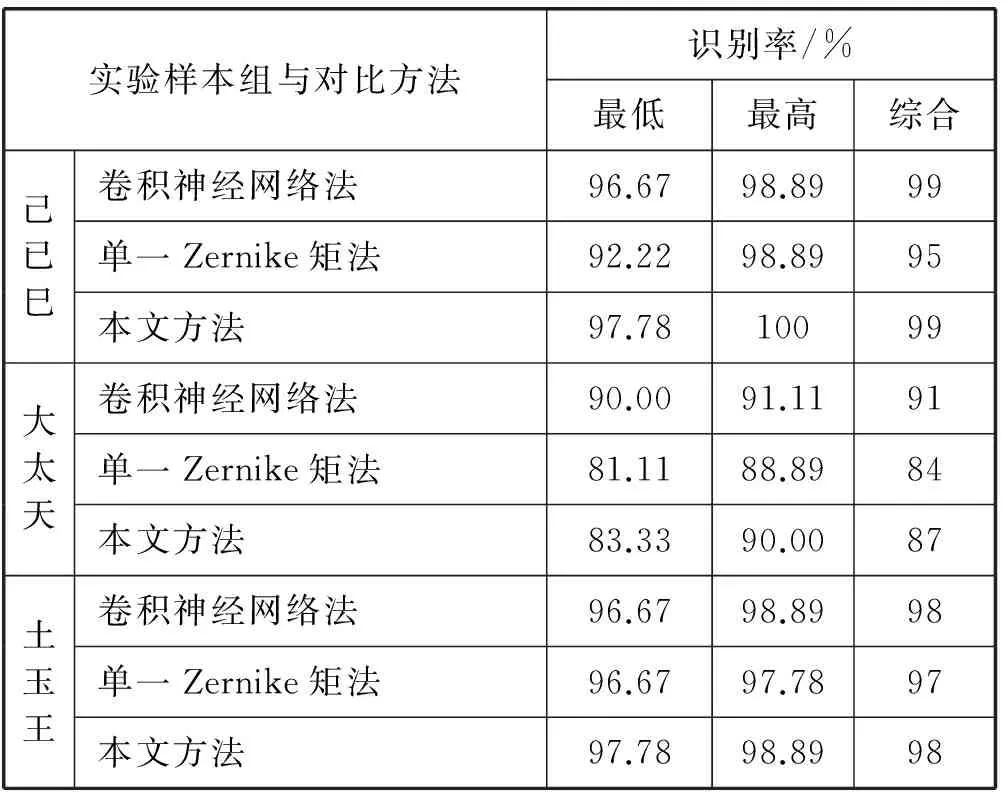
表4 椒盐噪声概率为0.03的识别率
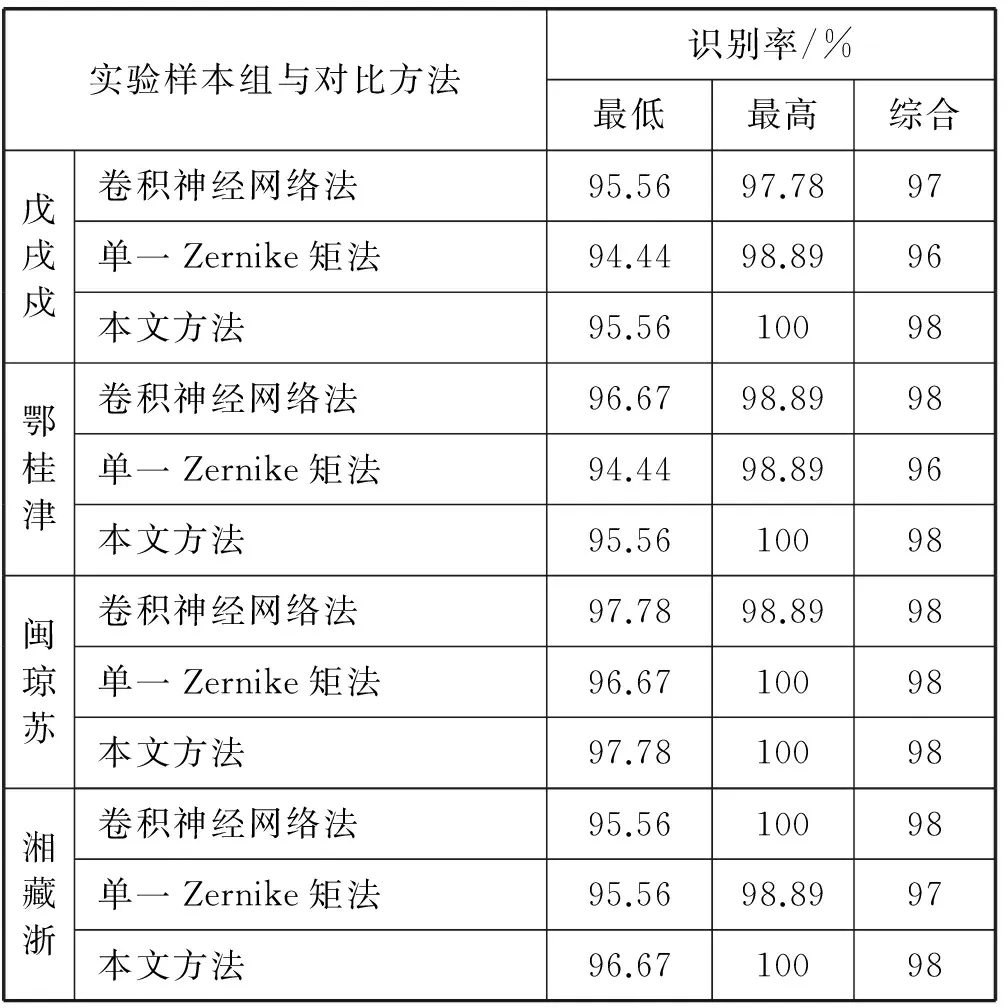
续表4
概率为0.05的椒盐噪声实验结果如表5所示。
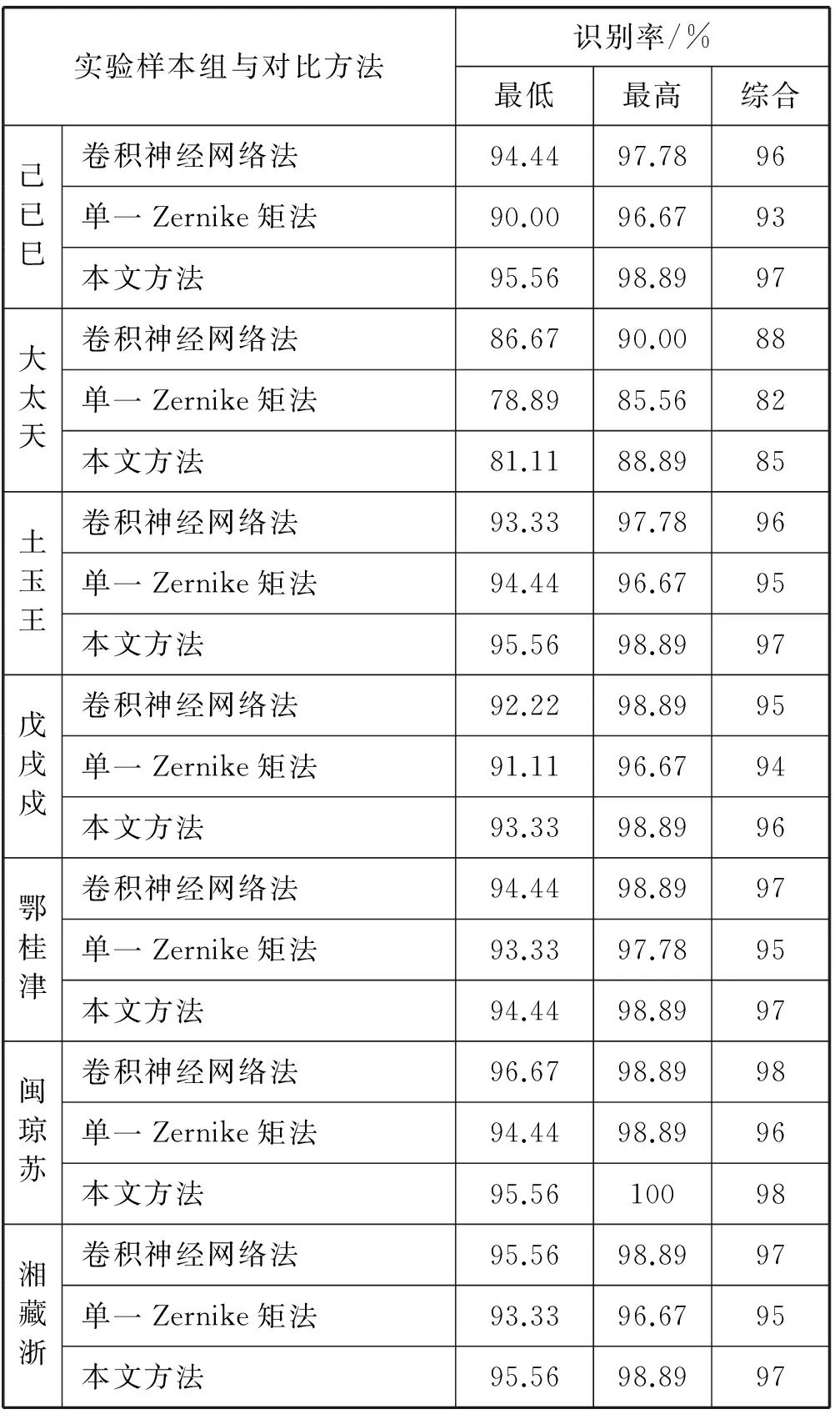
表5 椒盐噪声概率为0.05的识别率
概率为0.08的椒盐噪声实验结果如表6所示。

表6 椒盐噪声概率为0.08的识别率
3) 含高斯噪声情况
高斯噪声的方差为0.01的实验结果见表7。

表7 均值为0,方差为0.01的高斯噪声的识别率

续表7
高斯噪声的方差为0.05的实验结果见表8。
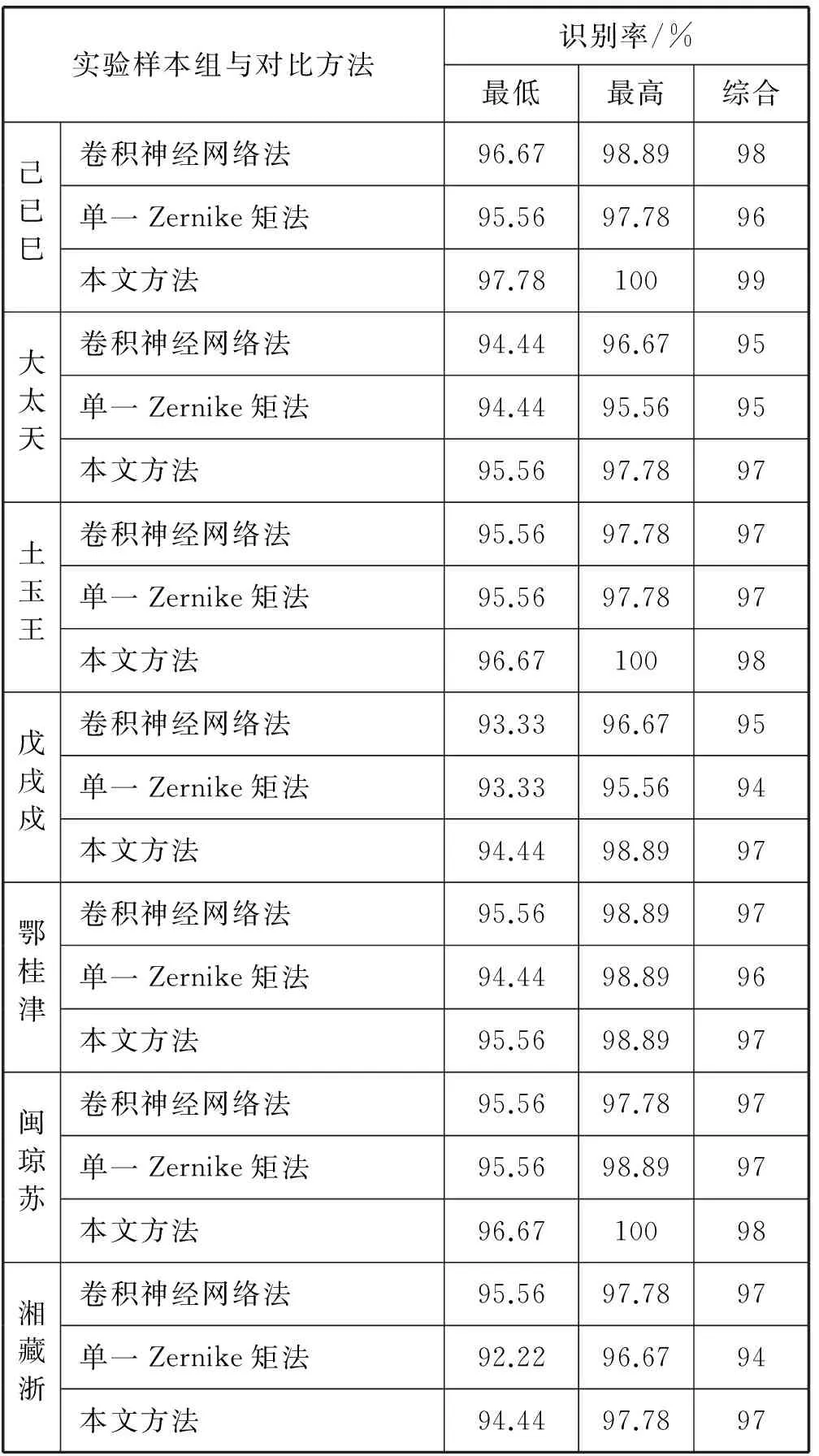
表8 均值为0,方差为0.05的高斯噪声的识别率
高斯噪声的方差为0.1的实验结果见表9。
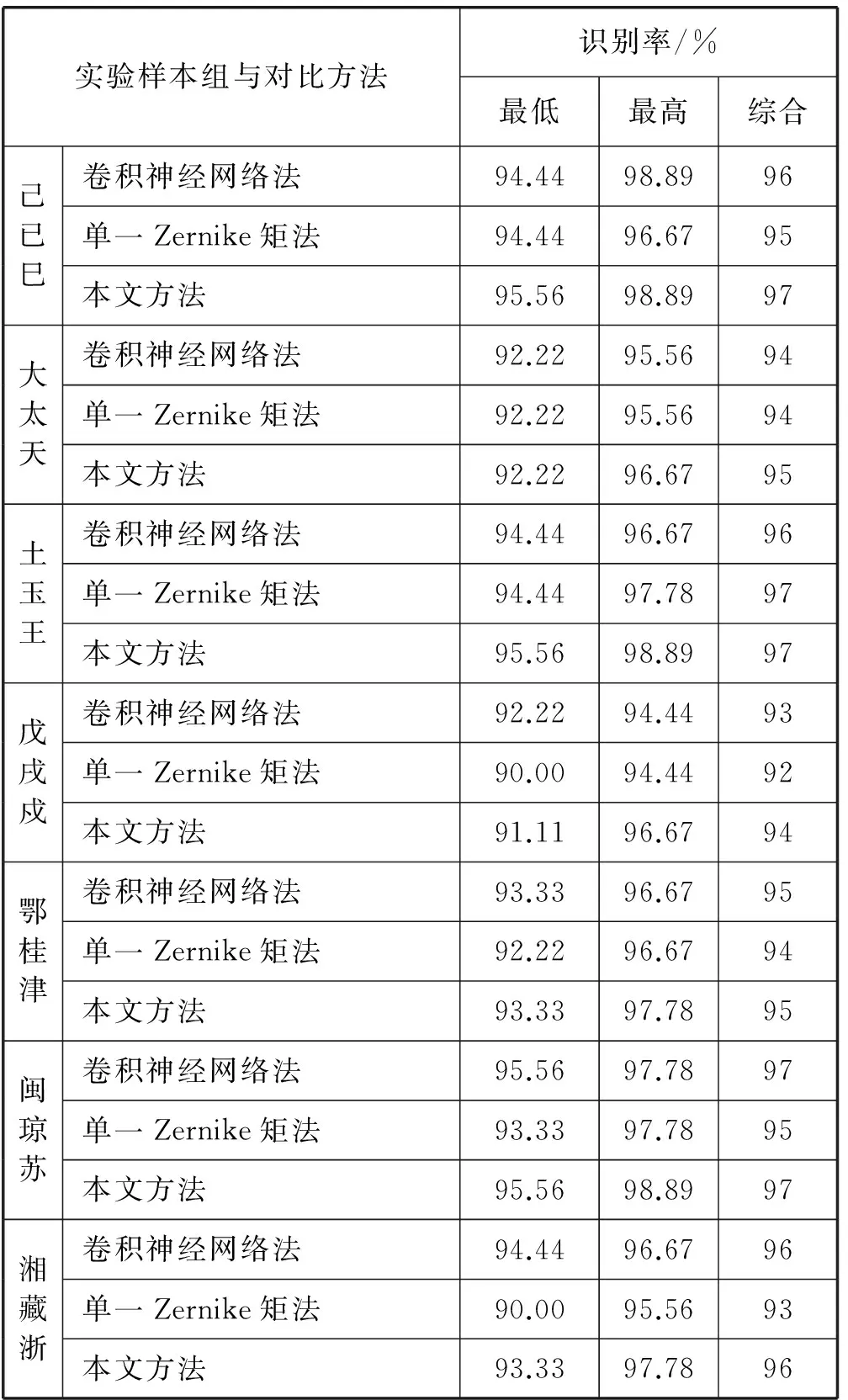
表9 均值为0,方差为0.1的高斯噪声的识别率
4.2 实验结果分析
由表1和表2可以看出,对多种类汉字一起进行分类识别时,在无噪声或噪声含量较低时,对比于单一Zernike矩法,本文方法的识别率要低1%左右。这是因为计算Zernike矩时舍弃了高频子图,造成了高频信息的丢失。而在噪声含量较高时,本文方法的识别率要高2%左右,这是消除了噪声的原因。同时,也发现用单一同类型的特征进行分类识别,得到的识别率是不稳定的,不同组之间的识别率差距较大。
另外,由表3-表9可以看出,在无噪声影响的情况下,单一Zernike矩法得到的图像特征非常完整,识别率可达99%甚至100%,卷积神经网络法的识别率与其基本相同,这说明Zernike矩法本身的准确性。由 ‘大、太、天’,‘戊、戌、戍’,‘己、已、巳’与‘土、王、玉’这四组形近汉字的实验结果可知,在相同噪声情况下,与单一Zernike矩法相比,本文方法的最低和最高识别率更好一些,最低识别率可高出3%左右,最高识别率可高出4%左右,并且综合识别率最高可高出4%左右。同时,与卷积神经网络识别法相比,本文提出的方法虽然在最低识别率上有所不足,但最高识别率以及稳定后的综合识别率却可与其持平甚至高出1%左右。另外,从‘鄂、桂、津’, ‘闽、琼、苏’与‘湘、藏、浙’这三组非形近字的实验结果可知,在相同噪声情况下,与单一Zernike矩法相比,本文提出的方法基本上还是具有更高的最低和最高识别率的,综合识别率最高也可高出3%左右。同时,与卷积神经网络识别法相比,本文提出的方法在最低识别率、最高识别率以及稳定后的综合识别率上基本可以达到卷积神经网络识别法的识别率。
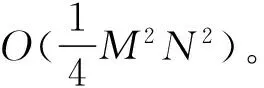
5 结 语
在单一Zernike矩法的基础上,本文提出了一种结合不可分小波四通道分解方法与Zernike矩方法的特征提取方法。从识别实验结果来看,在少种类汉字分类识别时,本文方法拥有更好的抗噪能力,较小的计算量以及高出单一的Zernike矩特征方法3%左右的识别率。同时,本文提出的方法基本上可得到与最近发展起来的具有高识别效果的卷积神经网络识别法相同的识别率以及相对较小的计算量。因此,对比这三种方法,得出本文方法是有效的。
下一步将进行多类型特征提取的研究,使用多类型特征来解决大规模多种类汉字分类问题。
[1] 刘聚宁. 印刷体汉字识别系统研究与实现[D]. 大连理工大学, 2011.
[2] 金连文, 徐秉铮. 手写体汉字识别的一种新的特征提取方法—弹性网格方向分解特征[J]. 电路与系统学报, 1997, 2(3): 7-12.
[3] 曾庆鹏, 吴水秀, 王明文. 模式识别中的特征提取研究[J]. 微计算机信息, 2008, 24(1):226-227.
[4] Hu M K. Visual pattern recognition by moment invariants[J]. Information Theory Ire Transactions on, 1962, 8(2):179-187.
[5] Khotanzad A, Hong Y H. Invariant Image Recognition by Zernike Moments[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1990, 12(5):489-497.
[6] 刘斌, 孙斌, 余方超,等. 基于不可分小波分解的图像配准方法[J]. 计算机工程, 2014, 40(10):252-257.
[7] 刘斌, 高强. 基于二维不可分小波变换的矩不变量[J]. 电子与信息学报, 2016, 38(8): 2085-2090.
[8] 黄倩文. 基于不可分小波的数字图像盲取证方法研究[D]. 湖北大学, 2013.
[9] Daubechies I. Orthonormal bases of compactly supported wavelets[J]. Communications on Pureand Applied Mathematics, 1988, 41: 909-996.
[10] Chen Q, Micchelli C A, Peng S, et al. Multivariate Filter Banks Having Matrix Factorizations[J]. Siam Journal on Matrix Analysis & Applications, 2004, 25(2):517-531.
[11] 李响, 谭南林, 李国正,等. 基于Zernike矩的人眼定位与状态识别[J]. 电子测量与仪器学报, 2015, 29(3): 390-398.
[12] 陈盈, 郑洪源, 丁秋林. 基于Zernike矩和NSCT-SVD的数字水印算法研究[J]. 计算机科学, 2016, 43(8): 84-88.
[13] 孙彩虹. 自然场景中路牌汉字识别技术研究[D]. 南京理工大学, 2014.
[14] 盛家川. 基于小波变换的国画特征提取及分类[J]. 计算机科学, 2014, 41(2): 317-319.
[15] Daubechies I, Heil C. Ten lectures on wavelets[M]. Philadelophia, PA: SIAM, 1992.
[16] Deng A W, Wei C H, Gwo C Y. Stable, fast computation of high-order Zernike moments using a recursive method[J]. Pattern Recognition, 2016, 56(C):16-25.
[17] Wang Y, Zhao Y, Chen Y. Texture classification using rotation invariant models on integrated local binary pattern and Zernike moments[J]. Eurasip Journal on Advances in Signal Processing, 2014(1):182.
[18] Nebauer C. Evaluation of convolutional neural networks for visual recognition[J]. IEEE Transactions on Neural Networks, 1998, 9(4):685-694.
[19] 葛明涛, 王小丽, 潘立武. 基于多重卷积神经网络的大模式联机手写文字识别[J]. 现代电子技术, 2014, 37(20): 21-26.
[20] 赵志宏, 杨绍普, 马增强. 基于卷积神经网络LeNet-5的车牌字符识别研究[J]. 系统仿真学报, 2010, 22(3):638-641.

