一种自适应波束赋形的大规模MIMO信道估计方法

徐啸涛 陈丽琴 朱 燕

1(浙江机电职业技术学院 浙江 杭州 310053) 2(浙江商业职业技术学院 浙江 杭州 310053) 3(诺基亚通信系统技术(北京)有限公司浙江分公司 浙江 杭州 310053)

0 引 言

大规模多输入多输出(Massive MIMO)技术是未来5G通信网络的关键技术，它能够利用简单的信号处理来实现高空间分辨率和高频谱效率。目前大量的研究工作[1,9]已经得出了大规模MIMO技术的物理信道具有简单唯一稀疏特性——有效自由度数量小于空间维度数量。这个特性在诸如毫米波的高载波频率下表现尤为显著，因此稀疏性特征被广泛应用于开发大规模MIMO的信道估计和预编码算法。信道估计方法的主要难点是利用信道稀疏特性来最小化训练导频数但同时又要保持可靠的估计精度。例如，在文献[3]和文献[4]的研究算法中，提出了波束空间信令的压缩感知方法对毫米波大规模MIMO信道进行信道估计和预编码，但是效果不尽理想。

在本文中，我们的关注点不是波束赋形的策略，而是如何基于自适应波束赋形来优化稀疏矩阵，增强信道稀疏性。这种新型的信道估计方法主要是用大量的函数研究来规划压缩感知问题，关键点是基于Kronecker的函数模型和随机特性来联合优化信道的稀疏表征。

1 系统原理模型

MIMO信道可以被建模为块衰落窄带簇信道，图1为大规模MIMO信道估计的原理图。x(M⊗1矢量)是FFT后的接收信号:

(1)

式中：hi(M⊗1矢量)及si分别是信号通道，用户i是传输信号，N是接收到的各单位间的干扰加噪声。

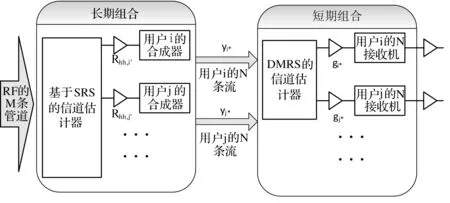
图1 大规模MIMO信道估计原理图

基于SRS的信道估计器将生成用户特定的信道协方差矩阵:

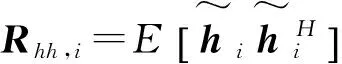
(2)

如果MIMO规模较大，Rhh,i则是较大的矩阵。因为特征向量的直接计算太复杂，所以M个天线元素被划分为N个组，其中组内天线元素间有很高的相互关联度。在天线被进行标记索引之后，信道协方差矩阵：

(3)

(4)

如果组内的相关程度在所有组中都是非常相似的，则计算复杂度可进一步减小：

wLT,i,1=wLT,i,2=…=wLT,i,N

(5)

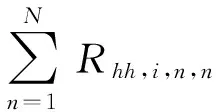
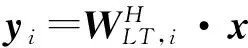
(6)

如果多用户接收器对两个用户进行短期组合，例如用户i和用户j，则可以进行联合多用户检测以更好地抑制用户间的干扰，甚至当这两个用户在空间域中并没有很好地进行分离也可以采用这种方法进行检测[2]。

(7)

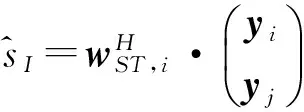
(8)

显然，联合多用户检测的方法需要的复杂度更高(一个2N⊗2N矩阵求逆与两个N⊗N矩阵求逆)。但配对的要求可以降低，并且系统的容量也可能得以扩大。

2 信道估计算法

在本节中，提出了一种潜在的自适应波束赋形的信道估计检测算法，以在大规模的MIMO系统上进行应用。此设计旨在提高可耐受性以保证复杂的计算能够顺畅进行，并尽可能重复使用当前的产品设计。

2.1 导频分离技术

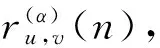
(9)

ns时隙中的循环移位αλ：

(10)

式中：

(11)

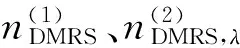
因为每个单层和在并行DMRS中排队的用户表示相同基ru,v(n)序列的循环移位版本，所以在算法中实现以下基于FFT和DCT的导频分离技术：对于具有ncs,λ=6的2个层，采用直接频域处理和最小平方(LS)的方法是可以实现的。

对于具有ncs,λ=6的两层，分离方案对应于长度为2的沃尔什-哈达玛编码。因此，通过处理两个连续的子载波，即求和(第一层)和相减(第二层)来实现导频分离。该导频分离对于恒定频域(FD)信道系数(时域中的单个路径)是理想的。而对于多径传播信道，FD系数并不是完全恒定的，但是对于具有有限延迟扩展的信道模型，FD系数是足够恒定的，以便能够仅在降级有限的情况下实现良好的分离。时域中的其他导频分离方法也可以被描述为FD中的(循环)卷积，其中FD系数通常比两个子载波跨越的范围更宽，因此涉及的子载波还更远(以及更少相关)。在这种情况下，层分离的效果可能更差，但有用层的失真度可能更小。

2.2 算法优化

上述导频分离技术算法优化问题在前期研究成果[7]中已被普遍所知，并有许多算法可计算稀疏特征向量。前期研究成果[5]也承认增强稀疏性的关键是优化矢量。因此，我们专注于用大规模MIMO信道估计并联合优化稀疏矢量和矩阵函数。

假设X在接收机处已知，H具有稀疏表征。可以用公式表示如下:

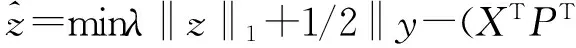
(12)

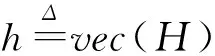
上述波束赋形的信道估计算法优化问题在前期研究成果[8]中已被普遍所知，并用此算法可计算向量z。但是增强稀疏特性的关键是优化式(12)中的Φ。因此，提出了一种自适应的波束赋形信道估计算法来进一步优化MIMO稀疏矢量和矩阵函数。

鉴于无噪声观察y，令R=NcNp是路径的总数。作为式(12)的解，R稀疏向量z的充分条件由下式给出:

NM≥(2R-1)/(δ1δ2)

(13)

式中：δ1和δ2是AoD和AoA分离的最小下限。

在所有可能的z内，如果:

(14)

则获得由z表示的h的最稀疏矢量值。针对L1范数是对L0范数矢量矩阵映射法则，可以得出:

(15)

式(15)表明，最稀疏的矢量和矩阵函数求解可以通过寻找减少稀疏矢量的L1范数来找到。首先我们初始化NtMt得到Φ值。如果关于所有信道路径的AoA和AoD的先验信息是已知的，那么这些参数可以被利用求解。如果先验信息是未知的，可以选择跨越二维间隔(0,1)⊗(0,1)的设定点作为均匀网格。然后用固定的Φ最小化式(12)以获得矢量z的信道估计。最后我们通过不断随机化更新z，并交替最后两个过程直到收敛到最小范数值。

随机化是自适应波束赋形信道估计算法的关键。在此方法中，根据式(13)，在第k次迭代，用固定的Φ最小化式(12)之后，|zk,i|的值越高，第i个矢量矩阵值在信道中合成的概率就越高。因此，算法的策略是增加高权重的矢量矩阵值周围的粒子密度，例如通过在颗粒过滤器中对粒子与其重量成比例的重新采样并通过高斯过程随机化来进行，从而在最具代表性的粒子周围产生更高浓度的粒子，以使得算法的信道估计值更加精确。

3 仿真结果分析

在本节中，通过仿真来具体分析该算法对于整体性能的改进，假设在60 GHz载频上工作的大规模MIMO系统，其中在发射机和接收机侧都使用均匀线性阵列。考虑N=16和M=64，通过随机选择Nt和Mt列，从单位矩阵获得波束赋形P和组合矩阵W。此外，为了同时发出所有信道方向，我们定义X=I·Nt。信道由每个方向的Nc=2个簇和Np=3个路径组成。对于每个簇，在[0,2π]内选择具有均匀分布的AoA和AoD的平均值，并且方差为σ2=10 deg2。噪声功率为-80 dBm。最后，通过使用分层重采样策略，随机化方法能被执行，并且为了生成新的粒子，考虑具有零均值和方差σ2u1=0.5/N,σ2u2=0.5/M的二维高斯模型。循环中的最大迭代次数为10。

在图2中，○线和╁线表示在相同的设置(Mt=M，Nt=N)下，改进型的自适应波束赋形的信道估计算法和经典傅里叶基本稀疏信道估计算法在不同h值信噪比下RMSE(均匀功率分配频谱效率评估归一化均方根)的值。为了比较，我们用精确的信道信息来计算频谱效率，可以看出我们所提出的自适应波束赋形信道估计算法对噪声抑制更加稳定。而且随着信道信噪比的增加，此算法对于噪声抑制的效果更为明显。在此设置中，也提出了在经典傅里叶基本稀疏信道估计上对20 dB的净改进，增益近似恒定在10 dB。

图2 不同算法下基于SNR函数的RMSE值

为了便于研究噪声影响，图3、图4分别考虑SNR在2个水平(10 dB， 20 dB)下，作为传输数量Nt(Mt=M)函数的频谱效率。从图中可以得出，对于具体确定选择的波束，多用户大规模MIMO信道估计仍然工作，但是需要更高的SNR支持。当信道PRB数增加时，DCT和FFT之间的差距会逐渐变小。从图中也可以看出本文所提出的自适应波束赋形信道估计算法显示了对典型波束赋形算法性能有显著的改进。 仿真结果表明，这种新型的算法对噪声具有较强的鲁棒性，并且相对于普通的波束空间信令压缩感知算法，训练导频数目显著减少。

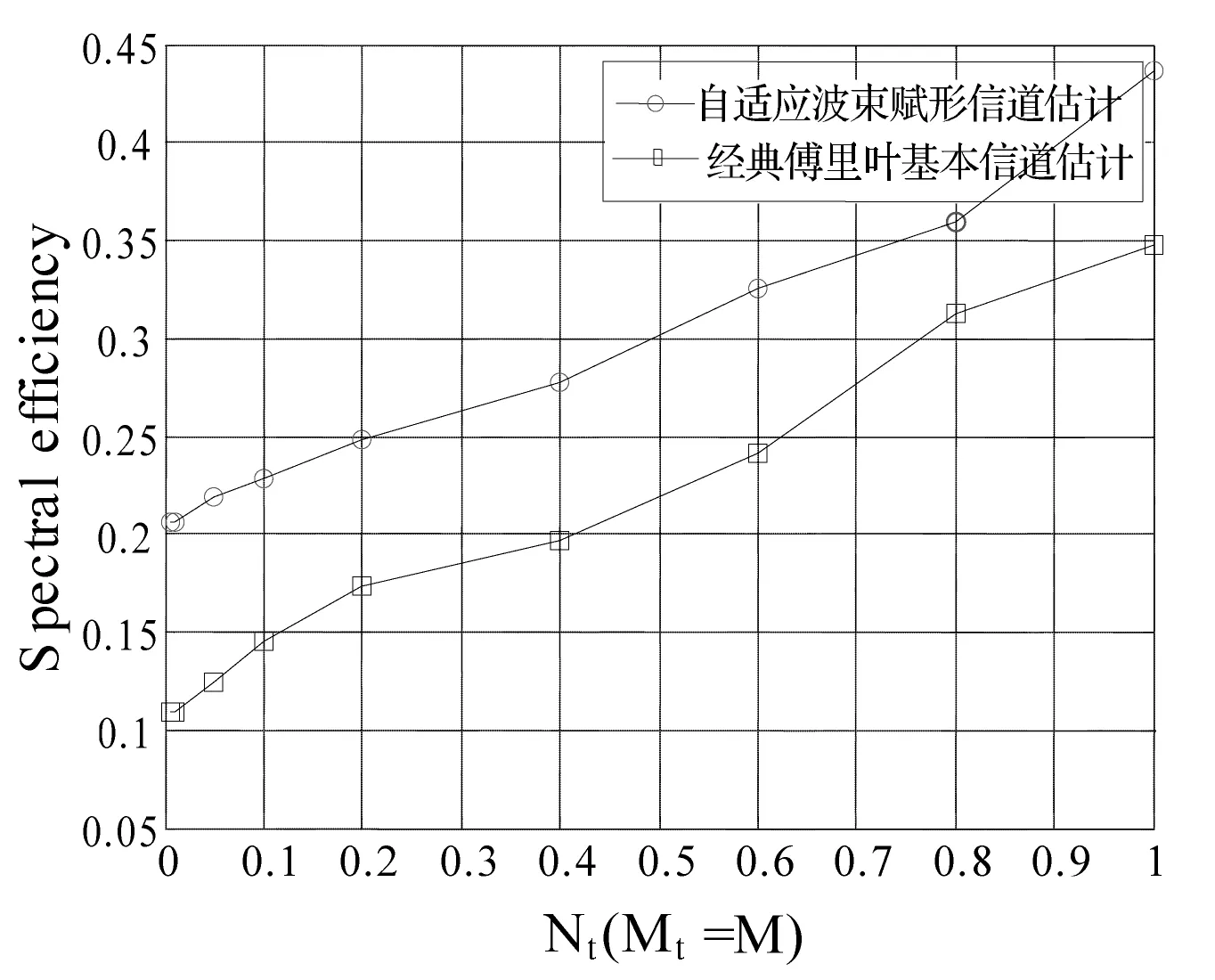
图3 SNR=10 dB时Nt(Mt=M)函数的频谱效率

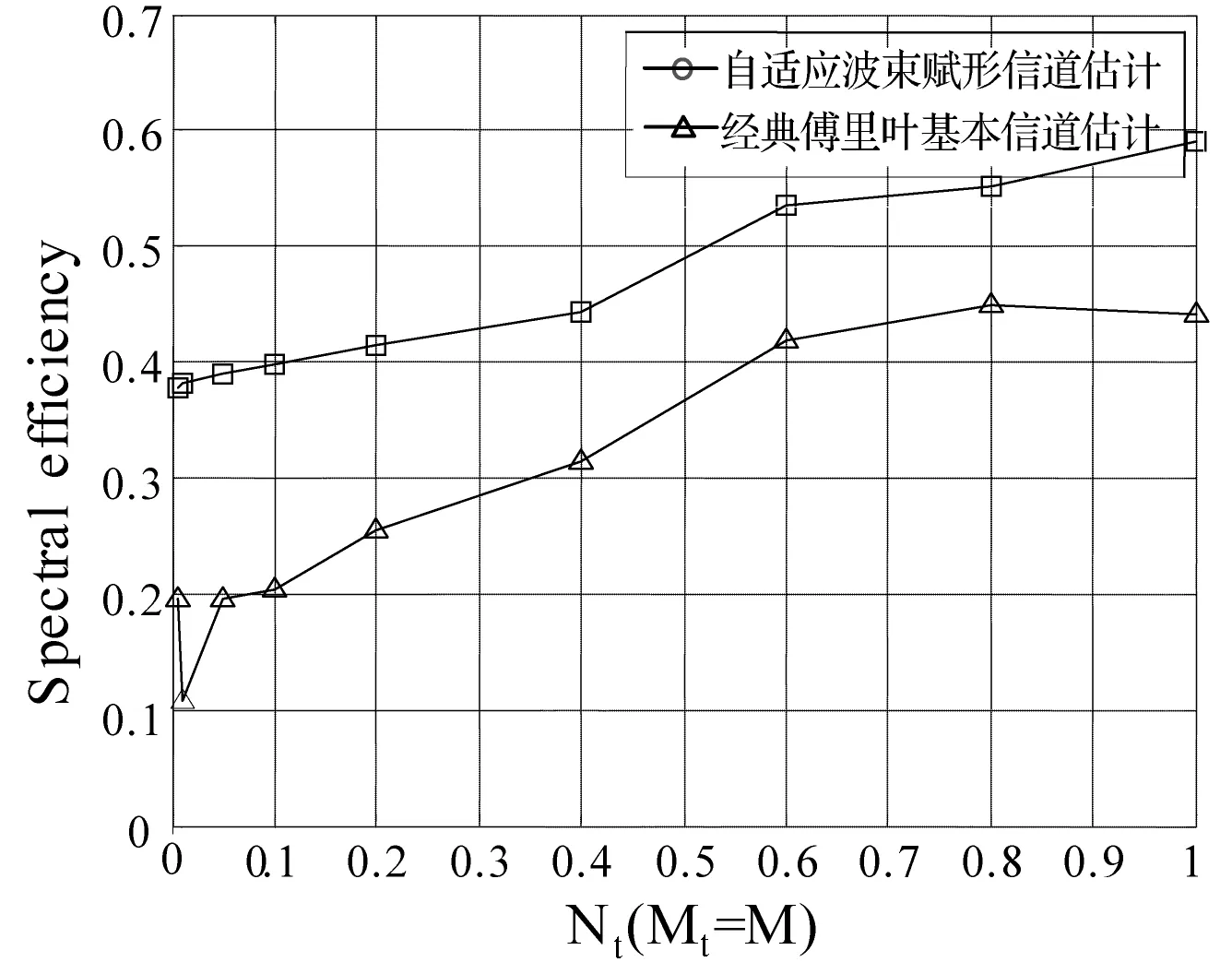
图4 SNR=20 dB时Nt(Mt=M)函数的频谱效率

4 结 论

本文提出了一种用于大规模MIMO的新型信道估计算法，即自适应波束赋形信道估计算法。这种技术的核心是如何基于自适应波束赋形来优化稀疏矩阵，增强信道稀疏性。这种新型的信道估计方法主要是用大量的函数研究来规划压缩感知问题，关键点是计算稀疏矢量和基于重采样的矢量随机化之间的交换。即使是次优的，这种最小化策略也具有低复杂性和高效的特点。虽然对经典傅里叶波束赋形算法进行了实质性改进，但针对文中导频分离技术引起测量噪声的问题。下一步我们仍然要对技术方法进一步优化，从而改善导频分离时噪声抑制性能。

[1] 胡安中. 大规模MIMO系统的信道与DOA估计研究[D]. 北京邮电大学，2014.

[2] Rusek F, Persson D, Lau B K, et al. Scaling up MIMO: opportunities and challenges with very large arrays [J]. IEEE Signal Processing Magazine, 2012, 30(1): 40-60.

[3] 胡培利，何雪云，梁彦. 一种基于压缩感知的大规模MIMO信道估计中导频优化设计新方法[J]. 南京邮电大学学报，2016，36(5)：38-42.

[4] 张涵，郭昌霖，李家明，等. 基于混合导频辅助的大规模MIMO上行链路信道估计[J]. 华南师范大学学报，2016，48(6)：57-62.

[5] 赵迎芝，唐宏，叶宗刚，等.多用户大规模MIMO系统中能效的研究[J].重庆邮电大学学报，2016，28(5)：737-742.

[6] Hu Ying，Huang Yongming，Yu Fei，et al. Energy-efficient resource allocation based on multi-user massive MIMO system[J]. Journal of Electronics&Information-Technology, 2015, 37( 9) : 2198-2203.

[7] 陶成，李亚鹏，刘留，等. 莱斯信道下大规模MIMO系统上行资源分配研究[J]. 北京交通大学学报，2016，40(5)：50-55.

[8] 王毅, 钱叶旺, 林艳,等. 时间相关信道下分布式大规模 MIMO系统频谱效率分析[J]. 信号处理, 2016, 32(11):1269-1282.

[9] 冯文, 周斌, 郑敏,等. 大规模MIMO系统的信道估计研究[J]. 计算机应用与软件, 2016, 33(12):89-92.