UTM投影变形分析及解决方案

杨 帆 嵇建扣 丁 盼

（中交第四航务工程勘察设计院有限公司 广东广州 510230）

1 前言

球面是一个不可直接展成平面的曲面，因此无论采用什么投影方法，投影面上得到经纬网的形状与球面上的经纬网形状不完全相同。这表明地图上的经纬网发生了变形。因而根据地理坐标展绘在地图上的各种地物，也必然发生了形变，为了正确使用地图，必须了解投影后产生的变形，所以投影变形问题是地图投影的重要组成部分。通用横轴墨卡托投影(UTM投影)是与高斯-克吕格投影极为相似的一种投影，但它与常用的高斯-克吕格投影存在一定的差异[3]。WGS84坐标系和UTM投影方法（Universal Transverse Mercator Projection，通用横轴墨卡托投影）是世界许多国家采用作为该国家的坐标系统和投影方式。

印尼爪哇某工程位于印度尼西亚芝勒贡市，该项目正式运营后将有效的解决芝勒贡市周边地区的缺电情况。项目海上主体部分设计拟采用4公里引桥连接码头和陆域电厂方案，引桥和码头主体完成之后，采用管带机将船只运输的燃煤从码头运输到陆域电厂厂区，该设计有效避免了当地淤泥浅水区对船只通行的影响，并大大地减小运营后疏浚的成本。

图1 海上工程主体效果图

为满足本工程初步设计阶段的需要，需要对上述工程所在的区域进行陆域及海上地形测量及控制测量等工作。

2 坐标系统及投影变形

根据 GB 50026—2007 《工程测量规范》3.1.4 之规定：平面控制网的坐标系统，应满足测区内投影长度变形不大于 2.5 cm ／km[1]。

以UTM投影为例，地面水平距离S0归算到参考椭球面上的投影变形：

参考椭球面上边长S归算到高斯平面的投影变形：

地面水平距离S0按照UTM投影的长度总变形：

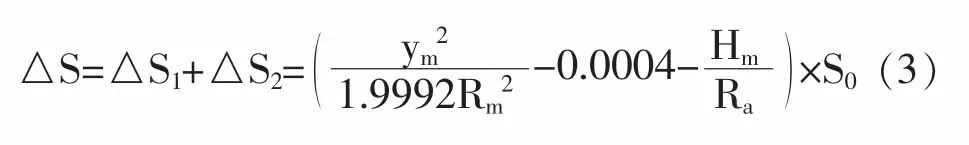
而高斯投影长度总变形：

式中：S0为实测地面水平距离（m）；ym为测距边两端点横坐标平均值 (km)；Rm为测距边中点的平均曲率半径 (km)；Hm为测距边两端相对于参考椭球面的平均大地高程(m)；Ra为归算边方向法截弧曲率半径(m);M为子午圈曲率半径(km)；N为卯酉圈曲率半径(km)。为了研究选择不同的中央子午线的变化而造成投影变形大小情况，以本项目为例，取平均纬度为6°，测区平均高程为5m，投影面高程为0，Ra=R=6378km。本文只考虑长度投影变形的绝对值，研究高斯投影和UTM投影随离中央子午线不同距离情况下的投影变形绝对量。

将表1长度投影变形值统计表进行绘图连线，我们可以生成投影变形示意图，见图2。

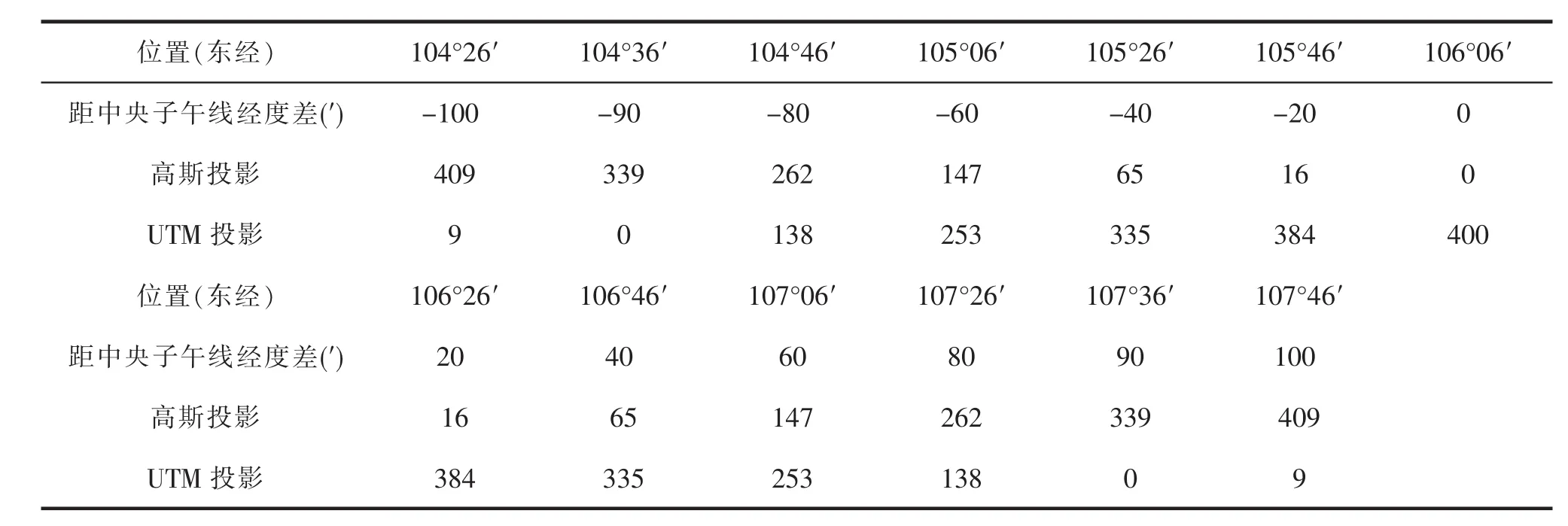
表1 长度投影变形绝对量统计

图2 投影变形比较示意图

通过表1和图2，我们知道UTM投影和高斯投影区别较大，相距中央子午线经度差为0时，UTM投影变形达到40cm，而高斯投影在此处投影变形值为0；相反，离中央子午线越远，高斯投影投影变形值越大，UTM投影则在0~1°30′区间是越来越小，越过临界处1°30′之后则越来越大。

3 坐标系统及投影变形解决方案

3.1 投影变形分析

该项目坐标系统采用WGS84坐标系，UTM投影，48M区域，项目所在区域中心经度约为东经106°06′，中央子午线为 105E°。 根据公式（1）~（4）进行计算，该项目区域范围内投影变形量1 km约22 cm，远超过规范规定的1 km 2.5 cm。因为本项目海上工程主体部分采用长引桥方案，长引桥总长约4 km长。如果本项目仍继续采用此坐标系统，则投影变形造成的距离总误差约88 cm，这对整个项目的建设以及后续与陆域的设备安装和拼接都将产生非常大的影响。

特别针对电厂海工主体部分采用长引桥方案，为了尽量减小本项目投影对主体施工及引桥管带机安装拼接的问题，我们对本地区的投影变形进行分析和研究。

经过表3我们可以发现，该地区标准UTM投影变形下的控制点坐标反算边长与全站仪实测距离1 km相差约22 cm，这点与我们通过投影变形理论计算公式结果基本一致。

3.2 解决投影变形方案

解决投影变形常见的方案有多种：更改投影比例参数，更改投影面高程和更改投影中央子午线。各种方法基本准则都是一样，都是为了保证控制点投影后的平面坐标反算距离与实际边长距离一致。

本项目建立电厂独立坐标系，方法是：在现有的坐标系统WGS84坐标系，UTM投影48M区域基础之上，只将投影中央子午线由105E°更改为104°36′E，其余的投影参数（椭球参数，比例尺参数等）保持不变，从而实现最小投影变形。表2为部分控制点成果，包含标准UTM投影坐标的WGS84坐标和更换中央子午线后投影的独立坐标。

表2 控制点成果表

表3 边长检测成果

同时，通过表3我们还可以发现我们建立的独立坐标系反算距离与全站仪实测边长结果基本一致。证明我们创建的独立坐标系投影变形较小。通过同名点不同坐标系的坐标，采用四参数坐标转换模型计算出平面坐标转换关系参数，公式如下：

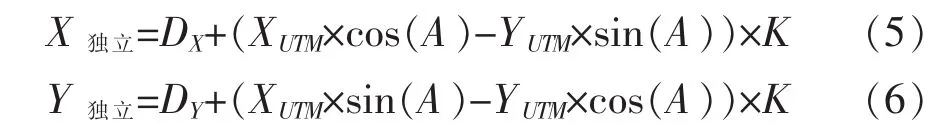
根据(5)式和（6）式我们可以计算出由标准UTM投影坐标到独立坐标系坐标的四个参数：平移参数DX和DY，以及旋转角度A，和比例因子K。最后根据四参数，我们将标准UTM投影的地形图再转换得到没有投影的独立坐标系下的地形图，从而有效的解决了投影变形问题，保证控制点投影后的平面坐标反算距离与实际距离基本一致。

4 结束语

对地图投影变形有了更深刻和清晰的认识，为了减小投影变形对工程项目的影响建立无投影变形的工程坐标系是十分必要的。解决UTM投影变形方案原理基本是采用建立独立坐标系方法，使得投影变形满足规范要求，并计算得出独立坐标系和UTM坐标系之间的转换关系，从而有效解决投影变形带给工程的影响，指导意义如下：

（1）在海外工程项目中，设计及勘测技术人员应该重视UTM投影变形对工程项目的影响，应及早建立独立坐标系，避免投影变形造成后续施工构造物的连接问题以及构筑物尺寸位置和坐标的竣工验收问题。

（2）为海外测量人员提供了一种解决UTM投影变形的有效方法，并通过实际工程案例验证了这一方法切实可行，为类似工程项目提供借鉴。

参考文献：

[1]贾登科，麦若绵，朱国锋.欠发达国家坐标系统及平面控制有关问题探讨；[J].水运工程，2013(7)121-125.

[2]叶达忠，谢家业，龙华.国际工程测量的UTM投影变形及抵偿分析[J]广西师范学院学报(自然科学版)，2009(3)91-93.

[3]袁小勇，陈功，易袜.国际工程中UTM投影变形的应对策略[J]工程勘察，2010(5)71-75.