多因素条件下单级齿轮系统的非线性特性

彭毓敏 马 超 栾忠权 徐小力

北京信息科技大学现代测控技术教育部重点实验室，北京，100192

0 引言

齿面摩擦、齿侧间隙、啮合阻尼以及时变啮合刚度等影响因素使得齿轮传动的动力学系统具有复杂的强非线性，这种强非线性振动对系统的安全性、稳定性、可靠性及工作性能有很大的影响，实际应用中，我们应该从各个方面来减小这种不利的影响。基于此，国内外学者对齿轮传动系统的非线性现象做了大量的研究与分析[1-9]。何航红[10]建立了齿侧间隙变化的齿轮传动系统非线性动力学模型，探讨了不同齿侧间隙下的齿轮传动系统吸引子的变化。陈思雨等[11]建立了常间隙、时变间隙和随机间隙三种不同的间隙形式，利用数值仿真的方法研究了轮齿间隙对齿轮系统动力学响应的影响。王帅宝等[12]基于 Poincare 映射，建立了二自由度齿轮传动系统的数学模型，并通过数值仿真说明齿轮传动系统存在倍周期分岔、Hopf 分岔和混沌等复杂的非线性现象。盛冬平等[13]采用集中质量法建立了齿轮-转子-轴承系统的六自由度多间隙弯扭耦合的非线性振动模型，研究了齿面摩擦、时变啮合刚度、齿侧间隙和支撑间隙等因素对系统分岔特性的影响。

目前进行的理论研究多是分析纯扭转齿轮振动模型，或在弯扭耦合模型中分析啮合频率的变化，或在齿侧间隙不变的情况下分析对系统动力学特性的影响。本文以三自由度的多间隙弯扭耦合的非线性动力学模型为研究对象，模型考虑了齿轮系统阻尼、啮合刚度、齿侧间隙及轴承支撑间隙，综合分析了齿侧间隙、轴承支撑间隙耦合下，激励频率变化对系统动力学特性的影响；激励频率一定条件下，齿侧间隙、轴承支撑间隙偶合变化对系统动力学特性的影响。运用分岔图、时间历程图、相平面图、Poincare图、频谱图，分析参数变化对齿轮系统稳态响应的影响，总结齿轮系统的周期运动和混沌运动。

1 齿轮非线性动力学模型

对于单对齿轮副的齿轮-转子-轴承系统，假设传动轴和轴承均对称于齿轮的中心平面，系统可以处理成为具有3个自由度的平面弯-扭耦合振动系统，建立其动力学模型。如图1所示，3个自由度分别为齿轮绕旋转中心的转动自由度和主动、被动齿轮y方向上的平移自由度。

图1 系统动力学模型Fig.1 Dynamic model for gear train

图1中，下标1、2分别代表主动齿轮、被动齿轮。其中，θi(i=1，2)为齿轮的扭转振动位移，yi为齿轮y方向的振动位移，ri为齿轮的基圆半径。由于不考虑传动轴等的具体振动形式，故可将传动轴、轴承和箱体等的支撑刚度和阻尼用组合等效值k1、k2和c1、c2来表示，啮合阻尼系数为c0，啮合刚度系数为k0。

1.1 运动微分方程建立

对于该齿轮系统，系统的动能可表示为

系统的势能可表示为

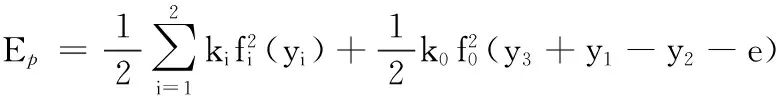
式中，f1、f2、f0为齿轮副上的间隙非线性函数；e为啮合误差。

系统的耗能可表示为

由拉格朗日方程

式中，qj为各方向的振动位移；Fj为各方向受到的作用力。

可得系统的弯扭耦合分析模型：

(1)

式中，F1、F2分别为作用在主动、被动齿轮上的动态啮合力；Fm为由激励扭矩的平均分量引起的轮齿啮合力；FaT(t)为由激励扭转的变动分量引起的轮齿啮合力。

定义动态传递误差与静态传递误差的差值y0=y3+y1-y2-e，则可将式(1)进一步简化，写成矩阵形式：

(2)

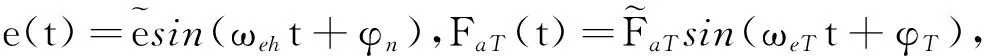
1.2 系统的量纲一方程

(3)

分析模型中的间隙非线性函数为

(4)

j=0,1,2

2 系统非线性动态特性分析

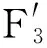
假设具有零初始位移条件，观察间隙和频率的变化对系统动力学特性的影响。

2.1 系统随激励频率变化的动力学特性

图2 齿轮系统随激励频率变化分岔图Fig.2 Bifurcation diagram by excitation frequency for gear train

(a)时间历程图 (b)相平面图

(c)Poincare图 (d)频谱图图3 =0.5的时间历程响应、相平面曲线、Poincare图和频谱图Fig.3 Time history plot, phase diagram, Poincare diagram and frequency spectrum when is 0.5

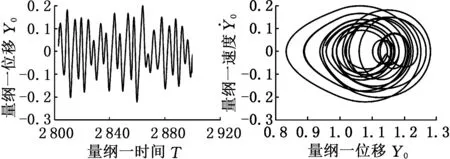
(a)时间历程图 (b)相平面图

(c)Poincare图 (d)频谱图图4 =0.65的时间历程响应、相平面曲线、Poincare图和频谱图Fig.4 Time history plot, phase diagram, Poincare diagram and frequency spectrum when is 0.65

(a)时间历程图 (b)相平面图

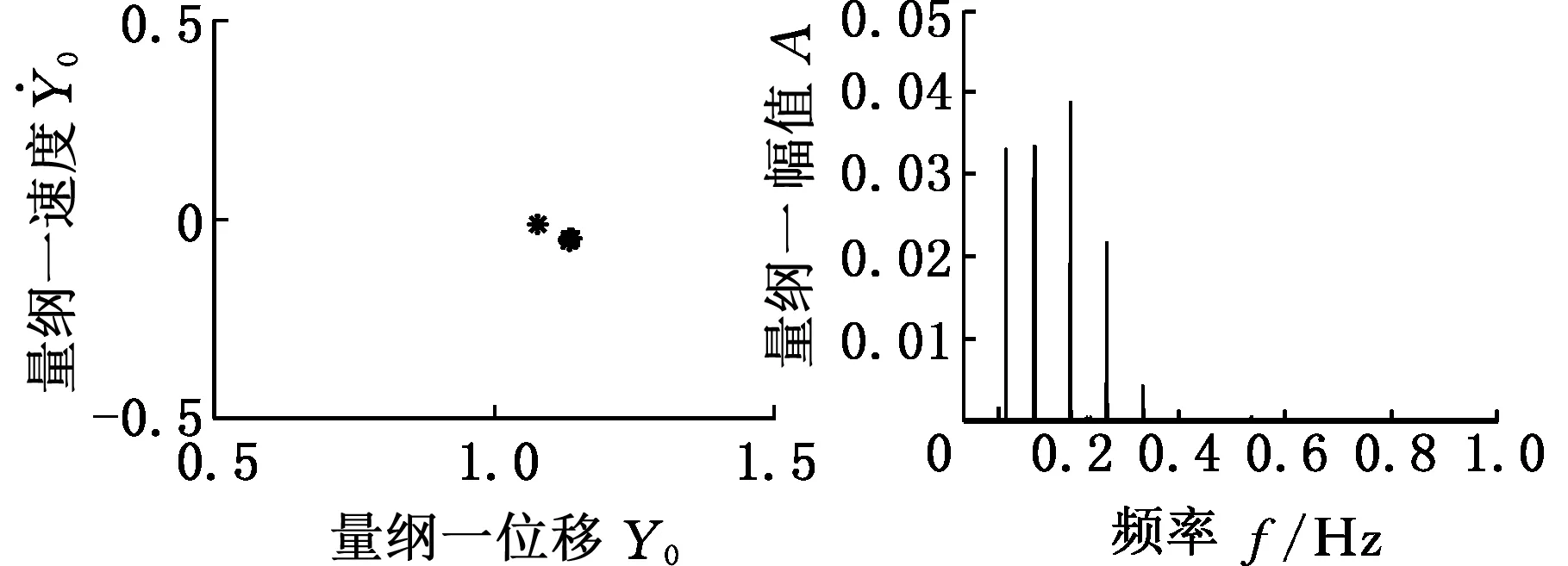
(c)Poincare图 (d)频谱图图5 =0.85的时间历程响应、相平面曲线、Poincare图和频谱图Fig.5 Time history plot, phase diagram, Poincare diagram and frequency spectrum when is 0.85

2.2 系统随齿侧间隙b0变化的动力学特性

(a)时间历程图 (b)相平面图

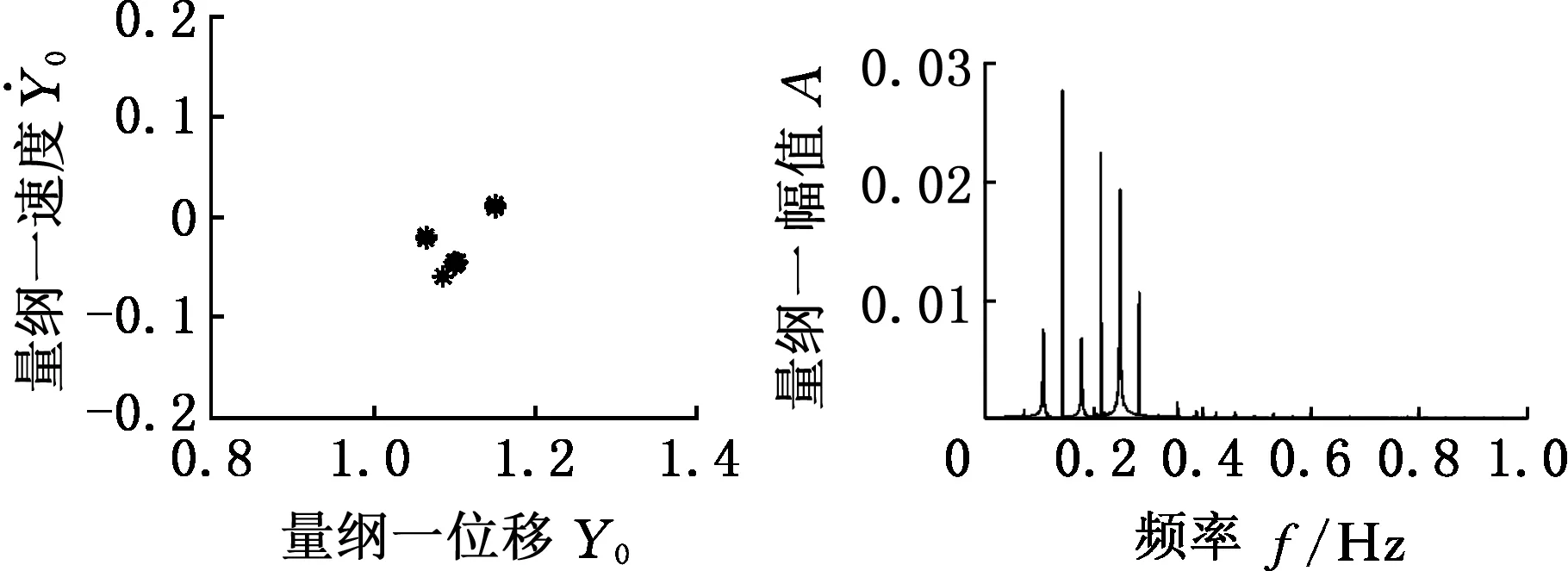
(c)Poincare图 (d)频谱图图6 =0.89的时间历程响应、相平面曲线、Poincare图和频谱图Fig.6 Time history plot, phase diagram, Poincare diagram and frequency spectrum when is 0.89

图7 =1.4时系统随齿侧间隙变化分岔图Fig.7 Bifurcation diagram by gear backlash when is 1.4

由图7可以看到，当齿侧间隙b0从大到小变化时，齿轮系统从稳定的单周期运动经倍周期分岔进入二倍周期运动，然后由二倍周期运动经激变直接进入混沌。

齿侧间隙b0=0，0.02，0.1不同时，齿轮系统的时间历程响应、相平面曲线、Poincare图和频谱图见图8～图10。

(a)时间历程图 (b)相平面图

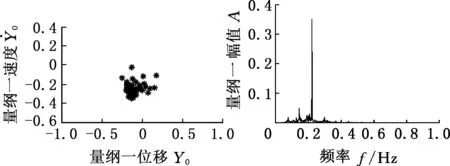
(c)Poincare图 (d)频谱图图8 b0=0的时间历程响应、相平面曲线、Poincare图和频谱图Fig.8 Time history plot, phase diagram, Poincare diagram and frequency spectrum when b0 is 0

(a)时间历程图 (b)相平面图

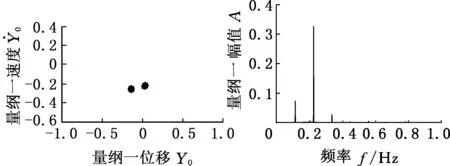
(c)Poincare图 (d)频谱图图9 b0=0.02的时间历程响应、相平面曲线、Poincare图和频谱图Fig.9 Time history plot, phase diagram, Poincare iagram and frequency spectrum when b0 is 0.02

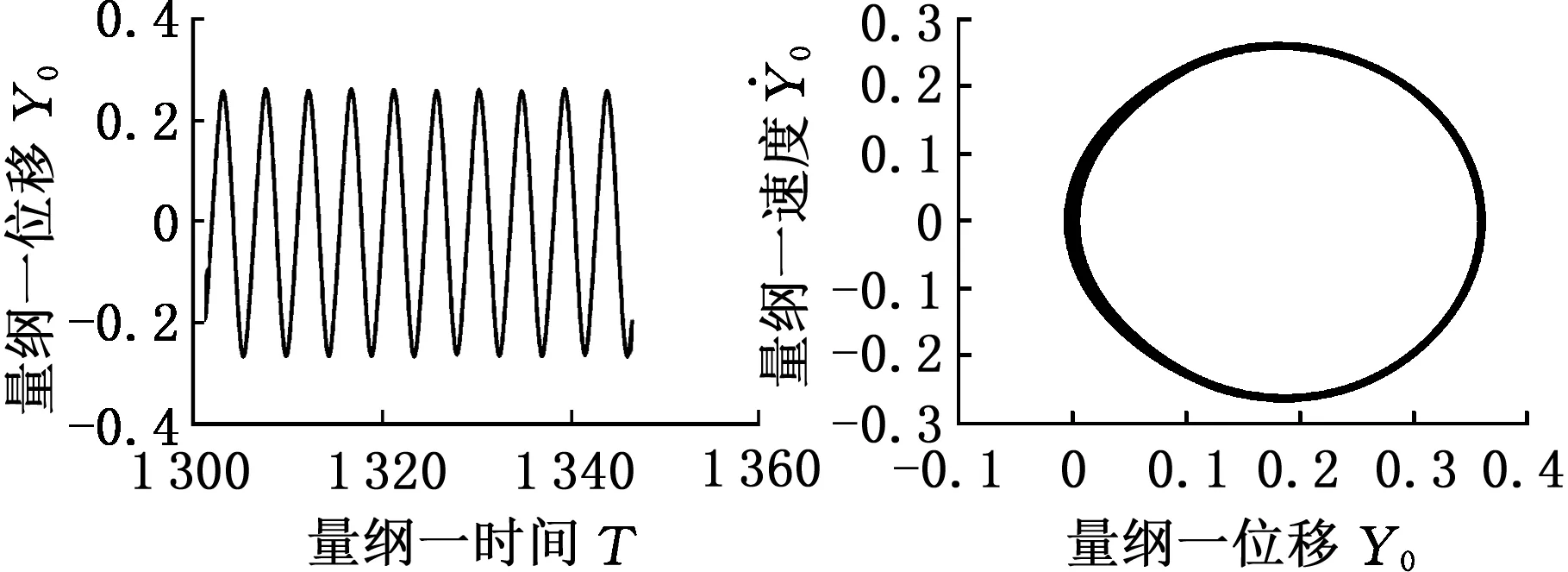
(a)时间历程图 (b)相平面图

(c)Poincare图 (d)频谱图图10 b0=0.1的时间历程响应、相平面曲线、Poincare图和频谱图Fig.10 Time history plot, phase diagram, Poincare diagram and frequency spectrum when b0 is 0.1

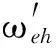
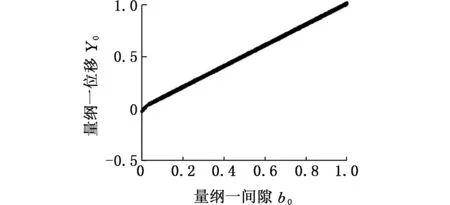
图11 =1.5时系统随齿侧间隙变化分岔图Fig.11 Bifurcation diagram by gear backlash when is 1.5

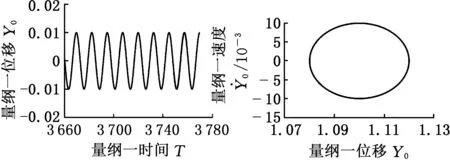
观察齿侧间隙b0=0，0.5时的齿轮系统时间历程响应、相平面曲线、Poincare图和频谱图。b0=0时的系统的时间历程响应、相平面曲线、Poincare图和频谱图为图12、图13。

(a)时间历程图 (b)相平面图

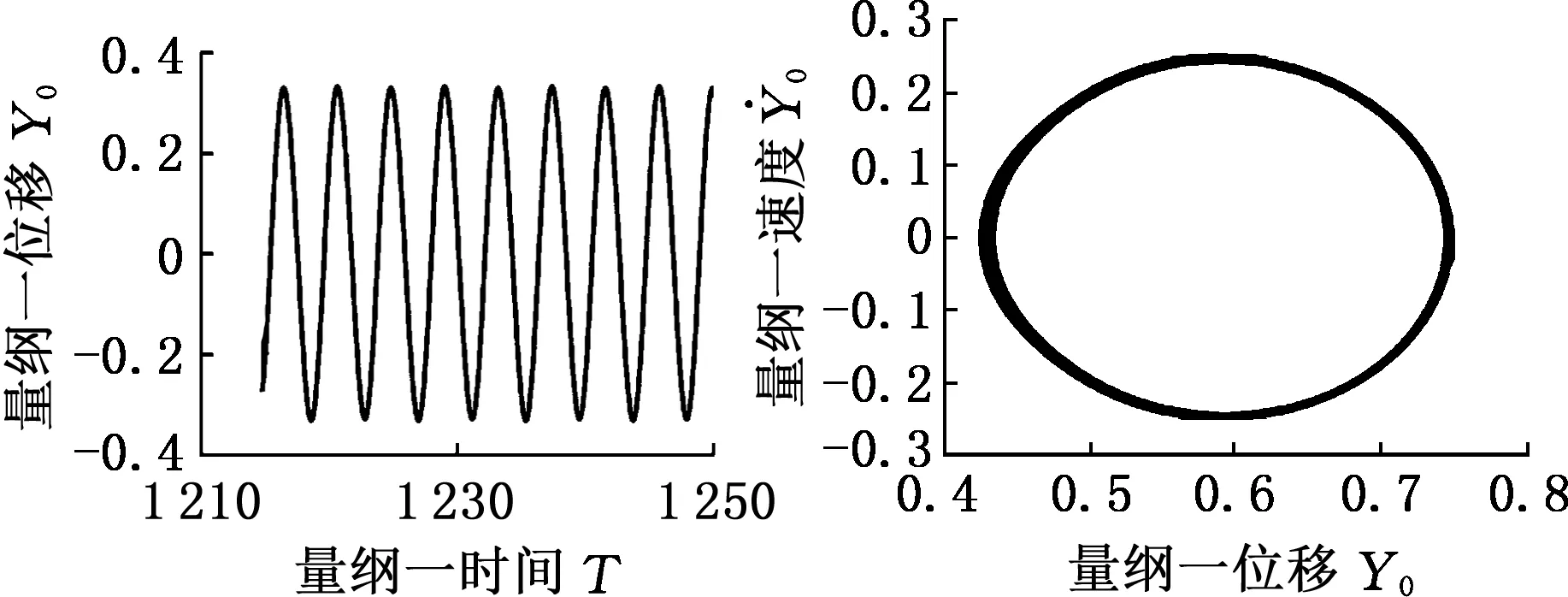
(a)时间历程图 (b)相平面图

(c)Poincare图 (d)频谱图图13 b0=0.5的时间历程响应、相平面曲线、Poincare图和频谱图Fig.13 Time history plot, phase diagram, Poincare diagram and frequency spectrum when b0 is 0.5

由图12、图13可知，b0=0.5时的齿轮系统振幅比较大，说明随着齿侧间隙的增大，齿轮系统的振动幅增大，但并没有改变齿轮系统的运动状态，系统的动态特性只有量的改变，没有发生质的影响，表明此种情况下系统的响应对间隙不敏感。

3 结论

(1)系统在固定的齿侧间隙和轴承支撑间隙下，随着激励频率的变化表现出不同的运动状态。在一定的激励频率范围内，随着激励频率的增大，系统由单周期运动状态激变为混沌运动，然后由混沌运动激变为双周期运动。随后，由双周期运动经倍周期分岔进入四周期运动，之后经历逆倍周期分岔变为双周期运动，最后变为单周期运动状态。

(2)在不同的激励频率下，齿侧间隙的变化对齿轮系统动力学特性的影响不同。在特定范围内，齿侧间隙的变化只改变系统的振动幅值，并不会改变其动力学特性。当系统处于混沌运动状态时，齿侧间隙的增大可以使系统由混沌运动变为周期运动。

参考文献：

[1] NEVZAT O H, HOUSER D R. Mathematical Models Used in Gear Dynamics—a Review [J]. Journal of Sound and Vibration,1988,121 (3) :383-411.

[2] KAHRAMAN A, SINGH R. Non-linear Dynamics of a Spur Gear Pair [J]. Journal of Sound and Vibration, 1990, 142(1):49-75.

[3] KAHRAMAN A, SINGH R. Nonlinear Dynamics of a Geared Rotor-bearing System with Multiple Clearances [J]. Journal of Sound and Vibration ,1991,144(3):469-506.

[4] KAHRAMAN A, SINGH R. Interactions between Time-varying Mesh Stiffness and Clearance Non-linearities in a Geared System [J]. Journal of Sound and Vibration, 1991,146(1):135-156.

[5] HOWARD I, JIA S, WANG J. The Dynamic Modeling of a Spur Gear in Mesh including Friction and a Crack [J]. Mech. Syst. Signal Process, 2001,15(5):831-853.

[6] THEODOSSIADES S. Non-linear Dynamics of Gear-pair Systems with Periodic Stiffness and Backlash [J]. Journal of Sound and Vibration, 2000,229(2):287-310.

[7] AL-SHYYAB A, KAHRAMAN A. Non-linear Dynamic Analysis of a Multi-mesh Gear Train Using Multi-term Harmonic Balance Method: Sub-harmonic Motions [J]. Journal of Sound and Vibration,2005,279 (1) :417-451.

[8] 苏程，黄志丹.单自由度齿轮系统的周期运动和混沌运动[J].甘肃农业大学学报，2012，47(3):134-137.

SU Cheng, HUANG Zhidan. Periodic Motions and Chaotic Motion in Single Degree of Freedom Spur Gear Pair System[J]. Journal of Gansu Agricultural University, 2012，47(3):134-137.

[9] 李英明，陈卫东，陈奇，等.齿侧间隙对齿轮副非线性振动特性的影响研究[J].机械传动，2013,37(5)：1-5.

LI Yingming, CHEN Weidong, CHEN Qi, et al. Research of the Influence of Gear Backlash on Gear Pair Nonlinear Vibration Characteristic[J]. Journal of Mechanical Transmission, 2013,37(5)：1-5.

[10] 何航红.齿侧间隙对齿轮系统动力学行为的影响[J].机械设计与制造，2012(7)：281-283.

HE Hanghong. Effect of Backlash on Dynamics Behavior of Gear System [J]. Machinery Design & Manufacture, 2012(7)：281-283.

[11] 陈思雨，唐进元. 间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响[J].机械工程学报，2009,45(8)：119-124.

CHEN Siyu, TANG Jinyuan. Effect of Backlash on Dynamics of Spur Gear Pair System with Friction and Time-varying Stiffness[J]. Journal of Mechanical Engineering, 2009,45(8)：119-124.

[12] 王帅宝，莫云辉，张黎明. 含间隙和时变啮合刚度齿轮传动系统的分岔和混沌[J].设计与研究，2009，36(5)：25-28.

WANG Shuaibao, MO Yunhui, ZHANG Liming. Bifurcation and Chaos of the Gear System with Backlash and Time-varying Mesh Stiffness[J]. Design and Research, 2009，36(5)：25-28.

[13] 盛冬平，朱如鹏，靳广虎，等.考虑摩擦的多间隙直齿弯扭振动建模和分岔特性[J].航空动力学报，2015,30(2)：498-505.

SHENG Dongping, ZHU Rupeng, JIN Guanghu, et al. Bifurcation Characteristic and Modeling of Transverse-torsional Spur Gear Vibration Considering Friction and Multiple Clearances [J]. Journal of Aerospace Power, 2015,30(2)：498-505.

[14] 李润方,王建军.齿轮系统动力学——振动、冲击、噪声[M].北京:科学出版社,1997.

LI Runfang, WANG Jianjun. Dynamics of Gear System: Vibration, Shock and Noise[M]. Beijing: Science Press,1997.