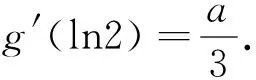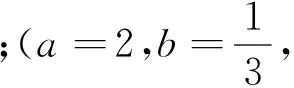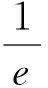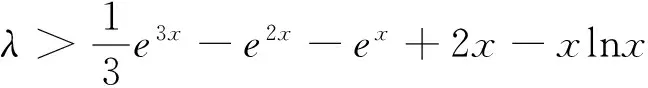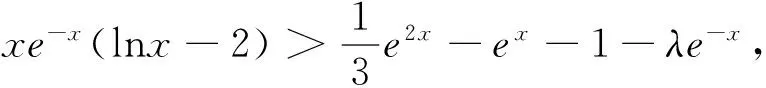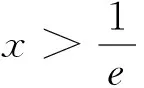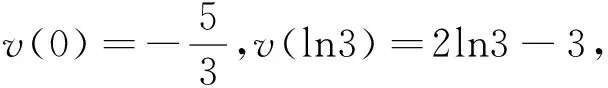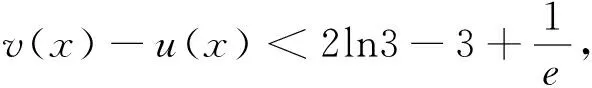分离函数法在解题中的应用
曾建强
江西省萍乡市教研室 (337000)
解决形如F(x,a)类问题,通常利用分离参数法,将原式变形为变量与参数各在一边的f(x)≥a或f(x)≥g(a)等形式,从而求解,已为熟知的解题通法.而有一些含参数的问题其参数a不能从解析式F(x,a)中分离出来,或F(x,a)中常为含两个超越函数的关系,解决时由于不同类超越函数不便变形化简研究性质,可尝试用分离函数的方法来处理.
所谓分离函数法,是指将同一关系F(x,a)中的两类不同函数(尤其是两不同超越函数)分离开来或把问题分离成f(x),g(x,a)(或f(x,a),g(x,a))两类关系来分别处理的方法.分离函数法,主要是利用分离后的两函数的最值性质来解.
分离函数方法是高中数学中“新兴”的一种解题方法,这里举几例以飨读者.
一、不同变元的分离函数
对一个关系式中有两不同变元,由于两变元的独立性,故分离出不同变元的两函数进行研究势在必行.
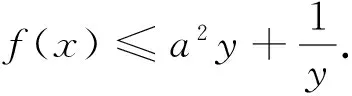
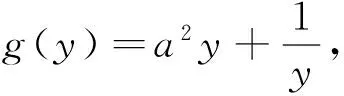
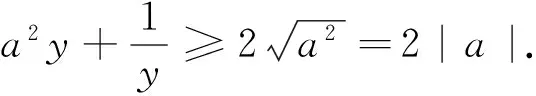
二、单式中的分离函数
对一个变量的问题,往往容易从单式的整体着手研究,但将单式分离成两个不同函数分别研究,这种思路比较隐蔽,却也是一法.
例2 证明:x∈R,a≤1时,xex+a+x2-2x+1>0.
分析:将不等式左边看成是一个函数,至少要求二阶导数才有可能确定它的值域,事实上仍很困难.如果将一个函数分离成两个函数,突破f(x)=xex+a求导产生的难点,也是处理问题的一策.这种化整体为多个体的策略,有时还很奏效.
证明:要证原式,通过分离函数,即证xex+a>-(x-1)2.①
当x>0时,xex+a>0,-(x-1)2≤0,显然①式成立.
当x≤0时,f(x)=xex+a的导数f′(x)=(x+1)ex+a,易得f(x)min=f(-1)=-ea-1.
而g(x)=-(x-1)2(x≤0)的最大值为g(0)=-1.
由于a≤1,有ea-1≤1,且两函数不在同一处取到最值,故x≤0时xex+a>-(x-1)2.
综上,原不等式成立.
三、不同两类基本函数的分离
含不同两类基本函数相对较复杂,且常是不同类超越函数的复合函数,就是利用导数这个有力的工具,有时也难避免由于导数的复杂性使得求解中途受阻.化繁为简是我们常用的思路,尤其对两个超越函数的混合型函数更加突出,分离函数就显得尤为重要.
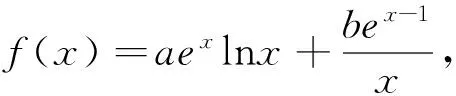
(Ⅰ)求a,b;(a=1,b=2解略.)
(Ⅱ)证明:f(x)>1.
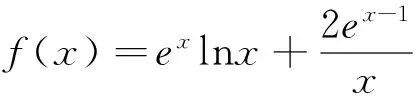
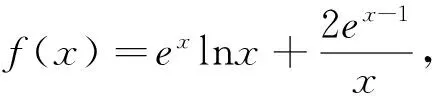
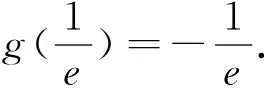
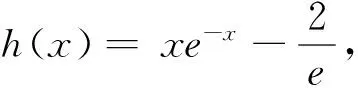
综上,当x>0时,g(x)>h(x),即f(x)>1.
四、重组后的分离函数
对一些问题,表面看两个函数已明显地分离开来了,但分别独立研究却难达目的,此时,我们对问题中的函数重组后分离成比较单一的同名复合函数,这对研究更加有利.
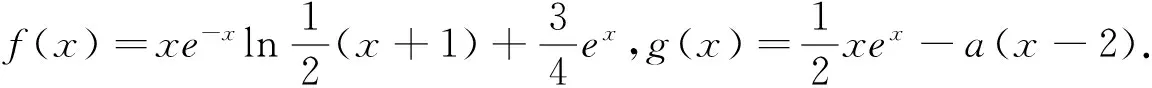
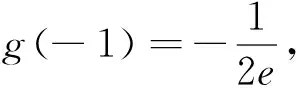
(Ⅱ)若0≤x≤1,f(x) (2)s′(x)=xe2x-e2x-axex+aex=ex(x-1)(ex-a).∵x∈[0,1],∴x-1≤0,ex∈[1,e]. ②若1 研究含参数的问题,分离参数是常法.分离参数后的函数也可以再通过分离函数去求解.这种方法也可称为双分离法. v′(x)=e3x-2e2x-ex+2=(e2x-1)(ex-2),当x<0,x>ln2时,v′(x)>0, ∴v(x)在(ln2,ln3)上为增函数,在(0,ln2)上为减函数. 分离函数法,较适合不同类超越函数基本性质的研究.理论上讲,若分离后的两类函数在一定范围内的上确界、下确界存在明显的分界点,用分离这两类函数分别运算求解,常能奏效.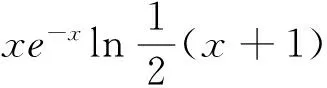
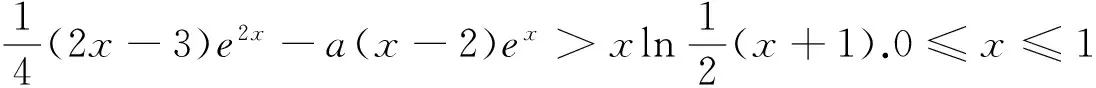
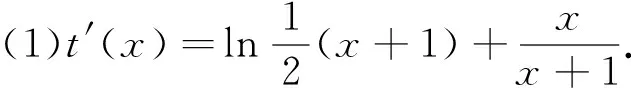
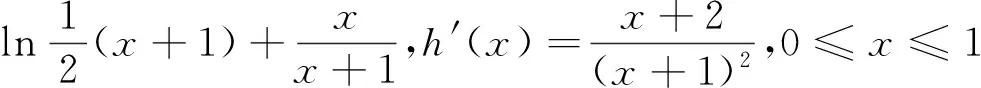
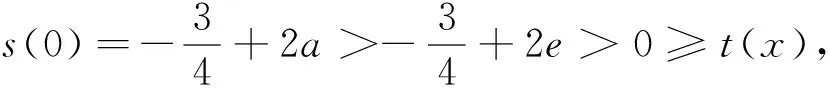
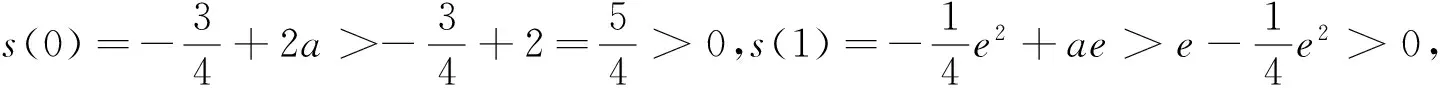
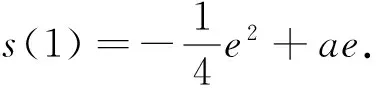
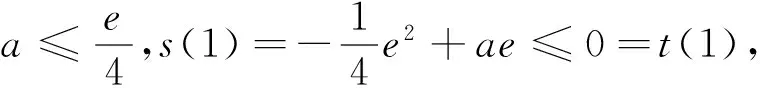
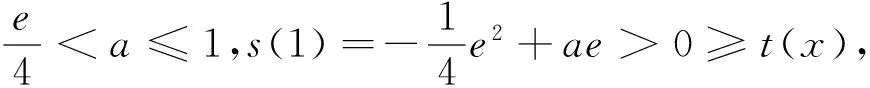
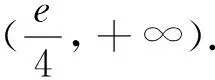
五、分离参数后的分离函数