粘性Cahn-Hilliard方程的半线性Crank-Nicolson格式
李 娟
(南京审计大学 金审学院 基础部, 江苏 南京 210023)
ut-αuxxt+βuxxxx-(u3-u)xx=0,
x∈Ω, t>0,
(1)
边界条件
u(x,t)=uxx(x,t)=0,
x∈∂Ω, t>0,
(2)
初值条件
u(x,0)=u0(x), x∈Ω,
(3)
其中,Ω为有界区间,α≥0,β>0,u表示两相流的浓度,u3-u是内部固有化学势,β为界面能量参数,α表示粘性系数.当α=0时,方程(1)为标准Cahn-Hilliard方程.本文考虑α>0的情形.
在研究玻璃和聚合物两相分离的连续模型中,将分子间的摩擦力考虑进来,提出了粘性Cahn-Hilliard方程.作为重要且应用更广泛的相场模型方程,学者已对其有了广泛的研究.文献[1]指出文献[2]忽略了反映粘性影响的项αuxxt,提出了粘性Cahn-Hilliard方程;文献[3]指出粘性Cahn-Hilliard可被看做相变的奇异极限;文献[4]研究了该方程的亚稳内部层动态;文献[5]对1、2、3维粘性Cahn-Hilliard方程进行了理论分析;文献[6]建立了该方程稳态解的Morse分解和全局吸引子的结构;文献[7]讨论了带有时间周期势的粘性Cahn-Hilliard方程的解的存在性、唯一性和渐进性;文献[8]给出了基于边界条件的最优控制,并证明了方程最优控制解的存在性;文献[9]研究了方程中通道对小参数的限制;文献[10]研究了带有动态边界条件和双障碍源的粘性Cahn-Hilliard方程的最优控制问题;文献[11]研究了非标准的粘性Cahn-Hilliard方程系统解的适定性和长时间行为;文献[12-13]讨论了黏性Cahn-Hilliard方程弱解的存在性.
2 差分格式的建立

下面对问题(1)~(3)建立差分格式.令v=u2ux,则方程(1)等价于
ut-αuxxt+βuxxxx+uxx-3vx=0,
x∈[0,L], t>0,
(4)
v=u2ux, x∈[0,L], t>0.
(5)
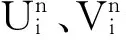

(6)
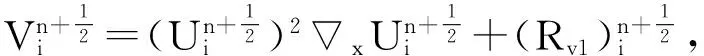
(7)
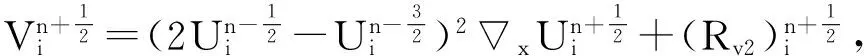
(8)
其中
为截断误差.将(7)和(8)式分别代入(6)式可得

(9)
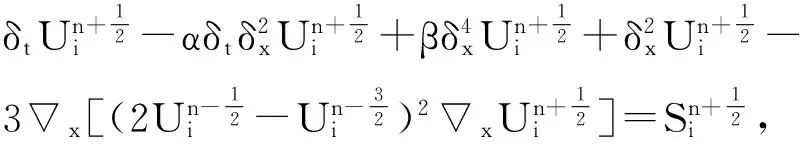
(10)
其中
假定问题(1)~(3)的解是适当光滑的,则存在正常数c0,使得

(11)
由边界条件和初值条件可得
(12)
(13)

(14)
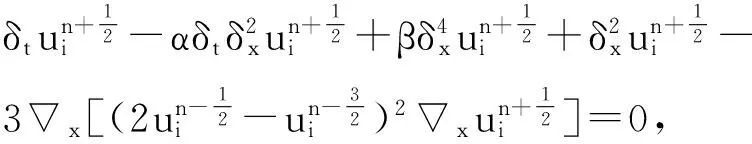
(15)
(16)
(17)
在上面差分格式中,可利用(14)式求得第一、二时间层的数值解.由于其为非线性方程组,故需迭代求解.当un、un-1、un-2(n≥2)为已知时,(15)式为关于un+1的线性方程组,可通过解线性方程组求得其余时间层的数值解.
3 差分格式解的先验估计
下面将给出差分格式解的先验估计式.设Vh={u=(u0,u1,…,uM),u0=uM=0}.对任意的u,v∈Vh,引入如下内积和范数:

为便于先验估计式的推导,引入如下引理.
引理3.1[20]对任意的u,v∈Vh,存在
(u,δxv)=-(δxu,v), (u,xv)=-(xu,v),
‖xu‖≤‖δxu‖.
引理3.2[21]对任意的v∈Vh和p≥2,存在
‖v‖p≤μ(‖v‖1-γ‖δxv‖γ+‖v‖),
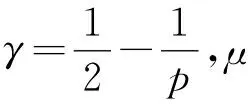
下面,对于差分格式的数值解un,给出‖un‖,‖δxun‖的先验估计式,进一步得出‖un‖∞的有界性.

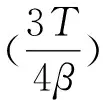
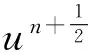

(18)
利用引理3.1可得
(19)
由内积定义知
(20)
由引理3.1和柯西不等式可得
(21)
将(20)和(21)式代入(19)式可得

(22)
记
Fn=‖un‖2+α‖δxun‖2.
由(22)式可得
(23)
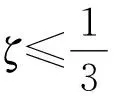
(24)
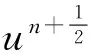

(25)
从而有
(26)
(27)
结合(24)和(27)式可知,对于0≤n≤N-1,(27)式均成立.
由离散的Gronwall不等式可得
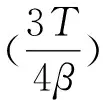
从而有
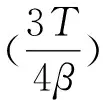
(28)

(29)
根据上面定理,易证差分格式的解是有界的.在引理3.2中,取p=∞有
(30)
由定理3.1中的估计式(28)~(30)可得,存在不依赖于h、τ的正常数B,使得
‖un‖∞≤B, 0≤n≤N,
(31)
即差分格式的解是有界的.
4 差分格式的收敛性
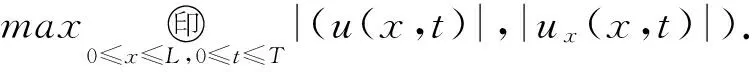
(32)
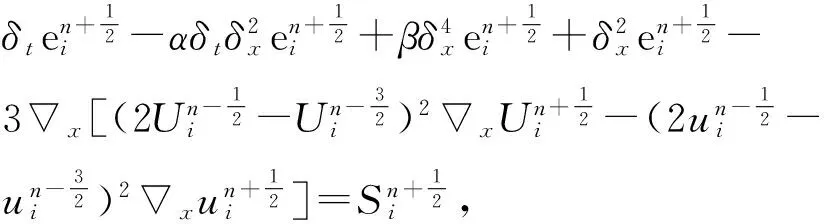
(33)
(34)
(35)
定理4.1假设问题(1)~(3)的解适当光滑.差分格式(14)~(17)式的解收敛于问题的精确解,收敛阶为时间、空间方向二阶收敛,即存在正常数c,使得
‖en‖∞≤c(τ2+h2), 0≤n≤N.
(36)
证明采用数学归纳法证明定理成立.由(35)式知,当n=0时,(36)式成立.
I) 当n=1,2时,‖en‖∞≤c(τ2+h2)成立.

(37)
由引理3.1可得
(38)
下面估计(38)式右端的第二项和第三项.对于第二项有
(39)
从而有
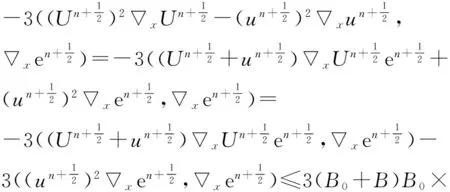
(40)
对于第三项有
(41)
将(40)和(41)式代入(38)式,可得
(42)
由引理3.1和柯西不等式可得
将上式代入(42)式可得
(43)
令En=‖en‖2+α‖δxen‖2.由(43)式可得
其中
从而有
(44)
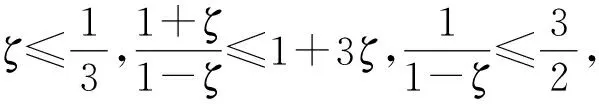
由(44)式可得

从而有
(45)

(46)
由引理3.2可得
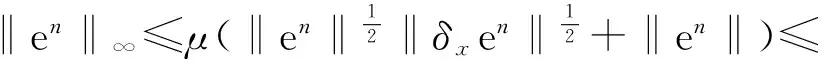
即当n=1,2时,(36)式成立.
(II) 假设定理结论对0≤n≤m均成立,证明‖em+1‖≤c(τ2+h2)成立.

(47)
从而有
(48)
下面估计上式右端的第二、三项.对于第二项有
及
成立,从而有
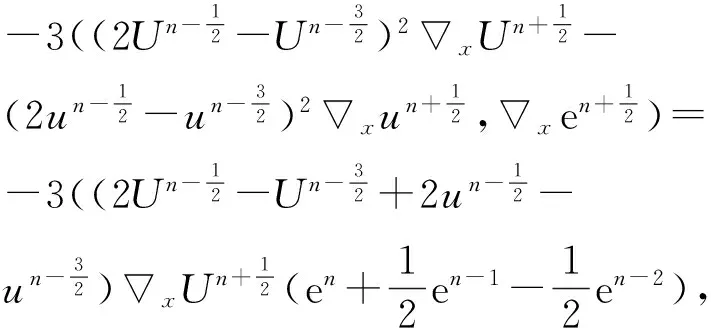
(49)
对于第三项有
(50)
将(49)和(50)式代入(48)式可得
(51)
注意到
并将其代入到(51)式可得
(52)
其中
在(52)式中,用l代替n,并对l从2到n求和可得
从而有
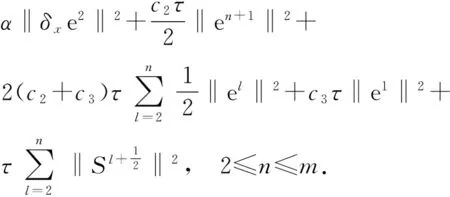
(53)

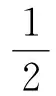
(54)
其中

令
由(53)式可得
由离散的Gronwall不等式可得
En+1≤c4exp(c5T)(τ2+h2)2, 2≤n≤m,
从而有
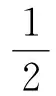
应用引理3.2可得
即当n=m+1时,(36)式成立.由数学归纳法,定理结论成立.
5 数值算例

1) 验证差分格式的精度.由于无法计算该问题的精确解,为验证数值收敛阶,定义如下最大模误差

对于充分小的空间步长h,定义时间收敛阶
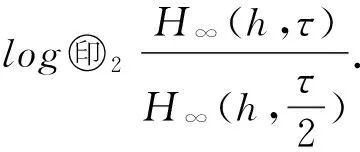
对于充分小的时间步长τ,定义空间收敛阶
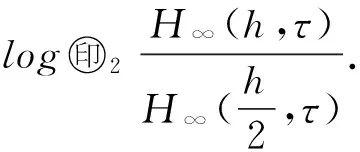

表 1 差分格式(14)~(17)的最大模误差和时间收敛阶
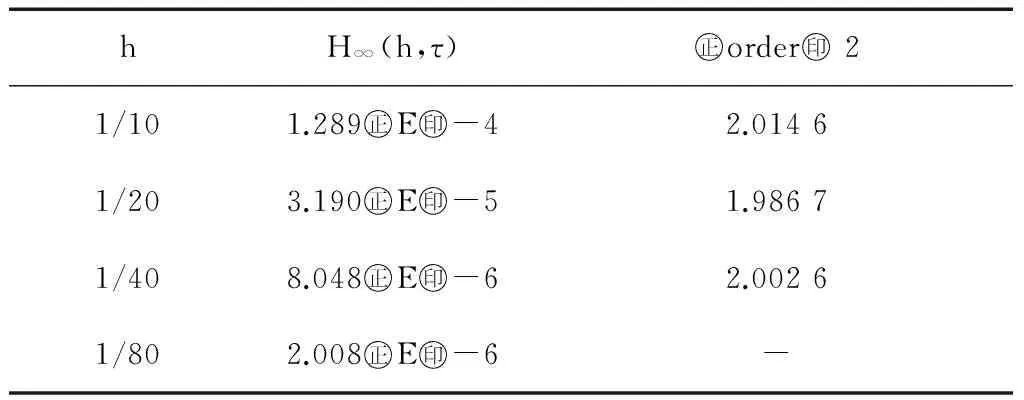
表 2 差分格式(14)~(17)的最大模误差和空间收敛阶
6 小结

图 1 当β=0.5,α=0.5,0.05,0.005,0时,(1)~(3)式的数值解曲面
[1] NOVICK-COHEN A. On the viscous Cahn-Hilliard equation[C]//Material Instabilities in Continuum and Related Mathematical Problems. Oxford:Oxford Univ Press,1988.
[2] CAHN J W, HILLIARD J E. Free energy of a non-uniform system I. interface free energy[J]. J Chem Phys,1958,28(2):258-267.
[3] BAI F, ELLIOTT C M, GARDINER A, et al. The viscous Cahn-Hilliard equation. part I:computations[J]. Nonlinearity,1995,8(2):131-160.
[4] REYNA L G, WARD M J. Metastable internal layer dynamics for the viscous Cahn-Hilliard equation[J]. Methods Appl Anal,1995,2(3):285-306.
[5] ELLIOTT C M. Viscous Cahn-Hilliard equation II. analysis[J]. J Diff Eqns,1996,128(2):387-414.
[6] GRINFELD M, NOVICK-COHEN A. The viscous Cahn-Hilliard equation:morse decomposition and structure of the global attractor[J]. Trans Am Math Soc,1999,351(6):2375-2406.
[7] LI Y, YIN J. The viscous Cahn-Hilliard equation with periodic potentials and sources[J]. J Fixed Point Theory Appl,2011,9(1):63-84.
[8] ZHAO X, LIU C. Optimal control problem for viscous Cahn-Hilliard equation[J]. Nonlinear Analysis,2011,74(17):6348-6357.
[9] THANH B L T, SMARRAZZO F, TESEI A. Passage to the limit over small parameters in the viscous Cahn-Hilliard equation[J]. J Math Anal Appl,2014,420(2):1265-1300.
[10] COLLI P, FARSHBAF-SHAKERM H, GILARDI G, et al. Optimal boundary control of a viscous Cahn-Hilliard system with dynamic boundary condition and double obstacle potentials[J]. SIAM J Control Optim,2015,53(4):2696-2721.
[11] COLLI P, GILARDI G, PODIO-GUIDUGLI P, et al. Well-posedness and long-time behavior for a nonstandard viscous Cahn-Hilliard system[J]. SIAM J Appl Math,2011,71:1849-1870.
[12] 喻朝阳. 黏性Cahn-Hilliard方程弱解的存在唯一性[J]. 四川师范大学学报(自然科学版),2012,35(2):227-230.
[13] 姜金平,董超雨. 粘性Cahn-Hilliard方程在H1中的弱解存在性[J]. 贵州大学学报(自然科学版),2015,32(6):1-3.
[14] MOHYUD-DIN S T, YLDRM A, SARAYDN S. Approximate series solutions of the viscous Cahn-Hilliard equation via the homotopy perturbation method[J]. World Appl Sci,2010,11:813-818.
[15] CHOO S M, CHUNG S K, LEE Y J. A conservative difference scheme for the viscous Cahn-Hilliard equation with a nonconstant gradient energy coefficient[J]. Appl Numer Math,2004,51(2):207-219.
[16] CHOO S M, KIM Y H. Finite element scheme for the viscous Cahn-Hilliard equation with a nonconstant gradient energy coefficient[J]. Appl Math Comput,2005,19(1):385-395.
[17] MOMANI S, ERTURK V S. A numerical scheme for the solution of viscous Cahn-Hilliard equation[J]. Numer Methods Partial Diff Eqns,2008,24(2):663-669.
[18] SHIN J, CHOI Y, KIM J. An unconditional stable numerical method for the viscous Cahn-Hilliard equation[J]. Discrete Contin Dyn Sys,2014,B19(6):1737-1747.
[19] CHOO S M, CHUNG S K. A conservative nonlinear difference scheme for the viscous Cahn-Hilliard equation[J]. Appl Math Comput,2004,16(1):53-68.
[20] 孙志忠. 偏微分方程数值解法[M]. 2版. 北京:科学出版社,2012.
[21] ZHOU Y. Applications of Discrete Functional Analysis of Finite Difference Method[M]. New York:International Academic Publishers,1990.
[22] LI J, SUN Z Z, ZHAO X. A three level linearized compact difference scheme for the Cahn-Hilliard equation[J]. Sci China Math,2012,55(4):805-826.
[23] 李娟,高广花. 求解Fisher-Kolomogorov方程的三层线性化紧差分格式[J]. 西南民族大学学报(自然科学版),2015,41(5):634-639.
[24] 李娟,高广花. 二维扩展Fisher-Kolmogorov方程的线性化紧差分格式的最大模误差分析[J]. 西南师范大学学报(自然科学版),2017,42(3):12-21.

