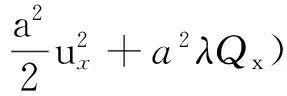具有强迫的Dullin-Gottwald-Holm方程整体弱解的唯一性

李 彬, 朱世辉, 冷礼辉

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 西华大学 理学院, 四川 成都 610039)

本文主要研究如下具有强迫项的DGH方程

ut-a2utxx+kux+3uux+γuxxx-

a2(2uxuxx+uuxxx)-λu=0,

(1)

u(0,x)=u0(x),

(2)

经典的不带强迫项的DGH方程是由Dullin[4]提出;文献[5]在Hs,s≥3/2中,利用Kato半群理论得到了经典DGH方程强解的局部适定性,并讨论了一些波爆破的充分条件;进一步地,文献[6]在Hs,s≥3/2中,利用经典DGH方程的双哈密顿结构和Kato理论,证明了Cauchy问题(1)和(2)整体解的存在性及爆破现象.关于经典的DGH方程爆破解的研究成果较多,可参见文献[2,5,7-10].最近,文献[11]利用特征线法和平衡律,得到了当u0∈H1(R)时,C-H方程整体弱解的唯一性,本文将在此基础上对方程(1)整体弱解的唯一性进行探究.

注意到:当k=0=γ,a=1以及λ=0时,方程(1)为经典的Camassa-Holm方程.文献[12]使用逆散射方法讨论了CH方程的可积性理论.文献[13]研究了CH方程在Sobolev空间Hs,s>3中强解的局部适定性.文献[14]在空间Hs(R)(s≥3/2)中得出了CH方程解的局部适定性.

文献[15-16]研究了H1中CH方程整体弱解的存在性和唯一性.文献[17-18]利用特征线方法得到CH方程整体弱解的存在性.

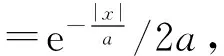
ut+uux+Px+kQx-λQ=0,

(3)

其中奇异积分算子P、Q定义为:

(4)

本文将研究Cauchy问题(3)和(2)的弱解.为进一步探索方程(3)的结构,不妨设u为方程(3)的光滑解.对方程(3)关于x求偏导数,并两端同时乘以2ux,可得

k(Q-u)-a2λQx)=0.

(5)

由于(5)式的第3项仅仅只含有ux,因此把(5)式叫做平衡律(尽管其中也涉及到一些非线性项[17].此平衡律在研究经典的CH方程整体弱解的存在性中起到关键作用[17-18].尽管DGH方程(3)满足平衡律(5),由于强迫项的作用,DGH方程(3)不满足能量守恒律,即

其中C为常数,且在方程(3)出现了新的奇异算子Q.由文献[11]知道柯西问题(3)和(2)存在整体弱解,自然而然,需要考虑该解的唯一性如何?为此,将利用文献[11]的结果和特征线法克服上述问题.本文的主要结果如下:

定理1设k,λ,a∈R,当函数u0∈H1(R)且关于x为绝对连续时,柯西问题(3)和(2)存在唯一的整体弱解,满足

k(Q-u)-a2λQx)θ}dxdt+

(7)

其中Γ={(t,x)|t,x∈R},且有如下性质成立:

(i) 在t的任意有界区域内,u(t,x)是关于t和x的1/2-Hölder连续的.

(ii) 在L2范数意义下,对于任意的t,映射t→u(t,x)是Lipchitz连续的.

k(Q-u)-a2λQx)θ}dxdt-

(8)

(iv) 当n→+∞时,‖u0,n-u0‖H1→0.相应地,当(t,x)在一个有界区域内时,un(t,x)一致收敛到u(t,x).

1 特征变换

本文首先回顾(3)和(2)式整体弱解的存在性.引入一个新的坐标(t,ξ),定义如下:

(t,y)→(t,ξ),

(9)

方程(3)的特征方程为

y(0,ξ)=y′(ξ).

(10)

对任意的(t,y)∈R×R,ξ=ξ(t,y)有ξt+uξy=0.

定义新的变量

(11)

利用三角不等式的相关性质有

(12)

进而,可求得方程(3)在新的坐标系(t,ξ)以及新的变量(u,v,w)下的表达式.由方程(3)可得

由方程(3),并运用q的性质(ii),可得

对方程(5)关于t求积分可得

[u(1+a2u2x)]xdx,

运用方程(3),并对上式关于ξ求偏导数可得

由此将方程(3)转化为

(13)

与此同时,给出u、v、w在新坐标系下的初值:

w(0,ξ)=1,u(0,ξ)=u′(y′(ξ)),

(14)

其中,u(t,ξ)=u(t,y(t,ξ)),P(t,ξ)=P(t,y(t,ξ)),Px(t,ξ)=Px(t,y(t,ξ)),Q(t,ξ)=Q(t,y(t,ξ)),Qx(t,ξ)=Qx(t,y(t,ξ)),以及P、Q、Px、Qx在新坐标系下的形式为

假设y(t,ξ′)=x,则

因而P、Q、Px、Qx形式可变为

(15)

(16)

(17)

(18)

其中,需要注意到等价的半线性方程组(13)右端项关于v做2π的平移,方程保持不变的.因此,在这里仅假设v∈[-π,π]进行证明即可.由文献[11],运用压缩映射理论和一些新的估计,可得到ODE方程组(13)和(14)局部解的存在性;且该局部解可以延拓为一个整体解;进一步地得出原方程整体弱解的存在性,同时该整体弱解满足弱形式(7)和(8).

2 方程整体弱解的唯一性

本章将在t≥0的条件下,讨论(3)和(2)式整体弱解的唯一性,进而完成定理1的证明(当t<0时,可类似得出).

x(t,η)-μ(t){(-∞,x)}≤η≤

x(t,η)+μ(t){(-∞,x]}.

(19)

x(t,η)+μ(t){(-∞,x(t,η))}.

(20)

下面考虑x、u是否为Lipchitz连续函数,为此引入下述命题:

命题2.1设u=u(t,x)是方程(3)的弱解且满足(8)式.对于任意的t≥0有:

(i)η→x(t,η)和η→u(t,η):=u(t,x(t,η)),由(20)式可知(19)式所定义的形式依然保持着Lipchitz连续(伴随Lipchitz常数1).

(ii)t→x(t,η)是Lipchitz连续的,且Lipchitz常数依赖于‖u0‖H1.

证明(i) 由(20)式中定义的η可得,对任意的t≥0,x→η(t,x)都是右连续且严格递增的,且其逆映射η→x(t,η)是一个好的定义,并且也是连续和递增的.对于任意的η1<η2有

η2-η1=x(t,η2)-x(t,η1)+

x(t,η2)-x(t,η1)+

μ(t){(x(t,η1),x(t,η2)},

(21)

且x(t,η2)-x(t,η1)≤η2-η1,映射η→x(t,η)是Lipchitz连续的(伴随Lipchitz常数1).一方面,对于η→u(t,η),

当η1<η2时,

a|u(t,x(t,η2))-u(t,x(t,η1))|≤

μ(t){(x(t,η1),x(t,η2))}.

另一方面,由(21)式可知η→u(t,η)是Lipchitz连续的(且Lipchitz常数1/2<1).

‖u2‖L2+a2‖λQx‖L2)≤C0,

其中C0仅仅依赖于‖u‖H1.对任意的t>τ,由(8)式可得

μ(t){(-∞,y-C∞(t-τ))}≤

μ(τ){(-∞,y)}+

μ(τ){(-∞,y)}+C0(t-τ).

设y-(t)=y-(C∞+C0)(t-τ),则有

y-(t)+μ(t){(-∞,y-(t))}≤

y-(C∞+C0)(t-τ)+

μ(t){(-∞,y)}+C0(t-τ)≤

τy-μ(τ){(-∞,y)}≤η.

进而对任意的t>τ有x(t,η)≥y-(t),同理可得

x(t,η)≤y+(t):=y+(C∞+C0)(t-τ).

从而映射t→x(t,η)为一致Lipchitz连续.

第二步:如下命题表明:特征线可以由一个积分方程唯一确定,而结合特征方程和平衡律可以唯一确定一个积分方程,因此它是研究方程(3)保守解的唯一性的关键.

命题2.2设u=u(t,x)是方程(3)的弱解且满足(8)式,对任意的x0∈R,存在一个一致Lipchitz连续映射t→x(t),使得对所有的t≥0,有

(22)

以及

x(0)=x0,

(23)

且对任意的0≤τ≤t有

u(t,x(t))-u(τ,x(τ))=

(24)

证明首先,选取适当的点(t,η(·))和以x0为初值的特征线t→x(t)=x(t,η(t)),其中η(·)为一待定映射.将(22)和(23)式相加,并对其关于t积分得

(25)

其中

对任意的t≥0,由x→u(t,x),x→P(t,x)和x→Qx(t,x)皆属于H1(R)可知:(26)式所定义的函数η→J(t,η)为一致有界且绝对连续,且

Jη=[ux+2(u2-P-k(Q-u)+

对任意的τ≥0,若‖η-η0‖=δ>0,那么|η1(τ)-η2(τ)|≤δe2Cτ.由J为Lipchitz连续可得

|[θη1](t)-[θη2](t)|≤

进而映射[θη]是严格压缩的,运用压缩映射原理可知:存在唯一的不动点.进而(26)式有唯一的解:t→η(t),相应的函数t→x(t,η(t))满足(22)和(23)式.再由(25)式可以确定(22)式的一条满足Lipchitz连续的特征线x(t).从而映射t→x(t):=x(t,η(t))是Lipchitz连续函数,且为(25)式提供了唯一解,该唯一解由2个Lipchitz连续函数构成.为了证明这个解满足(22)式,需要说明:对任意的τ>0,(22)式保持如下性质:

(i)x(·)对t=τ是可求导的;

(ii) 测试函数μ(τ)是绝对连续的.

其中ε0>0(当ε0<0时可以做相似的处理).为了导出矛盾,可以看到:对任意的t∈(τ,τ+δ],以及足够小的δ>0有

x+(t):=x(τ)+

(t-τ)[u(τ,x(τ))+ε0]

(27)

同时,如果函数θ的紧支集满足Lipchitz连续,则(8)式还是成立.对任意小的>0,

L

设ϑ(s,y):=min{L(s,y),P(s)},并将其运用到(8)式有

k(Q-u)+a2λQx)uxϑ]dxdt=0.

(29)

当s∈[τ+,t-],以及u为Hölder连续时,有ϑ和u(s,x)

即当t→τ时,

且这族测量函数μ(t)关于t的连续依赖性在弱拓扑下是否依测度收敛.当→0时,有τ,t∉T,则

k(Q-u)+a2λQx)uxdxds+o1(t-τ), (30)

k(Q-u)+a2λQx)ux)dxds|≤

一方面,将(27)和(30)式代入到η(t)里,断言:对任意的τ

η(t)>x(τ)+(t-τ)[u(τ,x(τ))+ε0]+

k(Q-u))dxds+o1(t-τ).

(31)

另一方面,由(25)和(26)式可知

η(t)=η(τ)+(t-τ)[u(τ,x(τ))+

(32)

其中

x(τ)+(t-τ)[u(τ,x(τ))+ε0]+

化简可得:当t→τ时,有ε0≤0,这与条件矛盾.

ϑt+uuxϑx-(u2-P-k(Q-u)+

(33)

同理,在(33)式中对任意测试函数ϑ,其紧支集都是Lipchitz连续.对任意小的>0,考虑函数

进一步,定义ψ(s,y):=min{(s,y),P(s)},其中P(s)为(28)式所定义的形式.取ϑ=ψ,并让→0.由(-Px-kQx+λQ)连续性可得

(34)

对任意的s∈[τ-,t+],

x(s)

即

进而

(35)

由(34)和(35)式得(24)式是成立的.

最后,证明x(t)的唯一性.假设存在2个不同的x1(t)和x2(t),且都满足(22)和(23)式;选择适当的可测函数η1和η2使得x1(t)=x(t,η1(t))和x2(t)=x(t,η2(t));在相同初值x(0)=x0下,η1(·)和η2(·)满足(25)式,但这与η的唯一性矛盾.

第三步:下面对η和u赋予一些重要的性质.

命题2.3如果u=u(t,x)为方程(3)的一个弱解且满足(8)式,那么

(i) 映射(t,η)→u(t,η):=u(t,x(t,η))为Lipchitz连续函数,且Lipchitz常数仅仅依赖于‖u0‖H1;

(ii) 设t→η(t;τ,η0)是积分方程(25)式的解,且满足

(36)

断言:存在一个常数C,使得对于任意的η1,0,η2,0,t,τ≥0,其相应的解都满足

|η(t;τ,η1,0)-η(t;τ,η2,0)|≤

eC|t-τ||eta1,0-η2,0|.

(37)

证明(i) 由(20)、(24)和(25)式可得

|u(t,x(t,η0))-u(τ,η0)|≤

|u(t,x(t,η0))-u(t,x(t,η(t)))|+

|u(t,x(t,η(t)))-u(τ,x(τ,η(τ)))|≤

kQx+λQ‖L∞≤C(t-τ),

其中

k‖Qx‖L∞+‖λQ‖L∞>0

仅仅依赖于‖u0‖H1.

(ii) 由J为Lipchitz连续函数可知

|η(t;τ,η1,0)-η(t;τ,η2,0)|≤|η1,0-η2,0|+

利用Gronwall不等式可以得到(37)式.

第四步:给出定理1.2的证明.

证明首先,由命题2.1和命题2.3可知:映射(t,η)→(x,u)(t,η)为Lipchitz连续函数.同理可得:映射η→J(t,η):=J(t,x(t,η))和η→P(t,η):=P(t,x(t,η)),η→Px(t,η):=Px(t,x(t,η)),η→Q(t,η):=Q(t,x(t,η))和η→Qx(t,η):=Qx(t,x(t,η))也是Lipchitz连续函数的.由Rademacher定理[21]可知:偏导数xt、xη、ut、uη、Jη、Pη、Qη、(Px)η和(Qx)η几乎处处存在,且点(t,η)关于这些偏导数都是勒贝格点.称t→η(t,η0)是积分方程(25)式的唯一解.由命题2.2可知:对几乎所有的η0有

(JC) 对所有的t>0,点(t,η(t,η0))关于所有的偏导数xt、xη、ut、uη、Jη、Pη、Qη、(Px)η和(Qx)η都为勒贝格点.而且对所有的t>0有xη(t,η(t,η0))>0.

如果(JC)保持上述性质,那么就说t→η(t,η0)有一个很好的特性.进一步地,寻求这样的一个常微分方程:有一个很好的特性来描述的数量uη和xη.如命题2.3所示,记t→W(t):=η(t;τ,η0)为方程(36)式的解.如果τ,t∉T,假设W(t)有一个好的性质,且对η0是可微的,那么

其次,对

关于η0求偏导:

(39)

同理,对(24)式关于η0求偏导有

利用(38)～(40)式得

特别地,在(41)式方括号内的左边的函数是绝对连续的.因为

根据(41)式可得

其中第一个方程是由(41)式的前2个方程得到,第二个方程是由(40)式第一个和第三次方程得到.

第二,回到起始坐标(t,x),且ux的一条好的特征曲线.对于任意的(τ,x0),τ∉T,设映射x→ux(τ,x)的初值x0为勒贝格点,让η0满足:x0=x(τ,η0),并且t→W(t)有一个很好的性质,使得(JC)保持相应的性质.当xη>0时,有

即如果xη(τ,η0)>0,且这条特征线经过点(τ,x0),那么偏导数ux可进行如下计算:

利用(39)和(40)式有:当xη≠0时,映射t→ux(t,x(t,W(t)))是绝对连续的,且满足(在计算时,注意乘以

(43)

引入函数v

有

(44)

下面,v将被视为一个定义在单位圆内的映射S:=[-π,π].表明,存在一条恰当的特征线,使得映射t→v(t):=v(t,x(t,η(t;τ,η0)))是绝对连续的,且满足

(45)

第三,设u=u(t,x)为方程(3)的整体弱解且满足(8)式.如先前分析:t、η、x、u、v满足半线性系统

重述(4)及(26)式中所定义的P、Q和J,且函数P、Px、Q和Qx满足上述η的条件.

以及相应的初值:对任意的η0∈R,

其中所有系数都是Lipchitz连续的,则对任意的t≥0,x∈R,初值问题(46)和(47)有整体唯一解.

u(t,x)=u(t,η*(t,x))=

[1]ZHUSH.ExistenceanduniquenessofglobalweaksolutionsoftheCamassa-Holmequationwithaforcing[J].DiscreteContinuousDynamicalSystems,2016,A36(9):5201-5221.

[2]CONSTANTINA,LANNESD.ThehydrodynamicalrelevanceoftheCamassa-HolmandDegasperis-Procesiequations[J].ArchiveforRationalMechanicsAnalysis,2009,192(1):165.

[3]KRISHNANEV,KHANQJA.LiegroupoftransformationsforaKdV-Boussinesqequation[J].CzechoslovakJournalofPhysics,2003,53(2):99-105.

[4]DULLINHR,GOTTWALDGA,HOLMDD.Anintegrableshallowwaterequationwithlinearandnonlineardispersion[J].PhysicalReviewLetters,2001,87(19):194501.

[5]LIUY.Globalexistenceandblow-upsolutionsforanonlinearshallowwaterequation[J].MathAnn,2006,335(3):717-735.

[6]TIANL,GUIG,LIUY.Onthewell-posednessproblemandthescatteringproblemfortheDullin-Gottwald-Holmequation[J].CommunicationsinMathematicalPhysics,2005,257(3):667-701.

[7]NOVRUZOVE.Blow-upofsolutionsforthedissipativeDullin-Gottwald-Holmequationwitharbitrarycoefficients[J].JournalofDifferentialEquations,2016,261(2):1115-1127.

[8]ZHOUY.Blow-upofsolutionstotheDGHequation[J].JFunctAnal,2007,250(1):227-248.

[9]ZHOUY,GUOZ.BlowupandpropagationspeedofsolutionstotheDGHequation[J].DiscreteandContinuousDynamicalSystems,2012,B12(3):657-670.

[10]YINZ.Globalexistenceandblow-upforaperiodicintegrableshallowwaterequationwithlinearandnonlineardispersion[J].DynamicsofContinuousDiscreteImpulsiveSystems,2005,12(1):129.

[11]LIMJ,ZHANGQT.Uniquenessofconservativesolutionstothetwo-componentCamassa-Holmsystemviacharacteristics[J].CommunMathSci,2016,14(6):1581-1597.

[12]CONSTANTINA,MCKEANHP.Ashallowwaterequationonthecircle[J].CommunPureApplMath,2015,52(8):949-982.

[13]CONSTANTINA,ESCHERJ.Particletrajectoriesinsolitarywaterwaves[J].BullAmMathSoc,2007,44(44):423-431.

[14]YIAL,OLVERPJ.Well-posednessandblow-upsolutionsforanintegrablenonlinearlydispersivemodelwaveequation[J].JournalofDifferentialEquations,2000,162(1):27-63.

[15]XINZP,ZHANGP.Ontheweaksolutiontoashallowwaterequation[J].CommunPureApplMath,2000,53(11):1411-1433.

[16]XINZP,ZHANGP.Ontheuniquenessandlargetimebehavioroftheweaksolutionstoashallowwaterequation[J].CommunicationsinPartialDifferentialEquations,2002,27(9/10):1815-1844.

[17]BRESSANA,CONSTANTINA.GlobalconservativesolutionstotheCamassa-Holmequation[J].AnalysisApplications,2007,183(3):215-239.

[18]BRESSANA,CONSTANTINA.GlobaldisspativesolutionsoftheCamassa-holmequation[J].AnalysisApplications,2007,5(1):1-27.

[19]BRESSANA,CHENG,ZHANGQ.UniquenessofconservativesolutionstotheCamassa-Holmequationviacharacteristics[J].DiscreteContinuousDynamicalSystems,2014,A35(1):25-42.

[20]BRESSANA,CHENG,ZHANGQ.Uniqueconservativesolutionstoavariationalwaveequation[J].ArchiveforRationalMechanicsAnalysis,2015,217(3):1069-1101.

[21]EVANSLC.Partialdifferentialequations[C]//2ndEd.GraduateStudiesinMathematics, 19.ProvidenceRI:AmMathSoc,2010,19(1):211-223.

[22]CHENG,SHENY.Existenceandregularityofsolutionsinnonlinearwaveequations[J].DiscreteContinuousDynamicalSystems,2017,A35(8):3327-3342.