模块化多电平功率变换器建模与控制

武卫强,王立宝,邵文权,程 远

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

由于器件耐压等级与功率等级的限制,传统方式是采用器件的串并联来满足电力电子设备对高压大功率的需求.但是,器件的串并联存在动静态的均压与均流问题,使控制方法变得相当复杂,因此出现了多电平技术.多电平技术通过改变自身拓扑来实现高压大功率输出,具有输出电平数多、电压等级高且可变以及输出波形质量高等优势.2001年,德国学者 Marquardt R与Lesnicar A共同提出MMC拓扑结构.MMC不仅具有多电平技术的优点,还具有其他优势[1],例如交流侧无需滤波装置、输出波形谐波含量小且可扩展性强等.因此,国内外将这一技术应用于工程实践[2],如高压直流输电、新能源并网、高压电机驱动等.但是,MMC自身也存在子模块电容电压不均衡、相间环流等问题.

目前,国内外的研究主要集中于MMC子模块电容电压均衡控制与环流抑制等方面.文献 [3-6]针对MMC子模块电压不均衡问题采取了不同的均压控制措施;文献[7-12]对MMC桥臂环流产生的原因、谐波性质、环流对系统造成的危害及抑制手段等方面作了研究.本文依据MMC单相等值电路建立数学模型,并由此得出子模块电容电压中存在二倍频波动分量,相间环流呈负序性质.为了解决MMC子模块电容电压不均衡问题,设计基于冒泡排序算法的载波移相调制策略.在MATLAB中搭建MMC仿真模型,仿真结果验证了理论分析的正确性与控制策略的有效性.

1 MMC基本拓扑与数学建模

图1(a)为MMC主拓扑结构,三相共六个桥臂,每个桥臂都由n个结构相同的子模块级联而成,每个桥臂串联一个电抗器L0.iuj，idj(j=a,b,c)分别为上下桥臂电流,Ud，Id为直流侧电压与电流.图1(b)为子模块拓扑,VT1，VT2代表IGBT,VD1，VD2为反并联二极管,C为子模块储能电容,Uc子模块电容电压,U为子模块端口电压,A、B端为子模块输出端,用于各子模块相互级联.通过控制VT1，VT2开通与关断使子模块工作于投入与切除状态.

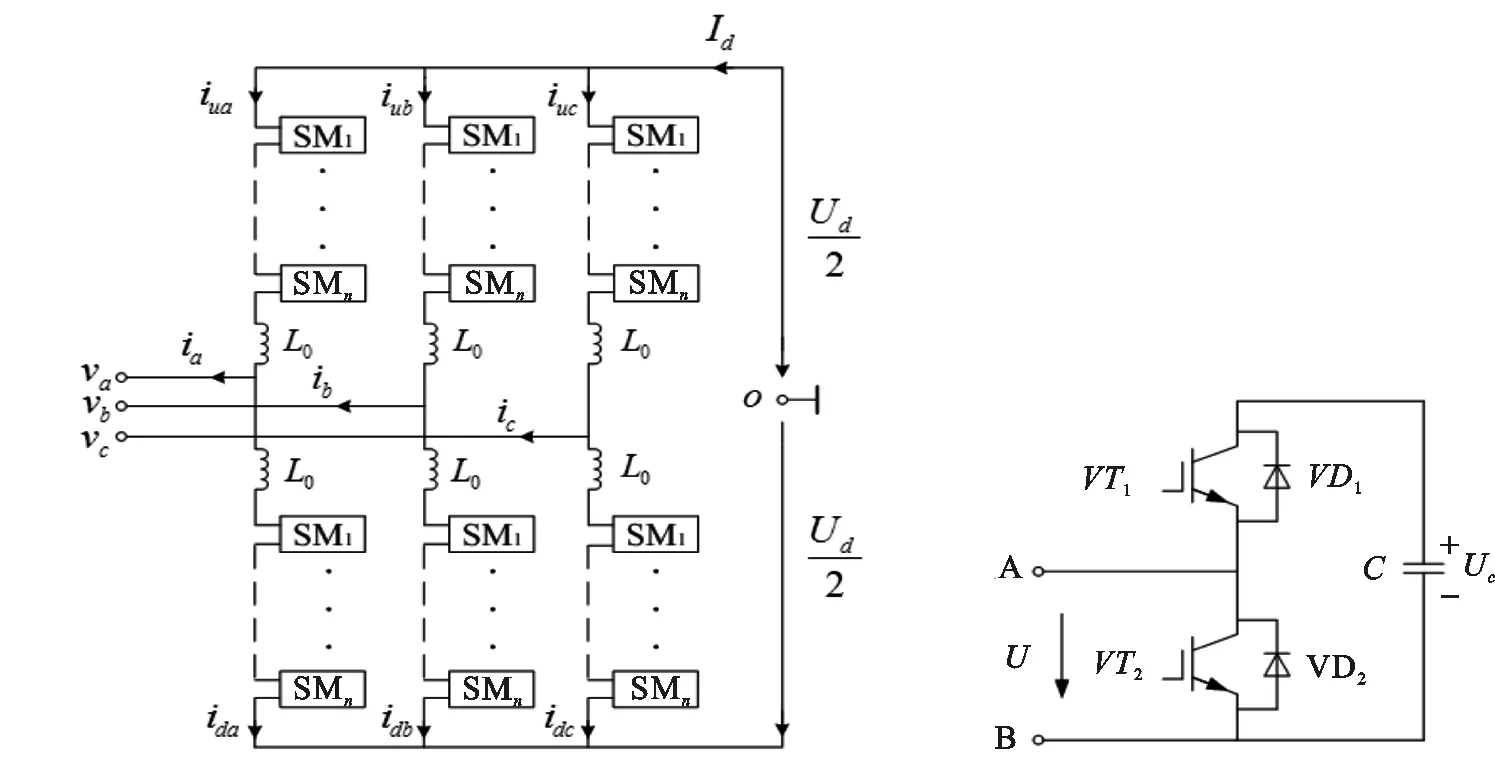
(a) 主拓扑 (b) 子模块拓扑图 1 MMC拓扑Fig.1 MMC topologies

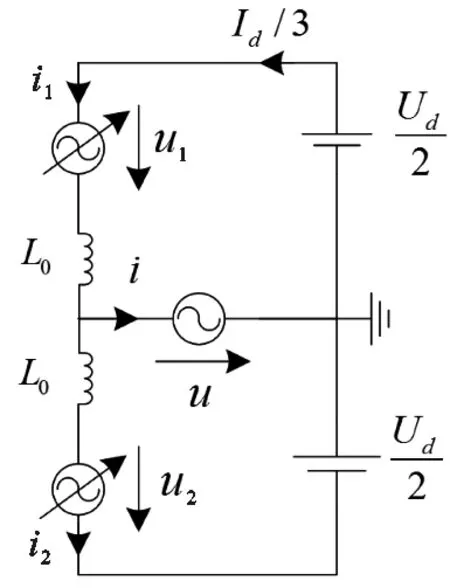
图 2 单相等值电路Fig.2 Single-phase equivalent circuit

依据图1建立MMC单相等值电路模型,如图2所示．将上、下桥臂总电压等效为可控电压源u1和u2.通过该等值电路建立数学模型.首先定义电压调制比k与电流调制比m为[13-14]

(1)

式中，u为交流侧相电压有效值，i为交流侧线电流有效值.以A相为例,对其上下桥臂建立KVL与KCL方程为

(2)

式中：ω0为基波角频率,φ为初相角.

定义上下桥臂开关函数为

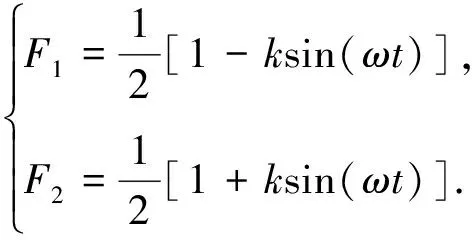
(3)

由式(2)和(3)可得A相上下桥臂子模块电容电压纹波方程为

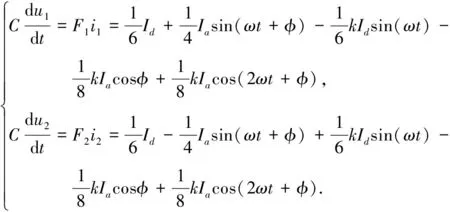
(4)

式：u1,u2分别为上下桥臂子模块电容电压；C是子模块电容值．式(4)表明,MMC运行中,子模块电容电压会出现二倍频波动分量,该二倍频分量会导致MMC相间电压不均衡引起相间二倍频环流,且呈负序性质[9].

2 控制策略

MMC相单元桥臂采用半桥模块串联结构,随着子模块数量的增加,控制难度也相应增大.目前,模块化多电平变换器在小功率场合应用的调制策略[15-18]有载波层叠、载波移相、空间矢量控制.大功率应用场合有特定谐波消去法、空间矢量控制、最近电平逼近控制[19].

为了达到相单元总电压与直流侧电压相同以及子模块电容电压均衡的目的,本文在载波移相脉宽调制方法的基础上应用冒泡排序算法,控制原理如图3所示.对交流侧电压vabc与电流iabc采样,通过3/2“等功率”坐标变换[20]得到交流侧电压和电流有功分量vd，id和无功分量vq，iq,将id,iq分别与其参考值idref，iqref进行比较,所得差值经PI环节输出系统的调制波形,调制波与多个载波相比较得到桥臂所需投入子模块数NU,将NU与子模块电容电压排序编号进行比较,比较结果与输出电流方向共同决定了子模块的投切运行状态.

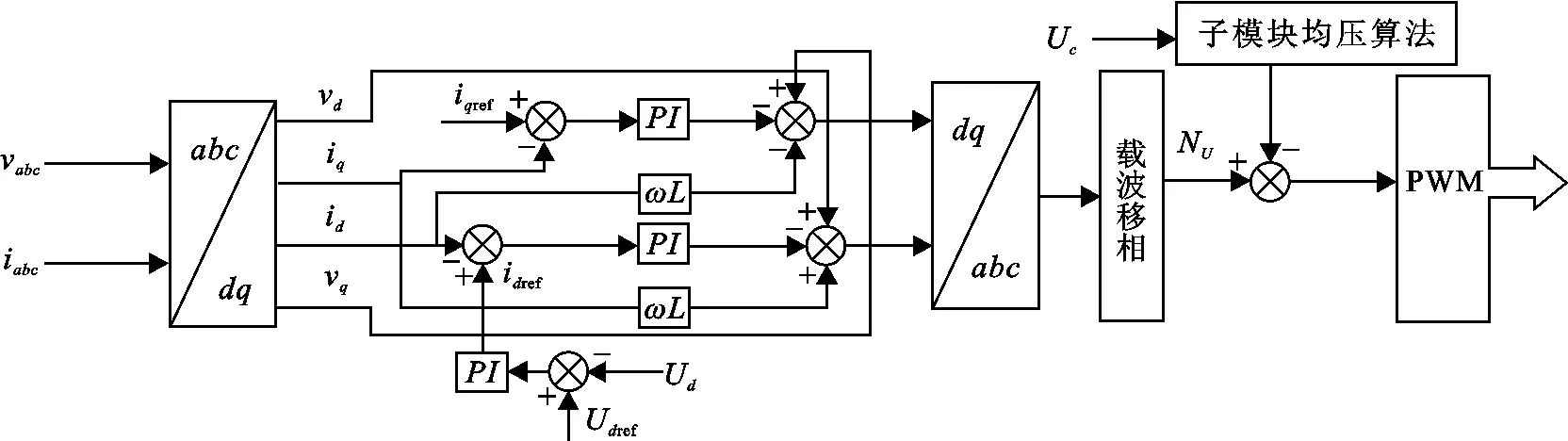
图 3 控制原理Fig.3 Control schematic

子模块电容电压均衡控制分为3步：首先,采集桥臂电流与各子模块电容电压值，按照电容电压大小进行2组排序,一组为升序排序,将其排序结果记为0状态，一组为降序排序,将其排序结果记为1状态;其次,根据桥臂电流流向选择排序状态.当电流方向与参考方向一致,选择0状态,使电容电压较低的子模块优先充电;当电流方向与参考方向相反,选择1状态,电容电压较大的子模块优先放电;最后,将每个子模块电压值在该序列的排序结果记为Index,其中第i个子模块电压值经排序后的编号记为Index(i),将当前桥臂所需投入子模块数NU与Index(i)经过比较环节得到第i个子模块的投切状态.

3 仿真研究

为了验证理论分析与数学建模的正确性,以及调制策略的有效性,本文在MATLAB中搭建了MMC仿真模型.使MMC工作在整流状态,选取桥臂子模块数n=4,相单元子模块电容电压额定值为2.5 kV,子模块电容C0=0.01 F,桥臂电感L0=2 mH,交流侧输入电压为4 kV,所搭模型如图4所示.图4(a)图为MMC主电路,图4(b)为MMC子模块,S1～S6为6个桥臂,每个桥臂都由4个子模块构成.

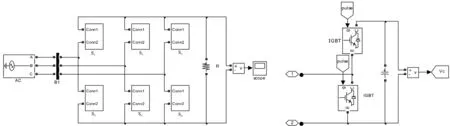
(a) 主电路 (b) 子模块图 4 MMC仿真模型Fig.4 MMC simulation model

图5为MMC整流电路直流侧电压波形.在0～0.08 s内系统达到了稳定状态,直流侧输出电压值稳定在10 kV,稳定后的误差值小于±0.25%,电压实际值能快速、准确跟踪参考值,证明闭环控制策略设计合理.

图 5 直流侧电压图 图 6 A相上桥臂子模块电容电压 Fig.5 DC side voltage Fig.6 A-phase bridge arm sub-module capacitor voltage

图6为A相上桥臂4个子模块电容电压波形.由图6可知,在0～0.5 s内MMC相单元4个子模块电容电压均稳定维持在参考值2 500 V,每个子模块电容电压误差值均小于±4%.证明本文所采用的冒泡排序算法均压效果良好.

MMC在正常工作状态下,由于子模块电容电压存在二倍频电压波动分量,会造成相间二倍频环流问题,图7为MMC相间二倍频环流幅值仿真波形,系统稳定运行状态下,相间二倍频环流幅值为25 A,该二倍频环流在三相桥臂间流动,对外部交流系统不产生影响,环流的存在会造成系统损耗增加.

图 7 相间二倍频环流 图 8 基波与二倍频谐波相位 Fig.7 Circulating current with double frequency Fig.8 Phase of fundamental wave and double harmonic wave

图8为MMC相单元桥臂电流相位关系,图8(a)为三相基波电流相位,图8(b)为三相二倍频环流相位.由图8(a)可知系统稳定后,由上至下A,B,C三相桥臂基波电流互差120°.由图8(b)可知系统在稳定后,由上至下三相环流的相位关系由图8(a)的A,B,C变为图8(b)的A,C,B,且三相之间互差120°.

4 结束语

利用MMC单相等值电路建立其数学模型,由数学模型分析出MMC相间含有二倍频环流且呈负序性质,通过仿真实验验证了理论分析的正确性．针对MMC工作过程中子模块电容电压不均衡现象,设计了基于冒泡排序算法的载波移相调制策略,仿真结果表明本文所设计的控制策略是有效可行的,具有一定的工程实用价值．

参考文献(References)：

[1] MARQUARDT R,LESNICAR A.New concept for high voltage-modular multilevel converter[C]//Proceedings of the 34th IEEE Annual Power Electronics Specialists Conference.Acapulco:IEEE,2003:20-25.

[2] 杨晓峰,郑琼林,薛尧,等.模块化多电平换流器的拓扑和工业应用综述[J].电网技术,2016,40(1):1-10.

YANG X F,ZHENG Q L,XUE Y,et al.Review on topology and industry applications of modular multilevel converter[J].Power System Technology,2016,4(1):1-10.

[3] 陈耀军,陈柏超,袁佳歆,等.模块化多电平逆变器电容电压及环流控制[J].电工技术学报,2014,29(10):166-174.

CHEN Y J,CHEN B C,YUAN J X,et al.The control of capacitor voltages and circulating currents of the modular multilevel inverter[J].Transactions of China Electrotechnical Society,2014,29(10):166-174.

[4] 陈耀军,陈柏超,钟炎平,等.模块化多电平变换器全电平产生原理及电容均压策略[J].电力系统自动化,2015,39(23):126-131.

CHEN Y J,CHEN B C,ZHONG Y P,et al.Study on full level generation and capacitor voltage balance strategy of the modular multilevel converter[J].Automation of Electric Power Systems,2015,39(23):126-131.

[5] 罗永捷,李子欣,李耀华,等.一种模块化多电平换流器分布式均压控制策略[J].电源学报,2015,13(6):77-83.

LUO Y J,LI Z X,LI Y H,et al.A distributed control method for voltage balancing in modular multilevel converters[J].Journal of Power Supply,2015,13(6):77-83.

[6] 郭高朋,姚良忠,温家良.模块化多电平变流器的子模块分组调制及均压控制[J].中国电机工程学报,2016,36(1):145-153.

GAO G P,YAO L Z,WEN J L.The grouping modulation and voltage balance control of the sub-modules in modular multilevel converter[J].Proceedings of the CSEE,2016,36(1):145-153.

[7] 屠卿瑞,徐政,郑翔,等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术,2010,36(2):547-552.

TU Q R,XU Z,ZHENG X,et al.Mechanism analysis on the circulating current in modular multilevel converter based HVDC[J].High Voltage Engineering,2010,36(2):547-552.

[8] 杨晓峰,郑琼林.基于MMC环流模型的通用环流抑制策略[J].中国电机工程学报,2012,32(18):59-65.

YANG X F,ZHENG Q L.A novel universal circulating current suppressing strategy based on the MMC circulating current model[J].Proceedings of the CSEE,2012,32(18):59-65.

[9] 周月宾,江道卓,郭捷,等.模块化多电平换流器子模块电容电压波动与内部环流分析[J].中国电机工程学报,2012,32(24):8-14.

ZHOU Y B,JIANG D Z,GUO J,et al.Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters[J].Proceedings of the CSEE, 2012,32(24):8-14.

[10] 李国庆,辛业春,吴学光.模块化多电平换流器桥臂电流分析及其环流抑制方法[J].电力系统自动化,2014,38(24):62-67.

LI G Q,XIN Y C,WU X G.Arm current analysis of modular multilevel converter and its circulating current suppressing method[J].Automation of Electric Power Systems,2014,38(24):62-67.

[11] 王朝明,王华广,王 晴.基于双 PI 控制器的模块化多电平变换器环流抑制策略[J].电网技术,2014,38(10):2905-2912.

WANG C M,WANG H G,WANG Q.A dual PI controller based strategy to suppress circulating current in modular multilevel converter[J].Power System Technology,2014,38(10):2905-2912.

[12] 班明飞,申科,王建赜,等.基于准比例谐振控制的MMC新型环流抑制器[J].电力系统自动化,2014,38(11):85-89.

BAN M F,SHEN K,WANG J Z,et al.A novel circulating current suppressor for modular multilevel converters based on quasi-propotional-resonant control[J].Automation of Electric Power Systems,2014,38(11):85-89.

[13] 徐政.柔性直流输电系统[M].北京:机械工业出版社,2012:11.

XU Z.Flexible DC transmission system[M].Beijing:Mechanical Industry Press,2012:11.

[14] TU Q,XU Z.Impact of sampling frequency on harmonic distortion for modular multilevel converter[J].IEEE Transactions on Power Delivery，2010,26(1):298-306.

[15] 张建坡,赵成勇.模块化多电平换流器环流及抑制策略研究[J].电工技术学报,2013,28(10):328-336.

ZHANG J P,ZHAO C Y.Research on circulation current and suppressing strategy of modular multilevel converter[J].Transactions of China Electrotechnical Society,2013,28(10):328-336.

[16] 公铮,伍小杰,王钊,等.基于载波移相调制的模块化多电平变换器变频运行控制[J].中国电机工程学报,2015,35(11):2822-2830.

GONG Z,WU X J,WANG Z,et al.Variable frequency operation control of modular multilevel converter based on carrier phase-shift modulation[J].Proceedings of the CSEE,2015,35(11):2822-2830.

[17] 周莹坤,齐磊,崔翔,等.采用载波移相调制的模块化多电平换流器损耗一致性分析[J].电力系统自动化,2016,40(20):100-106.

ZHOU Y K,QI L,CUI X,et al.Loss consistency analysis of modular multilevel converter using carrier phase shifted sinusoidal pulse width modulation [J].Automation of Electric Power Systems,2016,40(20):100-106.

[18] 丁冠军,汤广福,丁明,等.新型多电平电压源型换流器模块的拓扑机制与调制策略[J].中国电机工程学报,2009,29(36):1-8.

DING G J,TANG G F,DING M,et al.Topology mechanism and modulation scheme of a new multilevel voltage source converter modular[J].Proceedings of the CSEE,2009,29(36):1-8.

[19] 申科,王建赜,班明飞,等.基于阶梯波调制的MMC电容电压平衡控制方法对比研究[J].电机与控制学报,2016,20(10):1-8.

SHEN K,WANG J Y,BANG M F,et al.Comparative analysis on capacitor voltage balance control strategies for staircase modulated modular multilevel converter[J].Electric Machines and Control,2016,20(10):1-8.

[20] 程远,孟昭亮,邵文权.风电机组并网整流系统的设计[J].西安工程大学学报,2015,29(5):611-616.

CHEN Y,MENG Z L,SHAO W Q.Design of rectifier system of wind turbines grid[J].Journal of Xi′an Polytechnic University,2015,29(5):611-616.