隧道点云格网化方法分析研究
李开伟 ,陈 刚 ,张云山 ,任 礼
(1.四川水利职业技术学院,四川 成都 610000;2.郑州测绘学校,河南 郑州 450015;3.中交二公局第三工程有限公司,陕西 西安71001)
三维激光扫描仪扫描过程中[1-4],获得了大量密集的点云信息,部分学者利用不同的方法充分挖掘点云信息进行分析和研究,其中点云格网化是常用的方法。如文献[5]利用点云格网化进行迭代曲面拟合滤波,生成DTM;文献[6]将点云格网化应用于点云数据预处理,避免点云数据内插或者平滑造成的信息损失;文献[7]根据点云分布的密度,提出把扫描点云格网化进行信息提取的新方法;文献[8]对点云数据进行格网细化,提高运算效率;文献[9]通过格网化处理削弱偶然误差。这些研究将点云格网化应用于点云数据预处理、点云信息提取等,但是却没有对点云格网化的选择方法和效果进行详细分析。相对于一般数据的格网化,点云数据存在数据量大、密度高等特点,如何根据点云特点选择合适的格网化方法是十分重要的。本文据此进行探讨,以获得有价值的结果和结论。
1 点云特点
三维激光扫描仪扫描目标物表面点的空间坐标后,得到点的集合,称为点云。点云具有如下特征:①立体化,点云数据能采集到物体表面所有采样点的三维空间坐标(X,Y,Z),仅展示点云信息就可以表达出被扫描物体的大致形态,因此其获得的目标物具有立体的表面信息。②数据量大,三维激光扫描仪由于其强大的激光特性,每min可以获得上万个点云,一站扫描所得点云可包含几万到几百万个。③密度高,现有扫描仪性能优良,有些仪器可以设置采样间隔最小达1 mm,使得扫描得到的点集密度非常高。④具有光学特性信息,扫描仪能够接收目标物的反射强度信息,使得不同点具有不同的颜色信息,即反射率。
2 格网化方法
按照内插点的分布范围,可以将内插分为整体内插、分块内插和逐点内插[11],整体插值是利用所有采样点进行整体的特征拟合,而分块插值是将研究区域进行分块,对各分块后的区域分别进行插值,逐点插值是分块插值的一种。点云由于其自身特点,一般使用分块插值,分块插值中常用的插值方法有加权反距离插值法、克里格插值法、最小曲率插值法、最邻近点插值法、三角形剖分插值法、多项式回归插值法等。其中,多项式回归法由于消除了原始点云的局部细节,不能对点云数据进行详细分析;最邻近点法适用于数据点位于网格节点上、分布较规则的数据类型,特别适合数据间隔均匀的插值,对散乱点云格网化效果较差。以上插值方法都不适用于海量点云的格网化处理。下面仅对其他4种适合点云特征的格网化方法作介绍。
2.1 4种格网化方法
1)克里格插值法。基本原理是利用变差函数根据点云中相邻变量的值所揭示的区域化变量的内在联系求取空间变量。优点是能表达出原始数据的趋势特征,因为其要求原始数据的估计值满足无偏性条件和最小方差条件,并且避免了孤立插值的情况。克里格法是一种应用十分广泛的插值方法,其有不同的变化形式,可以适于各种离散型的数据,获得的网格化精度较高。
2)加权反距离插值法。设平面内的一系列离散点已知位置信息和属性信息,其中任意一点P(X,Y,Z)的属性值可由其周围离散点的属性值通过距离加权插值求得。权值大小与待插值点和周围离散点间的距离有关,一般是两点间距离n次方的倒数。加权反距离插值法的主要思想是每一个观测值都受到邻近区域观测值的影响,且影响的大小与距离成反比。该方法可以通过改变权重来调整空间插值的结构,得到的插值结果整体性较好,缺点是其计算值受数据点集群影响严重,插值结果中存在孤立点数据插值面高于周围数据点的情况。
3)最小曲率插值法。通过多次迭代的方法求取格网节点数值,获得的插值面具有最小曲率,每个数据点也有最小曲率。
4)三角剖分插值法。将原始数据中各数据点用直线连接形成一系列三角形,并且保证所有的三角形不重叠、不相交,每个三角形面确定了网格节点的值。将所有的数据点都参与构造三角形,能够表达原数据的整体特性。该方法速度快,适合中等数量、均匀分布的数据的网格化,但研究区中较为稀疏的区域可能会形成截断的插值面。但当数据量足够时,对断线的保留具有其他方法不可比拟的优势。
不同的插值方法数学模型不同,遍历点云的方式也不同。克里格法极为灵活,网格化精度高;加权反距离插值法获得的结果具有较好的整体性,但容易受点集中孤立点的影响;最小曲率插值法能够遍历所有的数据点使曲率最小,图形光滑性好,容易使插值精确性存在偏差;三角剖分插值法速度快,能够有效保留断线,但是会形成插值断面。
2.2 插值步骤
分块插值法的主要步骤是:
1)定义一个邻域或搜索范围。由于点云数据为三维,首先需要在二维XY面内进行网格的划分。首先确定研究区的大小,即(Xmin,Xmax)、(Ymin,Ymax),则研究区二维边界4个方向的坐标分别为( Xmin,Ymax)、(Xmin,Ymax)、( Xmax,Ymin)、( Xmax,Ymax)。然后根据需要将研究区XY平面按X方向间隔m、Y方向间隔n,依次分割为m × n 个单元格,单元格的大小根据扫描区域及点云间隔来确定。设单元格边长为gx、gy,则网格的大小可以表示为:

这样就确定了网格的大小。
2)搜索落在此邻域内的数据点。在每一个网格内,搜索所有能垂直投影到该网格内的点云数据。
3)选择表达这有限个点云的空间变化的数学函数,即选择合适的内插方法进行插值。
4)为落在规则格网单元上的数据赋值。
分块内插方法中一个主要的问题就是如何确定分块大小。就目前技术而言,还没有一种合适的方法能够自动确定分块的大小。各种内插方法在不同的扫描对象和不同的点云类型下有不同的误差,应用时要根据各种方法的特点,结合应用的不同侧重,从内插精度、速度等方面选取合理的最优方法。
3 实验分析
不同格网化方法由于数学模型的差异使得格网化结果存在很大差别。本文以隧道点云监测数据为例,采用Scanner地面三维激光扫描仪对某运营地铁的隧道进行扫描,其扫描范围是水平方向360°、竖直方向305°,采用基于大地控制点的配准方法获得配准后原始点云如图1,点云数据量为118 285。为了便于分析,截取其中的部分数据进行分析,截取后数据如图2a所示,其数据量为21 094。将截取点云经滤波后封装,作对比分析,如图2b。

图1 隧道原始点云

图2 截取点云数据
首先要确定网格大小。研究区X的取值范围为(-4.324 0,1.422 9),Y 的取值为(10.539 3,17.083 1)。为更形象地表达格网化后隧道的整体趋势和局部细节,选取格网的大小为88×100。为了对比实验效果,本文控制其他变量不变,仅改变格网化方法。基于OpenGL软件平台编写了以上6种格网化方法的处理程序,格网化结果如图3~8所示。

图3 多项式回归插值结果
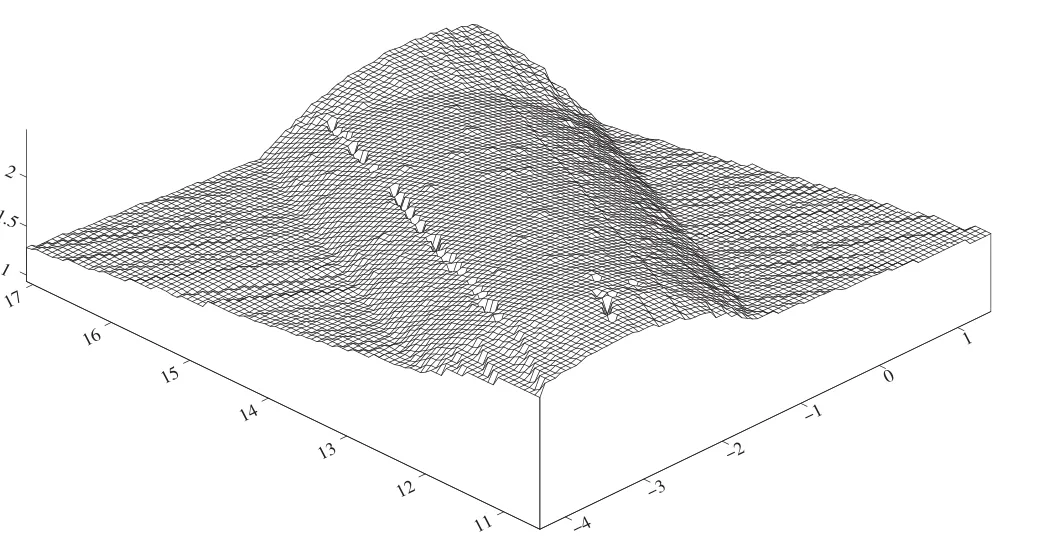
图4 最邻近点插值结果

图5 克里格插值结果

图6 加权反距离插值结果

图7 最小曲率插值结果

图8 三角剖分插值结果
从图中可以看出,不同点云格网化方法结果差异很大。多项式回归法将点云凸出的特征完全去除,失去了格网化的意义,可以认为不适用于点云数据处理。最邻近插值法针对散乱点云,格网整体平滑性差,细节表现不足。克里格法格网化表现出了细节信息,整体平滑性也很好,边缘处理效果不错,但是其存在的问题是当点云数量过大时,格网化精度会变差。加权反距离插值整体平滑性较好,细节表现不如克里格插值,其主要问题是点云边缘趋势明显高于内部,这是因为其孤立点对平滑的影响比较大。最小曲率插值法平滑性较好,保留了足够的细节信息,获得的结果较为美观,由于保证曲率最小,使得插值结果出现与实际情况不符的伪趋势现象。三角剖分法的插值在中间部分表达的隧道较为真实,受到原始点云存在缺失的影响出现了格网面断层的现象。
4 结 语
面对海量点云数据,格网化处理在提取点云信息、提高运算速度、改进滤波方法等方面发挥了很大作用。但格网化方法众多,如何根据点云特征选择合适的格网化方法十分重要。本文分析了一般格网化的方法,并基于点云特点进行总结,以地铁隧道点云数据为例进行实验对比,讨论了不同格网化方法对结果的影响,以及如何选择合适的格网化方法。
[1] 朱庆伟,马宇佼. 基于三维激光扫描仪的建筑物建模应用研究[J].地理与地理信息科学,2014(6):31-35
[2] 马俊伟,唐辉明,胡新丽,等. 三维激光扫描技术在滑坡物理模型试验中的应用[J].岩土力学,2014(5):1 495-1 505
[3] 李强,邓辉,周毅. 三维激光扫描在矿区地面沉陷变形监测中的应用[J].中国地质灾害与防治学报,2014(1):119-124
[4] 陈致富,陈德立,杨建学. 三维激光扫描技术在基坑变形监测中的应用[J].岩土工程学报,2012(增刊):557-559
[5] 周绍光,凡莉,向晶,等. 基于LiDAR点云海岛的DTM生成算法研究[J].山东科技大学学报:自然科学版,2015(3):53-61
[6] 靳生洪,杨鸿海,王莲玉. 基于格网化LiDAR点云数据坡度滤波方法的研究[J].测绘与空间地理信息,2013(6):154-156
[7] 卢秀山,黄磊.基于激光扫描数据的建筑物信息格网化提取方法[J].武汉大学学报:信息科学版,2007(10):852-855
[8] 黄承亮,向娟. 基于三维TIN的格网化点云数据特征提取[J].测绘科学,2010(增刊):127-128
[9] 常明,康志忠. 利用激光点云的规则面微小变形统计分析[J].测绘科学,2016(3):138-144
[10] 邬建伟,马洪超,李奇. 顾及语义的机载LiDAR点云格网化方法[J].测绘科学技术学报,2008 (2):87-89
[11] 李志林,朱庆. 数字高程模型[D]. 武汉:武汉大学出版社,2003

