基于MLR-WNN的大坝变形预测

杨 庆，任 超

(1.桂林理工大学测绘地理信息学院，广西桂林541004；2.广西空间信息与测绘重点实验室，广西桂林541004)

0 引 言

受温度、水压和时间效应等诸多因素共同影响，大坝在运营过程中往往会发生不同程度的形变，及时掌握大坝变形的演变规律并作出准确预报，对大坝安全具有重要意义[1]。早期传统的大坝变形预测方法有回归分析法、灰色理论和时间序列法等，如常见的多元线性回归模型(Multivariable Linear Regression，MLR)取得了较好的效果[2]。但在实际问题中，更常见的是非线性、非平稳时间序列。由于大坝变形受多种影响因素共同影响，呈现出高度的非线性和非平稳性，难以建立较为准确的变形量与影响因素之间复杂的关系模型，预测效果不佳[3]。目前，小波神经网络(Wavelet Neural Networks，WNN)模型被广泛用于非线性、非平稳性时间序列预测，其具有极强的自学习和非线性动态处理能力，在非线性系统建模和时间序列预测中表现出优越性，可以有效弥补多元线回归模型在处理非线性数据方面的不足，具有较高的精度[4]。任超等[5- 6]直接依据历史变形数据进行建模分析，来进行大坝变形预测，没有充分考虑影响因素与大坝变形量的关系，不能更符合实际地反映出大坝变形规律[7]。文献[8]指出，一个变化异常复杂的非线性、非平稳随机序列很难使用单一模型进行有效预报。单个预测方法往往都有各自的不足，难以获得完全的信息量，误差较大，而恰当的组合模型则可以实现优势互补，达到减少误差的目的[9]。因此，本文充分考虑了影响因素对大坝变形的影响，并采用组合模型的思想，将多元线性回归和小波神经网络相结合，充分发挥两者各自的优势，将有望对大坝变形中隐含的特征信息进行多层次、多角度挖掘和分析，从而提高预测精度。

1 基于MLR-WNN的大坝变形预测

1.1 多元线性回归原理

多元线性回归模型是反映多个影响因素与因变量之间的一种关系模型，其理论模型为

yi=β0+β1x1+β2x2+…βpxp+ε

(1)

式中，yi为实测变形量；β0为模型常数项；βp为模型系数；x为影响因子；ε是随机误差，E(ε)=0。

1.2 WNN原理

小波神经网络是一种把小波基函数作为隐含层激励函数的多层前馈神经网络，具有信号向前传播的同时误差向后传播的特点。在信号传递过程中，信号从输入层经隐含层神经元逐层处理，最后到达输出层。输出层“判断”输出结果是否是期望输出，若是则输出结果，否则进入反向传播过程。反向传播过程根据网络预测误差更新网络连接权值、尺度因子和位移因子，使预测输出无限接近期望输出，直至达到预测要求，具体可参照文献[4， 10-11]。

1.3 算法步骤

大坝变形的影响因素主要分为水位、温度、时效3部分。库水位决定大坝上游静水压力，而静水压力是坝体上最主要的荷载，是引起大坝变形的主要因素之一。温度分量描述的是气温荷载作用下效应量的弹性变化部分，其变化会引起坝体变形。时效分量是除了水位、温度荷载以外的诸因素所引起的因变量随时间变化的部分。

本文利用小波神经网络模型在非线性系统建模和时间序列预测中的优越性，将其引入到多元线性回归模型中，有利于从多角度、多层次地挖掘大坝变形信息，提高预测精度。设大坝在不同时间段的变形序列为{Y(x)=(tx，Hx，Tx)，x=1，2，…，n}，其中t为时效分量，H为上游水位影响因子，T为温度影响因子。预测流程见图1，即首先对其进行多元线性回归预测，得到预测值Li和残差G，再利用小波神经网络对G进行修正，得到残差预测值Hi，进而得到最终大坝变形预测值w为

w=Li+Hi(i=1，2，…n)+ε

(2)

式中，ε为随机误差。

图1 模型预测流程示意

1.4 模型精度评定

为综合评定模型的精度，采用均方根误差(Root Mean Square Error，RMSE)和平均绝对误差(Mean Absolute Error，MAE)作为模型评价指标。MAE和RMSE分别表示为

(3)

(4)

2 算例分析

2.1 试验数据及分析

本文以某抽水蓄能电站下库大坝变形的监测数据为例，42期观测结果见表1。由表1可知，该大坝变形最大值为2.52 mm，最小值为-1.86 mm，相差4.38 mm，该大坝变形幅度较大，随机性较强，呈现明显的非线性。如果只用在非线性数据处理上存在缺陷的多元线性回归模型对大坝变形进行分析和预测，很难得到令人满意和可靠的结果。因此，本文将具有非线性数据处理优势的小波神经网络引入到多元线性回归模型中进行分析和预测，有利于两者各自优势的充分发挥。为验证本文算法的有效性和可行性，建立3种方案进行对比分析，方案1为多元线性回归模型；方案2为WNN模型；方案3为基于MLR-WNN的大坝变形预测模型。

2.2 组合模型的验证结果及分析

本文将表1中1～30期数据作为试验数据，31～40期数据作为测试数据，对大坝变形和影响因子建立多元线性回归模型，并对其产生的误差进行小波神经网络修正，各模型的计算结果见表2和图2。由表2、图2可知，方案1、2的预测结果不稳定，部分预测与实测值相差比较大；方案1的残差最大值为1.04 mm，部分预测值与实测值偏差较大；方案2的残差最大值为1.28 mm；方案3的预测值和残差均优于其他模型，残差最小值为0.03 mm，最大值仅为0.45 mm。显然，本文模型的预测值与实测值吻合最好，优于其他模型，预测精度较高，可以显示出大坝变形的总体趋势。

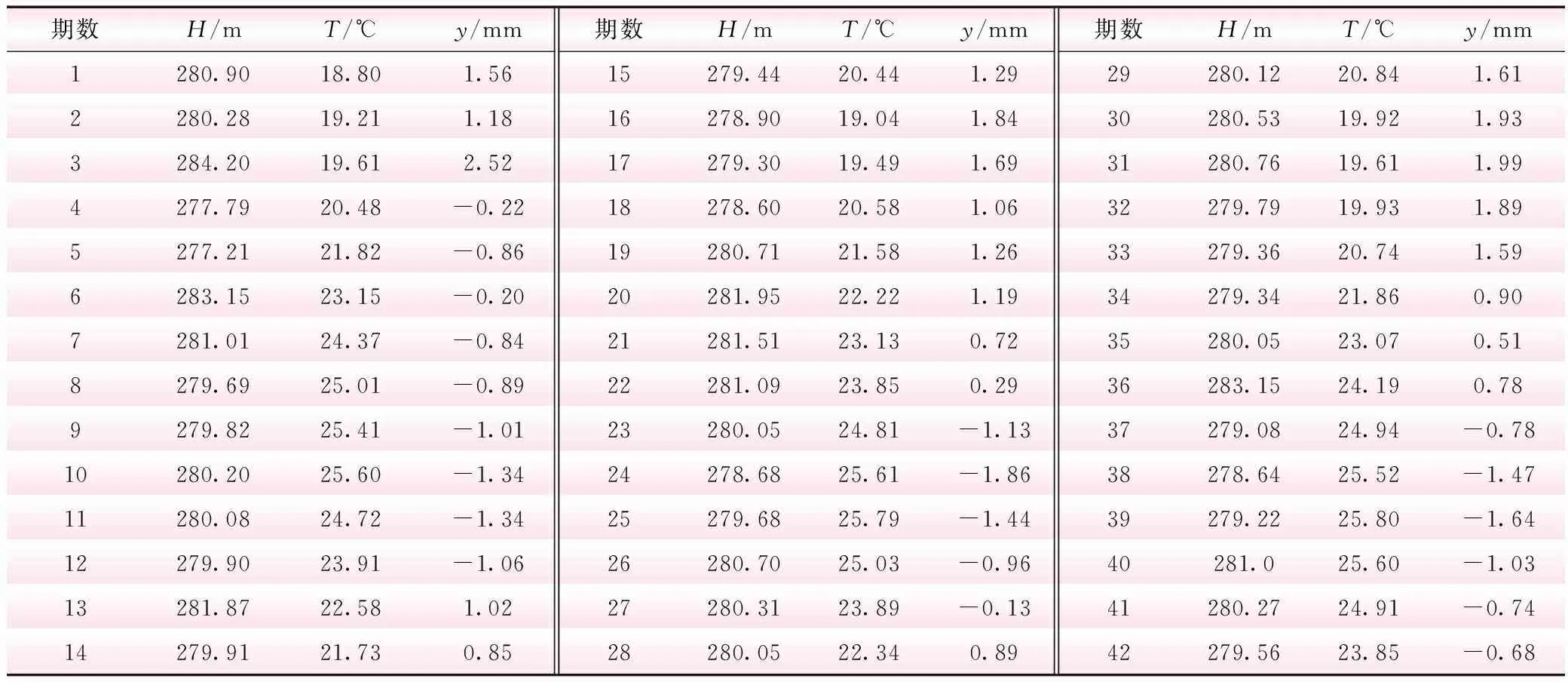
表1 某抽水蓄能电站下库大坝变形监测数据

表2 各模型变形计算结果对比 mm

图2 各模型预测结果与实际对比

为了进一步综合评定新算法的优劣，采用均方根误差和平均绝对误差2项指标进行评定。方案1的MAE和RMSE分别为0.483、0.603 0 mm；方案2的MAE和RMSE分别为0.36、0.504 1 mm；本文模型的MAE和RMSE分别为0.122、0.171 1 mm。显然，基于MLR-WNN模型的预测精度均优于多元线性回归和WNN模型，具有较高的预测精度，可信度较高。因此，本文算法具有一定的使用价值，可以用于大坝变形预测。

3 结 语

本文将在非线性系统建模和时间序列预测中有优势的小波神经网络引入到多元线性回归模型中，有效弥补了多元线性回归模型在处理非线性数据方面的不足。首先，对大坝变形和影响因子数据建立多元线性回归模型，并对其产生的误差进行小波神经网络修正。经理论和算例分析，并与多元线性回归和WNN模型对比分析表明，本文算法预测精度较高，可以用于大坝变形预测，为大坝变形预测研究提供了一种新思路。

参考文献：

[1] 蒋延臣, 张琴, 周立, 等. 基于小波方法的非线性回归模型研究[J]. 测绘学报, 2006, 35(4): 337- 341．

[2] 刘波, 张斌, 喻佳, 等. 基于多元线性回归模型的大坝变形预报研究[J]. 人民长江, 2010, 41(20): 53- 55．

[3] 王新洲, 范千, 许承权, 等. 基于小波变换和支持向量机的大坝变形预测[J]. 武汉大学学报： 信息科学版, 2008, 33(5): 469- 471．

[4] GUAN Che, LUH P B, MICHEL L D, et al. Very short-term load forecasting: wavelet neural networks with data pre-filtering[J]. IEEE Transactions on Power Systems, 2013, 28(1): 30- 41．

[5] 任超, 梁月吉, 庞光峰, 等. 基于经验模态分解和支持向量机的大坝变形预测[J]. 水电能源科学, 2014, 32(12): 67- 70．

[6] 任超, 梁月吉, 庞光峰, 等. 基于EEMD的大坝变形多步预测方法研究[J]. 大地测量与地球动力学, 2015, 35(5)： 816- 820．

[7] 万程辉, 何习平. 基于小波分析回归模型的大坝监测数据处理[J]. 测绘科学, 2009, 34(5)： 113- 115．

[8] HUANG N E, WU M L, QU W D, et al. Applications of Hibert-Huang transform to non-stationary financial time series analysis[J]. Applied Stochastic Models in Business and Industry, 2003, 19(3): 245- 268．

[9] 吴斌平, 岳攀, 鄢玉玲, 等. 考虑时间影响的神经网络组合模型对心墙堆石坝变形的预测研究[J]. 水力发电学报, 2016, 35(9)： 78- 86．

[10] 刘萍萍. 小波神经网络在大坝变形预测中的应用研究[D]. 西安： 长安大学, 2012．

[11] 邓勇, 张冠宇. 遗传小波神经网络在变形预报中的应用[J]. 测绘科学, 2012, 37(5)： 183- 186．