海上风机基础结构全寿命期静动力特性有限元分析

李 颖，喻旭明，王 滨，朱彬彬，张 杰

(1.浙江科技学院中德工程师学院，浙江杭州310023；2.中国广核新能源控股有限公司东南分公司，浙江杭州310015；3.中国电建集团华东勘测设计研究院有限公司，浙江杭州311122；4.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024)

0 引 言

我国海洋能资源十分丰富，具备开发建设海上风电的良好条件[1]，开发利用海上风能资源可以提高能源自给能力、促进经济社会可持续发展。根据“十二五”可再生能源规划，风电将继续获得大力发展，规划到2020年我国海上风电装机3 000万kW[2]。

海上风机多桩基础所处的地质结构复杂，承受风、风机、浪、流和地震等诸多随机荷载作用，且受到环境腐蚀、海床冲刷、基础动力软化、材料老化、构件缺陷和疲劳裂纹扩展的威胁。以往的研究主要集中在基于一种或两种控制标准开展的极端工况下单一荷载方向的结构静动力响应分析，且未考虑风机全寿命期内力变化。另外，要保证海上风电机组的安全运行也需要基础结构满足一定的控制指标，如基础转角、基频等。因此，非常有必要开展基于多重控制标准的海上风机多桩基础结构在各种复杂海洋环境荷载联合作用下的全寿命期静动力分析研究。

本文以江苏某海上风电项目为依托，基于静力分析、模态分析、地震分析等方法，研究了海上风机基础结构全寿命期内各特定阶段的静动力性能，并分析了风机结构在全寿命期内复杂荷载作用下的结构安全性与可靠性。

1 灌浆连接段建模理论

海上风机基础的灌浆连接部分一直是当前研究的难点。当进行结构整体静动力响应分析时，灌浆连接段部分的建模可以根据国内外普遍采用的简化方法，即将这一部分的灌浆材料、套管与桩按刚度等效处理：

(EI)等效=(E1I1)套管+(E2I2)灌浆材料+(E3I3)桩

(1)

式中，(EI)等效为结构桩基灌浆连接段经等效处理后的刚度；(E1I1)套管、(E2I2)灌浆材料、(E3I3)桩分别为套管、灌浆材料和桩的刚度。

表1 风机荷载

2 海上风机基础结构有限元模型

本文所选江苏某海上风机结构采用三桩导管架基础结构形式。三桩沿直径24 m的圆周均匀分布，桩径2.35 m，桩长61.0 m，壁厚26 mm，入土深度55 m。钢管桩与钢套管的环形空间内通过高强灌浆材料连接。主筒体直径为变直径4.7～3.0 m，主筒体与桩顶套管之间通过上部斜撑钢管与下部水平横撑连接。

本文采用有限元软件ANSYS进行计算，薄壁钢结构采用管单元Pipe59及二阶壳单元Shell63分别进行模拟，混凝土、灌浆材料采用Solid65单元进行模拟，下部桩土相互作用采用P-y法模拟。采用P-y曲线计算时，钢管桩与土体相互作用采用非线性弹簧单元模拟，根据地质资料提供的土的摩擦角、不排水剪强度等参数，结合《海上固定平台规划、设计和建造的推荐作法—荷载抗力系数设计法》[3]中土的P-y、t-z、Q-z曲线计算方法，将其转化为土的非线性约束弹簧。图1为该风机结构三桩导管架基础有限元模型。

图1 三桩导管架基础有限元模型示意

2.1 静力分析

风机的设计寿命一般为25年，综合考虑基础冲刷淘蚀、海洋生物生长、腐蚀与疲劳裂纹扩展等主要因素，将整个结构寿命期划分为特定的4个阶段进行分析，即服役起始、服役10年、服役20年、服役期止，其结构特点分别是①服役起始阶段是海床面未发生冲刷、海洋生物未生长、钢材未发生腐蚀及疲劳裂纹；②服役10年阶段是钢材的腐蚀及疲劳损伤相对较小，但基础冲刷淘蚀及海洋生物生长均已稳定；③服役20年阶段是钢材的腐蚀及疲劳损伤均有一定程度的累积；④服役期止阶段是规范要求支撑结构的强度、刚度、稳定性等多种指标仍需满足一定的控制标准。

海上风机基础常年受到风、波浪、海流和冰的共同作用，所受荷载条件比陆上风机更为复杂，在进行海上风机基础设计时如何合理组合结构所受载荷是关键。可将组合工况分为极限工况和正常运行工况。当风机轮毂中心距离塔筒底部80 m时，作用于塔架底端的海上风机荷载值见表1，风机荷载坐标轴见图2。

图2 风机荷载坐标示意

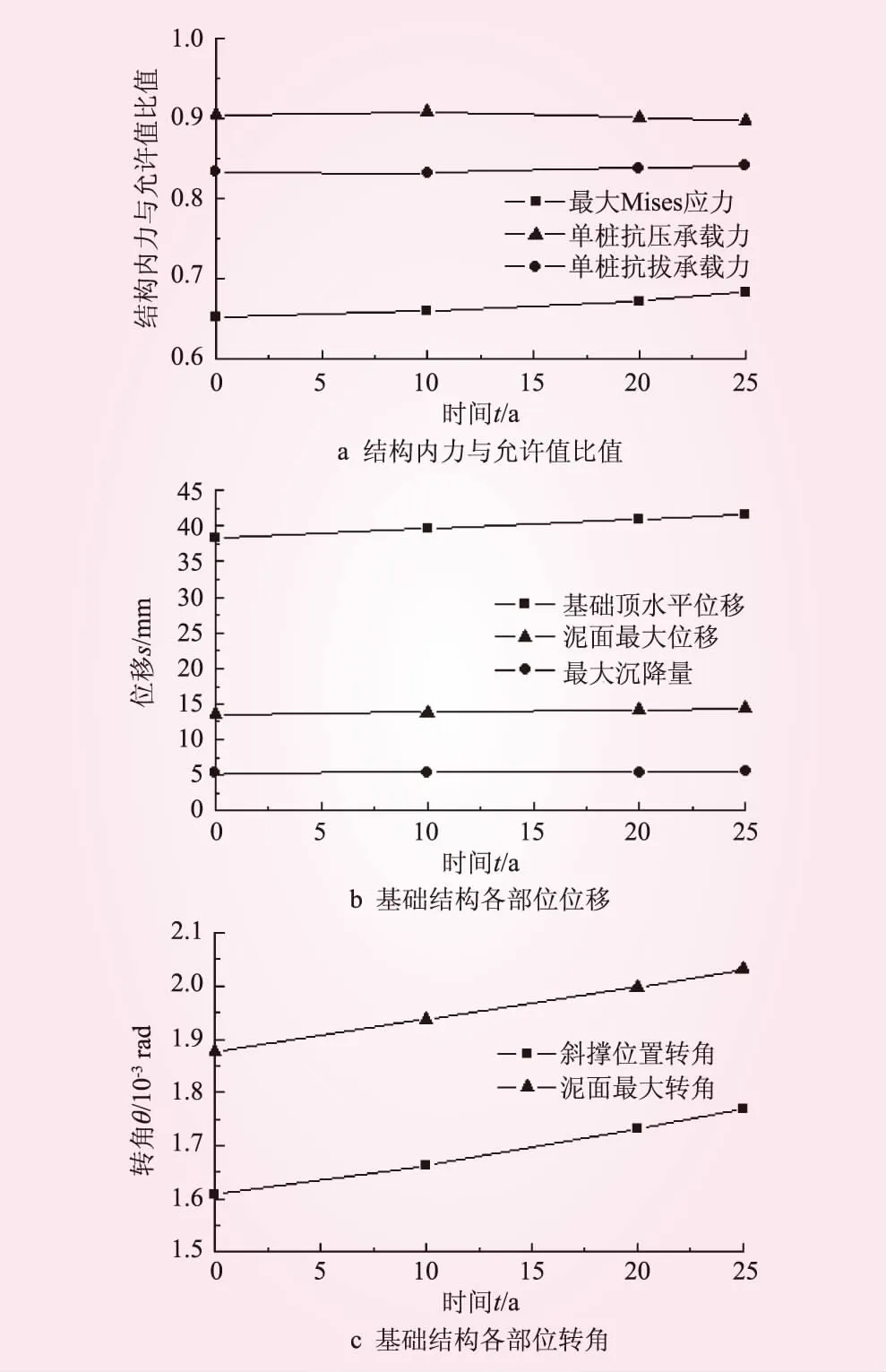
图3 海上风机结构全寿命期内力和位移变化

结构所承受的最大作用力与规范限值的比值均应小于1，因此本文中风机结构内力均为最大作用力与规范允许值的比值。图3为运行工况荷载条件下海上风机基础结构全寿命期内力和位移变化，其中结构内力和位移控制标准参考规范[4-7]。经过查表整理，静力工况下此风机基础结构应力允许值、单桩抗压承载力允许值、单桩抗拔承载力允许值、斜撑转角允许值分别为250 MPa、14 723.3 kN、7 868.3 kN、0.004 rad。随着风机服役年限增长，结构应力、基础位移与转角、单桩受拔最大作用力逐渐变大，单桩受压最大作用力逐渐减小。在风机全寿命期内，各项指标变化不大，并且满足规范允许值要求。

2.2 模态分析

海上风机结构承受的主要荷载是风和波浪，其具有明显的动力特性，海上高耸的风机结构体系在这些动力荷载作用下将产生显著的动力特性，而这些动力效应总是趋向于增加应力数值并损害结构的长期承载能力。因此，“风机-塔架-基础-地基”系统是一个相互作用高度耦合的动力系统，需对结构模型进行动力分析，以掌握结构的动力特性和响应。

本文采用有限元法对风电机组基础进行模态分析，对照叶片转动、塔筒自振频率以及波浪频率，以避免系统发生共振的可能性。通过模态分析，评价基础结构设计是否满足海上风电机组动力特性的设计要求。频率校核时，上部塔架采用梁单元Beam189建立，机舱、叶轮等采用质量单元mass21模拟，以质量块的形式施加。

图4为海上风机整体结构在全寿命期内的一阶固有频率变化，可以看出，结构一阶频率从服役起始的0.353 33 Hz降低至服役期止的0.349 77 Hz，变化幅度不大，仍然在整机频率允许范围0.268～0.394 Hz内，没有产生共振的危险。随着时间的增加，结构刚度在持续下降，会导致海上风机在全寿命期内具有产生较大塑性变形的风险，从而出现裂缝甚至破坏。

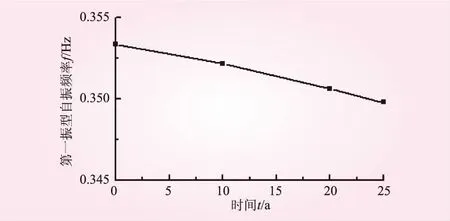
图4 海上风机整体结构在全寿命期内的一阶固有频率变化

2.3 地震工况下内力分析

本文根据地震相关资料，参考GB50011—2010《建筑抗震设计规范》[8]，采用相关地震反应谱模拟计算地震作用。地震影响系数曲线的阻尼调整系数按1.0采用，特征周期取0.9 s，结构阻尼比取0.05，水平地震影响系数按规范要求取0.20。在计算地震工况下各振型内力后，采用CQC方法进行振型组合，由于地震的随机性和地震方向的不确定性，地震输入考虑了X、Y、Z3个方向，方向组合系数取值分别为1.0、1.0、0.5。

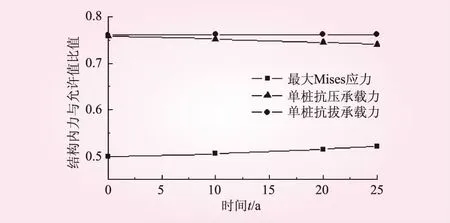
图5 地震工况下海上风机基础结构内力变化

地震工况下，此风机基础结构应力允许值、单桩抗压承载力允许值、单桩抗拔承载力允许值分别为312.5 MPa、18 404.2 kN和9 720.4 kN。图5为地震工况下基础结构在不同时期时的内力。结果表明，地震作用下全寿命期内结构单桩承载能力有所降低，但仍然不超过允许范围内。

2.4 海生物附着厚度敏感性分析

海生物生长是影响海上风机基础结构安全性能的一项重要因素，海生物的生长将改变海上风机基础结构的几何形状和表面状态，导致水动力荷载的增加，并改变支撑结构的动力特性，从而影响结构的动力响应和疲劳损伤。海生物生长附着范围为海平面附近至泥面附近，生长较为迅速，生长厚度在风机基础结构建成后一年即相对稳定。江苏海域已建工程的海生物附着厚度一般为50 mm，此时海生物的生长保持一种动态平衡的状态。

为保证海上风机基础结构在服役期内的安全，本文对服役期止的风机基础结构海生物附着厚度的敏感性进行研究，厚度分别取50、100 mm。计算时导管架结构海平面以下的结构外径分别增加50、100 mm，进行静力分析和模态分析。图6分别为不同海生物厚度时风机基础结构内力和固有频率变化，可以看出，海生物生长对风机基础影响较小，由于海生物附着，导致风机基础自重增大和水动力荷载增加，使得静力分析各项指标均有所增加。模态分析结果表明海生物生长对基础结构自振特性敏感性较低，基本不构成影响。

图6 不同海生物厚度时风机基础结构内力和固有频率变化

3 结 论

本文对江苏某海上风机三桩导管架基础结构分别进行了静力分析、模态分析与地震分析，得出以下结论：①静力工况下，随着海上风机服役年限的增长，结构应力、基础变形、单桩受拔最大作用力逐渐变大，单桩受压最大作用力、基础整机频率逐渐减小；②全寿命期内结构应力增大，承载能力有所降低，但仍然可以在场区发生地震的情况下安全工作；③海生物附着导致风机基础自重增大和水动力荷载增加，使得静力分析各项指标均有所增加，但海生物生长对基础结构自振特性基本不构成影响。

参考文献：

[1] 阳云, 桂武鸣. 中国风力发电的未来趋势[J]. 国内外机电一体化技术, 2010(5)： 41- 43．

[2] 刘林, 葛旭波, 张义斌, 等. 我国海上风电发展现状及分析[J]. 能源技术经济, 2012(3): 66- 72．

[3] SY/T 10009—2002 海上固定平台规划、 设计和建造的推荐做法—荷载抗力系数设计法[S]．

[4] GB/T 1591—2008 低合金高强度结构钢[S]．

[5] JGJ 94—2008 建筑桩基技术规范[S]．

[6] FD 003—2007 风电机组地基基础设计规定(试行)[S]．

[7] GB 50017—2003 钢结构设计规范[S]．

[8] GB 50011—2010 建筑抗震设计规范[S]．