基于2DPCA与稀疏表示的目标跟踪*

茅正冲， 黄舒伟

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

0 引 言

目标跟踪作为计算机视觉领域一项重要的核心技术，广泛应用于智能视频监控、目标行为分析、目标识别以及人机交互等领域[1～4]。

近几年，稀疏表示逐渐应用于目标跟踪[5，6]，并取得了很好的跟踪效果。2009年，Mei X等人[7]首次将稀疏表示的理论引入到目标跟踪领域，即L1跟踪系统。其核心思想是在粒子滤波的框架下，使用一组目标模板与平凡模板将每个候选目标线性表示。当目标候选所拥有的重构误差最小时，该候选目标被选定为跟踪的对象。随后，一些学者针对L1跟踪器不足提出了许多改进方法，Bao C L等人[8]对平凡模板系数附加上L1范数，使用加速最近梯度(APG)法,加快稀疏解的收敛速度，提高了跟踪效率。文献[9]提出了一种基于稀疏性的协同模型算法，同时使用了全局模板与局部模板对目标进行描述，融合了稀疏判别的分类器与稀疏性的生成式模型，还引入了有效方法计算置信度，有效地处理目标变化和减轻跟踪过程中的漂移问题。

本文简要概述了稀疏表示的原理，详细介绍了改进的算法，并通过实验得到跟踪结果与数据证明改进的算法与一些主流算法相比的优势所在。

1 基于稀疏表示的目标跟踪算法

稀疏表示的本质是一个线性近似的问题，候选目标y都可以表示为字典C=[c1,c2，…，cn]下的线性组合，即

y=Ca=c1a1+c2a2+…+cnan

(1)

式中a=[a1,a2,…,an]T∈Rn为在该冗余字典下候选目标的稀疏系数;n为目标模板的个数。通常在跟踪过程中会出现噪声、遮挡等情况，引入平凡模板I=[i1,i2,…,in]∈Rd×d对稀疏表达式进行描述

(2)

式中e=[e1,e2,…,en]T为平凡模板的系数向量。为了求得合适的解，需要对稀疏系数a约束，使用L0范数求解

(3)

求解式(3)方程在数学上是一个NP-hard问题，L0范数非凸且高度不可微，到目前为止没有有效算法来解决，使用L1范数来代替L0范数，即

(4)

通过拉格朗日乘数法可以将上述约束问题转换为无约束问题，即

a*=argmin 0.5‖xi-Cai‖2+λ‖ai‖1

(5)

式中λ为一个常数，用来平衡重构误差与稀疏性，式(5)可以通过最小角回归(LARS)算法求解。

2 改进目标跟踪算法

对于L1跟踪算法存在许多不足之处，当候选区域选择了背景区域或者在被遮挡的情况下，使用目标与平凡模板表示候选样本时，平凡模板的系数不再为零，从而整个系数均不再稀疏。L1模板的计算十分复杂，不适用于目标跟踪。

2.1 二维主成分分析

与传统的主成分分析(principal component analysis,PCA)算法相比，二维主成分分析(two-dimensional PCA,2DPCA)是基于二维矩阵而不是一维的向量，图像矩阵不需要转化为向量，保留了原来数据的多维结构。因此，使用2DPCA较图像的特征提取在计算上更有效:

1)计算样本总体的散度矩阵

(6)

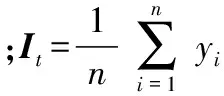
2)计算总体散度矩阵G的特征值

λ1≥λ2≥…≥λn

(7)

3)计算与特征值对应的单位正交特征向量u1,u2,…,un。

4)保留前t个最大特征值所对应的标准正交特征向量，构成特征子空间U

(8)

2.2 L2跟踪算法

使用2DPCA得到的子空间U构成稀疏表示的冗余字典，候选目标可以由U来进行稀疏表示，即

y=Ua+e=u1a1+u2a2+…+unan

(9)

式中a=[a1,a2,…,an]∈Rn为稀疏表示的稀疏系数，通过L2范数对其进行求解，即

(10)

式中λ为一个常数，用来平衡重构误差与稀疏性;L2范数约束项主要作用为：获得远低于L1范数的稀疏度的解a;使得最小化的解更加的稳定。令

(11)

可以得到

a=(UTU+λI)-1UTy

(12)

求得系数后，可以用U与a表示残差向量e，即

e=y-Ua

(13)

令P=(UTU+λI)-1UT为投影矩阵，可以看出，P是独立于y的，因此，只需处理每一帧图像，不管有多少候选目标，P只需计算一次。可以通过a*=Py将候选目标y投影到P上来。

2.3 动态模型

在粒子滤波中，使用p(xt|xt-1)表示2帧之间的动态模型，本文选取仿射变换的6个参数对目标的运动状态进行描述，目标状态变量xt为

xt={xt,yt,θt,st,at,φt}

(14)

式中 6个参数依次为水平方向平移、垂直方向平移、旋转角度、尺度变化量、纵横比以及斜切角。一般情况下，状态转换模型服从高斯分布，即

p(xt|xt-1)=N(xt;xt-1;ψ)

(15)

式中ψ为对角协方差矩阵，其元素为6个仿射变换参数的方差。

2.4 目标观测模型

通常观测似然度函数一般选择其重构误差，即

(16)

表示目标候选的似然概率，当候选目标稀疏表示的重构误差越小，其稀疏越可靠。但是面对有遮挡的目标，使用式(16)作为衡量标准不能够很好地对目标进行跟踪，在似然度函数中，引入重构误差e的L1范数，以提高目标跟踪的鲁棒性与跟踪的精度

(17)

式中δ为一个常数(本文设置为0.5)。

将N个候选目标人作为视觉皮层的神经元细胞，将目标模板作为外部的输入信号，当神经元接收外界的输入信号时，计算每个神经元得平均激活率ηi

(18)

即当响应外部信息的大脑皮层神经元平均激活率越高，该神经元与外部信息相符合程度越高。应用到目标跟踪中，即目标的候选与模板的相似度越高。在相似度函数计算公式中加入平均激活率，使得目标跟踪更具有准确性与鲁棒性

(19)

2.5 模板更新

在跟踪过程中未考虑到光照、遮挡以及姿势变化等因素的影响，使用固定的模板往往会导致跟踪失败。若是频繁的更新模板，跟踪器以错误的跟踪结构来更新模板，造成目标的丢失。本文采用增量子空间学习的方法对模板进行更新，以减轻遮挡对目标模板的影响。

3 实验结果与分析

3.1 仿真环境

实验硬件平台是Intel (R) Core i5 CPU M 480 @2.67 GHz的计算机，在MATLAB 2012环境下实现。在实验中λ=0.05，目标的第一帧由手动标定，在目标区域缩放至32×32，选取2组视频序列进行实验。取粒子数为600，通过与多示例学习(multiple instance learning,MIL)[13]与视觉增量学习(incremental visual learning,IVT)[14]2种算法对比，并用矩形框将跟踪的结果显示出来(1号方框为本文算法，2号方框为IVT算法，3号方框为MIL算法)，验证本文算法的有效性与合理性。从公平开的视频库中选取3个视频序列实验，在视频跟踪过程中经常会出现不同程度的光照变换、姿势变化、局部遮挡以及快速运动等。

3.2 定性分析

在Cavia 2视频序列中，目标经历了严重的遮挡与尺度的变化。图1给出了部分跟踪结果。第95帧和第103帧时，MIL算法丢失了目标，在随后几帧的更新中又重新找到了目标。195帧时目标被行人大面积遮挡时，MIL算法发生了漂移无法再恢复导致跟踪的失败，这是由于未考虑背景因素。对于IVT算法虽然未漂移，但是跟踪框变得很小，精度很差。通过图1的结果可以看出，本文的算法始终可有效地对目标进行跟踪，体现了其跟踪的鲁棒性与准确性。

图1 Cavia2视频序列部分帧的跟踪结果

Car11视频序列中存在明显的光照变化，车辆在夜间行驶，光线条件较差，跟踪的目标车辆在与来车会车时光照会发生明显的变化。这些变化可以在Car11的第200帧与260帧看出。部分帧的跟踪结果如图2所示。IVT模型可以很好地克服光照变换造成的影响。MIL模型在第32帧时目标开始逐渐的漂移，到210帧时目标已完全漂移并且再也无法捕获目标。本文算法存在有光线变化与相似目标干扰情况下依旧可以很好地对目标进行跟踪。

图2 Car11视频序列部分帧的跟踪结果

通常情况下假设跟踪的目标运动变化比较微弱，在实际中对于快速运动的目标一些算法无法对其进行跟踪。采用Deer视频序列，目标一直处于运动变化中，跟踪困难。部分帧的跟踪结果如图3所示。在第26帧时使用IVT模型的目标开始漂移且无法重新捕获目标，而MIL算法在第37帧也完全丢失了跟踪目标。本文算法成功稳定地跟踪快速运动的目标。

3.3 定量分析

为了更加准确地评价本文算法的优劣性，必须采用定量分析方法。本文衡量的准则是跟踪结果与真实值中心的位置误差与重叠率。中心点误差为

图3 Deer视频序列部分帧的跟踪结果

(20)

式中 (x0,y0)为真实目标中心的坐标；(xt,yt)为t时刻跟踪算法计算的目标中心的的坐标。误差值越小表示跟踪的目标更加准确。图4为不同算法间部分帧测试视频中的误差曲线。表1列出了不同算法的平均中心误差。本文提出的算法误差值较小，误差分布比较平稳。

图5 不同算法的重叠率曲线

重叠率为真实目标区域与预测目标区域间重叠面积的比率

许多文献的研究表明，一般情况下，系统的不变集包含了垂直顶部不稳定平衡点，但并不能保证系统运动至不稳点，系统将在不变集上做周期运动，这种情况下，须采取另一种控制律打破这种周期运动，这种切换控制的稳定性由开关定律得以保证。一种较为常见的处理方法是，在系统运动至不变集过程中，当系统的状态变量满足线性化条件时，将系统线性化，采用线性系统理论来设计控制器[3][5]。线性系统理论已经成熟，这里不做过多讨论，线性化带来的误差处理方法可参见文献[5]。

(21)

式中Rg为真实目标矩形框区域；Rt为不同跟踪算法预测目标矩形框区域。式(21)分子为两者的交集，即重叠部分，分母为两者的并集，即面积之和。重叠率越高，表示目标跟踪算法的效果越好，一般认为重叠率高于0.5，表示目标正确跟踪。不同算法的重叠率曲线如图5所示，平均重叠率如表2。

表2 不同算法的平均重叠率

4 结束语

本文使用2DPCA与稀疏表示方法进行目标跟踪，2DPCA提取的特征构成字典与L2范数最小化进行结合，大幅提高了跟踪的实时性与准确性。使用了几组受到光照变化、姿势变化、遮挡以及快速运动影响的测试视频与其他算法进行了比较，实验结果表明：能够很好地实现目标跟踪并且具有较强的鲁棒性，未来将针对算法精度与实时性进行完善。

参考文献:

[1] Shu C F,Hampapur A,Lu M,et a1.IBM smart surveillance system(S3):An open and extensible framework for event-based surveillance[C]∥Proceedings of the IEEE International Confe-rence on Advanced Video and Signal-Based Surveillance,Como,Italy,2005:318-323.

[2] Shah M,Javed O,Shafique K.Automated visual surveillance in realistic scenarios[J].IEEE Transactions on Multimedia,2007,14(1):30-39.

[3] 谷 静,史健芳.分布式粒子滤波算法在目标跟踪中的应用[J].传感器与微系统,2014,33(8):158-160.

[4] 施 滢，高建坡,崔 杰,等.分块多特征自适应融合的多目标视觉跟踪[J].传感器与微系统,2015,34(9):128-131.

[5] Gmbner H,Gmbner M,Bischof H.Real-time tracking via online boosting[C]∥Proceedings of the British Machine Vision Confe-rence,Edinburgh,UK:BMVA,2006:47-56.

[6] Gmbner H,Leistner C,Bischof H.Semi-supenrised online boosting for robust tracking[C]∥Proceeding of the 10th European Conference on Computer Vision,Marseille,FraJlce:Springer-VerLag,2006:47-56.

[7] Mei X,Ling H.Robust visual tracking using L1 minimization[C]∥Computer Vision,Anchorage,Alaska:IEEE,2009:1436-1443.

[8] Bao C L,Wu Y,Ling H B,et al.Realtime robust L1 tracker using accelerated proximal gradient approach[C]∥ 2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR),IEEE,2012:1830-1837.

[9] Zhong W,Lu H C,Yang M H.Robust object tracking via sparsity-based collaborative model[C]∥IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Rhode Island,2012.

[10] 杨大为,丛 杨,唐延东.基于粒子滤波与稀疏表达的目标跟踪方法[J].模式识别与人工智能,2013,26(7):680-687.

[11] Li J Y,Lu X F,Ding L Y,et al.Moving target tracking via particle filter based on color and contour features[C]∥Proceeding of the 2nd International Conference on Information Engineering and Computer Science,Wuhan,China,2010.

[12] Wang D,Lu H C,Yang M H.Online object tracking with sparse prototypes[J].IEEE Transactions on Image Processing,2013,22(1):314-325.

[13] Babenko B,Yang M H,Belongie S.Visual tracking with online multiple instance learning[C]∥Conference on Computer Vision and Pattern Recognition,Florida:IEEE,2009:983-990.

[14] Ross D,Lim J,Lin R S,et al.Incremental learning for robust visual tracking[J].International Journal of Computer Vision,2008,77(1):125-141.

[15] Kwon J,Lee K M.Visual tracking decomposition[C]∥Procee-dings of the International Conference on Computer Vision and Pattern Recognition,San Francisco,USA,2010:1269-1276.

[16] 袁广林,薛模根.基于稀疏稠密结构表示与在线鲁棒字典学习的视觉跟踪[J].电子与信息学报,2015,37(3):536-542.