一种优化WSNs节点部署的变步长虚拟力算法*

张俏薇， 陈俊杰

(东南大学 仪器科学与工程学院，江苏 南京 210096)

0 引 言

无线传感器网络[1](wireless sensor networks,WSNs)节点的初始部署通常为随机部署，导致覆盖率较低，产生监测空洞。为解决该问题，需调整节点的部署位置，以降低监测空洞和节点部署冗余。虚拟力[2]算法因其实现简单、应用灵活、优化效果明显等优点，成为目前移动传感器节点部署的主要优化方法之一。

国内外对基于虚拟力算法的覆盖策略进行了许多研究。刘军[3]针对现有虚拟力算法中存在覆盖效率和覆盖率不统一的问题，提出了利用传感器节点感知扇形区域质心点间的斥力调节感知方向，利用虚拟力和覆盖冗余度共同控制传感器的转动。Brust M R等人[4]考虑到保证无人机航拍的三维覆盖率时的定位困难，借鉴分子几何学中电子对围绕中心原子安排自身位置的思想，提出了一种基于虚拟力算法的自动定位3D簇算法。Khoufi I等人[5]针对复杂假设条件下的应用场景，设计了一种躲避障碍的虚拟力算法，可以避免节点震荡的问题，并可以在分配机制下检测到节点部署结果。Li Y等人[6]提出了一种均衡能量的虚拟力算法，引入了一种均匀度函数的评估函数评估WSNs节点部署分布的均匀性，实现了以较少的能耗达到节点部署的高覆盖率和高度均匀性。前述研究并未考虑到虚拟力算法后期稳定性差这一缺陷，而稳定性差会降低覆盖效率，影响实际应用效果，增加部署成本。

最小均方(least mean square,LMS)自适应滤波算法具有计算量小、易于实现且对信号的统计特性具有稳健性等优点而得到广泛应用[7]。本文借鉴LMS自适应滤波函数中基于sigmoid函数的变步长函数，对传统虚拟力算法的步长函数进行了改进。仿真实验表明：改进算法可以在维持传统虚拟力算法优越性的基础上，改善后期稳定性差、稳态误差大的缺点，保证了部署效果的有效性。

1 节点感知模型

本文采用0—1圆盘感知模型。假设WSNs监测区域S为二维平面的矩形，离散化为K个网格，每个网格采用网格点进行描述。每个网格的面积为1，单位化后，使得监测区域定义为一个由许多网格点组成的集合

C={a(x1,y1),a(x2,y2),…,a(xK,yK)}

(1)

式中K为网格点的数目，需要根据监测区域的目标和测量精度要求确定。

为了研究的针对性，本文设定感知半径为一合适常量r。假设每一传感器节点s放置于位置(xs,ys)，对于任一点d，位置为(xd,yd)，s～d的欧氏距离为l(s,d)，d点被s点监测到的概率与传感器节点感知半径r的关系为[8]

(2)

2 基于sigmoid函数的变步长虚拟力算法

在监测区域，将n个移动传感器节点随机分布在L×W的大面积目标区域，记为集合U

U=[u1,u2,…,un]

(3)

在该监测区域建立坐标系，使区域的4顶点坐标分别为(100,100)，(L+100,100)，(W+100,100)，(L+100,W+100)，节点ui坐标(xi,yi)，i=1,2,3,…，感知半径为rp。在此坐标系下构成的WSNs中，初始节点分布不均匀，覆盖率低。

传统虚拟力算法[9]中，假设传感器节点之间，节点与网络格点之间存在着力的作用，使节点运动。该模型假定[9]：1) 所有节点都是可移动的；2) 所有节点具有全向传感器，且其感知区域是一个以节点为圆心的圆形；3) 所有节点的位置信息是可知的；4) 所计算出的移动方案可以有效执行；5) 所有节点的质量相同。

每个节点ui可能受到3种力的作用：来自边界的斥力FiB；来自网格节点的引力FiD；来自其他节点uj的引力或斥力Fij。Fij大小由两个节点ui与uj之间的距离决定。设置距离阈值为dmax，节点ui所受到的合力Fi为

(4)

(5)

式中dij为节点ui与节点uj之间的欧氏距离；αij为从节点ui到节点uj的方向角；ta和tr分别为引力和斥力的系数，当两个节点之间的距离小于阈值dmax时，受到斥力；大于阈值时，受到引力；等于阈值时，受到的力为0。

根据牛顿力学定律，节点受力后，会产生加速度

(6)

式中ai为传感器节点ui的加速度;mi为传感器节点ui的质量。

传感器节点ui的运动速度为

vi=aiti

(7)

在相同的时间间隔中，节点的运动距离di正比于加速度ai的值

(8)

根据传统虚拟力算法的实现过程可知，理想情况下，如果2个节点之间的距离十分近，会产生非常大的斥力，导致节点移动速度较快。但在实际应用中，每个节点的移动速度有最高速度限制，且速度值vi通常为常数，即

vi=max_step

(9)

传感器节点ui的速度值，即为每次迭代节点的移动步长μi

μi=vi

(10)

可知传统方法易导致迭代效果达到了最佳后，继续迭代，后期稳定性下降。因此，需要对步长选取进行调整。

根据文献[10]的分析，改进的LMS算法的步长函数调整方式如下：在初始收敛阶段，步长应较大，以便有较快的收敛速度和对时变系统的跟踪速度，在算法收敛后，应保持很小的调整步长以达到很小的稳态误差，获得较好的稳定性。步长的变化趋势应随时间或者迭代次数的增加而减少，减小的幅度应越来越大，直至最后趋近于0。

文献[5]根据sigmoid函数提出了改变步长因子μi的设想：μi为e(t)的sigmoid函数

(11)

式中α为控制sigmoid函数的常数，决定曲线上升的速度；β为控制sigmoid函数取值范围的常数；t为迭代次数；e(t)为每次迭代的误差，即每次迭代的覆盖空洞率。μ(t)与e(t)的函数曲线如图1所示。

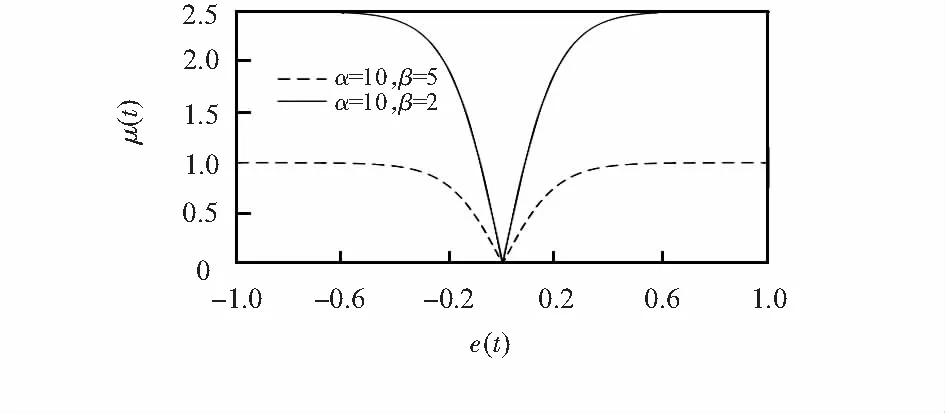
图1 e(t)与μ(t)的关系曲线

可知，随着e(t)减小，μ(t)随之减小，且减小的幅度由小变大。可实现对传统虚拟力算法缺陷的弥补，在收敛达到一定程度后，使最终结果趋于稳定。

3 仿真实验与结果分析

通过仿真实验验证算法对提高传统虚拟力算法后期稳定性的有效性，并对算法性能进行对比分析，包括收敛性能、覆盖率。通过引入基于sigmoid变步长函数对节点的移动速度进行干预，提高了节点后期的覆盖效果的稳定性，同时提高了迭代前期的收敛速度。并与线性函数变步长和二次函数变步长算法进行了对比分析。仿真实验参数设置如表1所示。

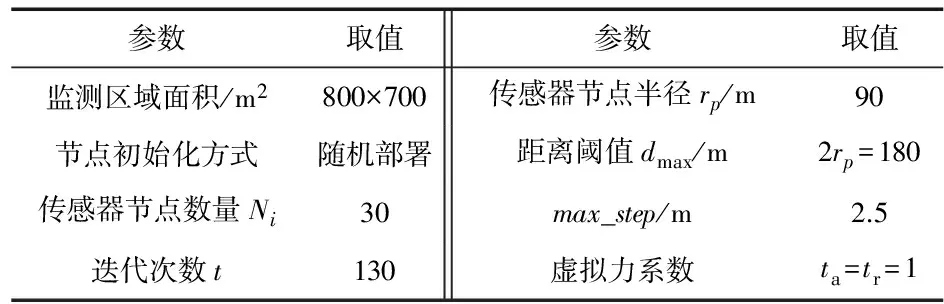
表1 仿真实验参数

根据传感节点感知模型和监测区域的建立，任意一个无线传感器节点均可以部署到任何一个被划分的网格点上，实现监测区域覆盖率量化，用比值q表示评价WSNs节点部署性能优劣的目标函数，即

q=sum/K

(12)

式中sum为被覆盖的网络点数；K为总网络点数。

本文设计了3种变步长的函数进行对比分析，分别为线性函数、二次函数和基于sigmoid函数的变步长函数。

仿真初始阶段，传感器节点随机分布于监测区域。分别在传统的虚拟力算法、线性函数变步长的虚拟力算法、二次函数变步长的虚拟力算法和基于sigmoid函数变步长的虚拟力算法的作用下，分别进行位置更新。

定义线性变步长的虚拟力算法的步长函数为

μL(t)=aLt+bL

(13)

式中aL，bL分别为线性函数的参数。

定义二次函数变步长的虚拟力算法的步长函数为

μQ(t)=aQt2+bQ

(14)

式中aQ，bQ分别为二次函数的参数。

定义sigmoid函数变步长的虚拟力算法的步长函数为

(15)

式中aS，bS分别为基于sigmoid函数变步长函数的参数。

各自选取最优参数，进行仿真实验。

传统虚拟力算法仿真结果如图2所示。线性函数变步长、二次函数变步长和基于sigmoid函数变步长的虚拟力算法仿真结果如图3所示。

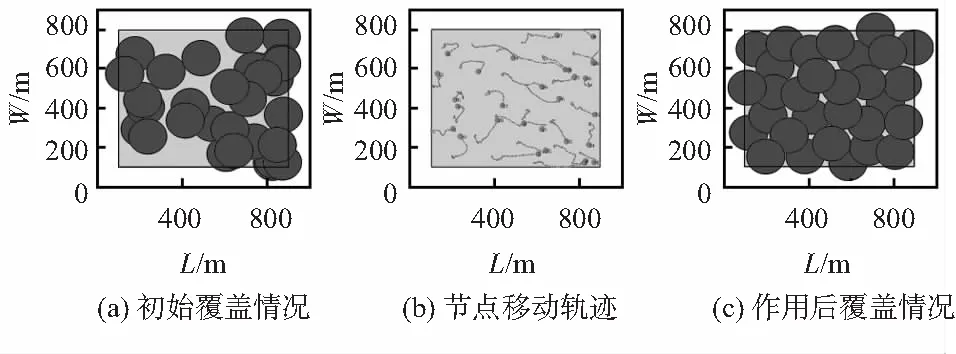
图2 传统虚拟力作用情况

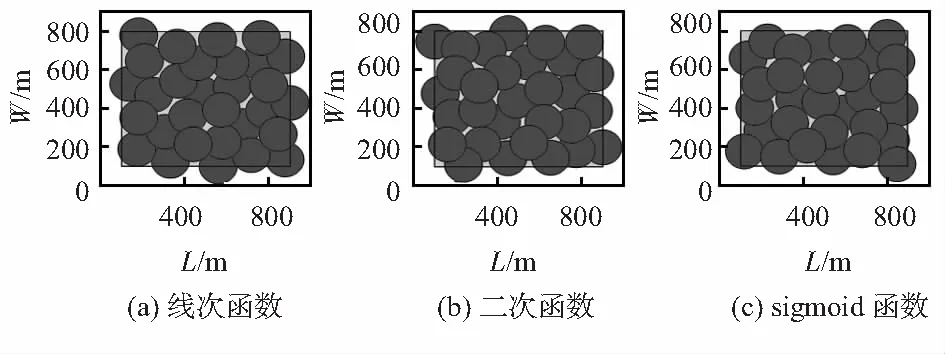
图3 变步长函数覆盖情况

如图4所示，传统虚拟力算法后期的覆盖率数据不稳定。线性变步长的虚拟力算法可以加快收敛速度，用了比较少的迭代次数即达到了最佳覆盖率，效果比传统虚拟力算法好很多。二次函数变步长的虚拟力算法，收敛速度较传统虚拟力算法快，但其不稳定性较传统虚拟力算法更大；可以明显看出：基于sigmoid函数的变步长虚拟力算法的收敛速度最快，迭代效果最佳，后期结果的稳定性提高。4种函数性能指标如表2所示。

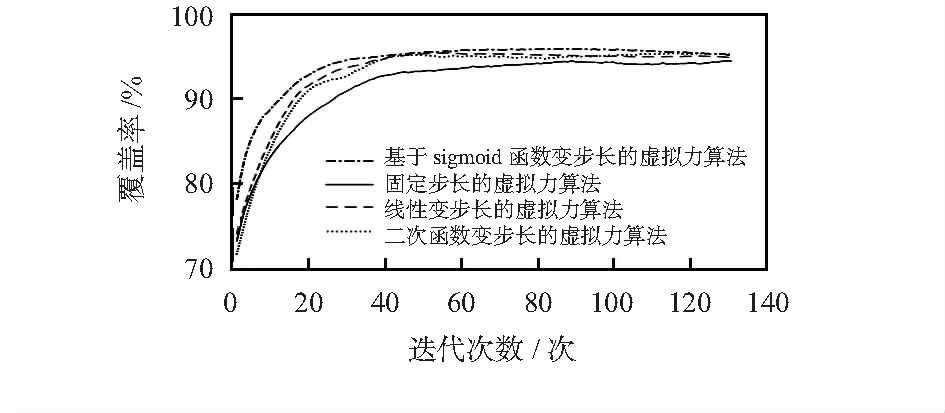
图4 覆盖率变化过程对比

性能指标传统函数线性函数二次函数基于sigmoid函数覆盖率最优值/%94．4595．3695．3595．89迭代次数89．0054．00115．0087．00覆盖率最差值/%92．7994．8394．6995．09均值91．7295．1095．0595．60方差值0．04440．00150．00160．0022

可知：虽然基于sigmoid函数的变步长虚拟力算法达到覆盖率最优时迭代次数不是最少，稳定性与线性函数和二次函数变步长相比略差一点，但其覆盖效果最好。与传统虚拟力算法相比，覆盖率均值提高了4.23 %，覆盖率最优值提高了1.52 %，稳定性提高了95.05 %。基于sigmoid函数的变步长虚拟力算法在保证收敛速度的同时，有效提高了覆盖率，并且极大地提高了后期稳定性。

4 结 论

提出了变步长改进的虚拟力算法。在建立的监测模型基础上，通过借鉴LMS自适应滤波算法中变步长函数，研究了线性函数、二次函数和基于sigmoid函数的变步长虚拟力算法对覆盖效果的改进情况。通过仿真结果比较发现，基于sigmoid函数变步长的改进算法效果最好，与传统虚拟力算法相比，在保证收敛速度的同时，极大地提高了后期阶段的数据稳定性。

参考文献:

[1] 李双明，武庆威.采用RSSI提高无线传感器网络定位精度的算法[J].无线电工程，2015,45(2)：8-10.

[2] 毛科技，徐 慧，方 凯，等.基于虚拟力的WSNs路由协议设计与实现[J].传感器与微系统，2017,47(12)：98-101.

[3] 刘 军.基于虚拟力算法的 WMSNs覆盖研究[J].传感器与微系统,2016,35(11):74-76.

[5] Khoufi I,Minet P,Laouiti A.OA-DVFA:A distributed virtual forces-based algorithm to monitor an area with unknown obstacle-s[C]∥IEEE Consumer Communications & Networking Confe-rence,IEEE,2016:1036-1041.

[6] Li Y,Zhang B,Chai S.An energy balanced-virtual force algo-rithm for Mobile-WSNs[C]∥IEEE International Conference on Mechatronics and Automation,IEEE,2015:1779-1784.

[7] 覃景繁,欧阳景正.一种新的变步长LMS自应用滤波算法[J].数据采集与处理,1997,12(3):171-174.

[8] Zou Y,Chakrabarty K.Sensor deployment and target localization based on virtual forces[C]∥The Twenty-Second Annual Joint Conference of the IEEE Computer and Communications,INFOCOM 2003,IEEE Societies,IEEE,2003:1293-1303.

[9] 张 涛,余翔宇,蓝俊健,等.改进的无线传感器网络节点虚拟力部署方法[J].计算机应用研究,2015,32(11):3356-3358.

[10] 孟小猛. 自适应滤波算法研究及应用[D].北京:北京邮电大学,2010.