整形为平顶洛伦兹光束的非球面透镜组研究
钟旭森,唐晓军,王 钢
(华北光电技术研究所,北京 100015)
1 引 言
激光器输出的光束通常为高斯光束,而在激光的实际应用中,例如激光驱动核聚变、激光材料加工、激光医疗等领域,平顶光束相比于高斯光束具有更好的应用效果[1]。将高斯光束整形为平顶光束方法很多,利用非球面透镜组、全息滤波器、二元光学元件(BOE)、微透镜阵列整形、双折射透镜组、液晶空间光调制器、长焦深整形元件(圆锥镜光束变换)等方法均能实现[2-3]。
1965年,Frieden提出了基于相位移动的非球面透镜组整形方法,经过Kreuzer等人的研究[4-5],得到非球面透镜组面型求解方法,随着非球面透镜加工及检测技术的发展,该整形方案已向实用化迈进。 本文利用平顶洛伦兹函数表示整形后的平顶光束分布,分析该方法应用于高斯光束转变为平顶光束中的可行性以及各参数对结果的影响。
2 非球面透镜组整形原理
非球面透镜组由两个非球面透镜组成,共有两种结构,一种是开普勒型,另一种是伽利略型,本文中采用伽利略型非球面透镜组。如图1所示,波长为λ的输入光束与输出光束关于光轴对称,光轴沿z方向,两面非球面在垂轴截面平面坐标分别为r、R,d是两个非球面的距离,n是透镜组的折射率,输入和输出光束在两个截面上的光强分布分别为f(r)、I(R)。由能量守恒定律,光强分布归一化后可得[6-7]
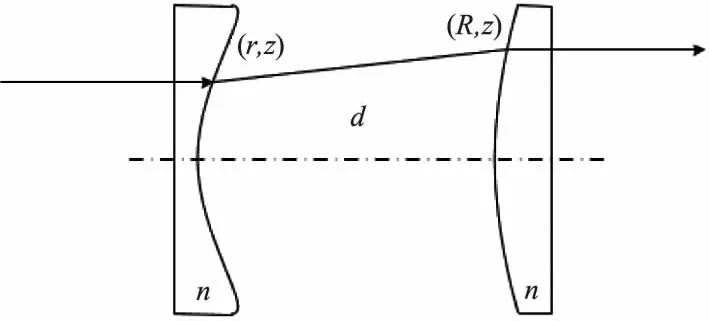
图1 伽利略型非球面透镜组结构示意图Fig.1 Galilean configruration aspheric lens group structure diagram

(1)
输入的高斯光束的光强分布表示为:
(2)
式中,ω0是高斯光束束腰半径。
输出平顶光束考虑到数值可积分性,使用平顶洛伦兹函数表示光强分布描述光强分布,表示为:
(3)
式中,R0为平顶光束半高宽;q为平顶洛伦兹函数阶数。
根据能量守恒定律,两个光强分布关系有:
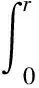
(4)
将式(2)与式(3)代入上式,可以得到微分方程:
(5)
解此微分方程可得到两个非球面坐标r与R之间的关系,即映射函数,得:
(6)
化简后:
(7)
求式(7)的反函数可以得到:
(8)
根据光线追踪函数式(9)、(10)[8]:
(9)
(10)
将映射函数代入其中可得到两个非球面透镜的数值解。
3 整形系统参数分析
由输入输出光束的光强分布函数,束腰半径、透镜折射率、透镜间距、阶数与平顶光束半高宽决定整个整形系统的设计与计算,高斯光束束腰半径、透镜折射率和间距在系统整体设计相对固定,为此,主要考虑匀化洛伦兹函数阶数和半高宽的影响。
3.1 阶数q值对平顶光束的形状及映射函数的影响
利用公式(3),画出不同q值的平顶光束分布图形,如图2所示。
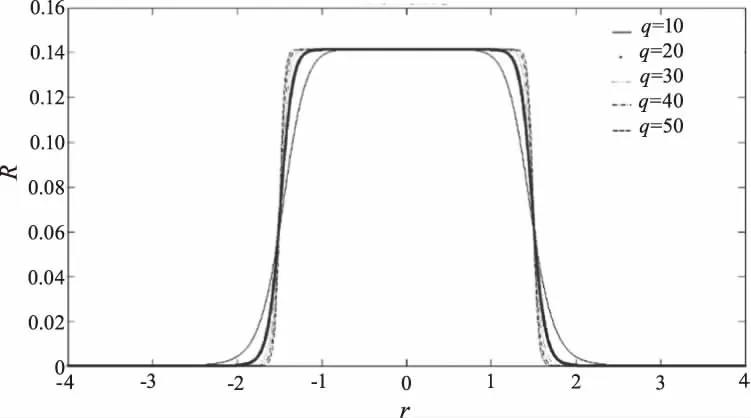
图2 不同q时的平顶光束形状(R0==1.5)Fig.2 The shape of the flat beam at different q values
可以看出随着阶数的变大,中心区域一定范围内光束强度呈均匀分布,边缘部分逐渐陡峭,图形向理想平顶光束变化;当阶数为20或往上增长,图形变化逐渐变小。
同样,根据公式(7)画出不同q值的映射函数图形,见图3。
选取半高宽为3,随着r的增大,因为平顶光束光强分布比较集中,映射函数图形应尽可能的趋于平缓,能达到更高的光能利用率,由图3所示,当阶数大于20时,映射函数也逐渐趋于平缓,但变化也同时变小。 另外,q值越大,将会到影响后续计算的精度。综合上述两点的讨论,本论文中选用25为平顶洛伦兹光束的阶数。
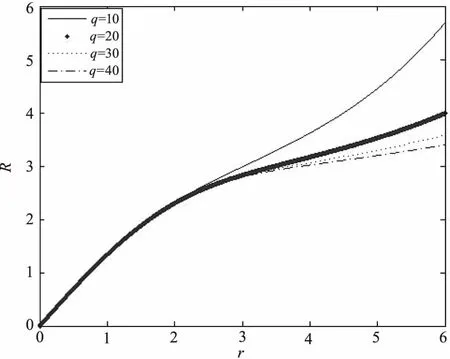
图3 不同q值时映射函数(ω0=3;R0=3)Fig.3 Mapping functions with different q values(ω0=3;R0=3)
3.2 半高宽对两片伽利略型非球镜面型的影响
图4表示伽利略型非球面透镜组的两个面型,从图中显示第一片透镜z值比第二片透镜小一倍。

图4 两片非球面透镜的面型曲线Fig.4 The profile of two aspherical lenses
可知,对于两片透镜,随着半高宽的增加,中心曲率变大,而半高宽过小的时候,中心区域接近平面。半高宽较大时,两个非球面面型在边缘区域也相较平缓,为此,在数值拟合非球面的面型精度和非球面加工精度一定的情况下,设计时半高宽不宜过小。
4非球面透镜截面拟合及ZEMAX模拟仿真分析
通过MATLAB软件,计算出非球面面型的数值解,并采用偶次非球面拟合两片透镜,非球面表达式如下:
(11)
使用最小二乘法进行曲线拟合,在保证拟合精度条件下,降低曲线拟合难度,上式中的K、c值均为零;k最高幂次取到5。
非球面整形结构参数如表1所示。

表1 非球面整形结构参数Tab.1 Aspheric shaping parameters
半高宽R0=6,两个非球面系数具体数值依次如表2所示。
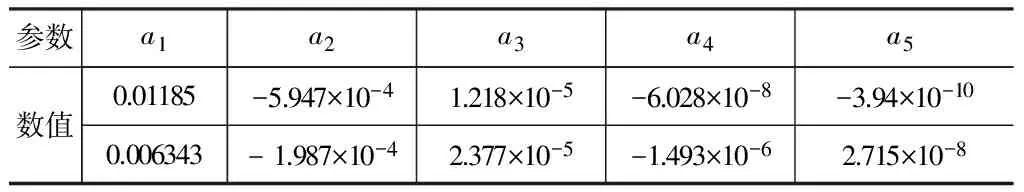
表2 非球面透镜组面型拟合参数Tab.2 Aspheric lens group surface fitting parameters
在ZEMAX软件进行物理光学传播(pop)分析,半高宽取不同值时得到系统结构图以及仿真输出光束图形如图5中(a)、(b)、(c)。
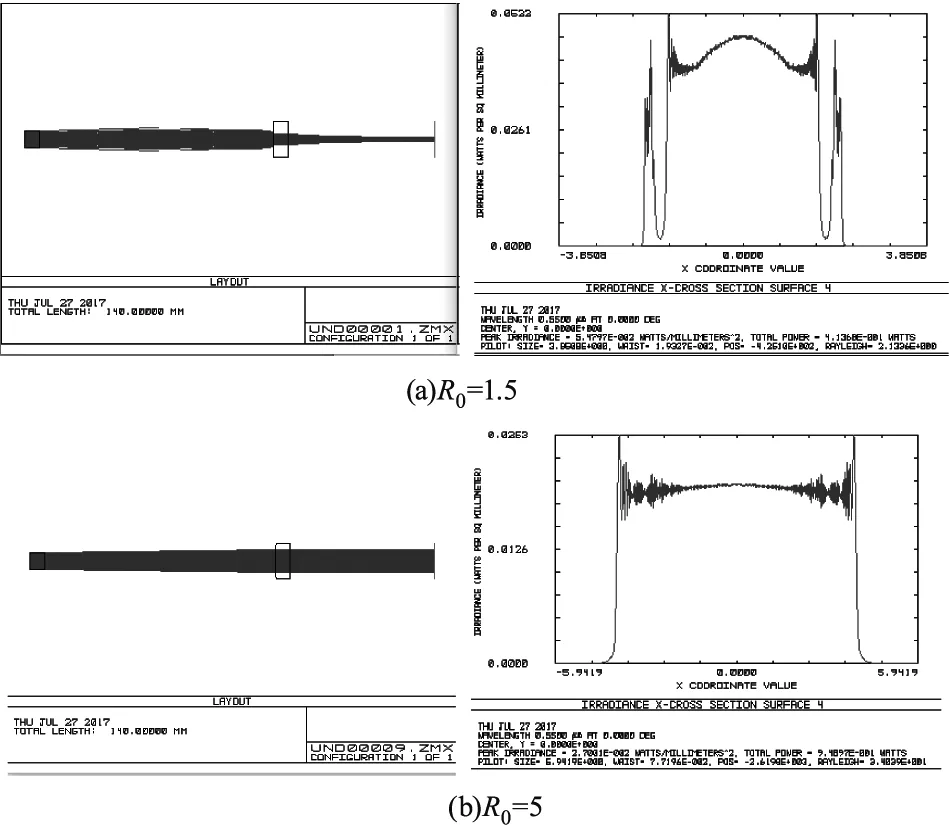

图5 仿真结构图与物理光学分析结果Fig.5 Simulation structure diagram and physical optical analysis results
由图5所示,当半高宽为1.5时,两个透镜面型接近于平面,虽然中心区域半径基本一致,但输出光束不理想,中心部分光强分布不均,仍然突起,且周围有两个旁瓣,从整体结构图可以看出,该旁瓣第一面光束传输到第二面时口径与理想输出口径存在差异导致,光能转化率较低,在后续传播将会影响更大,根本原因在于第一面的面型中心部分曲率过小,受拟合以及加工精度影响较大。
当半高宽为5时,输出光束中心光强相比较下平缓许多,且两侧的旁瓣消失,输出平顶光束半径也与设计值相符。
当半宽高为6时,中心区域光束光强分布变得十分均匀,基本达到实际需求,边缘尖峰仍受面型精度和平顶洛伦兹函数边缘陡峭性质的影响,但误差也已经在可接受的范围内,输出平顶光束相位也达到要求,能在一定范围内实现稳定传输。由此得到,当使用该非球面透镜对高斯光束进行整形时,适当增大输出光束半径能显著提高系统的整形效果,以获得均匀度较高的平顶光束。
5 结 论
利用伽利略型非球面透镜组,将高斯光束整形后输出平顶光束,使用匀化洛伦兹函数来描述平顶光,推导并计算映射函数和两片非球面透镜的面型,主要通过分析平顶洛伦兹阶数对平顶光分布以及映射函数的影响,阶数为25时能达到整形和计算精度的要求;最小二乘法拟合面型曲线,高斯光束腰半径ω0=3的条件下,在ZEMAX软件中的模拟仿真后,结果说明:随着半高宽的增加,面型曲线更加平滑,也更加便于实际的非球面加工,半高宽R0=6,得到输出十分接近匀化洛伦兹函数的平顶光束。当非球面透镜组起到扩束作用时,可达到较好的整形效果。
参考文献:
[1] Dickey F M,Holswade S C,Shealy D L.Laser beam shaping applications[J].Crc Press,2005.
[2] GONG Huaping,LU Zhiwei,LIN Dianyang.Present status of laser beam spatial shaping[J].Laser & Optoelectronics Progress,2005,42(9):2-5.(in Chinese)
龚华平,吕志伟,林殿阳.激光束空间整形的研究现状[J].激光与光电子学进展,2005,42(9):2-5.
[3] HUANG Shan,DENG Leimin,YANG Huan,DUAN Jun.Homogenization design of laser diode based on ZEMAX[J].Laser Technology,2014,38(4):522-526.(in Chinese)
黄珊,邓磊敏,杨焕,等.基于 ZEMAX 的半导体激光器匀光设计[J].激光技术,2014,38(4):522-526.
[4] Frieden B R.Lossless conversion of a plane laser wave to a plane wave of uniform irradiance[J].Applied Optics,1965,4(11):1400-1403.
[5] GAO Yuhan.Research of gaussian beam shaping[D].Changchun:Changchun University of Science and Technology,2012.(in Chinese)
高瑀含.高斯光束整形技术研究[D].长春:长春理工大学,2012.
[6] CHEN Kai,LI Pingxue,CHEN Meng,et al.Design and analysis of surface parameters of aspheric lenses system converting gaussian beam to flattop beam[J].Laser & Optoelectronics Progress,2011,48(3):50-54.(in Chinese)
陈凯,李平雪,陈檬,等.高斯光束整形为平顶光束的非球面镜系统设计和面形参数分析[J].激光与光电子学进展,2011,48(3):50-54.
[7] GAO Yuhan,AN Zhiyong,LI Nana,et al.Optical design of Gaussian beam shaping[J].Optics and Precision Engineering,2011,19(7):1464-1471.(in Chinese)
高蠫含,安志勇,李娜娜,等.高斯光束整形系统的光学设计[J].光学 精密工程,2011,19(7):1464-1471.
[8] FAN Zengming,LI Zhuo,QIAN Lixun.Aspherical lens laser beam shaping system[J].Infrared and Laser Engineering,2012,41(2):353-357.(in Chinese)
范增明,李卓,钱丽勋.非球面透镜组激光光束整形系统[J].红外与激光工程,2012,41(2):353-357.

