距离多普勒耦合对雷达滤波精度影响分析∗

李国君 赵栋华 赵永铁

（中国人民解放军92941部队 葫芦岛 125001）

1 引言

雷达系统作为现代导弹武器系统重要前端，具有感知目标的关键作用，是武器系统的“千里眼”和“顺风耳”。现代战争条件下，要求雷达既要看得远又要看得准，雷达看得远要求发射信号为宽脉冲，宽脉冲在提高雷达威力的同时将带来雷达分辨率下降的负面影响，为解决雷达威力与分辨率的矛盾，现代雷达系统多采用脉冲压缩技术。线性调频脉冲压缩体制具有对多普勒频移不敏感［1］的特点，即相对固定载频而言，目标回波载频的变化是多普勒频移和线性调频本身变化量双重作用的结果。因此线性调频脉冲压缩信号在雷达信号中应用最广泛，但引入的问题是匹配滤波器输出响应将出现与多普勒频移成正比的附加延时，即距离多普勒耦合现象［2］。

本文主要研究在雷达数据处理阶段，距离多普勒耦合对雷达滤波的影响，主要研究对滤波数学模型、滤波精度等方面影响问题。

2 距离多普勒耦合系数

雷达发射电磁波被目标散射后，由接收天线进行接收，并经两次变频至中频后进行信号检测，目前通常的信号检测方法是利用匹配滤波器完成信号检测［3］。线性调频信号是载频为线性变化矩形脉冲。若脉冲宽度为τ0，载波中心频率为f0，频率从f1变化至f2，则匹配滤波器的时延输出为频率的线性函数，可表示为

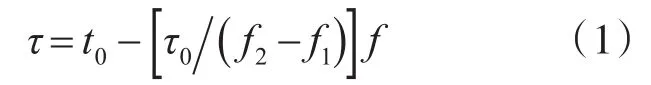
其中，t0为匹配滤波器的固有时延。

由于多普勒频移的影响，在匹配滤波器的输出响应中，增加了多普勒频移的输出，即

v为目标运动径向速度。

由此引入的时延为

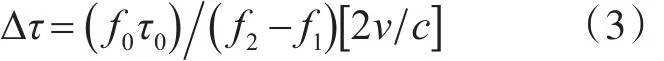
令

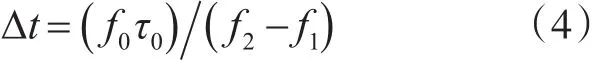
Δt为描述距离多普勒耦合程度的参数，称之为距离多普勒耦合系数［4～6］。

3 考虑耦合效应的雷达滤波过程

当目标散射回波信号经匹配滤波器检波并经门限检波后，得到目标的距离信息，同时经单脉冲测角得到目标的角度信息，距离微分或多普勒滤波后得到目标的速度信息。在得到目标的四维信息后，雷达数据处理完成目标航迹起始、航迹相关［7］并在雷达显示终端上进行显示［8～9］。根据信号处理速度要求，目标航迹数据预测、相关和外推等算法目前多可采用Kalman滤波、α-β-γ滤波或综合采用上述两种滤波方法。

本文从α-β-γ滤波入手分析距离多普勒耦合效应对滤波的影响。Kalman滤波与α-β-γ滤波的主要区别其滤波增益矩阵是时变的，其它滤波过程均相同［10～11］，距离多普勒耦合对α-β-γ滤波影响的分析方法适用于对Kalman滤波影响分析。

3.1 α-β-γ滤波

α-β-γ滤波器用于对匀加速目标的跟踪，系统状态方程［4～5］为

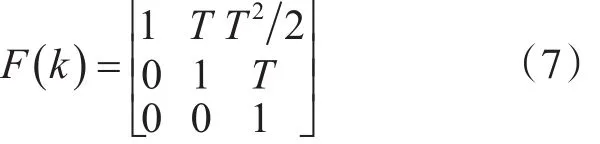
其中：T为采样间隔。

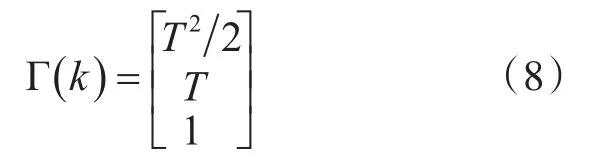
系统量测方程为

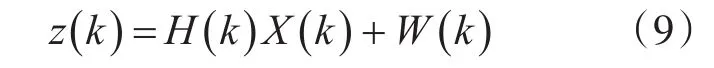
量测矩阵H为

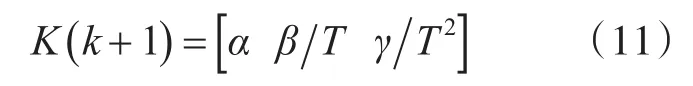
其中，工程上α、β和γ一般采用经验参数值，本文采用多项式拟合方法［12］确定滤波增益参数值，即

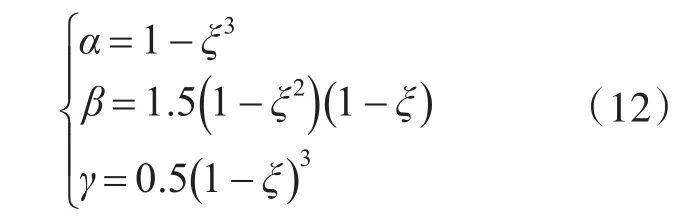
其中：0＜ξ＜1。

在实际工程应用中，对于不同的状态噪声和量测噪声，ξ取值不同有可能导致滤波发散。

3.2 考虑距离多普勒耦合的α-β-γ滤波

当存在距离多普勒耦合时，α-β-γ滤波器量测矩阵H变为H′，其形式为

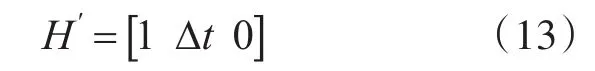
Δt即为式（4）中距离多普勒耦合系数。α-β-γ滤波器的其它数学模型均不变。

为分析距离多普勒耦合对α-β-γ滤波的影响，引入距离、速度和加速度的均方根误差Δ，其数学形式为

其中：N为Monte-Carlo仿真次数，为k时刻目标状态（距离、速度和加速度）真实值（根据状态方程得出），为目标状态滤波估计值［13］。

4 仿真分析

4.1 仿真条件

假设某型雷达发射脉冲载频f0=5GHz，脉冲宽度分别为τ0=10、40 μs，调频带宽B=1MHz，则距离多普勒耦合系数Δt分别为0.05和0.2。为评估距离多普勒耦合对滤波估计的影响，采用2000次Monte-Carlo仿真分析，状态噪声方差，量测噪声方差。为保证α-β-γ滤波器收敛速度和跟踪精度，在给定上述状态噪声和量测噪声情况下，ξ取值为0.5。

假设目标沿雷达径向作匀速直线运动，目标初始状态值为距离100km、速度200m/s、加速度0.5m/s2。目标持续运动时间为100s，采样间隔为1s，初始估计值取第一次量测值。当采用本文的滤波精度分析方法时，目标初始状态值对仿真结果分析没有影响，因此目标初始状态值可根据实际情况灵活选取。

图3～5分别为距离多普勒耦合系数Δt分别为0、0.05和0.2时，kalman滤波器输出的距离、速度和加速度滤波均方根误差。

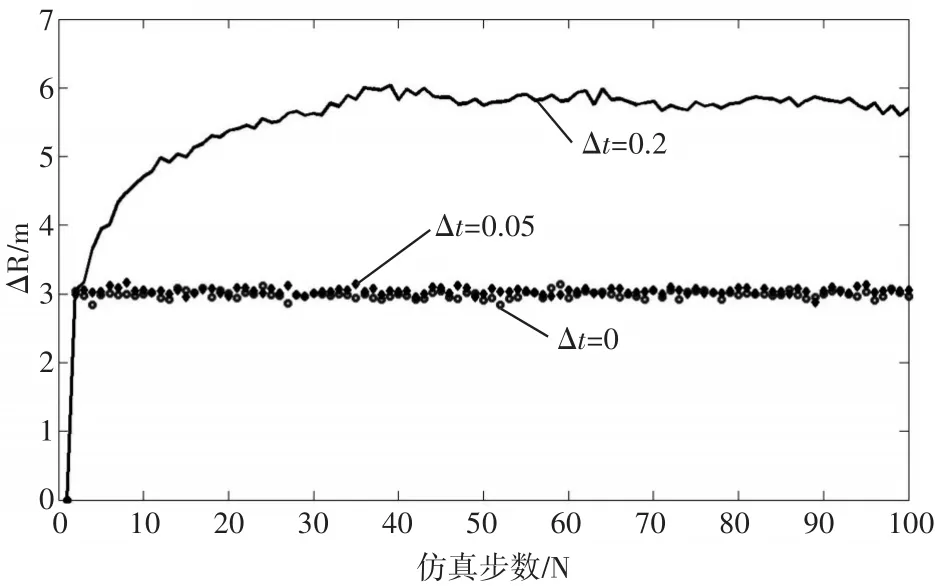
图3 距离均方根误差

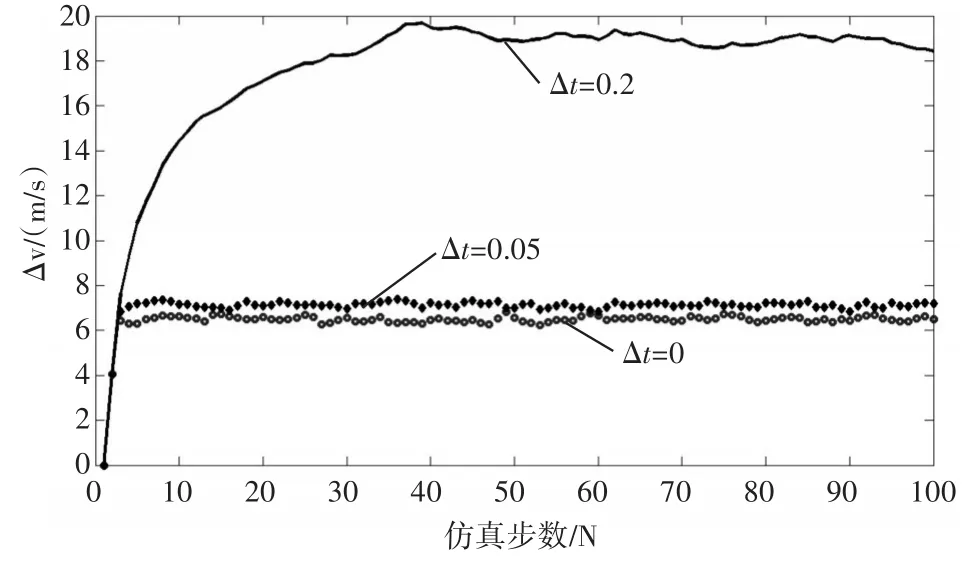
图4 速度均方根误差

图5 加速度均方根误差

4.2 仿真结果分析

根据仿真结果，可得出如下结论：

1）在系统状态噪声和量测噪声一定的情况下，在距离多普勒耦合系数分别为0和0.05时，α-β-γ滤波器滤波精度会发生微小的变化，很多情况下可以忽略。

2）距离多普勒耦合系数对α-β-γ滤波影响存在一临界点，当耦合系数大于该临界点时，滤波精度精度（距离、速度和加速度）急剧变差，在图3～5中，距离多普勒耦合系数取0.2时，α-β-γ滤波器滤波精度急剧变差，该系数进一步增大时，微小的耦合系数增量将导致滤波迅速发散。

3）为避免距离多普勒耦合对雷达数据处理的影响，根据距离多普勒耦合数学模型，按照目前电子器件发展水平，比较可行的技术手段是增大线性调频信号带宽。

5 结语

距离多普勒耦合是线性调频信号经匹配滤波的固有产物，本文从α-β-γ滤波器出发，研究了该问题对雷达数据处理过程中滤波精度的影响，该问题分析思路具有通用性，经适当修正后适用于绝大多数滤波算法。同时需要指出的是距离多普勒耦合对雷达信号处理同样会产生不利影响，如直升机螺旋桨、喷气式飞机发动机叶片等均会产生距离多普勒耦合，造成目标回波信号包络畸变［14］，因此本文分析的距离多普勒耦合效应具有重要的工程意义。

［1］胡红军.脉冲压缩雷达距离多普勒耦合对测距影响分析［J］.现代雷达，2011，33（12）：47-50.

［2］王元恺，肖泽龙，许建中，等.一种改进的FMCW雷达线性调频序列波形［J］.电子学报，2017，45（6）：1288-1293.

［3］朱文涛，苏涛，杨涛，等.线性调频连续波信号检测与参数估计算法［J］.电子与信息学报，2014，36（3）：552-558.

［4］赵锋，王雪松，肖顺平.高耦合系数条件下径向速度测量的新方法［J］.信号处理，2008，24（3）：460-463.

［5］ROBERT.Effects of Range-Doppler Coupling on Chirp Radar Tracking Accuracy［J］.IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS，1974，10（4）：528-532.

［6］Trofimenko.Influence of range-Doppler coupling on the tracking stability of reentering space objects［C］//2015 In⁃ternational Conference on Engineering and Telecommuni⁃cation，41-44.

［7］郑啸宇，王建卫.基于LFM的双波段雷达航迹起始方法［J］.现代雷达，2016，38（8）：54-58.

［8］左现刚，武变霞，王建平，等.一种改进的基于交互式模型的机动目标跟踪算法［J］.火力与指挥控制，2016，41（11）：41-44.

［9］瞿冬霞.LFM脉冲雷达回波模拟和处理的研究［D］.南京：南京理工大学，2010.

［10］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京：电子工业出版社，2006.

［11］贺若飞，田雪涛，刘宏娟，等.基于蒙特卡罗卡尔曼滤波的无人机目标定位方法［J］.西北工业大学学报，2017，35（3）：435-441.

［12］崔嵬，朱新国，沈清.一种新的三阶距离跟踪环参数设计算法［J］.兵工学报，2010，31（6）：807-810.

［13］杨永建，樊晓光，王晟达，等.基于修正卡尔曼滤波的目标跟踪［J］.系统工程与电子技术，2014，36（5）：846-851.

［14］D.C.Ross，J.L.Vo lakis and H.T.Anastassiu Effi⁃cient Computation of Radar Scattering Modulating from Jet Engines［J］.Radio Science，1996，4：991-997.