一种基于轨道根数约束的最优制导方法
李超兵,吕春红,尚腾
北京航天自动控制研究所,北京 100854
在空间航天器为完成预定任务,需要通过变轨控制来实现不同轨道之间的转移,而为确保航天器能够到达目标轨道,同时节省变轨控制的燃料消耗,需要利用最优控制原理设计制导算法。
以迭代制导为代表的最优制导算法自应用于美国的土星五号运载器以来,逐渐为许多航天器所采纳[1-3]。针对航天器主发动机推力大小不可调的情况,传统迭代制导通常以2个方向的位置和3个方向的速度作为5个终端约束,假设控制角指令由速度约束和位置约束两部分组成,并且位置约束部分为小量[4-7],这样可以首先求解满足速度约束部分的控制角,然后利用小角度近似求解满足位置约束部分的控制角。但这一假设并无严格的理论支撑,且在某些变轨情形下这一假设不再成立,从而限制了传统迭代制导的进一步应用[8-11]。
针对传统迭代制导的不足,研究人员从不同的角度进行了改进研究。陈新民和余梦伦[12]针对运载火箭多级飞行的特点,在传统单级迭代制导方程的基础上,进一步推导了多级迭代制导方程;茹家欣[13]利用最优控制原理,从火箭简化运动方程出发,以火箭推力方向的3分量为控制变量推导了迭代制导方法;池贤彬等[14]利用凸优化技术简化航天器的相对运动动力学模型,并通过迭代制导获得追踪航天器的制导策略。
进一步,在控制对象的模型复杂性和最优控制必要条件的推导方式等方面,现有文献也进行了改进研究。Lu等[15]结合最优控制原理和多级打靶法推导了运载火箭的多级点火制导算法;针对大气层内火箭受力的复杂情况,Lu在文献[16,17]中进一步推导了多级点火制导算法;傅瑜等[18]通过计算终端约束对协态变量的雅克比矩阵,获得了解析求解约束方程的迭代制导方法;郑旭等[19]推导了火箭在大气层外的解析动力学模型,将共轭状态向量和飞行时间作为迭代变量,给出了多终端约束下的迭代制导算法;邓逸凡等[20]研究了适用于航天器空间变轨任务的迭代制导算法,直接以轨道根数为终端约束条件建立边界条件;李超兵等[21]在入轨点轨道坐标系下对制导的开关机点优化,进一步得到改进的迭代制导方法。
现有文献虽然从制导适应性上对传统迭代制导作出了种种改进,但很少直接从轨道根数的约束特性出发对制导算法进行设计,从而难以应用于航天器空间变轨的一般情形。如文献[17,18]以位置速度大小、飞行路径角为终端约束;文献[19,21]以位置和速度分量为终端约束;文献[20]虽然直接针对轨道根数约束,但对乘子变量的消去处理方式复杂,不够直观,且没有给出一般椭圆轨道情形下的约束方程形式。
考虑到上述文献的不足,本文从对地心惯性坐标系下航天器的运动模型出发,利用最优控制原理得到位置速度与协态变量初值的关系式;进一步,针对轨道根数特性,推导了除真近点角外的5个轨道根数约束方程,并利用终端约束中位置速度和轨道根数的关系,以及协态变量的尺度特性得到另外两个约束方程。通过直接求解7个完整约束方程组获得协态变量初值,进而得到最优推力方向。仿真结果表明了所提制导方法的有效性。
1 最优制导问题描述
考虑有限推力大小的情形,在地心惯性坐标系下,航天器的运动模型为

(1)
式中:r为位置;V为速度;g(r)为r处的地球引力加速度矢量;T为发动机推力大小;1T为单位矢量,表示发动机推力方向;m为航天器质量;g0为在参考半径R0(可取地球椭球模型的长半轴)处的标准重力加速度;Isp为发动机比冲(采用重量描述,单位为s)。
考虑到发动机点火持续时间通常在几百秒以内,航天器的运动量在整个轨道变化范围内可以看作小量,因此g(r)可采用式(2)近似:
(2)
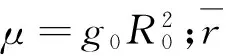
(3)

(4)

制导的终端约束通常由关于终端位置rf和终端速度Vf的k(k≤6)个等式约束组成:
φ(rf,Vf)=0
(5)
为节省燃料,推力方向1T可通过求解使得下面指标最小的最优控制问题来获得:
(6)
注意式(6)中以当前瞬时时刻为0时刻;τf=tf/tref,tf为终端时刻。整个制导的思路是:在每一个制导解算周期内,通过迭代求解式(3)~式(6)组成的最优控制问题来获得最优推力方向1T,随着飞行时间的增加,实际位置与终端约束的位置越来越靠近,因此对引力加速度的近似误差也会越来越小。
根据最优控制理论,选择如下哈密顿函数:
H0+TF
(7)
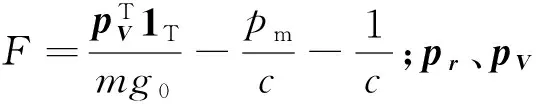
(8)
注意式(8)中的求导运算同样是相对于无量纲化时间τ而言的。

设pr的初值为pr0,当前瞬时时刻的位置和速度分别为r0和V0,根据式(8)有
(9)
式(9)为关于pV和-pr/ω的线性微分方程,其解为
(10)
将式(10)进一步展开可得
(11)
根据式(3)有
(12)
定义
(13)
(14)
式中:
则式(12)的解可写为
(15)
根据数值积分公式,有
(16)
(17)
式中:各ic和is的值均可根据式(11)来确定。因此有

(18)
V(τ)=-ωsin(ωτ)r0+cos(ωτ)V0+cos(ωτ)·

(19)
可见,在当前瞬时时刻位置和速度确定的前提下,pr(τ)、pV(τ)、r(τ)和V(τ)均为协态变量初值pr0和pV0的函数,而实际最终的位置和速度还取决于τf,一共有7个未知变量,如果能够构造关于pr0、pV0和τf的7个方程,则求解这个方程就能获得pV0,从而得到最优推力方向。
2 约束方程构造
在发动机推力大小T不可调的前提下,理论上只能满足5个终端约束,对于航天器入轨来说,通常选取轨道根数来描述入轨条件,形成以轨道根数描述的终端约束条件。经典的6个轨道根数为半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角w、真近点角f,对应的目标量均用下角标T表示,通常不约束真近点角,即选取的5个终端约束为半长轴aT、偏心率eT、轨道倾角iT、升交点赤经ΩT和近地点幅角wT。
2.1 半长轴约束
由二体问题中的活力公式可知
(20)

(21)
因此,半长轴的终端约束为
(22)
2.2 偏心率约束
φ2(rf,Vf)=
(23)
2.3 轨道倾角约束
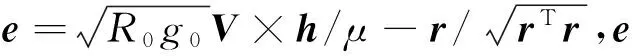
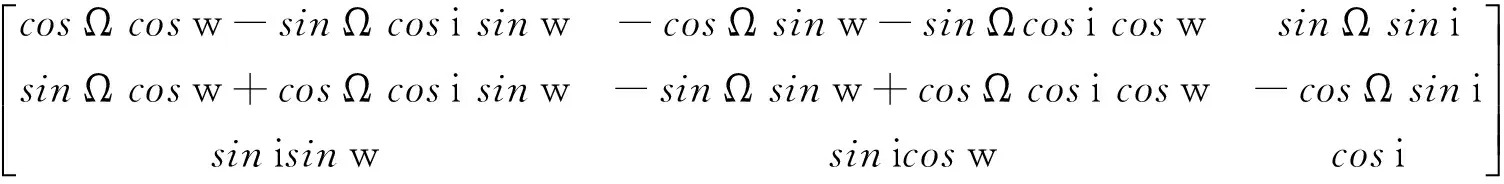
(24)
显然,在惯性系中h方向的单位矢量为
(25)
(26)

2.4 升交点赤经约束
根据2.3小节中的分析,升交点赤经约束为
(27)
2.5 近地点幅角约束
偏心率矢量e在地心惯性坐标系中的分量满足:
(28)
从而有
(29)
(30)
从而有
(31)
结合式(28)、式(29)和式(31)可知,近地点幅角约束为
(32)
式中:
φ1~φ5构成了关于rf和Vf的5个终端约束,为求解协态变量初值和飞行时间,还需要2个终端约束构成完整的约束方程。
2.6 第6个约束方程
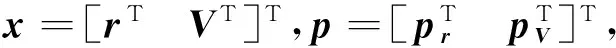
(33)
式中:zp为拉格朗日乘子向量,为避免数值求解困难,需要消去zp。通常的方法是求解下述方程:
(34)
得到关于rf和Vf的解y,则有
yTpf=0
(35)
式(35)构成了第6个约束方程。
上述方法虽然直观,但是实际求解式(34),特别是获得y的解析表达式并不容易,因此这里考虑另外一种思路。
由于位置速度和6个轨道根数之间可以互相转换,rf和Vf可以表示为轨道根数的形式,因此φ1~φ5也可以表示成轨道根数的函数,即令η=[aeiΩwf]T,则终端约束可写为
(36)

(37)
令y=∂xf/∂ff,则由式(35)可知第6个约束方程为
(38)
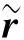
(39)

(40)
(41)
对式(39)微分可得
(42)

(43)

(44)

(45)
(46)
从而可知
(47)
比较式(43)和式(47)可得
(48)

(49)
进一步考虑无量纲位置和速度的情形,由式(48)和式(49)可得
(50)
(51)
因此有
(52)
从而式(38)可写为
(53)
式(53)即为第6个约束方程。
2.7 第7个约束方程
由最优控制原理,协态方程可写为
(54)
(55)
可见,哈密顿函数也只是每一项进行了同样的缩放,因此不会影响最优推力方向的求解。因此,这里考虑针对协态变量的尺度设计第7个约束方程如下(选择不唯一):
(56)

注:在获得7个完整约束方程后,在每一次制导计算周期内利用牛顿迭代法对方程进行求解获得协态变量初值,即可得到最优推力方向。在仿真程序中,牛顿迭代法求解方程组所需要的雅可比矩阵利用数值分析中常用的差商法获得,因此计算量要大于传统的迭代制导方法。与迭代制导类似,在一开始的几次制导计算周期内需要的迭代次数较多,后面基本迭代1~2次即可得到解。对于第3节仿真中的例子,在箭载计算机运行中程序时,完成一次制导指令解算所需的时间大约为5 ms。
3 仿真验证
为验证所提方法的有效性,针对航天器某一次变轨任务进行仿真验证。设置航天器的初始质量为8 680.554 8 kg,主发动机推力的大小为6 500 N,比冲为3 095 m/s,初始和目标轨道根数如表1所示。
假设航天器的初始姿态已经调整到合适位置,从初始位置开始即进行制导解算,不考虑前段累积偏差。仿真计算步长选为10 ms,考虑J2引力摄动项,终止姿态角迭代计算的条件选为剩余分析时间小于 5 s 时,关机条件为剩余飞行时间小于0.1 s时。

表1 航天器的初始和目标轨道根数Table 1 Initial and target orbital elements of spacecraft
针对表1中的数据,将本文方法与文献[20]中方法进行对比仿真,制导结果如图1所示,本文方法的实际飞行时间为168.130 0 s,文献[20]中方法的实际飞行时间为168.670 0 s。
由图1中的仿真结果可以看出,在整个制导过程中,两种方法均能保证剩余时间逐渐减小到0,除真近点角外的5个轨道根数误差最终也趋于0,制导结束后的偏差数据如表2所示。
由表2可知,2种方法均能保证航天器最终到达的轨道与目标轨道根数的偏差在容许范围内,且与文献[20]中方法相比,本文方法的轨道根数偏差更小,如果需要进一步减小某个轨道根数偏差,可对该轨道根数的约束方程进一步进行加权,如若需要进一步减小偏心率偏差,则可根据式(23),在程序中令φ2=γφ2,γ为大于1的数,如取为10、100等。
进一步,假设推力和比冲等各偏差均服从正态分布,对应的3σ偏差值如表3所示。进行1 000次打靶仿真,最终得到的轨道根数偏差如图2所示。

图1 本文方法和文献[20]中方法的制导结果仿真对比Fig.1 Simulation comparion of guidance results between proposed method and method in Ref.[20]

方法半长轴偏差/m偏心率偏差轨道倾角偏差/(°)升交点赤径偏差/(°)近地点幅角偏差/(°)本文方法-22.0731-9.7929×10-5-4.9592×10-52.7294×10-51.5200×10-2文献[20]方法345.3752-1.7219×10-4-7.6690×10-52.0290×10-42.2500×10-2

表3 误差参数3σ偏差值Table 3 3σ deviation values of error parameters
从图2可以看出,对于表3中的误差条件,半长轴偏差最大为200 m,偏心率偏差最大为8.0×10-4,轨道倾角和升交点赤经偏差最大为4×10-4(°),近地点幅角偏差最大为0.15°。此外,各轨道根数偏差参数均集中在零附近,仿真结果表明本文所提制导算法对于偏差具有一定的适应性。

图2 轨道根数统计偏差Fig.2 Statistical error of orbital element
4 结 论
本文直接从地心惯性坐标系下航天器的运动模型出发,将制导指令求解问题转化为约束方程组的构造与求解问题,并进行了相应的仿真分析。
1) 不需要假设制导指令角的形式,适用范围大于传统的迭代制导。
2) 从最优控制理论出发求解制导指令,具有一定的最优性。
3) 所提方法能够保证航天器最终到达的轨道与目标轨道根数的偏差在容许范围内,且对于偏差具有一定的适应性。
[1] CHEN S Y, XIA Q L. A Multiconstrained ascent guidance method for solid rocket-powered launch vehicles[J]. International Journal of Aerospace Engineering, 2016(1):1-11.
[2] QUADRELLI M B, WOOD L J, RIEDEL J E, et al. Guidance, navigation, and control technology assessment for future planetary science missions[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(7): 1165-1186.
[3] VACHON A, DESBIENS A, GAGNON E, et al. Launch ascent guidance by discrete multi-model predictive control[J]. Acta Astronautica, 2014, 95: 101-110.
[4] HULL D G, HARRIS M W. Optimal solutions for quasiplanar ascent over a spherical Moon[J]. Journal of Guidance, Control and Dynamics, 2012, 35(4): 1218-1223.
[5] LU P, FORBES S, BALDWIN M. A versatile powered guidance algorithm[C]∥AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2012: 4843-4858.
[6] JEB S O, JOHN H W, TANNEN S V, et al. Space launch system ascent flight dontrol design[DB/OL].http:∥ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140008731.pdf.
[7] LAN X J, LIU L, WANG Y J. Online trajectory planning and guidance for reusable launch vehicles in the terminal area[J]. Acta Astronautica, 2016, 118: 237-245.
[8] HALBE O, RAJA R G, PADHI R. Robust reentry guidance of a reusable launch vehicle using model predictive static programming[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(1): 134-148.
[9] SONG E J, CHO S, ROH W R. A comparison of iterative explicit guidance algorithms for space launch vehicles[J]. Advances in Space Research, 2015, 55(1): 463-476.
[10] TIAN B, FAN W, SU R, et al. Real-time trajectory and attitude coordination control for reusable launch vehicle in reentry phase[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1639-1650.
[11] LU B, CUI N, FU Y, et al. Closed-loop atmospheric ascent guidance based on finite element method[J]. Aircraft Engineering and Aerospace Technology: An International Journal, 2015, 87(5): 393-401.
[12] 陈新民, 余梦伦. 迭代制导在运载火箭上的应用研究[J]. 宇航学报, 2003, 24(5): 484-489.
CHEN X M, YU M L. Study of iterative guidance application to launch vehicles [J]. Journal of Astronautics, 2003, 24(5): 484-489 (in Chinese).
[13] 茹家欣. 液体运载火箭的一种迭代制导方法[J]. 中国科学E辑:技术科学, 2009, 39(4): 696-706.
RU J X. An iterative guidance method for liquid launch vehicle[J]. Science in China Series E: Technological Sciences, 2009, 39(4): 696-706 (in Chinese).
[14] 池贤彬, 岳晓奎, 李鹏. 基于凸优化的自主交会迭代制导方法[J]. 中国空间科学技术, 2014(1): 26-34.
CHI X B, YUE X K, LI P, et al. Iterative guidance method of autonomous rendezvous based on convex optimization[J]. Chinese Space Science & Technology, 2014(1): 26-34.
[15] LU P, GRIFFIN B J, DUKEMAN G A, et al. Rapid optimal multiburn ascent planning and guidance[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1656.
[16] LU P, SUN H, TSAI B. Closed-loop endoatmospheric ascent guidance[J]. Journal of Guidance Control and Dynamics, 2003, 26(2): 283-294.
[17] LU P, PAN B. Highly constrained optimal launch ascent guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 404-414.
[18] 傅瑜, 陈功, 卢宝刚,等. 基于最优解析解的运载火箭大气层外自适应迭代制导方法[J]. 航空学报, 2011, 32(9): 1696-1704.
FU Y, CHEN G, LU B G, et al. A vacuum adaptive iterative guidance method of launch vehicle based on optimal analytical solution[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1696-1704 (in Chinese).
[19] 郑旭, 高长生, 陈尔康,等. 一种基于大气层外解析动力学模型的最优迭代制导方法[J]. 西北工业大学学报, 2016, 34(6):1093-1100.
ZHENG X, GAO C S, CHEN E K, et al. An optimal iterative guidance method based on exoatmospheric analytical dynamic model [J]. Journal of Northwestern Polytechnical University, 2016, 34(6): 1093-1100 (in Chinese).
[20] 邓逸凡, 李超兵, 王志刚. 一种基于轨道要素形式终端约束的航天器空间变轨迭代制导算法[J]. 航空学报, 2015, 36(6): 1975-1982.
DENG Y F, LI C B, WANG Z G. An iterative guidance algorithm using orbital elements as terminal constraints for spacecraft orbit transfer [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1975-1982 (in Chinese).
[21] 李超兵, 王晋麟, 李海. 一种基于多终端约束的最优制导方法[J]. 中国空间科学技术, 2016, 36(5): 9-17.
LI C B, WANG J L, LI H. An optimal guidance method based on multiple terminal constraints[J]. Chinese Space Science and Technology, 2016, 36(5): 9-17 (in Chinese).

