输入受限的高超声速飞行器鲁棒反演控制
骆长鑫,张东洋,雷虎民,卜祥伟,叶继坤
1.空军工程大学 研究生院,西安 710051 2.空军工程大学 防空反导学院,西安 710051
吸气式高超声速飞行器(AHV)已成为21世纪世界航空航天技术发展新的制高点,必将在未来国防装备发展和民用空天技术应用中发挥极其重要的战略作用。然而,AHV在动力学特性上表现出比传统飞行器更加显著的强耦合、强非线性、非最小相位行为和模型不确定性,且对飞行姿态异常敏感,这使得AHV的飞行控制成为当今控制领域的前沿问题[1-4]。
因为AHV动力学特性十分复杂且缺少建模所需的实验数据,在现有的国内外研究成果中,大多集中于对AHV纵向运动模型的研究[5],相关的控制工作也在纵向平面内展开。同时,考虑到其对姿态的敏感以及燃料消耗等因素,在飞行任务中,应尽量避免横向机动,因此对其纵向运动进行研究有其合理性和实际意义[6]。
AHV以升降舵作为执行机构来控制纵向运动的高度和姿态,随着飞行高度的增加,升降舵的执行效率会显著下降,例如,AHV以5马赫速度飞行时,在10 km高空处的升降舵执行效率相对100 m处将下降1/3以上[5]。同时,AHV在飞行过程中会受到诸如阵风、湍流以及未知气流的干扰,因此,AHV在高空飞行时极易出现升降舵饱和现象。而一旦执行器达到饱和,理想控制律就无法得到有效的执行,闭环控制系统将不再稳定,极有可能造成控制系统的失效,这就迫切要求开展AHV的抗饱和控制研究。文献[7]只考虑发动机的节流阀饱和现象,提出了一种基于时标分离的神经控制方法。文献[8-9]设计了一种鲁棒控制策略,采用辅助线性矩阵不等式解决了执行器的饱和问题。文献[10]通过一个辅助系统对跟踪误差进行了修正,基于Lyapunov稳定性理论证明了修正误差的有界性,虽然仿真结果表明该方法在处理执行器饱和问题上具有一定的可行性,但无法从理论上保证跟踪误差的有界。文献[11]进一步将文献[10]的方法拓展到控制输入与状态(飞行姿态)都受限的AHV飞行控制中,但在工程实际中,AHV并没有相应的执行机构对飞行姿态进行限制。文献[12]采用多层神经网络逼近控制律的饱和特性,有效地处理了控制输入饱和受限的约束,但是神经网络权值调节参数对模型依赖性强,选取困难。针对AHV弹性体模型的控制输入受限问题,文献[13]引入文献[14]所提出的辅助系统对理想控制律进行了补偿,虽然仿真结果证明了在执行机构饱和时控制方法依然有效,但辅助系统过于复杂。文献[15]提出了一种新型补偿策略,通过设计一种新型辅助系统对理想控制律进行了有界补偿,不仅保证了闭环控制系统的稳定性,而且在理论上确保了跟踪误差的有界性,较文献[16]的补偿策略具有一定的优势,但其对执行机构的速率受限问题未作讨论。基于文献[15]的补偿思想,文献[17]将AHV的高度子系统转化成标准的纯反馈形式,通过设计一种新型高阶辅助系统对理想控制律进行了补偿,保证了所有闭环信号的有界性,仿真结果表明该方法具有一定的可行性与有效性。
上述文献的研究更多地集中在幅值饱和问题上,而未对速率饱和采取任何应对措施,这极有可能导致控制方法在输入幅值和速率均受限的情况下失效。
本文将研究控制输入受限情况下高超声速飞行器弹性体模型的鲁棒反演控制问题。基于辅助误差补偿策略设计反演控制器,保证了执行机构在幅值和速率同时达到饱和时闭环控制系统的稳定性和跟踪误差的有界性。通过引入有限时间收敛微分器(FD),解决了传统反演控制的“微分项膨胀”问题,并在此基础上,设计了一种非线性干扰观测器(NDO),用以精确估计模型的不确定项,进一步提高了控制精度。最后,通过仿真对所设计控制方法的有效性进行了验证。
1 高超声速飞行器运动学模型
美国空军研究实验室的一位学者Parker[18]在Bolender与Doman[19]的研究基础上,建立了AHV纵向运动参数拟合模型:
(1)
(2)
(3)

(4)
(5)
(6)
(7)
式中:
(8)

AHV受力情况如图1所示(G为所受重力),T、D、L、M、N1与N2的参数拟合形式可表示为[18]

图1 AHV模型受力示意图Fig.1 Force map of a AHV model
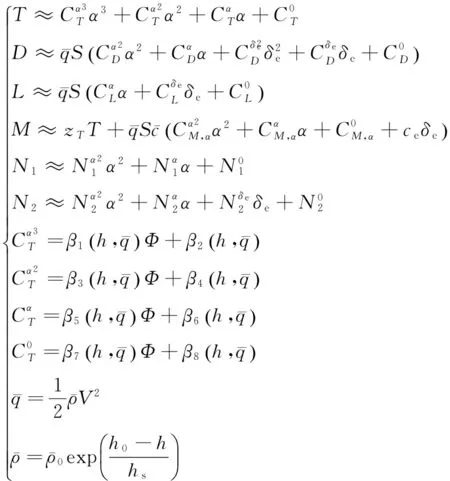
(9)
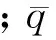
2 控制目标和模型转换
AHV的控制目标是:通过不断调整控制输入Φ和δe,实现飞行器的速度V和飞行高度h对其参考输入Vref和href的鲁棒跟踪,并保持飞行器姿态的稳定和抑制弹性振动。由式(1)~式(5)可以看出,由于Φ直接影响推力,所以速度的变化主要受燃料-空气比Φ控制。高度变化则主要由舵偏角δe控制,这是因为δe直接影响俯仰角速度Q,进而影响俯仰角θ与航迹角γ的变化,最后控制高度h的变化[15,17]。因此,为了便于控制律的设计,通常情况下,在形式上先将AHV模型分解成速度子系统(式(1))和高度子系统(式(2)~式(5)),然后分别对其进行控制律的设计[20-23]。
对于速度子系统,控制目标是设计控制律Φ,实现速度V对其参考输入Vref的稳定跟踪。将速度子系统改写为
(10)
式中:
其中:dV0为外部扰动;ΔfV、ΔgV分别为气动参数摄动量;dV为总不确定项。
对于高度子系统,控制目标是:采用反演控制策略,设计一系列虚拟控制律和最终的实际控制律δe,使得h稳定跟踪href。
将高度跟踪误差定义为
(11)
对式(11)求一阶导数并将式(2)代入可得
(12)
由式(12)可知,将航迹角指令设计为
(13)
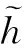
(14)
对式(14)两侧进行拉氏变换,可得其特征方程为
s2+kh1s+kh2=0
(15)
因此,只要保证航迹角γ趋于γcmd,就能实现h对href的稳定跟踪。这样,高度子系统的控制任务就变为确保航迹角γ稳定跟踪γcmd。为了反演控制律设计上的方便,将高度子系统的其他部分(式(3)~式(5))改写为
(16)
式中:
其中:dγ 0和dQ 0为外部扰动;Δgγ、Δfγ、ΔgQ和ΔfQ为气动参数摄动量;dγ与dQ为总不确定项。
注1 由于弹性状态不能被直接测量,并且缺少相应的执行机构对其进行主动抑制,参考文献[13,15]的做法,在式(16)中,把弹性状态视为总不确定项dγ和dQ的一部分。
3 控制器设计
3.1 速度控制器设计
将速度跟踪误差定义为
(17)
对式(17)两侧求一阶导数并将式(10)代入可得
(18)
将控制律Φ设计为
(19)
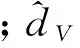
考虑到实际情况中,AHV的执行机构Φ的可执行范围存在一定限度,将其定义为
(20)
式中:Φc为输入受限情况下的理想控制律;Φmin、Φmax分别为Φ的下界与上界。
为保证飞行器执行机构Φ在瞬时饱和的情况下仍能实现对参考输入的稳定跟踪,设计如下辅助系统对控制律Φ(式(19))进行修正。
(21)
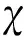
将速度跟踪误差(式(17))修正为
(22)
对式(22)求时间的一阶导数并将式(18)与式(21)代入可得
(23)
将理想控制律Φc修正为
(24)
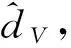
3.2 高度控制器设计
步骤1 将航迹角跟踪误差定义为
(25)
对式(25)求一阶导数并将式(16)代入可得
(26)
将虚拟控制指令θcmd设计成
(27)

步骤2 将俯仰角跟踪误差定义为
(28)
对式(28)求时间的一阶导数并将式(16)代入可得
(29)
将虚拟控制指令Qcmd设计为
(30)
式中:kθ1、kθ2∈R+为待设计参数;θd为θcmd的估计值。
步骤3 将俯仰角速度跟踪误差定义为
(31)
对式(31)求时间的一阶导数并将式(16)代入可得
(32)
将实际控制律δe设计为
δe=
(33)

由于在实际情况中,执行机构δe的幅值和速率均受到一定程度的限制,分别将其定义为
(34)
(35)

考虑δe幅值受限,采用如下辅助系统对控制律δe(式(33))进行修正。
(36)
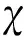
将虚拟控制律(式(30))修正为
(37)
将俯仰角速度跟踪误差(式(31))修正为
(38)
对式(38)求时间的一阶导数并将式(32)与式(36)代入得
(39)
将理想控制律δec设计成
(40)
考虑δe速率受限,采用如下辅助系统对控制律δec进行重设计。
(41)
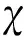
定义舵偏角δe跟踪误差为
(42)
对式(42)求时间的一阶导数可得
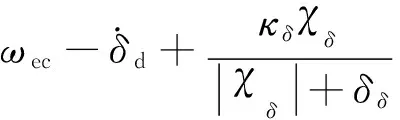
(43)
将控制律ωec设计为
(44)
式中:kδ1、kδ2∈R+为待设计参数;δd为δec的估计值。
而ωe由ωec经过如式(35)所示的约束得到,最终,将控制律δec修正为

(45)
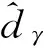
3.3 有限时间收敛微分器设计
定理1 对于如下FD
(46)
式中:R、ai(i=1,2,…,n)∈R+为待设计参数。则存在φ>0与τφ>n使得
(47)
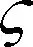
证明:见文献[26],证毕。
采用上述FD分别对γcmd、θcmd、Qcmd、δec的一阶导数进行估计。
(48)
(49)
(50)
(51)
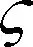
3.4 非线性干扰观测器设计
考虑如下不确定系统

(52)
式中:v∈R为系统状态变量;F(v)与G(v)≠0为连续函数;u∈R为控制输入;d∈R为不确定项。
基于上述FD(取n=2),将NDO设计成如下形式。
定理2 对于如下NDO:
(53)
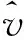
(54)
证明:见文献[25],证毕。
采用上述NDO分别对dV、dγ、dQ进行估计。
(55)

(56)

(57)

3.5 稳定性分析
定理3 针对AHV的速度子系统(式(1)),采用控制律Φc(式(24))、NDO(式(55))和辅助系统(式(36)),则闭环系统局部一致渐进稳定。
证明:定义NDO估计误差为
(58)

将式(24)代入式(23)可得
(59)
选取如下Lyapunov函数:
(60)
对式(60)求时间的一阶导数并将式(59)代入可得
(61)
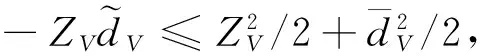
(62)
令kV1>1/2,并定义如下紧集:
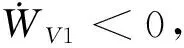
定理4 针对AHV的高度子系统(式(2)~式(5)),采用控制律(式(27)、式(30)、式(40)、式(44)),FD(式(48)~式(51))和NDO(式(56)、式(57)),则闭环控制系统局部一致渐进稳定。
证明:定义NDO估计误差为
(64)
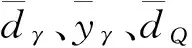
定义FD估计误差为
(65)
将式(31)、式(37)和式(65)代入式(29)可得
(66)
将式(40)、式(64)代入式(39)可得
(67)
将式(44)代入式(43)可得

(68)
选取如下Lyapunov函数:
(69)
对式(71)求时间的一阶导数并将式(26)、式(29)、式(67)和式(68)代入可得


(70)
因为
于是式(70)可写为
(71)

(72)

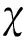
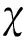
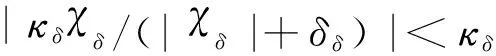
(73)
对式(73)求时间的一阶导数并将式(41)代入可得
(74)
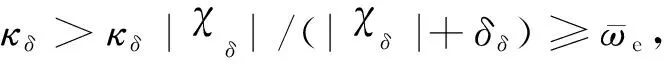
4 仿真验证



图2 情形1仿真结果Fig.2 Simulation results of situation 1
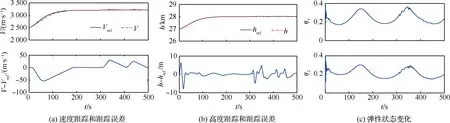

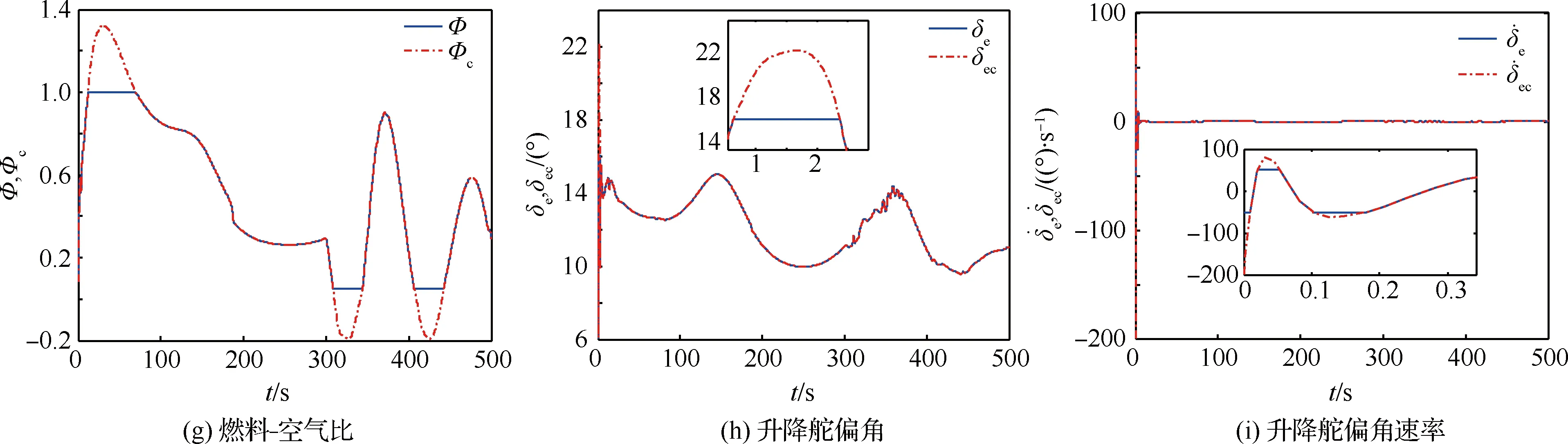
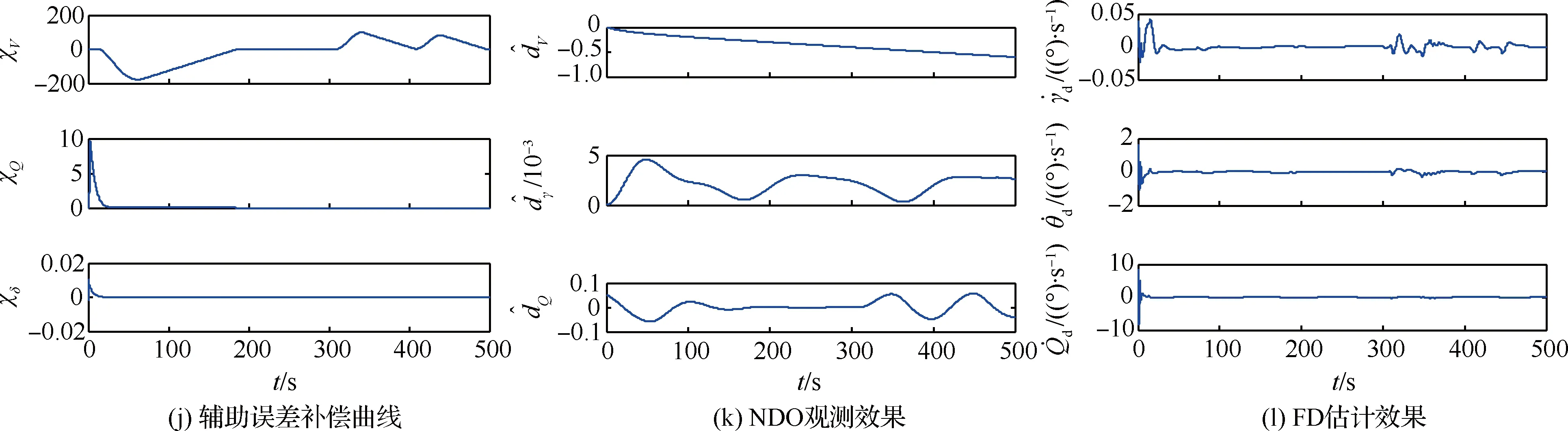
图3 情形2仿真结果Fig.3 Simulation result of Situation 2
5 结 论
1) 本文基于辅助误差补偿策略设计的AHV鲁棒反演控制律,保证了执行机构在幅值和速率达到瞬时饱和时闭环控制系统的稳定性和跟踪误差的有界性。
2) 所设计的FD和NDO,实现了对虚拟控制律及其一阶导数的精确估计,并完成了对模型不确定项的平滑估计,进一步提高了控制精度。
3) 仿真结果充分表明,所提出的控制策略在处理更为严苛的控制输入受限问题时,比现有方法有一定的优越性。
[1] DUAN H B, LI P. Progress in control approaches for hypersonic vehicle[J]. Science China Technological Sciences, 2012, 55(10): 2965-2970.
[2] XU B, SHI Z K. An overview on flight dynamics and control approaches for hypersonic vehicles[J]. Science China Information Sciences, 2015, 58(7): 070201-1-19.
[3] 吴宏鑫, 孟斌. 高超声速飞行器控制研究综述[J]. 力学进展, 2009, 39(6): 756-765.
WU H X, MENG B. Review on the control of hypersonic flight vehicles[J]. Advances in Mechanics, 2009, 39(6): 756-765 (in Chinese).
[4] 方洋旺, 柴栋. 吸气式高超声速飞行器制导与控制研究现状及发展趋势[J]. 航空学报, 2014, 35(7): 1776-1786.
FANG Y W, CHAI D. Status and development trend of the guidance and control for air-breathing hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinca, 2014, 35(7): 1776-1786 (in Chinese).
[5] 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913.
SUN C Y, MU C X, YU Y. Some control problems for near space hypersonic vehicles[J]. Acta Automatica Sinica, 2013, 39(11): 1901-1913 (in Chinese).
[6] 葛东明. 临近空间高超声速飞行器鲁棒变增益控制[D]. 哈尔滨: 哈尔滨工业大学, 2011.
GE D M, Robust gain-scheduling control of hypersonic vehicle in near space[D]. Harbin: Harbin Institute of Technology, 2011 (in Chinese).
[7] XU B, SHI Z K, YANG C G, et al. Neural control of hypersonic flight vehicle model via time-scale decomposition with throttle setting constraint[J]. Nonlinear Dynamics, 2013, 73: 1849-1861.
[8] GAO G, WANG J Z. Reference command tracking control for an air-breathing hypersonic vehicle with parametric uncertainties[J]. Journal of the Franklin Institute, 2013, 350: 1155- 1188.
[9] GAO G, WANG J Z, WANG X H. Robust tracking control for an air-breathing hypersonic vehicle with input constraints[J]. International Journal of Systems Science, 2014, 45(12): 2466-2479.
[10] XU B, HUANG X Y, WANG D W, et al. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation[J]. Asian Journal of Control, 2014, 16(1): 162-174.
[11] XU B, WANG S X, GAO D X, et al. Command filter based robust nonlinear control of hypersonic aircraft with magnitude constraints on states and actuators[J]. Journal of Intelligent & Robotic Systems, 2014, 73: 233-247.
[12] 李静, 左斌. 输入受限的吸气式高超声速飞行器自适应Terminal滑模控制[J]. 航空学报, 2012, 33(2): 220-233.
LI J, ZUO B. Adaptive terminal sliding mode control for air-breathing hypersonic vehicles under control input constraints[J]. Acta Aeronautica et Astronautica Sinca, 2012, 33(2): 220-233 (in Chinese).
[13] ZONG Q, WANG F, TIAN B L, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J]. Nonlinear Dynamics, 2014, 78: 289-315.
[14] CHEN M, GE S S, REN B B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints[J]. Automatica, 2011, 47(3): 452-465.
[15] BU X W, WU X Y, MA Z, et al. Novel auxiliary error compensation design for the adaptive neural control of a constrained flexible air-breathing hypersonic vehicle[J]. Neurocomputing, 2016, 171: 313-324.
[16] FARRELL J, SHARMA M, POLYCARPOU M. Backstepping-based flight control with adaptive function approximation[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(6): 1089-1102.
[17] BU X W, WU X Y, TIAN M Y, et al. High-order tracking differentiator based adaptive neural control of a flexible air-breathing hypersonic vehicle subject to actuators constraints[J]. ISA Transactions, 2015, 58: 237-247.
[18] PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869.
[19] BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374-387.
[20] FIORENTINI L, SERRANI A. Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model[J]. Automatica, 2012, 48: 1248-1261.
[21] FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-416.
[22] 时建明, 王洁, 王琨, 等. 吸气式高超声速飞行器纵向运动反演控制器设计[J]. 西安交通大学学报, 2013, 47(3): 102-107.
SHI J M, WANG J, WANG K, et al. Design of backstepping controller for longitudinal motion of an air-breathing hypersonic vehicle[J]. Journal of Xi’an Jiaotong University, 2013, 47(3): 102-107 (in Chinese).
[23] 王肖, 郭杰. 吸气式高超声速飞行器鲁棒非奇异Terminal滑模反步控制[J]. 航空学报, 2017, 38(3): 320287.
WANG X, GUO J. Robust nonsingular Terminal sliding mode backstepping control foe air-breathing hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinca, 2017, 38(3): 320287 (in Chinese).
[24] XU B, GAO D X, WANG S X. Adaptive neural control based on HGO for hypersonic flight vehicles[J]. Science China Information Sciences, 2011, 54(3): 511-520.
[25] BU X W, WU X Y, CHEN Y X, et al. Design of a class of new nonlinear disturbance observers based on tracking differentiators for uncertain dynamic systems[J]. International Journal of Control, Automation, and Systems, 2015, 13(3): 595-602.
[26] WANG X H, CHEN Z Q, YANG G. Finite-time-convergent differentiator based on singular perturbation technique[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1731-1737.

