基于数值模拟的NSDBD等离子体激励器防冰特性

贾韫泽，桑为民，蔡旸

西北工业大学 航空学院，西安 710072

飞行器在积冰气象条件下飞行时，由于过冷水滴的撞击在其表面形成的积冰会使气动性能下降。在积冰条件下，防冰系统保障在飞行安全方面尤为重要。

对于飞机积冰的研究，通常包括：积冰预测、防/除冰措施研究、积冰对空气流场影响等。在积冰预测研究中水滴的收集情况是重要的一部分，Durst等[1]使用拉格朗日方法和欧拉方法求解水滴碰撞情况，计算发现两种方法得到的结果基本一致。基于控制体内的质量与能量平衡，Messinger[2]建立了积冰质量、能量平衡方程。基于Messinger模型,Macarthur[3]考虑了溢流水的影响，对霜冰与光冰条件下的冰型进行了预测，与试验对比良好。随着研究的增多，出现了许多商用的积冰预测软件，如：LEWICE、ONERA 2D/3D、FENSAP-ICE等。在防冰措施方面，热防冰方法已经得到运用。通过热源的不同，现有热防冰主要分为气热防冰与电热防冰。气热防冰主要是通过引入喷气式发动机的热空气到防冰区，对防冰区进行加热。电防冰是直接通过布置好的发热元件进行加热。电热防冰已在波音787客机的机翼上得到了使用。在数值模拟方面，Al-Khalil[4]、Morency[5]、Silva[6-7]等对气热与电热防冰进行了大量研究。随着近年来对等离子体流动控制的研究不断增多[8]，阻挡介质放电(DBD)等离子体激励器对流场温度的影响已经被注意到[9-11]。这意味着等离子体也可以作为一种热源加入流场中。目前等离子流动控制方面的研究有：流动分离控制[12-13]、激波控制[14-15]、预混空气丙烷点火[16]、升阻控制[17]等。对等离子体激励器进行数值研究的常用方法有：① 粒子单元直接蒙特卡罗方法[18]；② 基于集总电路的方法[19]； ③ 流场方程与泊松电场方程耦合的方法[20-21]； ④ 基于试验与理论结果的唯象学方法[22-24]。唯象学模型不关注放电细节, 仅抓住激励对流场的直接效应, 将激励以动量和能量源项形式耦合到流体方程,节约计算耗时[23]。从目前公开文献来看，等离子体防冰方面研究开展较少，文献[25]中研究人员在圆柱表面布置阻挡介质等离子体激励器，在结冰条件下通过试验研究了等离子体在防/除冰方面的影响。

在本文中，首先建立基于Messinger方法的积冰模型，对于典型光冰霜冰进行验证计算；其次，使用唯象学等离子体模型，计算了纳秒脉冲阻挡介质放电(NSDBD)作用下的空气流场，并对NSDBD等离子体激励器的防冰特性进行了数值研究。

1 数值模拟方法及计算模型

1.1 空气流场计算

采用非定常雷诺平均Navier-Stokes(URANS)方程[24]对流场进行求解，NSDBD等离子体激励器对空气流场的影响作为动量和能量源项与URANS方程耦合，忽略流场对等离子体的影响。

(1)

(2)

(3)

式中:ρ为空气密度；t为时间;ui为速度；xi为空间坐标；μ为空气黏度；cp为空气比热；p为压力；T为温度；τij为切应力张量；h和H分别为焓和总焓；E为总能；Pr为普朗特数；SM为动量源项，不考虑，即SM=0；SE=ERv(x,y)/τR为能量源项，其中τR为热源作用时间，ERv(x,y)为等离子体能量密度，mJ/cm3，将由唯象学等离子体模型给出；符号“-”“″”“～”分别表示参数的雷诺平均值、波动分量和Favre平均值。空气流场求解采用二阶迎风格式、SST(Shear Stress Transport)k-ω湍流模型进行计算。

1.2 水滴轨迹与水滴收集系数

水滴轨迹的求解采用拉格朗日方法，轨迹方程为

(4)

图1为碰撞到翼型表面的水滴轨迹示意图，图中dy′为水滴释放位置的间距，ds为翼型上水滴碰撞位置的间距。Su、Sl分别为上下水滴碰撞极限位置，y′为碰撞极限位置对应的水滴释放位置的间距。在求得水滴轨迹的情况下,局部水滴收集系数β定义为

(5)

图1 水滴轨迹示意图Fig.1 Sketch of droplet trajectories

1.3 积冰热力学模型

本文的积冰热力学模型基于Messinger模型[3,26]考虑一个控制体内的质量与能量守恒，图2为控制体内能量与质量守恒示意图[27]。质量与能量守恒方程分别为

(6)

(7)

在控制体内定义冻结系数F为

(8)

当F=1时表示当前控制体内水全部冻结为冰；当F=0时表示没有任何冻结发生。

流出控制体的水量可表示为

(9)

(10)

式中：A为换热面积；hc为对流换热系数；Ts为表面平衡温度；Tairsurf为与控制体对流换热的空气温度。

图2 控制体内质量与能量守恒示意图[27]Fig.2 Sketch of mass and energy balance of control volume[27]

1.4 唯象学等离子体模型

(11)

文献[28]中的试验也表明能量输入Eenergy(f,U)与激励频率f(Hz)有关:

(12)

同时能量输入Eenergy(f,U,p0)也与大气压p0(单位为torr，1 torr≈133.3 Pa)相关,其表达式为

Eenergy(f,U,p0)=

(13)

式(12)～式(13)中：a、b、c、m、n为唯象学模型的常量，取值见表1。

最后根据能量的空间分布，能量密度分布ERv(x,y)可表示为

(14)

式中:Emission(x,y)与Emissiontotal为能量分布函数,详见文献[23];η为用于加热气体的能量占总能量的百分比。

表1 唯象学模型常量Table 1 Constants of phenomenological model

2 经典算例测试及结果分析

2.1 积冰预测

选取NACA0012翼型，其弦长为0.533 4 m，积冰时间t为360 s，图3、图4给出了霜冰预测结果，计算条件见表2，图5、图6给出了光冰预测结果，计算条件见表3。表2和表3中，AOA为迎角，MVD为平均水滴直径，LWC为液态水含量。

霜冰的计算中选取每60 s更新一次网格进行流场的重新计算。图3显示了每一积冰时间步冰型的增长情况(图中c为弦长,X′为翼型的弦线方向，Y′为与弦线垂直的方向，翼型前缘点为坐标原点，图例clean代表未结冰的干净翼型)。图4中将本文计算结果与文献计算[29]和试验[30]结果进行了对比，发现基于Messinger方法建立的结冰模型能良好地预测霜冰冰型。

图3 各时间步霜冰冰型Fig.3 Shape of rime ice (per time step)

图4 霜冰冰型计算与试验结果的对比Fig.4 Comparison of shapes of rime ice between calculated and experimental results

表2 霜冰计算条件Table 2 Calculation condition of rime ice

ParameterValueAOA/(°)4Velocity/(m·s-1)67.05Temperature/K253.69MVD/μm20LWC/(g·m-3)1.0

光冰的计算中选取每60 s更新一次网格进行流场的重新计算。图5显示了每一积冰时间步冰型的增长情况。图6中将计算结果与试验对比发现，预测的光冰冰型与试验[30]大体趋势一致，有光冰典型的冰角，光冰前缘冰型厚度在X′方向上基本与试验一致。但与试验结果在上冰角有所差距，对比其他计算结果[29-30]发现，与试验均有一定区别。综合霜冰与光冰的计算结果，可以认为本文积冰模型是有效的。

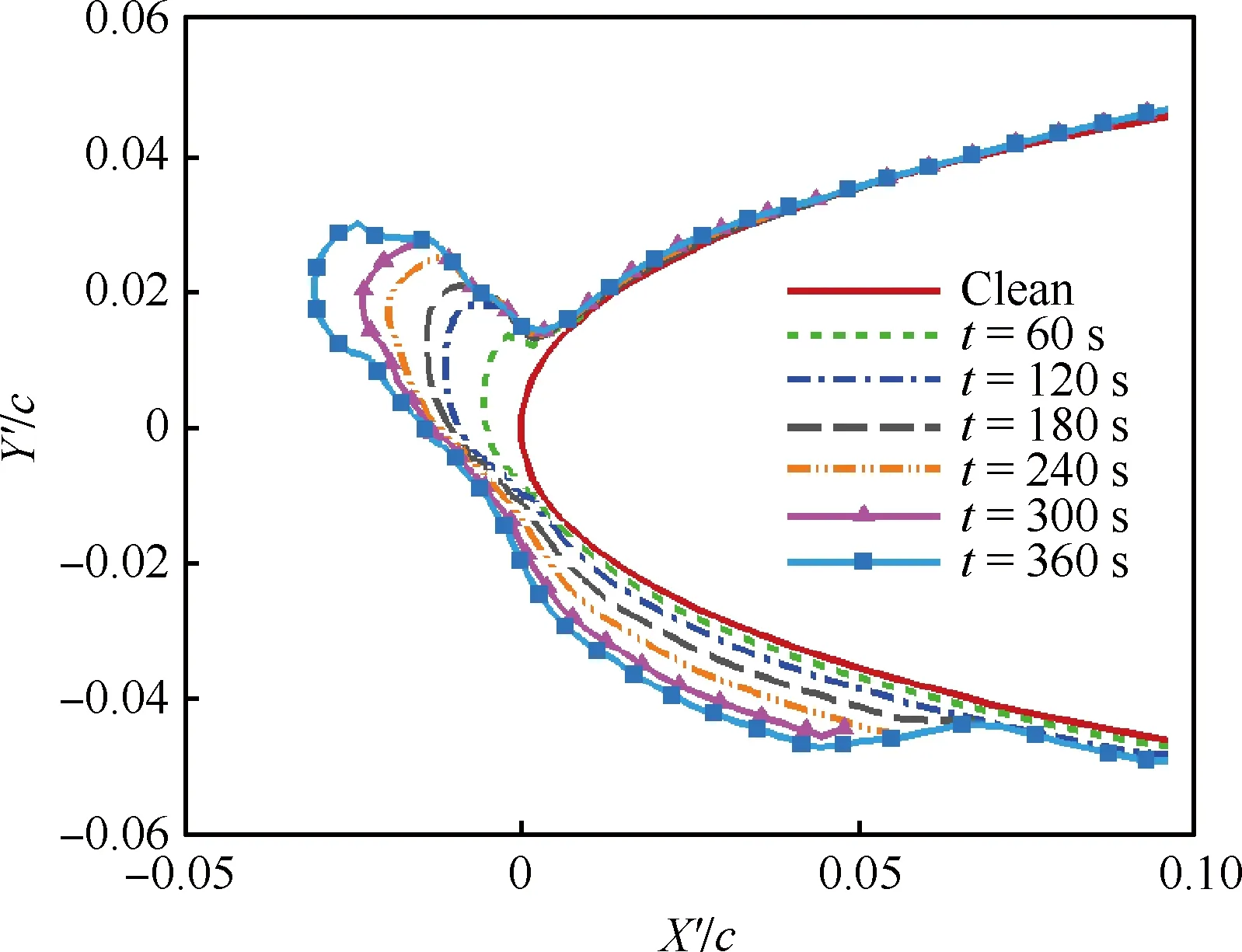
图5 各时间步光冰冰型Fig.5 Shape of glaze ice (per time step)

图6 光冰冰型计算与试验结果的对比Fig.6 Comparison of shapes of glaze ice between calculated and experimental results

表3 光冰计算条件Table 3 Calculation condition of glaze ice

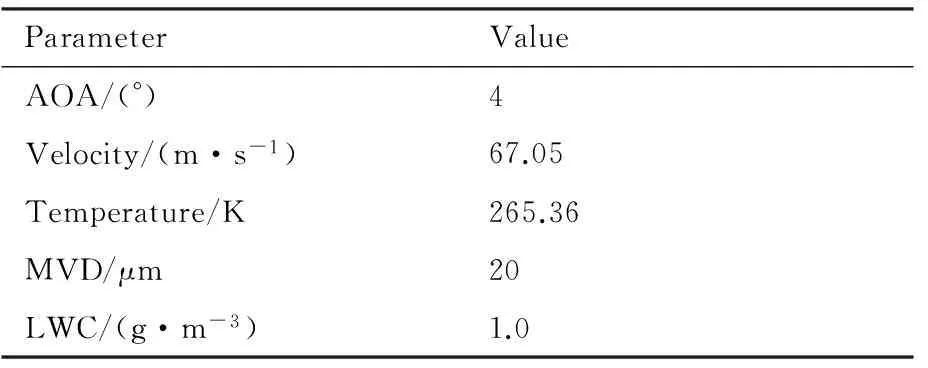
ParameterValueAOA/(°)4Velocity/(m·s-1)67.05Temperature/K265.36MVD/μm20LWC/(g·m-3)1.0

2.2 唯象学等离子模型测试

这部分将应用唯象学等离子体模型与流场耦合求解进行计算，验证算例都为单个等离子体激励器加载在平板上，计算等离子体激励后流场的变化。NSDBD等离子体激励器结构示意图如图7所示,激励器由阴阳电极、阻挡介质组成，等离子体在阴阳电极之间产生。

图7 NSDBD等离子体激励器结构Fig.7 Structure of NSDBD plasma actuator

2.2.1 算例1

本算例中计算条件与文献[21]中的计算条件相同,峰值电压为14 kV，气压为一个标准大气压，空气温度为300 K。选取从激励器开始工作时,与文献[21]相同时间点t=4,8,16,25 μs的压力云图进行对比分析。

图8 等离子体激励器作用下不同时刻的压力云图Fig.8 Contours of pressure at different time with plasma actuator

图8给出了等离子体激励器作用下不同时刻的压力云图。图中Δp是相对大气压的压力值，从图中可以发现在等离子体能量的注入下，流场中形成了圆弧形状的冲击波。其中低压区的发展紧随着高压区。对比图9文献[21]的计算结果，发现本文计算所得波的强度和位置与之基本一致。

图9 文献[21]中不同时刻的压力云图Fig.9 Contours of pressure at different time in Ref. [21]

2.2.2 算例2

为了进一步验证唯象学等离子体激励器模型，同样布置等离子体激励器在平板上，并参照文献[31]中的纹影试验。计算条件与试验相同,峰值电压为50 kV，气压为一个标准大气压，空气温度为300 K。图10为t=16 μs时刻流场的情况，左侧为纹影试验[31],右侧为计算得到的无量纲密度(ρ/ρ0)云图。

图10 纹影试验[31]与计算结果对比(t=16 μs) Fig.10 Comparison of shadow image between experimental[31] and calculated results (t=16 μs)

图11 波的位置计算与试验[31]结果对比Fig.11 Comparison of wave positions between calculated and experimental[31] results

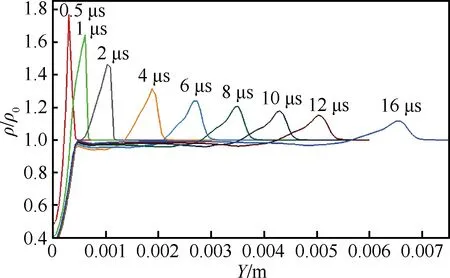
图12 不同时刻在X=-0.001 5 m处沿Y方向的 无量纲密度分布 Fig.12 Distribution of dimensionless density for different time at X=-0.001 5 m in Y direction

从图10中可以发现在t=16 μs时刻，计算的圆弧形冲击波的形状与纹影试验结果[31]基本一致。图11取X=-0.001 5 m处波在Y方向的位置，与试验结果[31]相对比。发现波的传播速度与试验相一致，这意味着波的强度得到了比较好的预测。图12给出了0.5 μs≤t≤16 μs时间范围内X=-0.001 5 m处波在Y方向上无量纲密度的分布。观察图像可以发现有1道压缩波从壁面处生成，其后跟着1道比较弱的膨胀波。在0.5 μs≤t≤2 μs时间范围内压缩波的宽度较窄，且强度较大。随着波的传播，膨胀波逐渐赶上压缩波，压缩波强度逐渐降低。

综上两个等离子体的算例，可以说明唯象学模型能较好地反应出等离子体能量的注入对流场的影响。

3 NSDBD等离子体激励器防冰特性

在积冰模型和唯象学等离子体模型的基础上，本节将结合这两种模型，对NSDBD等离子体激励器防冰特性进行分析。

3.1 NSDBD等离子体激励器分布

首先将等离子激励器安置在NACA0012翼型前缘，内置电极、外漏电极按照流向分布，布置位置见图13。根据唯象学模型仅抓住激励对流场的直接效应, 将激励以能量源项形式耦合到流体方程，按前述式(14)进行计算。由唯象学模型考虑将等离子体对空气流场的影响耦合进能量源项，得到的无量纲能量密度分布见图14，记为状态A。根据图14可以看能量密度主要分布在等离子体激励器外漏电极与内埋电极之间，这与等离子体激励器放电过程中产生等离子体的位置一致。根据文献[30]中的试验研究，其环境温度在244.75～268.7 K之间。为验证等离子体防冰的有效性，选择较为极端的低温环境(244.75 K)进行数值模拟，其他计算条件详见表4。

图13 NACA0012翼型上NSDBD等离子体激励器的 分布(状态A)Fig.13 Distribution of NSDBD plasma actuator on NACA0012 airfoil (State A)

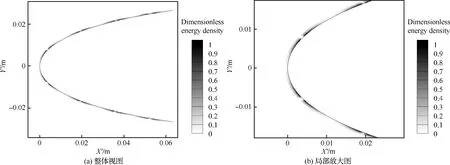
图14 NACA0012翼型上无量纲能量密度分布Fig.14 Distribution of dimensionless energy density on NACA0012 airfoil

表4 防冰计算条件Table 4 Calculation condition of anti-icing

ParameterValueAOA/(°)4Velocity/(m·s-1)67.05Temperature/K244.75MVD/μm20LWC/(g·m-3)1.0

在本节防冰数值计算时等离子体激励器参数为：峰值电压30 kV, 激励器频率4 kHz, 环境压力101 300 Pa。文献[25]对阻挡介质等离子体激励器防冰进行了试验研究，试验环境温度为263.75 K，选取的激励器电压为15 kV。在本文中计算环境温度为244.75 K，因此依照此环境温度，最后选择更高的峰值电压30 kV。

3.2 NSDBD等离子体开启时的流场结果

为了分析NSDBD等离子体激励器对流场的影响，首先计算了不加载等离子体时的流场，压力云图和温度云图见图15(a)与图16(a)。采用URANS方法对等离子体作用下的流场进行计算。选取的激励频率为4 kHz，周期则为250 μs。图15与图16给出了不同时刻的压力与温度云图。图15中Δp是相对于环境压力(101 300 Pa)的压力值。

图15 不同时刻的压力云图与流线分布Fig.15 Contours of pressure and distribution of streamlines at different time

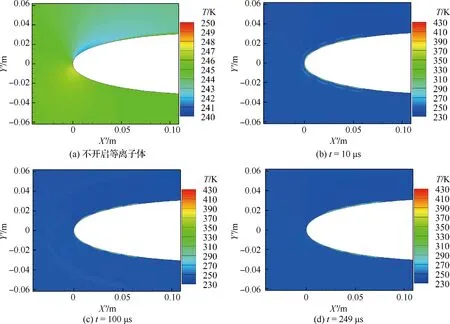
图16 不同时刻的温度云图Fig.16 Contours of temperature at different time

根据图15和图16，可以发现等离子对翼型周围流场的影响主要分为两方面：① 形成冲击波；② 加热翼型表面空气。对比图15(a)～图15(d)可以发现。等离子体引起翼型表面的压力变化形成冲击波，改变了周围流动，流线有种被“冲散”的现象。随着时间推移，图15(c)～图15(d)所对应的时间段内，可以发现这种冲击效应逐渐减弱，变得不明显，由翼型表面向远场扩散。对比图16(a)～图16(d)的温度云图可以发现，在NSDBD等离子体激励器作用下机翼表面被高温气体所覆盖。在一个激励周期内(250 μs)翼型表面的气体一直保持在一个较高的温度。图17给出了翼型表面气体在一个激励周期内时间平均温度(Tmean)与不加等离子体时的对比。图17中横轴为翼型表面距离驻点的位置(S)除以弦长得到的无量纲长度。在NSDBD等离子体激励器开启时，翼型前缘表面的时间平均空气温度要远高于不开启时，且气流温度在273.15 K之上。图18给出了驻点处空气温度在一个激励周期内的变化，驻点处的空气被快速加热到一个较高的温度，在等离子体放电结束之后空气与周围发生对流后温度逐渐降低。可见这些在翼型周围保持较长时间的高温气体将会起到防冰作用。

图17 翼型前缘时间平均空气温度对比Fig.17 Comparison of time-averaged air temperature around airfoil at leading edge

图18 驻点附近空气温度在一个激励周期内的变化Fig.18 Variation of air temperature around stagnation point in a pulse period

3.3 NSDBD等离子体激励器防冰结果

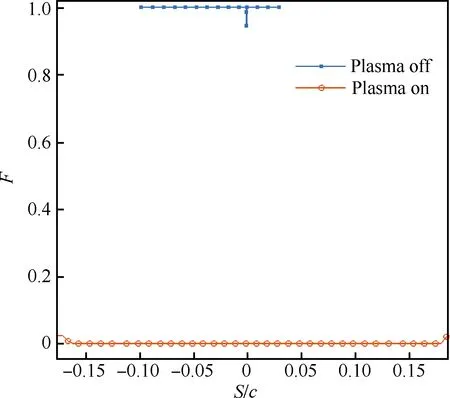
图19 冻结系数对比Fig.19 Comparison of freezing fraction

图20 t=60 s时的冰型对比Fig.20 Comparison of ice shapes at t=60 s

在3.2节计算结果的基础上，考虑到NSDBD等离子体激励器对防冰在温度方面的影响，将激励器一周期的时间平均翼型前缘空气温度耦合进积冰模型的式(10)中进行计算。由于目前尚未考虑积冰表面对等离子体激励器的影响。因此积冰模型中，仅由干净翼型向前推进一个时间步，计算经过Δt=60 s后的情况。图19与图20分别给出了表4积冰条件下的冻结系数与推进一个时间步的冰型。图19中可以看出，当不开启等离子体激励器时，冻结系数F基本上为1，这意味着水滴碰撞到机翼表面立即发生冻结。开启等离子体激励器时，冻结系数基本为0，这表示没有发生冻结形成积冰。图20更直观地显示出在开启等离子体激励器时，前缘防冰区没有积冰出现。可见等离子体影响下在翼型前缘形成的高温气体起到了防冰作用。

3.4 NSDBD等离子体激励器防冰特性

按照前述的方法，对等离子体激励器参数对其防冰特性的影响进一步开展了研究。流场环境条件与3.3节中的相同，具体见表4。

3.4.1 峰值电压对防冰效果的影响

积冰时间为60 s，等离子体激励器的布置与3.1节中相同，激励器频率为4 kHz,选取不同峰值电压(U=15，20，27，30 kV)进行计算，结果见图21。

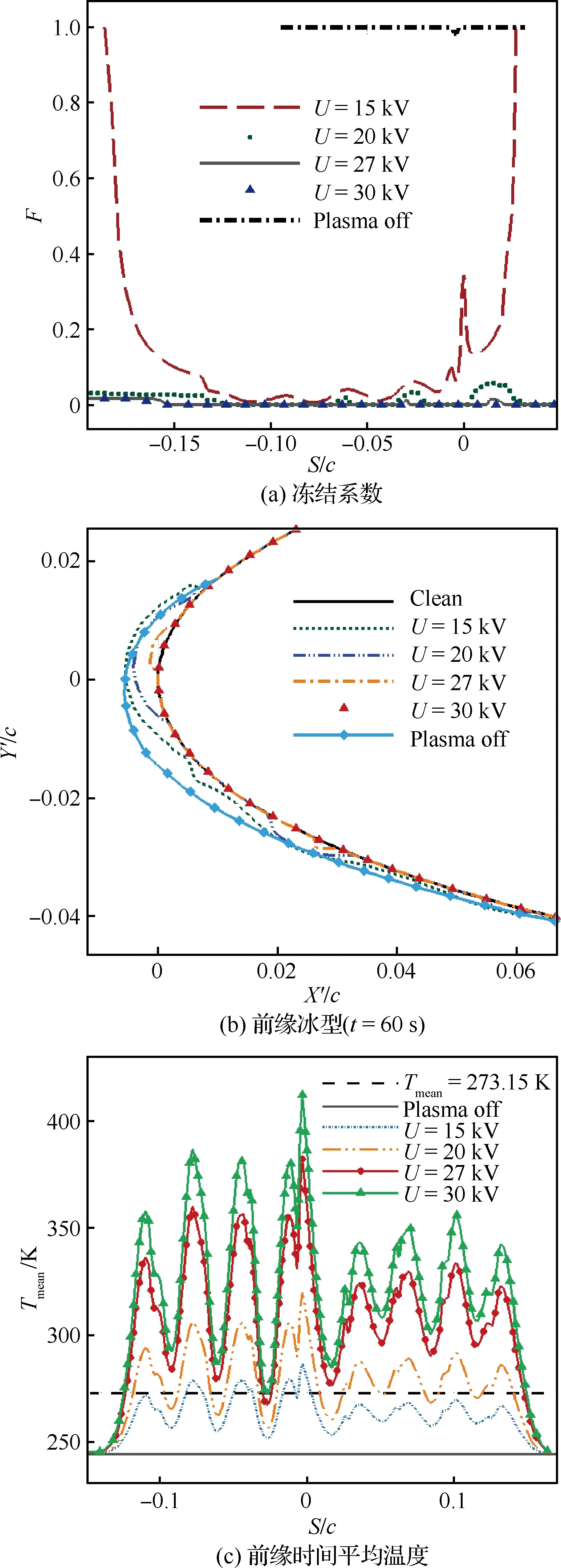
图21 不同峰值电压下的防冰特性Fig.21 Anti-icing property at different peak voltages

图21(b)为不同峰值电压下冰型的对比，在30 kV时，没有积冰产生。在15～27 kV时有积冰出现，且随着峰值电压降低，积冰越严重。由图21(a)可知，在峰值电压为15 kV时，冻结系数有点类似于光冰，即碰撞到翼型表面的水滴没有立即发生冻结，而是有部分向后溢流。15 kV时的冰型有点类似于光冰，有冰角出现。根据图21(c)，可以看到15 kV时的前缘空气平均温度在273.15 K附近，而其他峰值电压下，平均温度基本都高于273.15 K。这种温度的差异导致在15 kV时积冰较严重，其他所计算的峰值电压下，虽还有积冰产生，但并不多。这种峰值电压引起的温度上的差异，通过分析唯象学模型式(11)可以看到，峰值电压越高，等离子体能量输入就越高，导致了高电压产生较高的温度。并且由于等离子体激励器分布位置都与图13中的一致，这几个峰值电压下的温度图像有着相同的趋势。总体上电压的大小对等离子体防冰效果有着较大影响。从能量的角度考虑，存在最优的防冰电压取值。可以看到27 kV时尚未完全防止结冰产生，30 kV时已看不到冰层出现。在27～30 kV之间，选取更多的电压(U=28,29 kV)进行计算，在计算过程中得到的冰型见图22，最后可以看出最优防冰电压区间为29～29.25 kV。

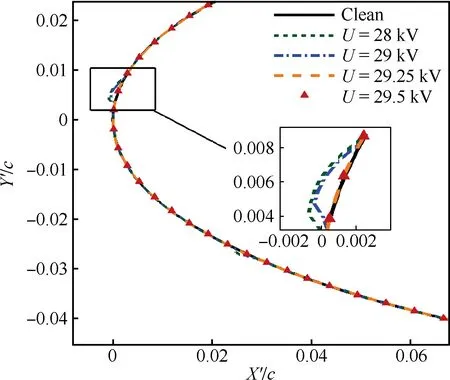
图22 不同峰值电压对应的冰型Fig.22 Ice shapes at different peak voltages

3.4.2 激励器频率对防冰效果的影响

积冰时间为60 s，等离子体激励器的布置能量分布与3.1节相同，峰值电压选取为30 kV,选取不同激励频率(f=1，2，4 kHz)进行计算，结果见图23。

图23 不同激励频率下的防冰特性Fig.23 Anti-icing property at different plus frequencies

图23(b)给出了峰值电压为30 kV时不同激励频率下，等离子体激励器开启时翼型前缘积冰情况。在4 kHz时前缘没有积冰，在1 kHz与2 kHz 时仍有积冰产生。图23(c)中更高的激励频率对应着较高的温度。虽然激励器分布位置相同，但在不同的激励频率下温度曲线上没有显现出相同的趋势。分析唯象学模型式(12)，激励频率越高，等离子体能量越大，使得翼型表面空气温度越高。由于图23(c)中温度为一个激励周期的时间平均温度，激励频率越低，则激励周期越长。也就是说激励频率较低时，翼型表面的高温气体与周围环境中的冷空气有较长的热交换时间。导致激励频率低时温度曲线表现得更加平滑，如图23(c)中f=1 kHz的曲线。在图23(c)中也能发现高温气体随着热交换时间的增加，在翼型表面覆盖的范围更广，有延翼型表面向下游发展的趋势。综上，在较低的激励频率下翼型表面的气温较低，有大范围低于273.15 K的情况，使得低频率下NSDBD等离子体激励器防冰效果较差。根据上述计算，在其他给定条件不变的情况下，从能量的角度，大致可以看出最优激励频率选择范围应在2～4 kHz。

3.4.3 激励器的布置方式对防冰效果的影响

若将NSDBD等离子体激励器外漏电极与内埋电极位置交换，那么其能量密度的分布也将反向。按照图13的等离子体激励器位置，将其电极位置交换，得到新的电极分布如图24所示，得到的反向能量密度分布见图25。记这个新的能量密度分布为状态B。积冰条件见表4，积冰时间为60 s。等离子体激励器参数为：峰值电压30 kV，激励频率4 kHz。计算结果与按图13中的能量分布方式所得结果的对比见图26。

在图26中，State A曲线代表按照图13中的能量密度分布计算所得的结果；State B曲线代表按照图25反向分布的能量密度计算所得结果。观察图26(b)可以发现B状态下有积冰产生，防冰效果没有原状态好。由于峰值电压与激励频率以及环境气压都相同，根据唯象学模型，这两种等离子体激励器布置方式注入的总能量是相同的。观察图25(b)可以发现在驻点附近能量密度处于较低的水平。从图26(c)中状态B的温度分布也可以看到驻点附近的温度处于较低状态(低于273.15 K)，加上驻点附近的热交换较为剧烈，驻点附近发生水滴冻结的现象，从图26(a)中也可以看到驻点附近冻结系数较大。可以发现等离子激励器分布对防冰特性的影响需要具体分析，即使注入总能量相同的条件下，防冰特性也会不同。

图24 NACA0012翼型上NSDBD激励器的分布 (状态B)Fig.24 Distribution of NSDBD plasma actuator on NACA0012 airfoil (State B)

图25 NACA0012翼型无量纲能量密度反向分布Fig.25 Distribution of dimensionless energy density in opposite direction on NACA0012 airfoil

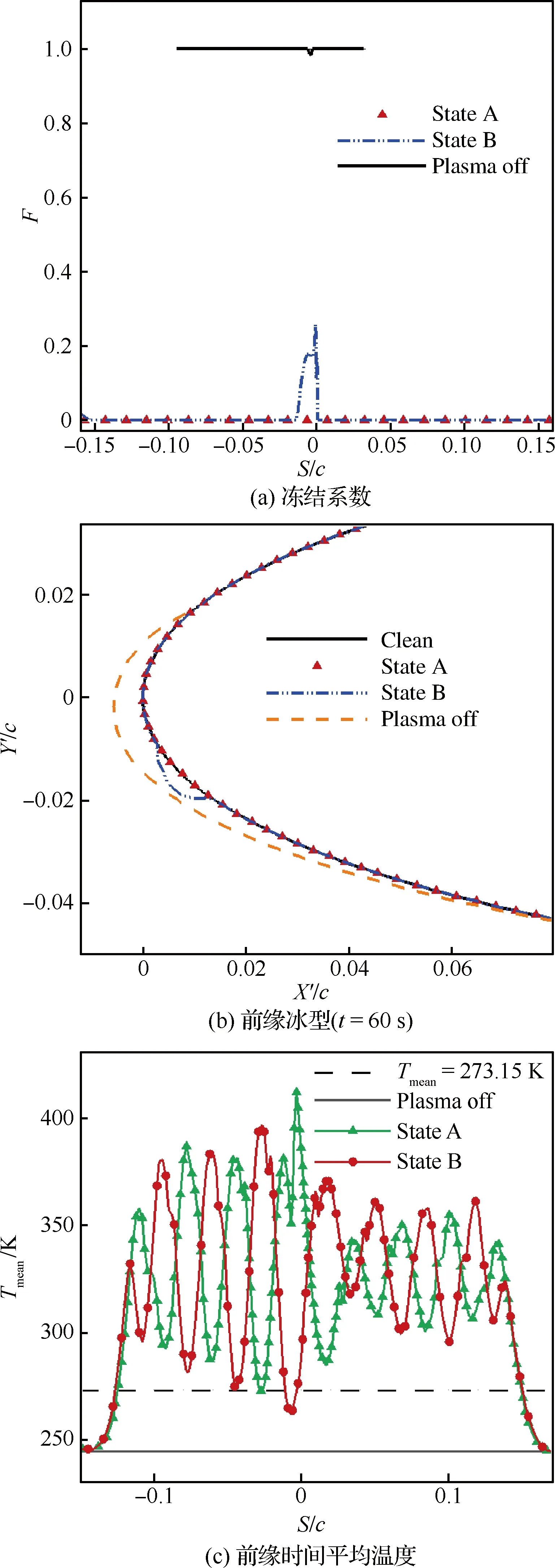
图26 不同能量密度分布下的防冰特性Fig.26 Anti-icing property at different distribution of energy density

3.4.4 NSDBD等离子激励器防冰能耗分析

根据唯象学模型，可以得到等离子体激励器的能量密度分布，进而可以求得等离子体的功率密度。激励频率取4 kHz时不同峰值电压下对应的能量密度与等离子体的功率密度见图27。需要注意的是由于使用唯象学模型进行计算，因此这里提到的等离子体功率密度，仅为等离子体影响范围内等离子体提供的功率，并不是等离子体激励装置总体的能量消耗。

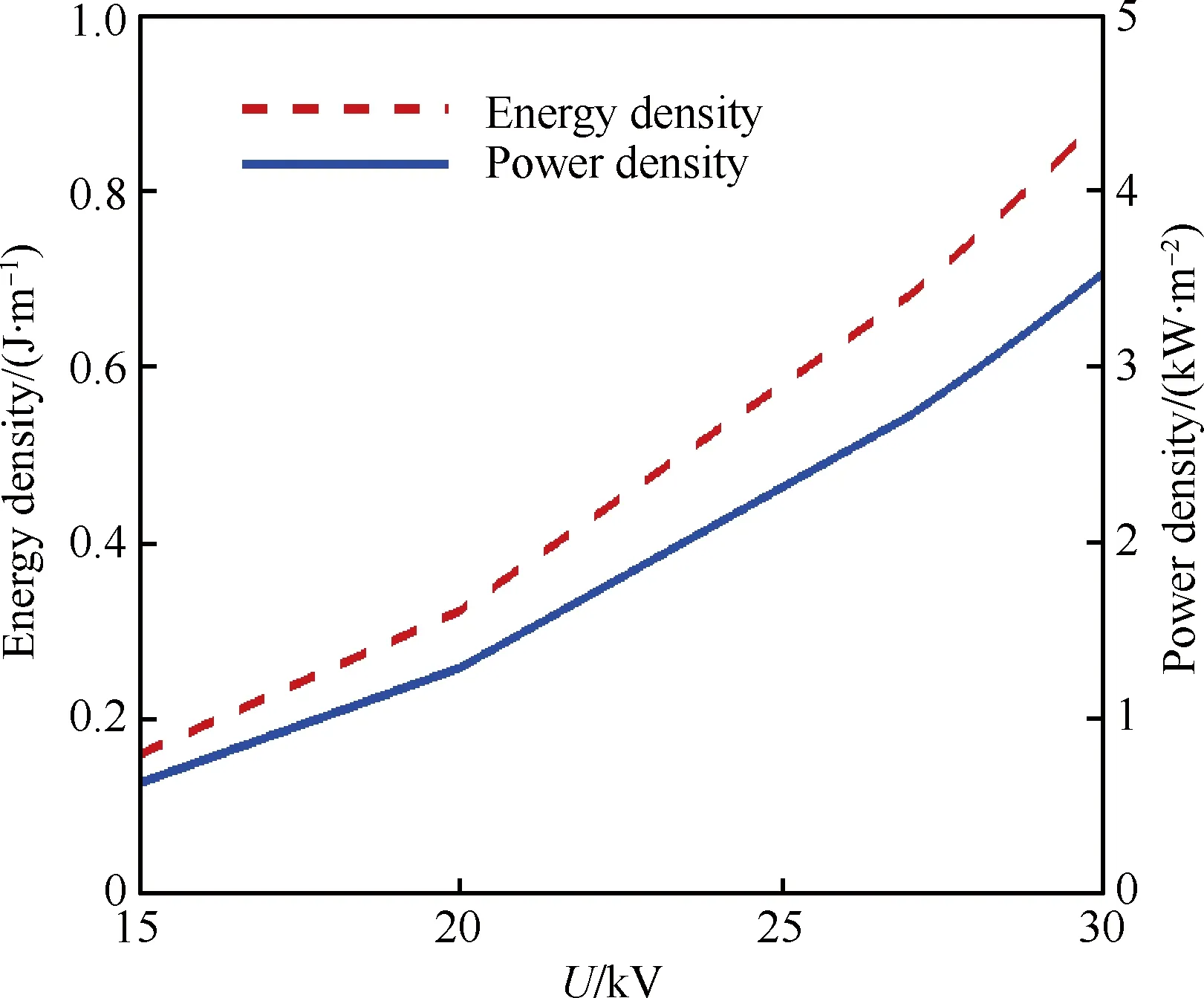
图27 不同峰值电压下的等离子能量密度与功率密度Fig.27 Energy density and power density of plasma at different peak voltages

据3.4.1节的计算分析可知等离子体激励器最优电压取值区间在29～29.25 kV，对应的功率密度大小为3.24～3.31 kW/m2。根据文献[6-7]中的电热防冰计算，其来流速度为89.4 m/s，环境温度为251.55 K，液态水含量为0.55 g/m3，水滴直径为20 μm，防冰电加热能量密度选择在18.6～43.3 kW/m2的范围内。虽然文献中的条件与本文等离子体防冰计算时的有差别，但从功率密度的角度可以看到等离子功率密度要小于电加热功率密度，从整体能耗方面考虑，这对降低防冰系统总能耗是有帮助的。未来的工作中将进一步完善计算模型并分析等离子体防冰装置的总能耗，将其与电热装置总能耗的差异进行研究。

4 结 论

1) NSDBD等离子体激励器对空气流场的影响通过唯象学模型计算，发现其能快速加热周围气体，使翼面附近温度升高，峰值电压对其影响较大。在本文环境条件下存在的最优防冰效果峰值电压的取值区间为29～29.25 kV。

2) NSDBD等离子体激励器激励频率对防冰效果的影响有两方面：① 激励频率越大，等离子体注入能量越大，翼面气流温度越高，防冰效果越好；② 激励频率较低时，激励周期较长，一个周期内，翼面高温气体与环境冷空气热交换时间较长，此时气流温度进一步降低，防冰效果不佳。

3) NSDBD等离子体激励器布置方式对防冰效果的影响需要具体分析。即使等离子体输入的总能量相同，在不同的布置方式下也可能会有不同的防冰效果。

4) 根据唯象学模型计算出等离子体的功率密度，将其与典型电热防冰功率密度比较，等离子体功率密度较低，对降低防冰装置整体能耗方面是有利的。

[1] DURST F, MILOIEVIC D, SCHÖNUNG B. Eulerian and lagrangian predictions of particulate two-phase flows: A numerical study[J]. Applied Mathematical Modelling, 1984, 8(2): 101-115.

[2] MESSINGER B L. Equilibrium temperature of an unheated icing surface as a function of airspeed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29-42.

[3] MACARTHUR C D. Numerical simulation of airfoil ice accretion: AIAA-1983-0112[R]. Reston, VA: AIAA, 1983.

[4] AL-KHALIL K M, HORVATH C, MILLER D R, et al. Validation of NASA thermal ice protection computer codes. Ⅲ—The validation of ANTICE: AIAA-1997-0051[R]. Reston, VA: AIAA, 1997.

[5] MORENCY F, BRAHIMI M T, TEZOK F, et al. Hot air anti-icing system modelization in the ice predict ion code CANICE: AIAA-1998-0192[R]. Reston, VA: AIAA, 1998.

[6] SILVA G A L, SILVARES O M, ZERBINI E J G J. Numerical simulation of airfoil thermal anti-ice operation: Part Ⅰ—Mathematical modeling[J]. Journal of Aircraft, 2007, 44(2): 627-634.

[7] SILVA G A L, SILVARES O M, ZERBINI E J G J. Numerical simulation of airfoil thermal anti-ice operation: Part Ⅱ—Implementation and results[J]. Journal of Aircraft, 2007, 44(2): 635-641.

[8] ROTH J R, SHERMAN D M, WILKINSON S P.Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma: AIAA-1998-0328[R]. Reston, VA: AIAA, 1998.

[9] WINKEL R, CORREALE G, KOTSONIS M. Effect of dielectric material on thermal effect produced by ns-DBD plasma actuator: AIAA-2014-2119[R]. Reston, VA: AIAA, 2014.

[10] ERFANI R, HALE C, KONTIS K. The influence of electrode configuration and dielectric temperature on plasma actuator performance: AIAA-2011-0955[R]. Reston, VA: AIAA, 2011.

[11] NUDNOVA M, KINDUSHEVA S, ALEKSAHDROV N, et al. Rate of plasma thermalization of pulsed nanosecond surface dielectric barrier discharge: AIAA-2010-0465[R]. Reston, VA: AIAA, 2010.

[12] ROUPASSOV D V, NIKIPELOV A A, NUDNOVA M M, et al. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge[J]. AIAA Journal, 2009, 47(1):168-185.

[13] LITTLE J, TAKASHIMA K, NISHIHARA M, et al. Separation control with nanosecond-pulse-driven dielectric barrier discharge plasma actuators[J]. AIAA Journal, 2012, 50(2): 350-365.

[14] SHANG J S, MENART J, KIMMEL R, et al. Hypersonic inlet with plasma induced compression: AIAA-2006-0764[R]. Reston, VA: AIAA, 2006.

[15] NISHIHARA M, TAKASHIMA K, RICH J W, et al. Mach 5 bow shock control by a nanosecond pulse surface DBD: AIAA-2011-1144[R]. Reston, VA: AIAA, 2011.

[16] GALLEY D, PILLA G, LACOSTE D, et al. Plasma-enhanced combustion of a lean premixed air-propane turbulent flame using a nanosecond repetitively pulsed plasma: AIAA-2005-1193[R]. Reston, VA: AIAA, 2005.

[17] MIZOKAMI T, NOGUCHI D, FUKAGATA K. Lift and drag control using dielectric barrier discharge plasma actuators installed on the wingtips: AIAA-2013-2456[R]. Reston, VA: AIAA, 2013.

[18] FONT G I, JUNG S, ENLOE C L, et al. Simulation of the effects of force and heat produced by a plasma actuator on neutral flow evolution: AIAA-2006-0167[R]. Reston, VA: AIAA, 2006.

[19] ORLOV D M , CORKE T C, PATEL M P. Electric circuit model for aerodynamic plasma actuator: AIAA-2006-1206[R]. Reston, VA: AIAA, 2006.

[20] BOUEF J P, LAGMICH Y, CALLEGARI T, et al. Electro hydro dynamic force and acceleration in surfaces discharges: AIAA-2006-3574[R]. Reston, VA: AIAA, 2006.

[21] UNFER T, BOEUF J P. Modelling of a nanosecond surface discharge actuator[J]. Journal of Physics D: Applied Physics, 2009, 42(19): 194017-194028.

[22] SUZEN Y B, HUANG P G, JACOB J D, et al. Numerical simulations of plasma based flow control applications: AIAA-2005-4633[R]. Reston, VA: AIAA, 2005.

[23] 赵光银， 李应红， 梁华， 等. 纳秒脉冲表面介质阻挡等离子体激励唯象学仿真[J].物理学报, 2015, 64(1): 015101-015111.

ZHAO G Y, LI Y H, LIANG H, et al. Phenomenological modeling of nanosecond pulsed surface dielectric barrier discharge plasma actuation for flow control[J]. Acta Physica Sinica, 2015, 64(1): 015101-015111 (in Chinese).

[24] CHEN Z L, HAO L Z, ZHANG B Q. A model for nanosecond pulsed dielectric barrier discharge actuator and its investigation on the mechanisms of separation control over an airfoil[J]. Science China Technological Sciences, 2013, 56(5): 1055-1065.

[25] CAI J S, TIAN Y Q, MENG X S, et al. An experimental study of icing control using DBD plasma actuator[J]. Experiments in Fluids, 2017, 58(8): 102.

[26] TRAN P, BRAHIMI M T, PARASCHIVOIU I, et al. Ice accretion on aircraft wings with thermodynamics effects: AIAA-1994-0605[R]. Reston, VA: AIAA, 1994.

[27] 易贤, 桂业伟, 朱国林. 飞机三维结冰模型及其数值求解方法[J]. 航空学报, 2010, 31(11): 2152-2158.

YI X, GUI Y W, ZHU G L. Numerical method of a three-dimensional ice accretion model of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2152-2158 (in Chinese).

[28] TAKASHIMA K, ZUZEEK Y, LEMPERT W R, et al. Characterization of surface dielectric barrier discharge plasma sustained by repetitive nanosecond pulses: AIAA-2010-4764[R]. Reston, VA: AIAA, 2010.

[29] FORTIN G, ILINCA A, LAFORTE J, et al. Prediction of 2D airfoil ice accretion by bisection method and by rivulets and beads modeling: AIAA-2003-1076[R]. Reston, VA: AIAA, 2003.

[30] SHIN J, BOND T H. Results of an icing test on a NACA 0012 airfoil in the NASA lewis icing research tunnel: AIAA-1992-0647[R]. Reston, VA: AIAA, 1992.

[31] STARIKOVSKII A Y, ROUPASSOV D V, NIKIPELOV A A, et al. Acoustic noise and flow separation control by plasma actuator: AIAA-2009-0695[R]. Reston, VA: AIAA, 2009.