基于矩阵分解和非凸秩近似的低秩表示算法

山东科技大学 李 帅

低秩表示(Low Rank Repersentation，LRR)是针对高维数据集可近似地认为存在于一个或多个相互独立的低维子空间中，且子空间的类别与观测数据中是否存在未知的异常值的问题，将给定的观测数据进行聚类到各自对应的独立子空间中，同时检测异常值。提出了基于矩阵分解与对数行列式函数的低秩表示模型(Matrix Factorization and Log-determinant Rank Approximation based low-rank representation，MF-LDLRR)，利用矩阵分解技术将大规模矩阵化为三个小矩阵，再以非凸近似函数对数行列式函数替代矩阵核范数来近似矩阵秩函数，解决了核范数秩估计偏差问题，并采用交替方向乘子法求解，最后用谱聚类方法规范化割[1]求的聚类结果。通过实验对比，提出的算法提高计算精确度和效率。

1.低秩表示

在求解(2)式中存在每一次迭代均需进行奇异值分解，求解算法的计算复杂度很高和用核范数秩近似误差的问题。

2.基于矩阵分解和非凸秩近似的低秩表示算法

2.1 MF-LDLRR模型

则MF-LDLRR模型为：

2.2 MF-LDLRR的求解算法

下面用交替方向乘子法求解MF-LDLRR模型，引入辅助变量N，模型(3)转化为：

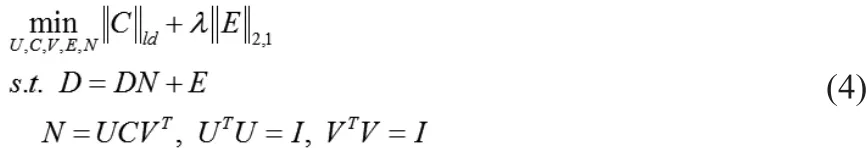
模型(5)的部分增广拉格朗日函数为：

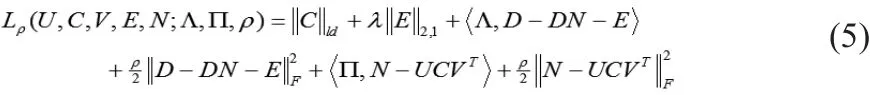
其中Uk+1和Vk+1为Orthogonal Procrustes问题[2]。

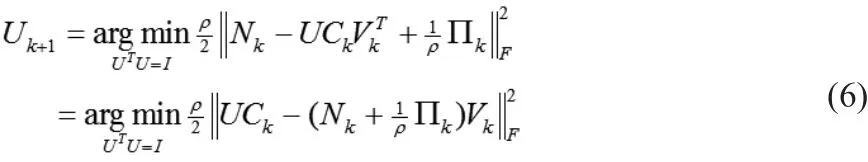
解得：

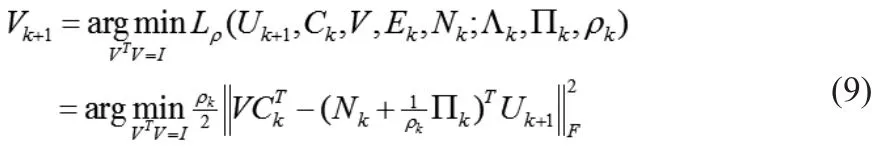
解得：

求解Ck+1：

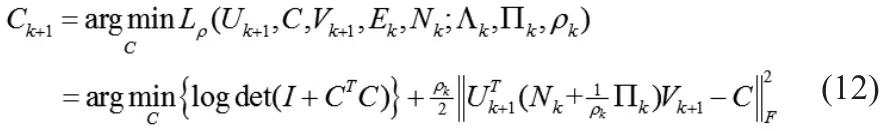
由定理1[3]定理2[3]和性质1[3]求解问题Ck+1的封闭解。

求解Nk+1：

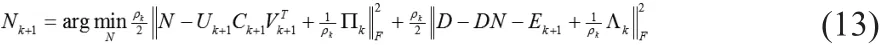
对上(13)式求导得：

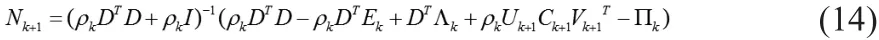
求解Ek+1：

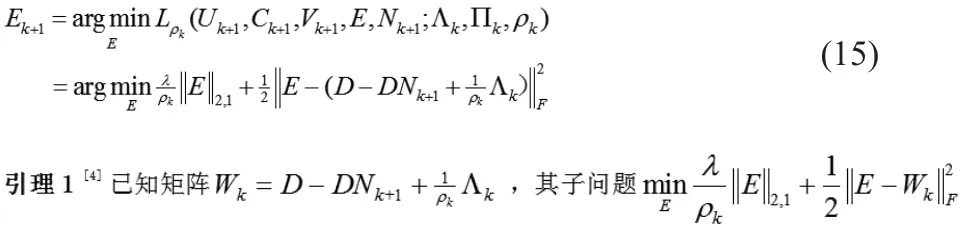
有封闭解Ek+1，Ek+1的第 j 列为：

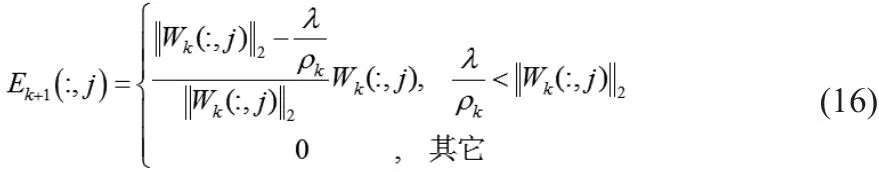
求解拉格朗日乘子，则：

最后更新惩罚参数：

综上所述，具体MF-LDLRR求解算法流程如下所示。

3.实验结果及分析

应用Extended Yale B数据库对MF-LDLLR算法进行验证，与现行LRR,LRSC,SSC等算法相比较。由表1呈现不用算法的分别实验数据结果。

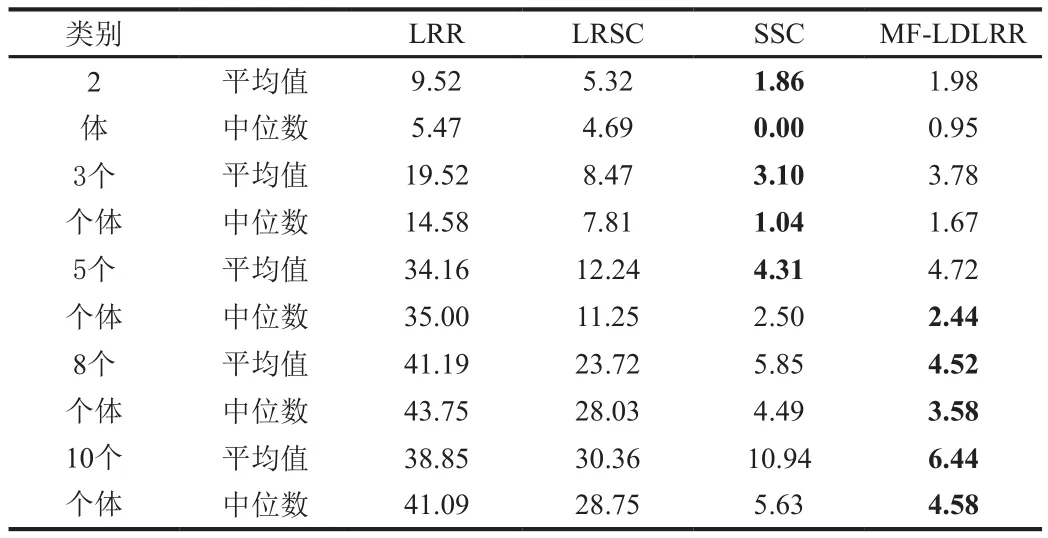
表1 不同算法对Extened Yale B人脸数据集的聚类错误率(%)

从表1知，MF-LDLRR的聚类错误率相对于对象数的增长保持稳定，说明了该算法的鲁棒性。当n ≥5时，提出的算法都比其它算法的聚类错误率低得多。说明了该算法的聚类效果好，且当对象数多的时候，这种优势突出。

4.结论

提出了基于矩阵分解和非凸秩近似的低秩表示模型，该算法复杂度低、精确度高，并在Extended Yale B 数据库上进行实验对比，验证了MF-LDLRR算法有效性。在以后的工作中，模型参数地选择也是研究的重点内容之一。

[1]SHI J, MALIK J．“Normalized cuts and image segmentation”,IEEE Trans[J]．IEEE Transactions on Pattern Analysis & Machine Intellige nce,2000,22(8)∶888-905．

[2]SCHONEMANN P H．A generalized solution of the orthogonal procrustes problem[J]． Psychometrika,1966,31(1)∶1-10．

[3]PENG C,KANG Z,Li H,et al,Subspace Clustering Using Logdeterminant Rank Approximation[C]//Acm Sigkdd International Conference on Knowledge Discovery & Data Mining．Queensland∶ACM,2015∶925-934．

[4]YANY J, YIN W,ZHANG Y, et al． A Fast Algorithm for Edge-Preserving Variational Multichannel Image Restoration[J]．Siam Journal on Imaging Sciences,2009,2(2)∶569-592．