固溶温度对GH4169微观组织形貌及超声特性的影响

，， ，，

(1.南昌航空大学 无损检测教育部重点实验室，南昌 330063；2.中国直升机设计研究所，景德镇 333001；3.北京航空航天大学 机械工程及自动化学院, 北京 100191)

高温合金GH4169是航空发动机机匣部件的主要金属材料，具有耐高温、抗氧化等优点[1]。在制造和服役过程中，GH4169内部组织分布的不均匀会导致环件在加工过程中出现变形，或者机匣在使用过程中出现变形，严重影响航空发动机的安全使用。采用无损检测与金相检测相结合的方法对GH4169构件的微观组织结构进行监测可有效保障制造质量和使用安全。

超声无损检测不仅对宏观缺陷敏感，还可表征组织结构，评价机械性能[2]。超声波在金属中传播时受到晶界、相界、位错等微观结构的影响，声束会发生散射，导致衰减系数、声速、背散射系数等超声信号特征值发生改变。衰减系数对晶粒尺寸变化敏感，两者之间存在较强的正相关性[3-7]，晶粒尺寸越大，衰减系数就越大。声速受到晶粒间结合力和残余应力的影响，对沉淀相含量[8]、析出相[3,9]、相变[10-11]敏感，可用于检测球墨铸铁QT400-18的球化率[12]，在一定程度上能反映钛合金TC4中初生α相的分布[13]。背散射信号同声速、衰减系数一样，可用于珠光体、马氏体、铁素体等组织结构的区别；背散射系数对组织结构性质变化敏感[14-15]，超声背散射功率谱可表征粉末金属合金组织结构中的微孔密度[16]，对背散射信号进行经验模态分解(EMD)后提取固有模态函数(IMF)的平均功率可用于评价晶粒尺寸[17]。超声波在材料中传播时，材料本身会引起非线性声学响应，利用声学非线性特征可表征材料性能和组织结构。与声速、衰减系数相比，非线性系数对组织结构的变化更为敏感，会对析出相、相变的微小变化产生响应[8]，对应力变化敏感，与位错密度之间存在较强的正相关性[18]。

笔者对不同固溶温度下的GH4169合金进行微观组织结构观察和超声检测，分析晶粒形貌变化对超声特性参数的影响，采用经验模态分解的方法对背散射信号进行处理，提取固有模态函数的平均功率和波形维数，探寻GH4169微观形貌无损表征的新参数并验证其有效性。

1 试验过程

在不同固溶温度(900～1 150 ℃)下对GH4169试样进行固溶处理。采用脉冲回波法对试样进行纵波超声检测，探头频率为10 MHz，用一次底波、二次底波的峰值、时间差和试样厚度计算衰减系数、声速，对截取的背散射信号(截取位置为一次底波和二次底波之间，如图1所示)进行经验模态分解，取分解后生成的固有模态函数，计算平均功率ωi和波形维数FSHA，计算公式如式(1)所示。

(1)

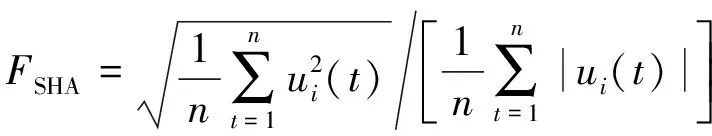
(2)

式中：n为信号长度;i为IMF的阶数;ui(t)为第i阶IMF信号;t为采样点序号。

利用Ritec RAM-5000-SNAP非线性超声测试系统，采用纵波共线谐波法测量并计算非线性系数，发射和接收探头的中心频率分别为2.5，5 MHz。非线性系数计算公式如式(3)所示。

(3)

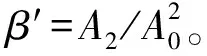
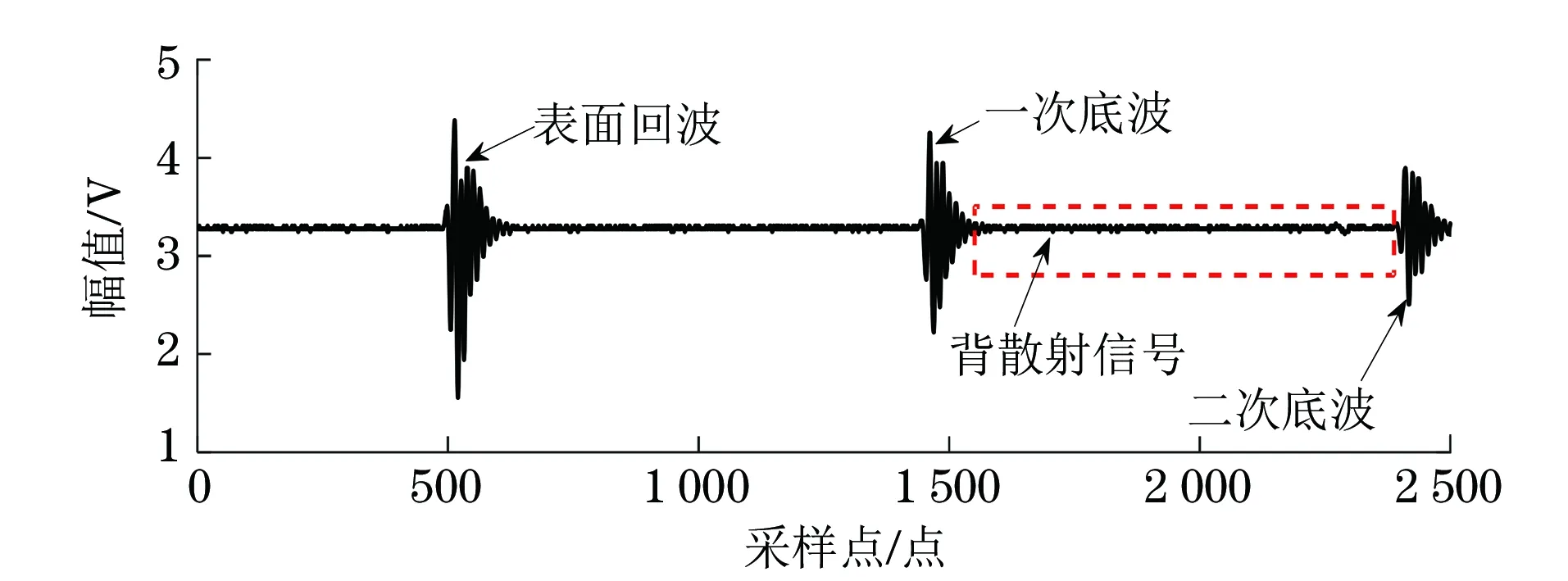
图1 超声A扫信号及背散射信号截取示意

对试样进行金相检验，采用显微镜观察试样微观组织形貌，并运用图像分析软件进行晶粒大小及形状的测量，分别计算平均晶粒直径(晶粒尺寸)和平均晶粒纵横比(晶粒形状)。

2 结果与讨论

2.1 微观组织

GH4169试样的差热分析结果如图2所示，可见在837 ℃时γ′相开始溶解，907 ℃时δ相开始大量析出，982 ℃时δ相开始大量溶解，1 022 ℃时δ相完全溶解，在1 000～1 050 ℃之间GH4169试样发生了固态与固态之间的相的转变。图3为部分试样金相图，从图中可以看出，固溶温度高于相变点后，晶粒尺寸增加迅速，平直型晶界增加，孪晶数量增多。

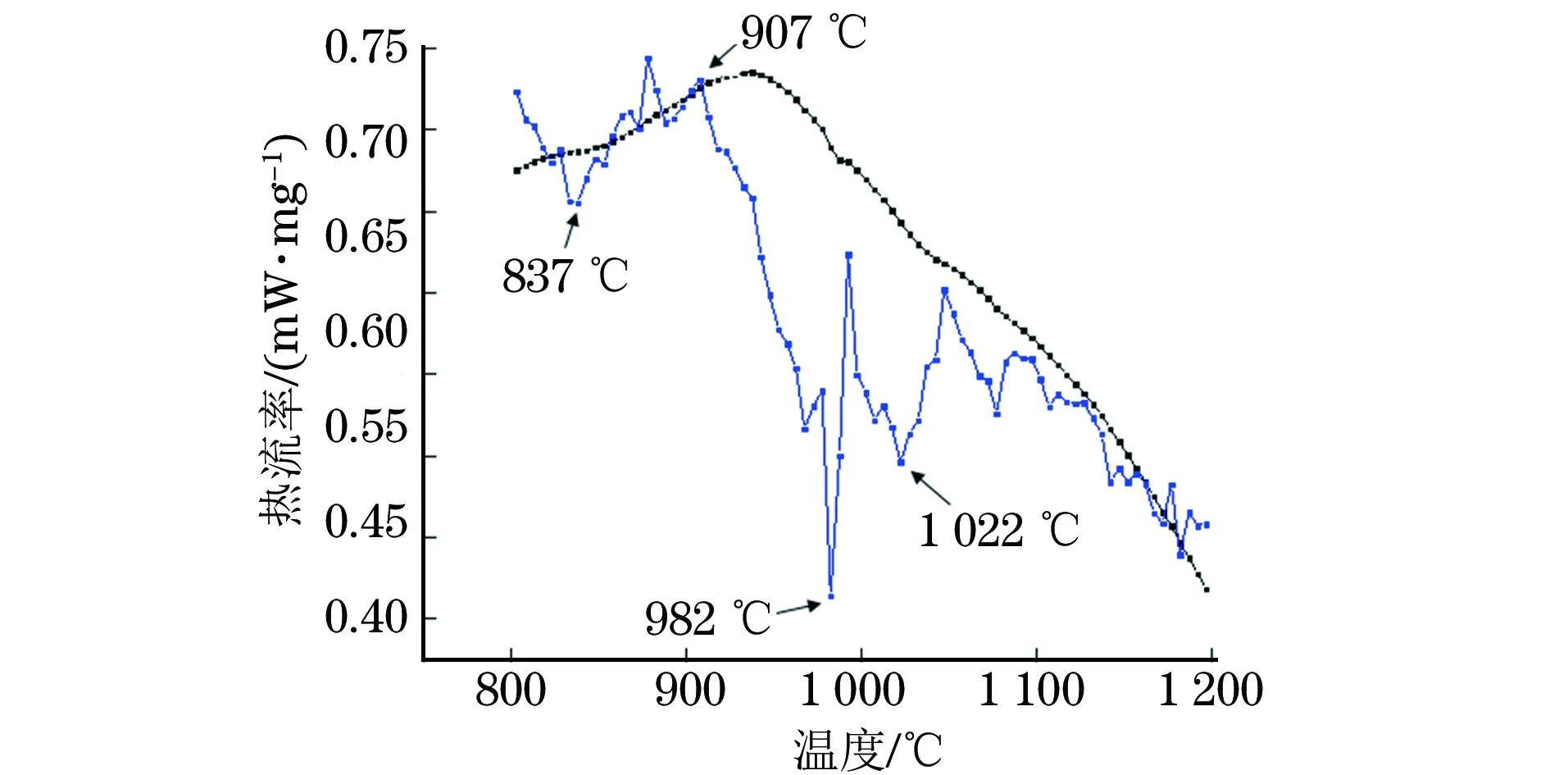
图2 GH4169试样的差热分析

图3 不同固溶温度下试样的微观形貌

2.2 超声特性

2.2.1 背散射信号分析处理

(1) 信号截取与分解计算

以1#试样(固溶温度900 ℃)上的任一采样A扫信号为例，对截取的背散射信号(见图4)进行经验模态分解，图5为这一超声信号的EMD分解结果，其中IMF1～IMF7对应各阶(1～7阶)固有模态函数，Residue(r)表示剩余高阶分量函数。根据式(1)和式(2)分别计算这一超声信号各阶固有模态函数的平均功率和波形维数。

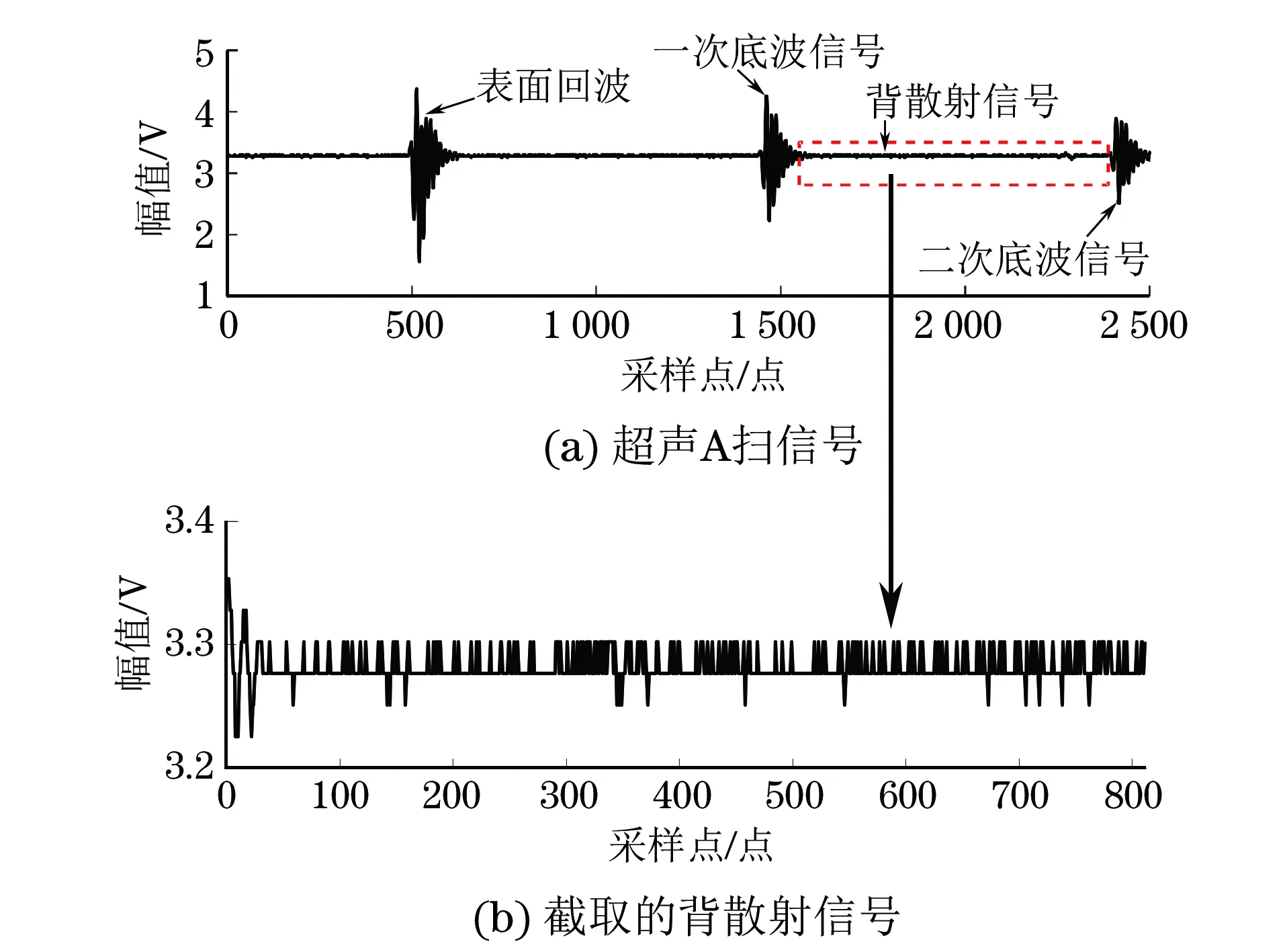
图4 EMD分解的输入信号(以1#试样任一采样点超声信号为例)

(2) 试样超声信号表征值的计算

对任一试样进行多点采样，计算每个采样点A扫信号试样内部组织背散射信号各阶固有模态函数的平均功率、波形维数，并计算其平均值作为该试样的超声信号表征值。

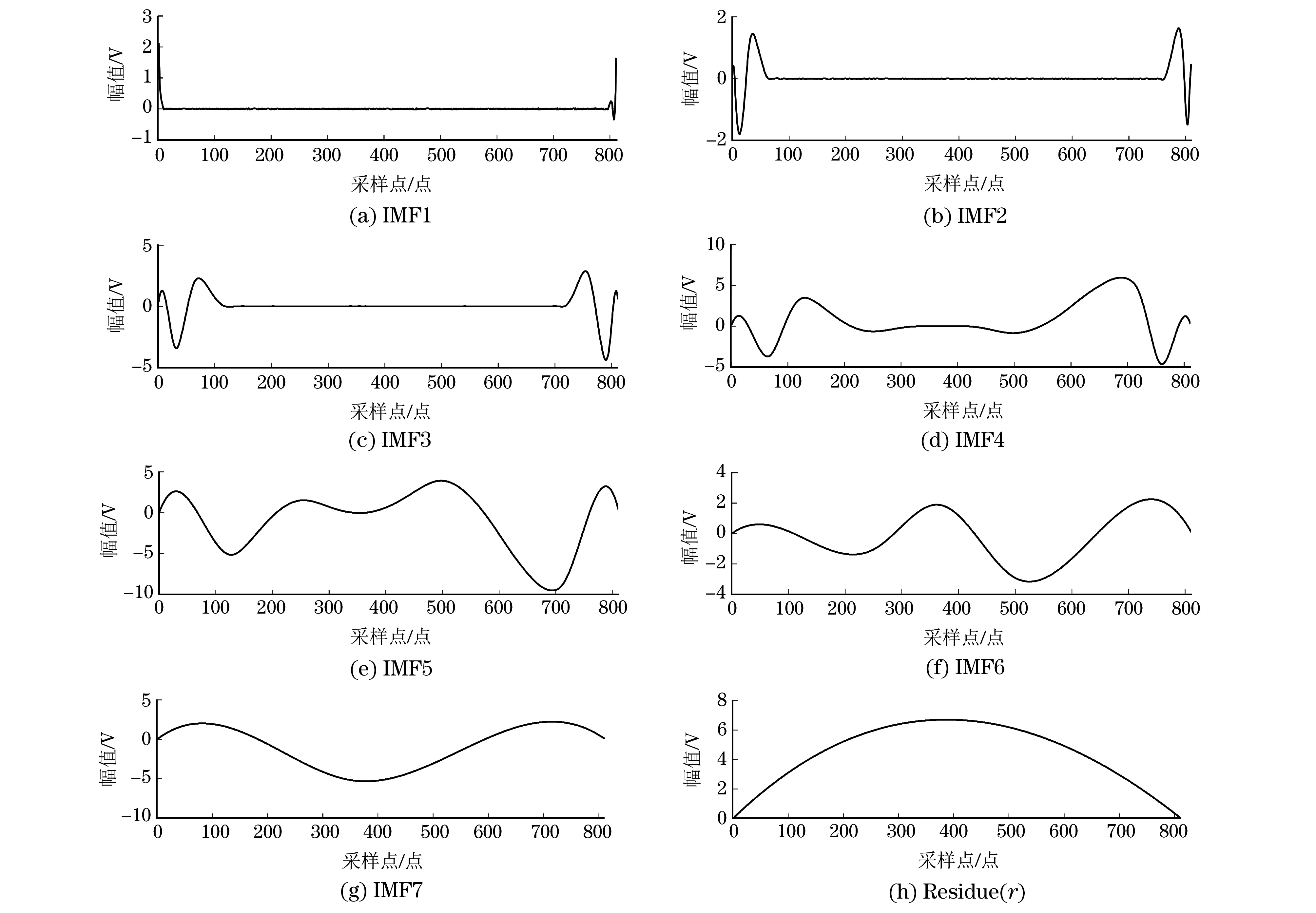
图5 图4中背散射信号的EMD分解结果

(3) 固有模态函数选取

10个不同固溶温度试样对应的IMF1～IMF7的平均功率或平均波形维数与平均晶粒直径或纵横比的Pearson相关系数见表1,2。根据各阶固有模态函数的特征值与被检参数之间的相关性进行函数选取，即选取相关性最为显著的固有模态函数。

表1 各阶模态函数平均功率与晶粒尺寸及形状的相关性

表2 各阶模态函数波形维数与晶粒尺寸及形状的相关性

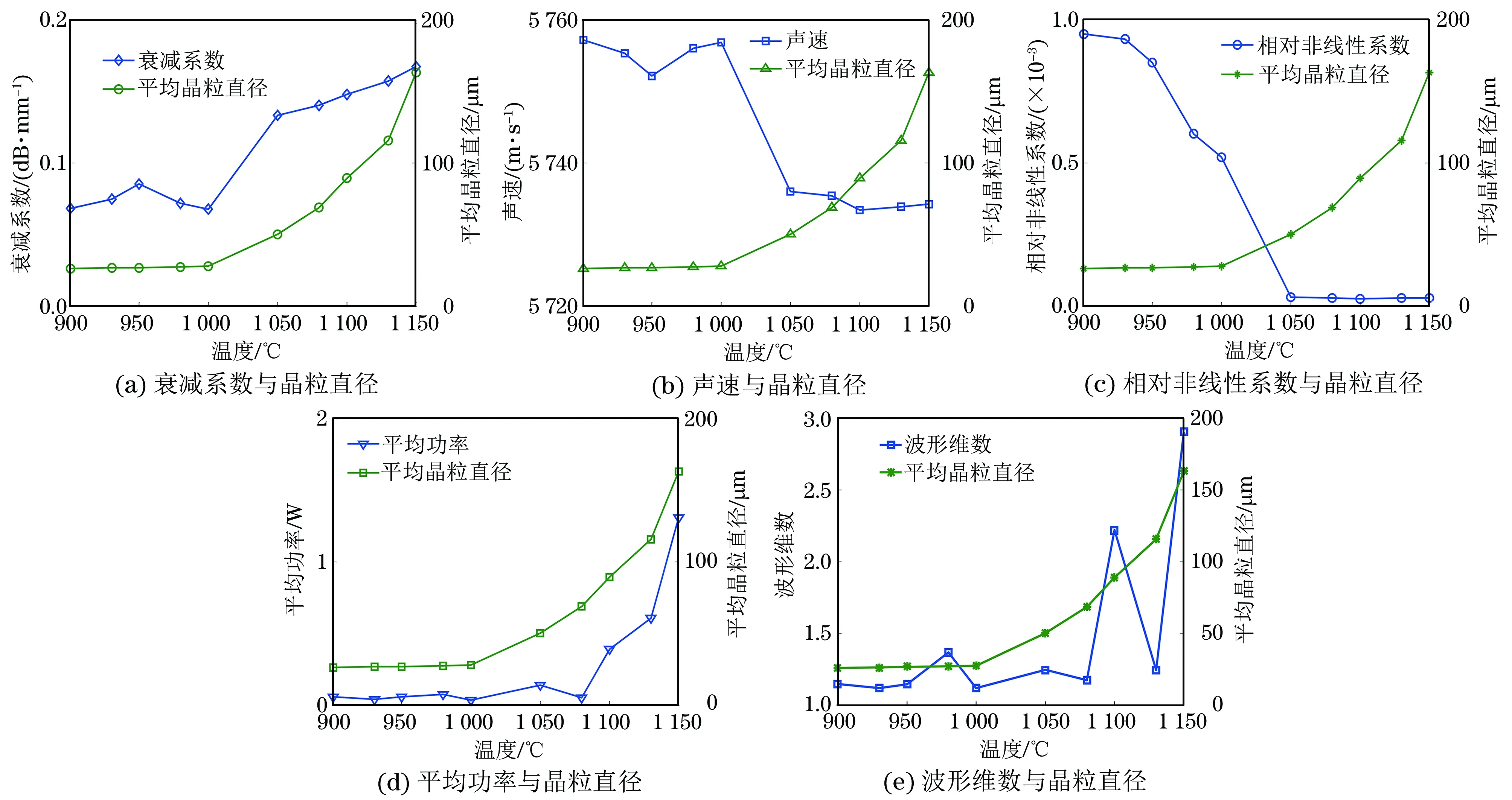
图6 超声特性参数与晶粒尺寸随温度变化的关系

注：**相关性在0.01层上显著；*相关性在0.05层上显著。

分析表1,2中的数据，可知平均功率方面，IMF2与平均晶粒尺寸相关性最显著，Pearson相关性系数高达0.944，且两者随固溶温度变化的曲线如图5所示，这与文献[15]结果一致；波形维数方面，IMF1与平均晶粒尺寸最相关，达到0.797。但是各阶固有模态函数的平均功率和波形维数与晶粒形状表征参数的相关性较弱，并没有显著相关项，这可能与所选取的形状表征参数计算方法有关。以相关性为依据，选取各试样的IMF2信号计算各试样的平均功率表征值，选取IMF1信号计算各试样的波形维数表征值。

2.2.2 微观组织形貌与超声表征值之间的关系

图6为超声衰减系数、声速、相对非线性系数、平均功率和波形维数分别与平均晶粒直径随温度变化的关系；图7为5种超声特性参数分别与平均晶粒纵横比随温度变化的关系。

组织结构方面，δ相完全溶解前后晶粒直径和纵横比呈现明显的阶段性区别。900～1 000 ℃阶段，晶粒直径随着温度的升高缓慢增长，纵横比呈现先下降后上升的变化趋势；1 050～1 150 ℃阶段，由于δ相完全溶解，晶粒直径增长幅度变大；在1 000 ℃和1 050 ℃两点上晶粒平均直径和晶粒平均纵横比呈现跳跃式增长；在1 050 ℃晶粒纵横比达到峰值，随后缓慢下降，并在1 130 ℃以后下降速率增大。

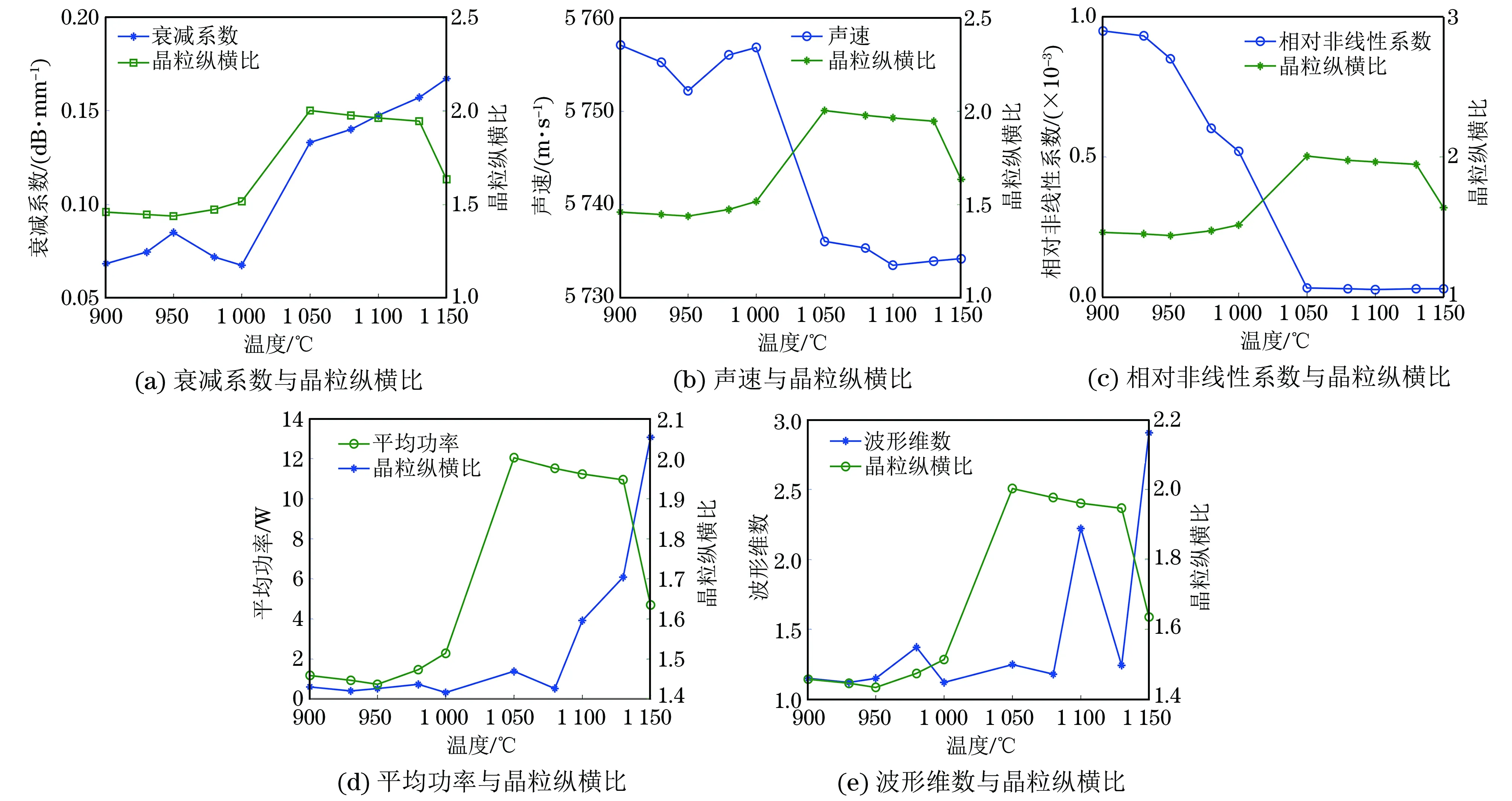
图7 超声特性参数与晶粒形状随温度变化的关系

(1) 晶粒尺寸与超声表征值之间的关系

超声衰减系数、声速和非线性系数均能有效识别出δ相的相变，相变前后有明显阶梯性变化。总体上，衰减系数随晶粒直径的增大而增大，但在950 ℃出现局部极值点，在1 000～1 050 ℃之间出现跃变；相变前声速在5 750～5 760 m·s-1之间，相变后声速在5 730～5 740 m·s-1之间，相变前后两个阶段声速偏差在20 m·s-1。非线性系数在相变先后呈现一个数量级的差异，相变前非线性系数在0.5×10-3～1×10-3之间，其随着温度升高而减小，相变后非线性系数在0.2×10-4～0.3×10-4范围内波动。

背散射信号经过经验模态分解后,IMF2的平均功率随温度的升高而增大，与晶粒平均直径的变化具有明显的相似性，但是在相变前后没有阶段性变化，无法用于识别相变，尤其是在1 080 ℃出现数值下降，与1 000 ℃时计算值相近，易造成识别时的混淆。

IMF1的波形维数与晶粒平均直径之间有显著的相关性，总体上随温度升高而增大，但是在局部范围内出现明显的波动。

(2) 晶粒形状与超声表征值的关系

相变不仅改变晶粒尺寸，对晶粒形状也有明显影响，超声衰减系数、声速和非线性系数与晶粒形状在相变前后有明显差异,如图7(a)～(c)所示。其中，声衰减系数与纵横比变化趋势相反，在950 ℃达到局部极值点，声衰减系数为极小值，晶粒纵横比为极大值，在1 050 ℃之后声衰减系数增加，晶粒纵横比下降。 相变前，声速与晶粒纵横比的变化规律相似，均在950 ℃达到极小值，相变后声速在5 735 m·s-1附近波动，晶粒纵横比则逐渐减小。δ相的含量变化对相对非线性系数影响较大，相变前，非线性系数表现出明显的下降，变化率较大；相变后晶粒粗化对非线性系数的影响较小，非线性系数在0.25×10-4附近波动。

背散射信号经验模态分解后，IMF2的平均功率和波形维数与平均晶粒纵横比之间的相关性较弱，随温度变化的关系曲线上没有表现出明显的相似或相反的变化规律。

3 结论

对不同固溶温度下GH4169合金试样的晶粒尺寸及形状与超声特性的关系进行研究,得出以下结论：

(1) δ相的析出和溶解是影响晶粒尺寸和形状的主要原因。

(2) 采用衰减系数、声速和相对非线性系数能够有效识别GH4169相变前后的不同状态，其中非线性系数对δ相的含量变化敏感，在相变前其随温度升高的变化率较大。

(3) 采用EMD方法对背散射信号进行分解，提取IMF2的平均功率和IMF1的波形维数都可有效表征晶粒尺寸，其中平均功率对晶粒尺寸变化的敏感程度与衰减系数相近，但是两种特征值对相变前后差异的识别能力较差，无法通过数据变化体现δ相的完全溶解。

(4) 采用EMD方法对背散射信号进行分解，提取的IMF2的平均功率和IMF1的波形维数与晶粒纵横比之间的相关性弱。

参考文献:

[1] 师昌绪,仲增墉. 我国高温合金的发展与创新[J]. 金属学报, 2010, 46(11):1281-1288.

[2] TOOZANDEHJANI M, MATORI K A, OSTOVAN F, et al. On the correlation between microstructural evolution and ultrasonic properties: a review[J]. Journal of Materials Science, 2015, 50(7):2643-2665.

[3] VIJAYALAKSHMI K, MUTHUPANDI V, JAYACHITRA. Influence of heat treatment on the microstructure, ultrasonic attenuation and hardness of SAF 2205 duplex stainless steel[J]. Materials Science & Engineering A, 2011, 529(1):447-451.

[6] AGHAIE-KHAFRI M, HONARVAR F, ZANGANEH S. Characterization of grain size and yield strength in AISI 301 stainless steel using ultrasonic attenuation measurements[J]. Journal of Nondestructive Evaluation, 2012, 31(3): 191-196.

[7] VIJAYALAKSHMI K, MUTHUPANDI V, JAYACHITRA R. Influence of heat treatment on the microstructure, ultrasonic attenuation and hardness of SAF 2205 duplex stainless steel[J]. Materials Science and Engineering A, 2011, 529(1): 447-451.

[8] RUIZ A, ORTIZ N, MEDINA A, et al. Application of ultrasonic methods for early detection of thermal damage in 2205 duplex stainless steel[J]. Ndt & E International, 2013, 54(3):19-26.

[9] FREITAS V L D A, ALBUQUERQUE V H C D, SILVA E D M, et al. Nondestructive characterization of microstructures and determination of elastic properties in plain carbon steel using ultrasonic measurements[J]. Materials Science & Engineering A, 2010, 527(16):4431-4437.

[10] ALBUQUERQUE V H C D, SILVA E D M, LEITE J P, et al. Spinodal decomposition mechanism study on the duplex stainless steel UNS S31803 using ultrasonic speed measurements[J]. Materials & Design, 2010, 31(4):2147-2150.

[11] SILVA E D M, ALBUQUERQUE V H C D, LEITE J P, et al. Phase transformations evaluation on a UNS S31803 duplex stainless steel based on nondestructive testing[J]. Materials Science & Engineering A, 2009, 516(1/2):126-130.

[12] 占连扬,刘柯,杨友杰,等. 球墨铸铁QT400-18的石墨球化率对超声声速的影响[J]. 无损检测, 2017, 39(11): 36-38.

[13] 时靖,刘柯,邬冠华,等. 锻造参数对TC4锻件的组织和超声声速的影响[J]. 无损检测, 2017, 39(10): 24-27.

[14] DU Hualong, LONSDALE C, OLIVER J, et al. Evaluation of railroad wheel steel with lamellar duplex microstructures using diffuse ultrasonic backscatter[J]. Journal of Nondestructive Evaluation, 2013, 32(4):331-340.

[15] TITTMANN B R, ABDEL-GAWAD M, FERTIG K. Ultrasonic characterization of microstructure in powder metal alloy[J]. Journal of the Acoustical Society of America, 1984, 76(2): 119-133.

[16] YANG L, LI J, LOBKIS O I, et al. Ultrasonic propagation and scattering in duplex microstructures with application to titanium alloys[J]. Journal of Nondestructive Evaluation, 2012, 31(3): 270-283.

[17] 宋永锋, 李雄兵, 吴海平,等. In718晶粒尺寸对超声背散射信号的影响及其无损评价方法[J]. 金属学报, 2016, 52(3):378-384.

[18] CAI Yeqing, SUN Jinzhong, LIU Chengjie, et al. Relationship between dislocation density in P91 steel and its nonlinear ultrasonic parameter[J]. Journal of Iron and Steel Research(International), 2015, 22(11): 51-57.