弱电网下三相LCL光伏并网逆变器控制策略研究

杨溪源，李彦哲

(兰州交通大学，兰州 730070)

0 引 言

近年来，全球能源紧张和环境污染问题日益严峻，针对太阳能等清洁可再生能源如何采取有效措施充分利用成为人们关注的热点。作为太阳能利用的重要形式，国内外学者将主要目光投入到以并网逆变器为核心的光伏并网发电技术。并网逆变器通过并网点与电网相连，其输出电压被电网钳住，因此在光伏并网系统运行时，光伏逆变器一般采用电流控制的方式，通过控制逆变器的输出电流与电网电压同相位，消除网络谐波，达到最佳并网条件[2]。并网逆变器的脉宽调制(PWM)策略，导致其输出的电压波形中含有大量的开关频率次谐波，为了减少并入电网电流中存在的开关谐波含量，获得正弦度高的并网电流，需要在并网逆变器输出侧选取合适的滤波器[3]。常见的串联滤波器主要有L型和LCL型两种[4]。相比于单L滤波器，LCL输出滤波器增加了电容支路，使其对高次谐波呈现高阻性，对高次谐波的抑制效果更好，且在实现同样滤波效果的前提下，LCL滤波器中两个电感的总电感量之和小于L滤波器中单个电感的电感量，因此耗费的体积更小，成本更低[5]。可是，LCL是没有阻尼的三阶系统，需要更加复杂的控制策略，且光伏逆变器的稳定性会因主电路中产生的谐振受到严重影响[6]。

采用无源阻尼方法，在LCL滤波器中串联或并联电阻R可有效抑制该谐振尖峰。这种方法实现简单，但会给系统带来一定的损耗，并会对LCL滤波器造成影响，如降低滤波器的低频增益，削弱滤波器的高频衰减能力[7]。采用有源阻尼方法，通过修正控制环路上LCL滤波器的频率特性，从而达到预期效果，有效避免这些负面因素。按照类型，有源阻尼法可分为基于滤波器的有源阻尼法和基于状态变量反馈的有源阻尼法，其中基于滤波器的有源阻尼方法通常在控制回路中增加滤波环节[8]，如低通、超前-滞后、陷波器等来增加谐振频率处的稳定裕度，此方法实现简单，但必须确切地知道LCL滤波器的谐振频率。然而在实际应用中，由于磁心饱和、原件老化等因素的影响，LCL滤波器的参数会发生变化，谐振频率也发生变化，在这种情况下，陷波器阻尼的效果会削弱，甚至失效。基于状态变量反馈的有源阻尼方法，是指为了获得与实际电阻相同的阻尼效果，通过反馈适当的电流或电压变量，从控制上模拟虚拟电阻，且不会影响LCL滤波器的特性。其中最常用的为电容电流反馈控制。

由于我国太阳能资源分布的特点，许多光伏电站建在偏远地区，使得光伏电站发出的电必须经过长距离输电才能到达负荷端，长距离输电线路及低功率因数变压器等参数形成的电网阻抗使电网越来越表现出弱电网的特性。当电网阻抗较大时，会改变光伏逆变器控制环路的增益，影响其控制性能，甚至导致并网电流波形出现畸变；且随着光伏发电渗透率的扩大，电网阻抗引起的谐振现象可能严重影响到整个光伏并网系统的稳定运行。文献[9]详细阐述了电网阻抗的产生及对光伏逆变器控制性能的影响。

针对以上问题，本文在考虑电网阻抗条件下，对于LCL型并网光伏逆变器，分析电网阻抗对其电流环控制性能的影响，并且提出了在弱电网下，采用状态反馈极点配置的控制方法，将系统的闭环极点配置到与理想设计时一致，进而消除电网阻抗对并网光伏系统稳定性能的影响，提高系统的动、稳定性以及入网电流的电能质量。通过MATLAB搭建的仿真模型，验证本方法的正确性和可行性。

1 LCL光伏逆变器并网系统

图1三相LCL型光伏并网系统的拓扑结构及控制策略

本文在两相静止坐标系下对入网电流进行控制，Gc(s)为电流调节器传递函数。由于在两相静止参考系下，从结构上看，三相LCL光伏并网逆变器的电路拓扑与两个相同的单相LCL型电路等效。因此，首先分析电网阻抗对单相并网逆变器的影响，进而拓展到三相并网逆变器系统中。

忽略配电变压器和线路上的寄生电阻，考虑电网阻抗条件下的单相并网逆变器结构如图2所示。它由全桥逆变、逆变侧电感L1、网侧电感L2及滤波电容C构成，其中Udc为直流母线电压，uinv为光伏逆变器输出端电压，i1为逆变器侧电流，i2为并网侧电流，iC为电容电流，us和is分别表示电网电压及并网电流，PCC为公共并网点，ug为并网点电压，其值为实际电网电压us与电网阻抗上的压降和。由于电网阻抗中等效电抗的影响要远大于等效电阻[10]，所以这里只考虑感性阻抗Lg。

图2LCL单相并网逆变器

由图2可得电流环控制框图，如图3所示。

图3电流环控制框图

图3中，kPWM为并网逆变器的增益。一般情况下kPWM可表示：

在光伏并网逆变器的电流控制中，比例谐振(以下简称PR)控制器比比例积分(PI)控制器具有更好的稳态性能和抗干扰性能，因此更为适用[11]。为确保PR控制器在电网的基波频率处始终具有较高的增益，本文最终采取可在较宽频带内获得高增益的准比例谐振控制器[12]，以实现两相静止坐标系下无静差跟踪。其表达式如下：

式中：kp为比例系数；kr为谐振系数；ω0=2πf0为基波角频率；ωc为准PR控制器的-3dB截止频率。增大ωc能够使式(2)中的准PR控制器在较宽的频带范围内得到高增益，以降低控制器对频率波动的敏感性。

根据图3的电流环控制框图，可得并网侧电流i2和光伏逆变器输出侧电压uinv以及并网点电压ug之间的关系式，如下：

其中:分母Gq(s)满足下式：

Gq(s)=s3L1(L2+Lg)C+s2kckPWM(L2+Lg)C+

s(L1+L2+Lg)

(4)

电网电压对系统的作用视为扰动，忽略电网阻抗，则光伏逆变器电流控制回路闭环控制系统的开环传递函数表达式：

式中：kc为电容电流反馈有源阻尼系数:

式中：ζ为阻尼比。相关研究表明，ζ越大，阻尼效果越好，但电力系统的稳定裕度会因过大的阻尼比受到影响。工程上，ζ取值在0.5～1之间，一般取折中值0.707。

如上所述，代入数值，计算得出电容电流反馈有源阻尼系数kc=0.017。准PR控制器参数的设计过程参照文献[13]，这里参数给定为kp=0.006，kr=0.5，ωc=π rad/s 。由式(5)知，基于准PR控制的LCL光伏逆变系统的开环传递函数伯德图如图4所示。

图4电流环开环传递函数伯德图

由图4可以看出，在不考虑电网阻抗对光伏逆变器的影响时，光伏并网控制系统开环传递函数的截止频率为 513 Hz，相位裕度为 55°，系统的稳态性能和动态响应良好。

2 电网阻抗对光伏逆变器的影响

电网阻抗主要包括传输线路上的阻抗和配电变压器漏抗[14]，在弱电网中，通常感抗变化较大，近似估算出电网阻抗Lg=0.17 mH。当电网阻抗存在时，根据式(3)和式(4)得到控制系统的等效开环传递函数：

T′=Gc(s)·

当电网阻抗增大时，光伏逆变器电流环开环控制系统的伯德图如图5所示。

从图5可以看出，在考虑电网阻抗后光伏逆变器电流环的截止频率变小，且电网阻抗越大，控制系统的开环截止频率越小，甚至小于7次谐波频率。由此可知：并网光伏逆变器电流环开环截止频率易受电网阻抗的影响而减少，截止频率的减小会导致光伏并网控制系统出现低频振荡，使并网电流波形出现畸变，严重影响并网的电能质量。

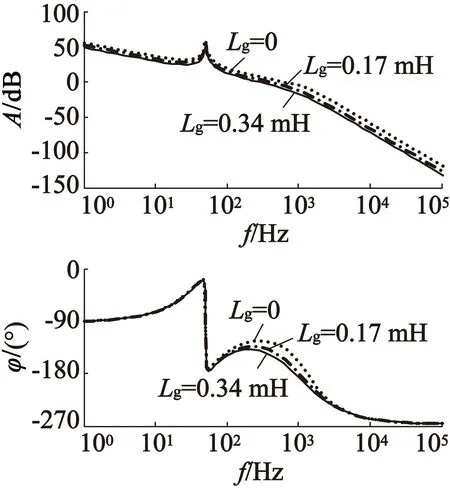
图5电网阻抗对光伏逆变器频率特性的影响

通过以上分析，本文采用极点配置的方法，通过状态反馈实现电流环极点的配置，从而消除电网阻抗对光伏并网逆变器稳定性的影响。

3 基于极点配置的并网电流控制策略

三相LCL光伏并网逆变器的拓扑结构如图6所示。

图6三相LCL光伏并网逆变器

选取状态反馈变量分别为逆变器输出电流i1k，并网电流i2k，电容电压uck，设置状态变量的反馈系数，在无电网阻抗时光伏逆变器系统极点在根平面上的位置上配置控制系统闭环极点，以电流环准PR控制器参数不改变为前提，将控制系统稳定性受电网阻抗的影响进行消除。根据图6，得出光伏逆变器的电流环控制框图如图7所示。其中，可变增益系数为ka，状态变量反馈增益系数分别为k1，k2，k3。

图7基于极点配置的电流环控制框图

图7中，状态变量i1k，i2k，uck(k=a，b，c)与可变增益模块输出电压uik满足如下关系式：

同不考虑电网阻抗时一样，将电网电压作为扰动处理。消去式(8)中状态变量i1k和uck后，I2k(s)与可变增益模块输出Uik(s)关系式：

式中：B=s3L1(L2+Lg)C+s2kPWMk1(L2+Lg)C+

s[L1+(L2+Lg)(1+kPWMk2)]+kPWM(k1+k3) 。

为了消除电网阻抗对光伏并网逆变器稳定性的影响，使有电网阻抗下传递函数G′(s)与无电网阻抗时相同，即式(9)与无电网阻抗时的传递函数式(10)相同。

令G′(s)=G(s)，可得反馈增益系数k1，k2和k3的表达式:

将光伏并网逆变器的参数代入上式，计算出反馈增益系数k1,k2和k3的值后，传递函数G′(s)与无电网阻抗时的开环传递函数G(s)满足下式：

由式(12)可知，只要令可变增益ka满足下式：

即可消除电网阻抗对光伏并网逆变器电流环传递函数的影响。 极点配置后光伏逆变器并网电流的表达式：

综上所述，通过设置状态变量反馈:PWM逆变器的输出电流i1，并网电流i2和电容电压，以实现控制系统极点配置后，电网阻抗对光伏并网逆变器的影响被抑制，从而消除了其对控制系统稳定性的影响。

按照综上设计方法，得到整个光伏并网控制系统的总控制框图，如图8所示。采用极点配置法前后闭环控制系统的开环传递函数的幅频特性曲线，如图9所示。

由图9可知：光伏并网逆变器在弱电网时存在的电网阻抗会降低控制系统电流开环的截止频率，甚至造成系统低频振荡，进而影响系统的稳定性。而采用状态变量极点配置方法后，电流环的截止频率被提高，系统的稳定性增强。

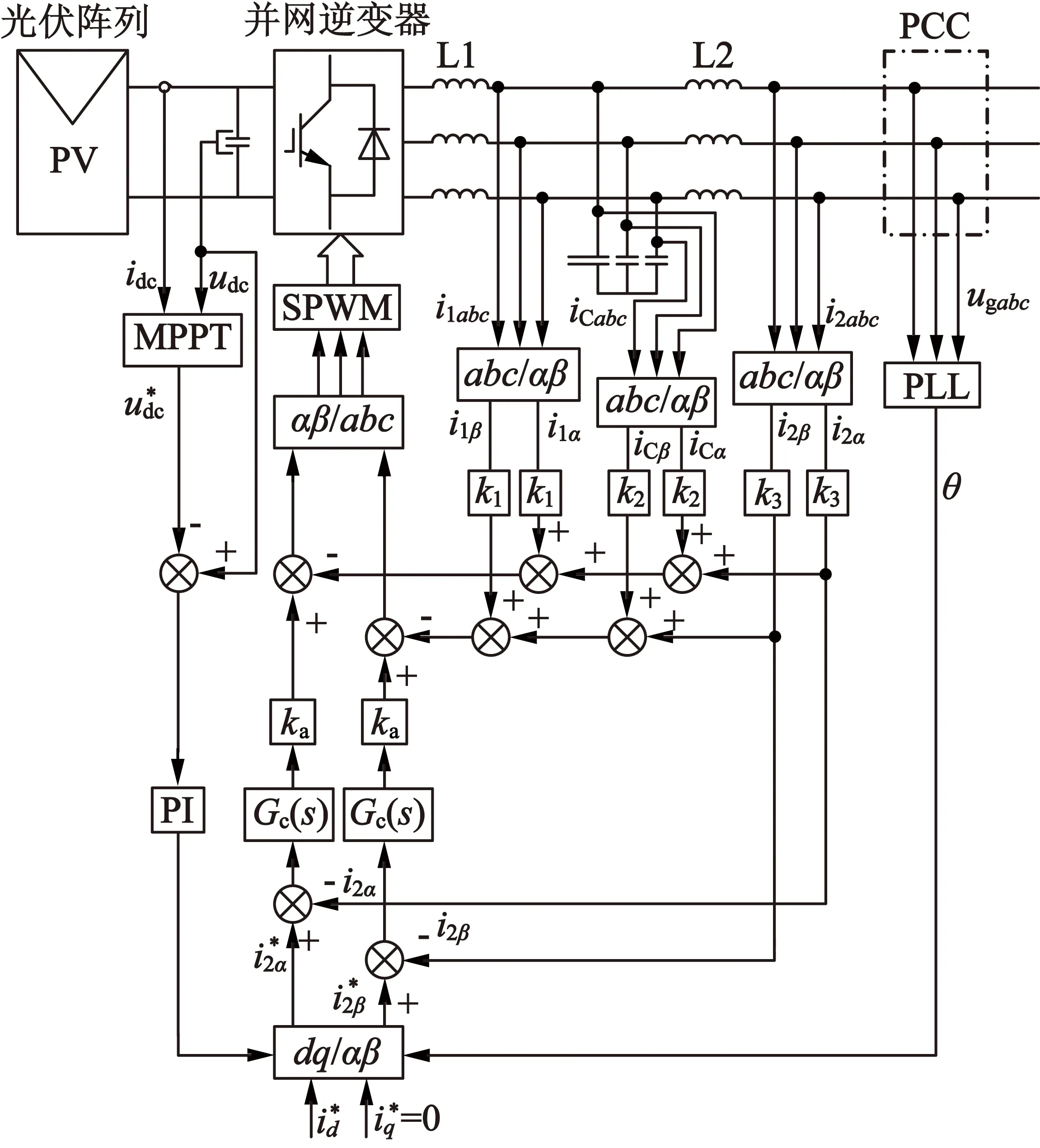
图8基于极点配置的光伏并网逆变器控制框图

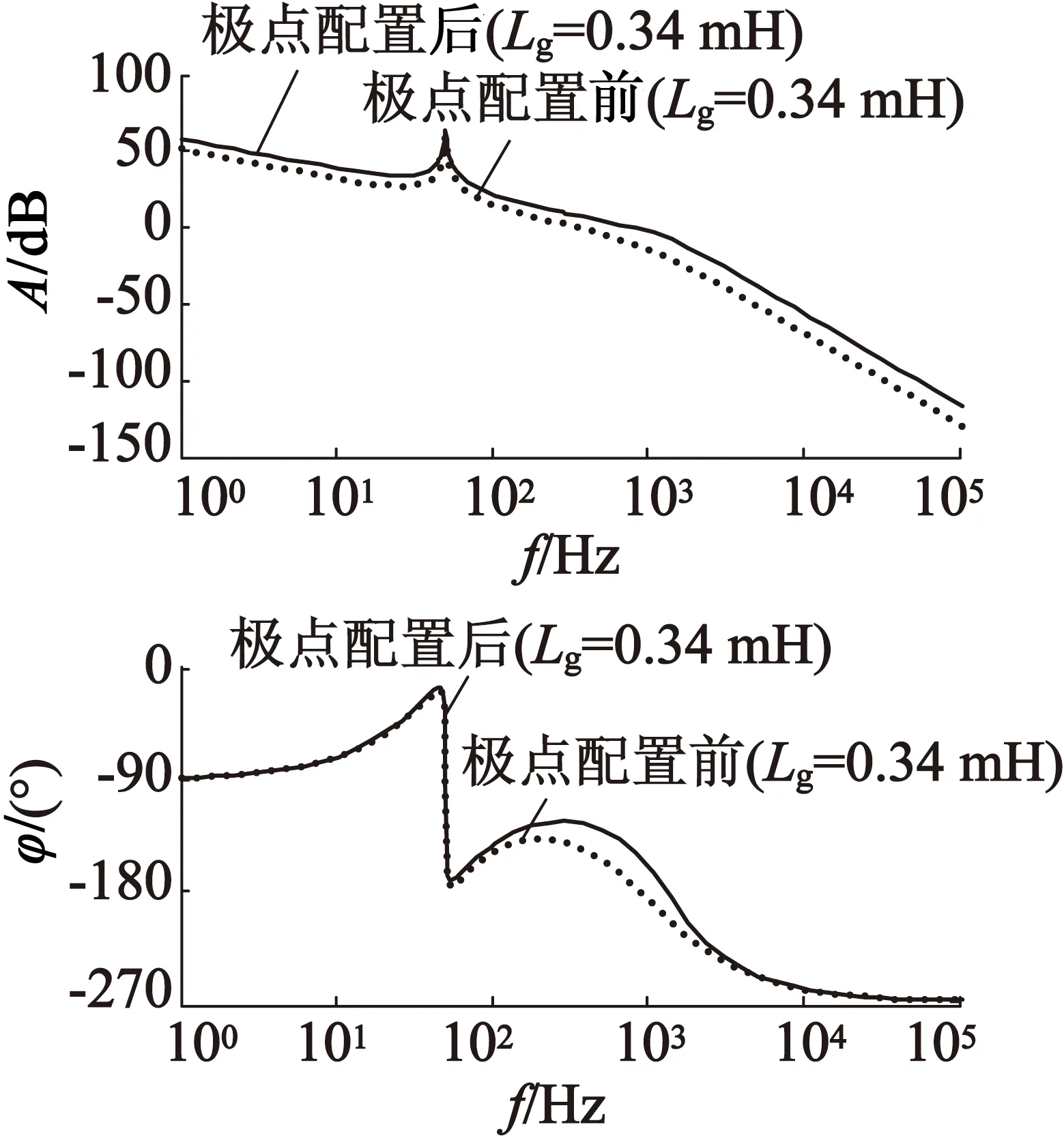
图9极点配置前后控制系统开环传递函数伯德图

4 仿真验证

为了验证本方法的正确性，在MATLAB/Simulink软件中，依据图8的控制策略，搭建200 kW 的三相LCL光伏并网逆变器模型。设置开关频率为10 kHz，直流电压为800 V；LCL滤波器参数：L1=0.48 mH，L2=0.16 mH，C=110 μF；电网阻抗Lg=0.34 mH；准PR控制器参数如前述所示；根据以上参数和式(11)求出k1，k2和k3：k1=0.017，k2=0.006，k3=-0.017。

当电网阻抗存在时，基于准PR控制的光伏并网逆变系统的并网电流i2abc如图10所示。可以看出，当电网阻抗存在时，并网电流波形发生严重畸变，且含有大量的谐波。

图10电网阻抗存在时并网电流的波形图

系统接入电网阻抗且其他参数保持上述设定值不变时，采取状态变量反馈极点配置法后的三相光伏并网逆变器的并网电流i2abc，如图11所示。

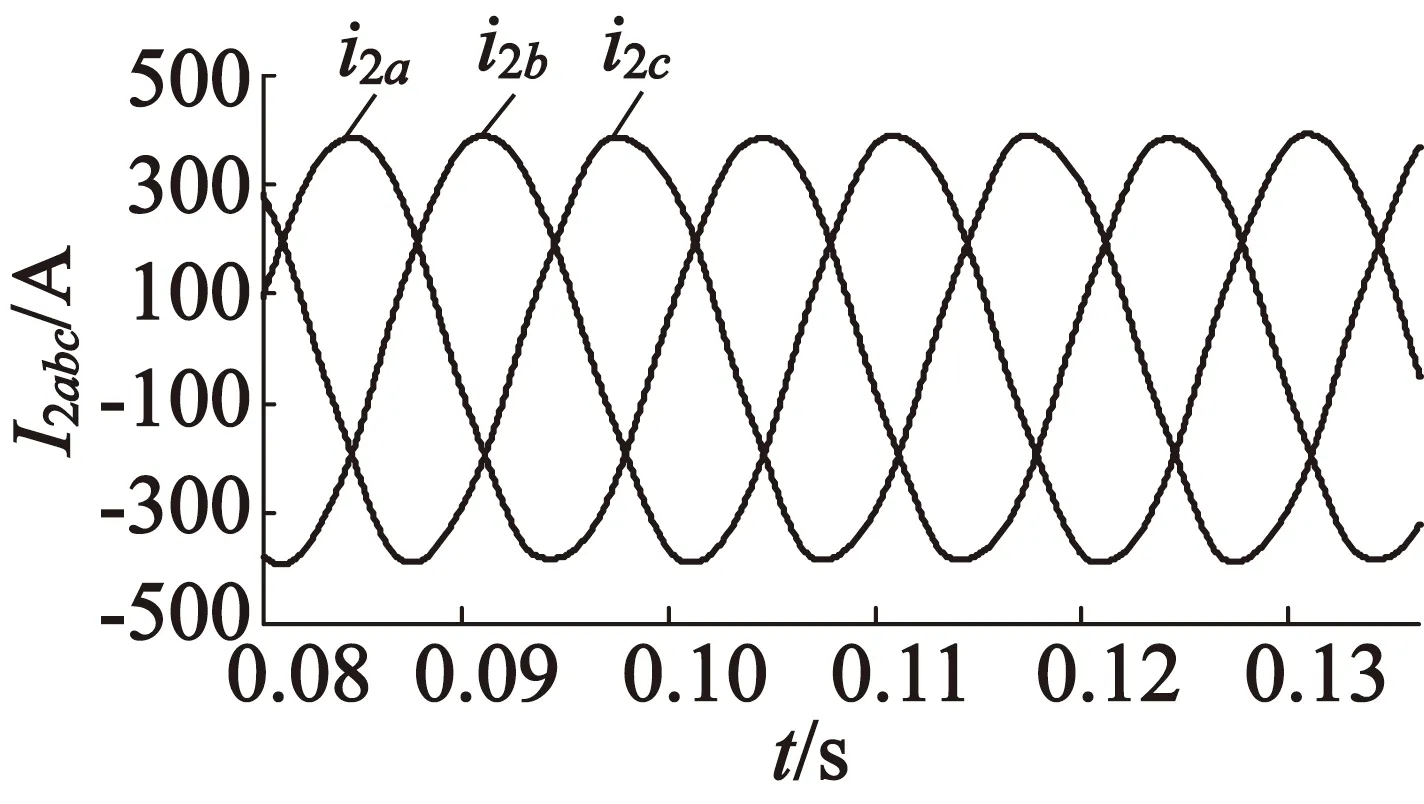
图11接入电网阻抗后并网电流的波形图

由图11可知，采用状态变量反馈极点配置法后，光伏并网逆变器性能良好，且总谐波畸变率THD为0.98%，满足光伏并网的要求。

5 结 语

本文针对并网光伏逆变器控制系统在弱电网情况下的稳定性进行分析，发现电网阻抗的存在会降低控制系统的截止频率，引起系统谐振且并网电流的波形发生严重畸变同时光伏并网的稳定性受到影响。对此，本文利用状态变量反馈的极点配置方法，有效抑制了电网阻抗对三相并网光伏逆变器的影响。仿真结果表明采用极点配置法后，使接入弱电网中的光伏逆变器具有良好的稳定性和波形质量，满足光伏并网的要求。

[1] 曾正，赵荣祥，汤胜清，等.可再生能源分散接入用先进并网逆器研究综述[J].中国电机工程学报，2013，33(24)：1-12.

[2] 赵杰.光伏发电并网系统的相关技术研究[D].天津：天津大学，2012.

[3] 许津铭，谢少军，张斌锋.分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J].中国电机工程学报，2015，35(16)：4153-4166.

[4] 刘飞，徐鹏威，陈国强.基于LCL滤波器的三相光伏并网控制系统研究[J].太阳能学报， 2008，29(8)：965-970.

[5] 王要强，吴凤江，孙力等.带LCL输出滤波器的并网逆变器控制策略研究[J].中国电机工程学报，2011，31(12)：34-39.

[6] 刘韬，郝翔，杨旭，等.LCL滤波的三相并网逆变器电流双环控制策略[J].电源学报，2012(4)：7-12.

[7] 阮新波，王学华，潘冬华，等.LCL型并网逆变器的控制技术[M].北京：科学出版社，2015.

[8] DANNEHL J,LISERRE M,FUCHS F.Filter-based active damping of voltage source converters with LCL filter[J].IEEE Transactons on Industrial Electronics,2011,58(8):3623-3633.

[9] LISERRE M,TEODORESCU R,BLAABJERG F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Transactions on Power Electronics,2006,21(1):263-272.

[10] 李小强，伍小杰，耿乙文，等.感性电网阻抗下三相光伏逆变器稳定性分析[J].中国电机工程学报，2014，34(18)：2906-2916.

[11] 黄如海，谢少军.基于比例谐振调节器的逆变器双环控制策略研究[J].电工技术学报， 2012，27(2)：77-81.

[12] 雷亚雄，李建文，李永刚.基于准PR调节器电流双闭环LCL三相并网逆变器控制[J].电力系统保护与控制，2014，42(12)：44-50.

[13] 孟建辉，石新春，付超.基于PR控制的光伏并网电流优化控制[J].电力自动化设备，2014，34(2)：42-47.

[14] 杨玉琳.弱电网下光伏并网逆变器稳定运行控制技术研究[D].哈尔滨：哈尔滨工业大学，2014.