平稳时序数据的Bootstrap辨识及其改进算法研究
黄雄波
(佛山职业技术学院 电子信息系, 佛山 528000)
0 引言
所谓时序数据,就是将某一物理量在不同时间上的实际观测值,按照时间的先后顺序排列而成的数列。 “平稳”是时序数据的重要特性,它描述了时序数据的数字统计特性是否随着时间的推移而变化,通常,若时序数据的平均功率存在,其均值为常数,且自相关函数与起始时间无关,则称该时序数据为广义平稳时序数据或弱平稳时序数据,简称为平稳时序数据[1-2]。经过众多专家学者的长期研究,平稳时序数据现已形成了一系列成熟可靠的辨识模型及建模方法,以自回归模型(Auto-regressive model,AR)为例,该模型因结构简单且具有高效的参数迭代估计算法,故在实际应用中得到了广泛的应用[3-4]。然而,在现实生活中所获取的时序数据普遍具有非平稳特性,又由于非平稳时序数据尚未有完整和统一的描述方法,据此,人们往往需要对其进行相关的平稳预处理[5-7]后,再采用平稳时序数据建模方法进行后续的辨识。例如,博克思(Box)和詹金斯(Jenkins)于上世纪70年代提出的自回归积分滑动平均模型(Auto-regressive Integrated Moving Average Model,ARIMA),其核心就是通过有限次的差分处理,把原来的非平稳时序数据转化为平稳时序数据[8];黄雄波基于自相关函数理论,对非平稳时序数据中的趋势和周期成分的分离次序和方法作了系统而深入的研究,并得到了一种有效的平稳化转换算法[9];王文华等基于贝叶斯框架对非平稳时序数据的分段平稳问题作了更为深刻的研究,并推导出具有递归关系的高效建模算法[10];张海勇等基于经验模态分解法(Empirical mode decomposition, EMD)把待处理的非平稳时序数据分解成有限个基本的模式分量,然后分别为这些模式分量建立时变的AR模型,进而得到一种新的非平稳时序数据的自回归模型分析方法[11-12]。
为了改善自回归模型的辨识精度并给出相应的置信空间,近年来,国内外一些专家学者开始将Bootstrap方法应用到平稳时序数据的自回归辨识过程中。例如,轩建平等基于小样本统计的 Bootstrap 方法,对车削振颤自回归模型参数的方差进行了估计,从而较好地解决了机床故障诊断中所需的大量样本和重复多次试验的难题[13];杨晓蓉等在单位根存在的条件下,证明了自回归模型所构造的单位根检验统计量的极限分布,可以通过对最小二乘残差进行Bootstrap重抽样方法来逼近[14]。目前,基于Bootstrap方法的自回归辨识算法在实际应用中还存在着一些问题,据此,本文拟设计相应的改进算法予以解决,并以相关的实验来证明改进算法的有效性和先进性。
1 问题描述
时序数据辨识的过程就是对序列的数字统计特征及其分布的不确定性进行评价,在实际的辨识过程中,我们可以采用先验知识、概率模型、可能性及置信区间等来求解不确定关系的表达式或者对其进行估计。然而,在大多数情况下,由于我们并不掌握待分析序列的总体分布,故很可能会得到错误的辨识结果。为克服因样本数量不足而引起的分布估计误差,一种有效的方法就是重抽样,即通过某种模型对原序列进行反复采样,使得原序列容量得到扩充,从而可以较为准确地估计某一统计量的标准差、均值及概率分布等。
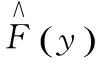
(1)
式(1)中,n为样本长度,N(y)指时间y发生的总次数。
如图1所示。

图1 基于Bootstrap方法的自回归辨识的算法流程图
基于Bootstrap方法的自回归辨识其核心思想就是对残差序列进行m次重抽样,然后构造出一系列的Bootstrap序列,通过对这些残差序列进行参数估计,并用所得的参数均值来修正原有的自回归模型。
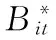
2 改进算法的设计与实现
针对上述问题,本文拟对原有算法作如下改进:(1) 以自回归模型的阶数为Bootstrap的作用范围区间,对残差序列进行重抽样处理;(2) 基于矩阵奇异值的迭代分解理论,对Bootstrap序列的参数进行求解。
2.1 改进的Bootstrap序列生成算法
在理想化的情形下,利用自回归模型对平稳时序数据进行辨识,其剩余的残差序列Et应为一白噪声,即Et~N(0,σ2)成立。然而,由于数据污染和计算误差等原因,残差序列Et往往不能被白化,其各时刻之间的取值仍然存在着某种的统计关联性。据此,在Bootstrap重抽样的过程中,其作用范围区间不应在整个序列内进行,而应以自回归模型阶数p作为滑动窗口的宽度,对残差序列Et进行重抽样,以便保持既有的相关性。根据上述的分析,可设计一种改进的Bootstrap序列生成算法。
算法1:保持既有相关性的Bootstrap序列生成算法
输入:残差序列Et,自回归模型阶数p;
步骤1:用Random()函数在1~n(n为序列的长度)中产生一个随机整数R;
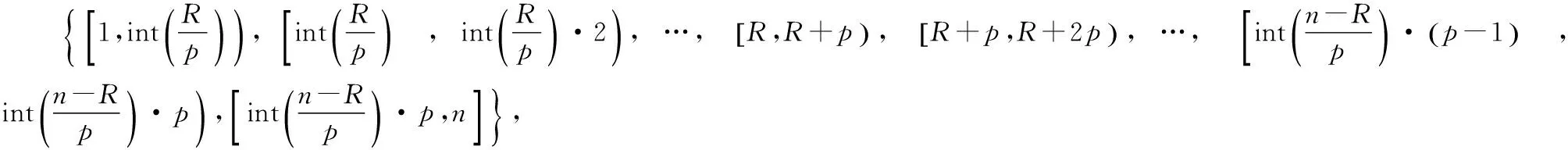
步骤3:应用Bootstrap方法独立地对步骤2中的各个子空间中进行重抽样处理;
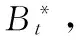
2.2 改进的Bootstrap序列估参算法
Bφ=b.
(2)
式(2)中,
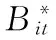
(3)
奇异值分解方法是最小二乘问题的有效求解方法,该方法的主要优点是处理病态和不相容线性方程组的能力强、运算过程中不放大误差且具有良好的稳定性;而缺点就是运算量大。据此,这里拟引入矩阵奇异值分解方法对Bootstrap序列的自回归模型参数进行求解,同时,为了克服运算量大的问题,还需要对奇异值分解方法进行如下的迭代计算改进。
设B(B∈R(n-1-p)×P,n>2p+1)的奇异值分解为式(4)。
(4)
其中,U=[u1,…,un-1-p]和V=[v1,…,vp]是正交矩阵,∑r=diag(σ1,…,σr),σ1≥…≥σr>0。根据矩阵Moore-Penrose广义逆的定义,式(2)的最小二乘解为式(5)。
(5)
为了能使用迭代法对系数矩阵B进行奇异值分解,可以运用Householder变换求得正交矩阵U,V,从而实现系数矩阵B的二对角化,即式(6)。
(6)
其中,
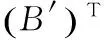
1) 初始化:
①k=1;


④c=α1-μ;
⑤d=β1;
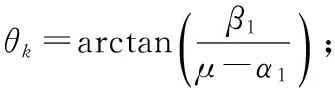
2) 求解如下的矩阵方程,得到奇异值σk:
3)k=k+1,求解如下的矩阵方程,更新θk:
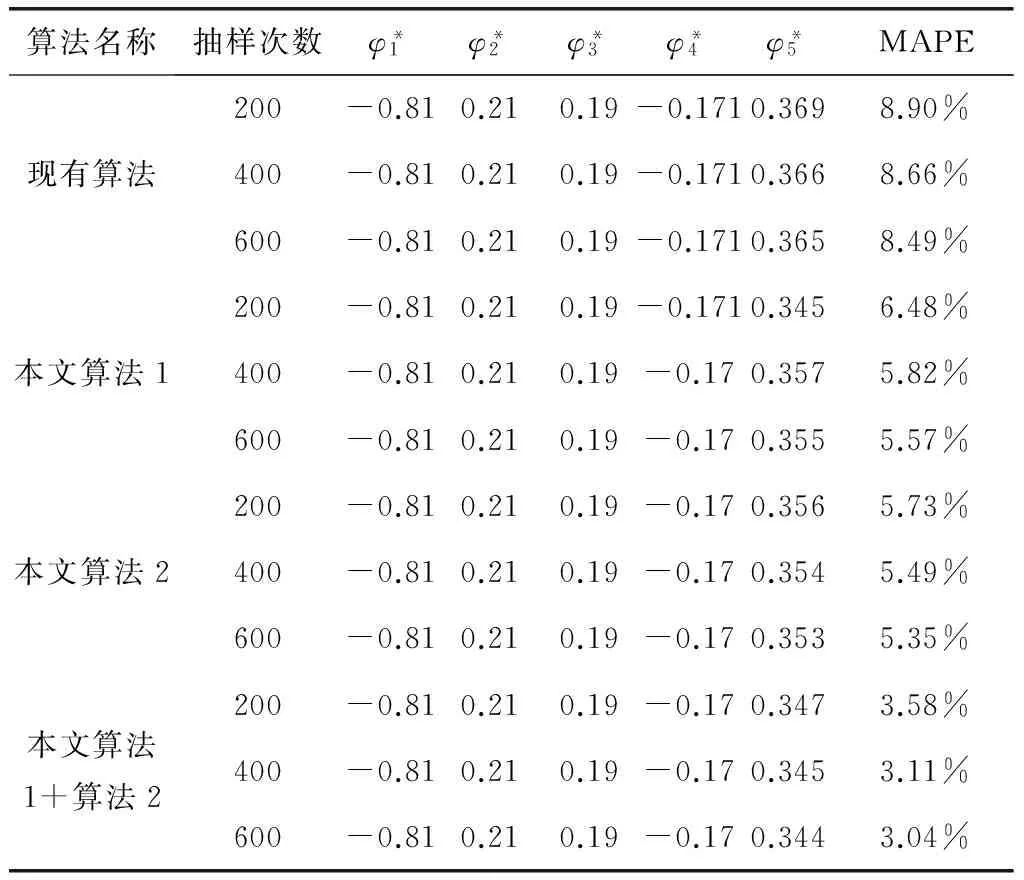
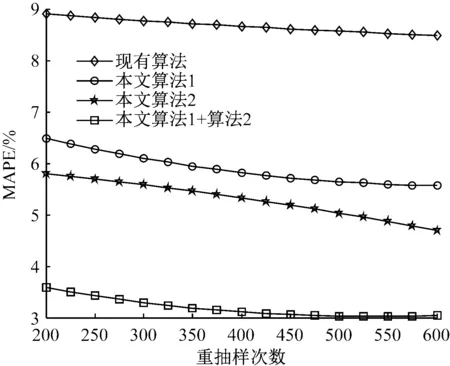
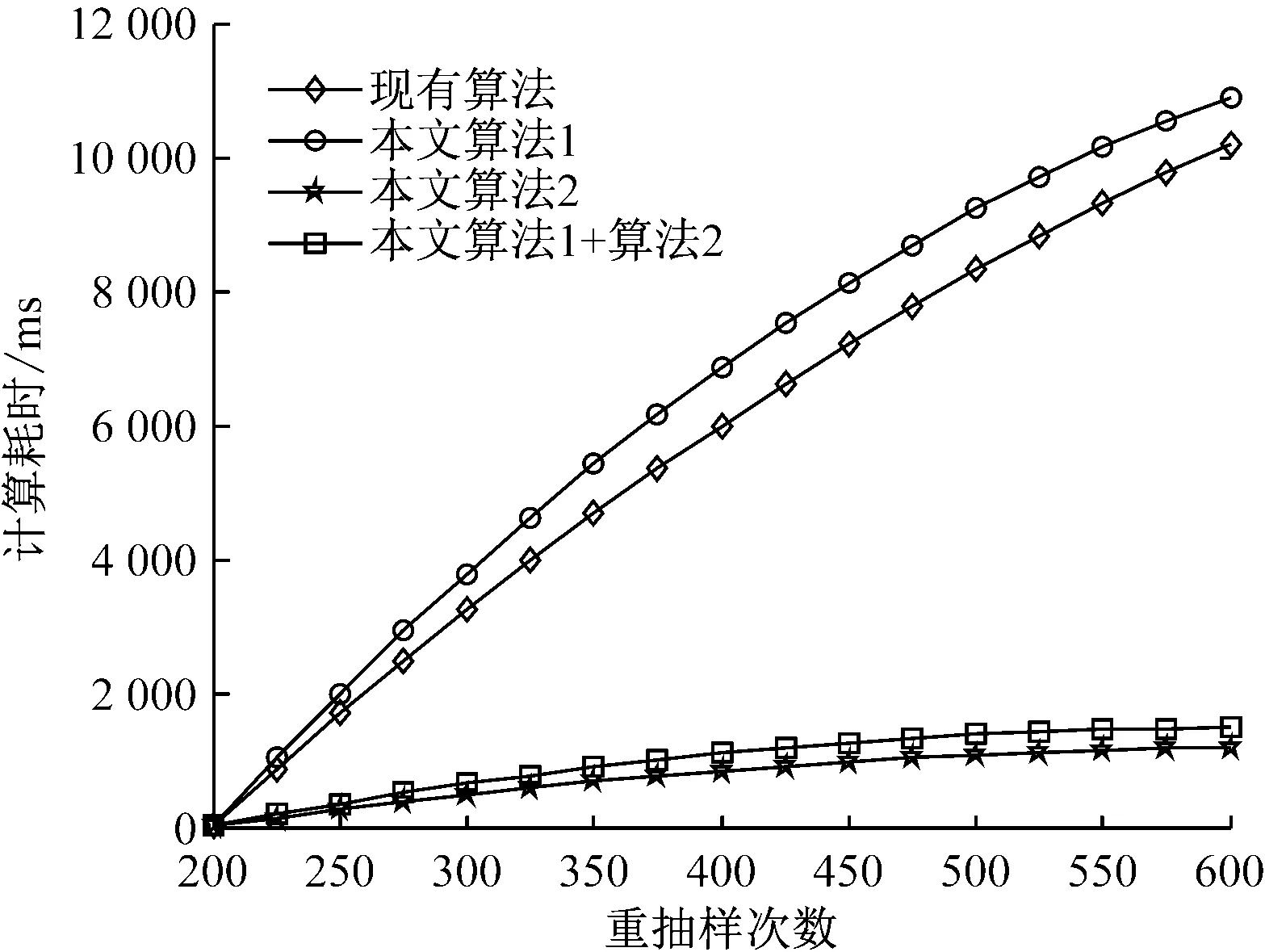
4) 若k 综上所述,可设计如下的Bootstrap序列的估参改进算法。 算法2:基于奇异值迭代分解的Bootstrap序列估参算法 步骤2:对步骤(1)中的线性方程组的系数矩阵施行Householder变换,求得对应的正交矩阵U,V,把系数矩阵B化为式(6)所示的二对角化矩阵B′; 为了验证上述改进算法的有效性及先进性,这里选取了一个自回归仿真模型来进行相关的Bootstrap重抽样辨识。实验在PC机上进行,其硬件配置为,Intel 酷睿i5 4570四核CPU、Kingmax DDR3 16GB RAM、Western Digital 500G Hard Disk;操作系统与开发环境为,Microsoft Windows 10、Microsoft Visual Studio 2010集成开发环境中的C++。在实验过程中,着重关注改进算法的辨识误差和计算开销等技术指标的改善情况,并对相关结果加以详细的分析和讨论。 实验选用了一个五阶的自回归仿真模型,具体数学模型如式(7)。 yt=-0.81yt-1+0.21yt-2+0.19yt-3-0.17yt-4+0.33yt-5+zt. (7) 式(7)中,zt为服从标准高斯分布的白噪声。 基于MATLAB软件中,利用randn()随机数发生函数和filter()数字滤波器函数为式(7)所示的模型生成长度为600的样本序列。首先基于Burg算法对式(7)的模型进行辨识,然后分别应用现有的自回归模型Bootstrap辨识算法、本文算法1、本文算法2及本文算法1+算法2对残差序列进行辨识,并在{200,250,300,…,600}等不同抽样次数的情形下,比对各种算法的辨识精度和辨识耗时的性能表现。 实验过程中,为了客观准确地评价各种算法的辨识精度,这里以式 (8)所示的平均绝对百分误差(Mean absolute percent error, MAPE)作为评价指标,对各种实验组合的辨识精度进行评价。如式(8)。 (8) 用Burg算法对式(7)所示的模型进行辨识,其结果如式(9)所示,于是,便可得到式(10)所示的残差序列Et如式(9)、(10)。 (9) (10) 分别用现有算法、本文算法1、本文算法2及本文算法1+算法2对残差序列Et进行自回归辨识,取每次重抽样其辨识参数的均值与式(9)中对应参数进行叠加求和,从而实现对原Burg算法辨识模型的修正。实验所得的最终辨识参数如表1所示。 表1 各种算法所得的最终辨识参数 而各种算法的MAPE与重抽样次数的关系则如图2所示,限于篇幅,这里仅列出抽样次数为200,400,600共3种情况。 图2 各种算法的MAPE与重抽样次数的关系 从表1可以发现,由于本文算法1在重抽样的过程中保持了残差序列之间既有的相关性,故其辨识精度较现有算法有了3%左右的提升;同样地,基于奇异值迭代分解法的本文算法2因其数值计算更为精确,相应地,辨识精度较现有算法也有了一定的提升。而本文算法1+算法2则是融合了两种改进算法的优点,在保持残差序列之间既有相关性的同时,其估参过程中所产生的计算误差也得到了较好的控制,故其对应的辨识精度也是最高的。如图2所示。 MAPE与重抽样次数之间的关系则表明,各种算法的重抽样次数越多,其辨识精度也就越高,但当重抽样次数达到序列长度的2/3 (400次)之后,辨识精度的提升效果便不再显著,究其原因是因为此时的重抽样操作已基本覆盖了残差序列的未知分布。 各种算法的计算耗时,如图3所示。 图3 各种算法的计算耗时 从图3可以得知,本文算法1花费的计算耗时最多,现有算法次之,本文算法1+算法2排第三,而本文算法2则为最小。 以实验中的模型为例,现有算法的每一次Bootstrap过程,均需要花费一定的时间进行重抽样并生成Bootstrap序列,而且还需基于最小二乘法求解一个行数和列数分别为600和5的线性方程组,以便估算出对应的自回归模型参数φ。实验表明,现有算法的计算耗时主要是消耗在求解高度不相容线性方程组的过程中,据此,其计算耗时与重抽样次数也就存在着明显的线性关系。由于本文算法1的Bootstrap重抽样过程较现有算法复杂,且自回归模型参数φ的求解方法又与现有算法相同,故其计算耗时在略高于现有算法的同时又与其有着相同的特征。相对地,本文算法2基于奇异值迭代分解法改进了自回归模型参数φ的求解过程,故其计算耗时有了大幅度的减少,并表现出对重抽样次数具有良好的负载能力,即计算耗时不随重抽样次数的增加而显著增加。而本文算法1+算法2的计算耗时在略高于本文算法2的同时,却能保持着本文算法2的良好特性。 综上所述,本文算法1+算法2在结合了两种改进算法的基础上,其计算精度和计算耗时均较现有算法有了显著的提升。 对现有的基于Bootstrap方法的自回归模型辨识算法, 进行了两点有意义的改进,改进后的算法具有更优异的辨识性能指标。下一步的主要工作有,研究更为合理的Bootstrap重抽样约束机制,同时,也需要研究并行的奇异值迭代分解法,以便进一步提升算法的适用范围和计算性能。 [1] 克西盖斯纳,沃特斯,哈斯勒.现代时间序列分析导论[M].张延群,刘晓飞,译.北京:中国人民大学出版社,2015. [2] 冀振元.时间序列分析与现代谱估计[M].哈尔滨:哈尔滨工业大学出版社,2016. [3] 黄雄波,胡永健.利用自回归模型的平稳时序数据快速辨识算法[J/OL,网络优先出版].计算机应用研究,2018,35(9). [4] 苏志铭,陈靓影.基于自回归模型的动态表情识别[J]. 计算机辅助设计与图形学学报,2017, 29(6):1085-1092. [5] 王宏禹,邱天爽,陈喆.非平稳随机信号分析与处理(第2版)[M]. 北京:国防工业出版社,2008. [6] 王宏禹,邱天爽.非平稳确定性信号与非平稳随机信号统一分类法的探讨[J]. 通信学报,2015, 36(2):2801-2810. [7] 王宏禹,邱天爽.确定性信号分解与平稳随机信号分解的统一研究[J]. 通信学报,2016, 37(10):1891-1898. [8] 博克思,詹金斯,莱因泽尔.时间序列分析:预测与控制(第4版)[M].王成璋译.北京:机械工业出版社,2011. [9] 黄雄波.基于自相关函数的非平稳时序数据的辨识改进[J]. 微型机与应用,2016, 35(13):10-14. [10] 王文华,王宏禹.分段平稳随机过程的参数估计方法[J]. 电子科学学刊,1997, 19(3):311-317. [11] 张海勇,马孝江,盖强.一种新的时变参数AR模型分析方法[J]. 大连理工大学学报,2002, 42(2):238-241. [12] 张海勇,李勘.非平稳随机信号的参数模型分析方法[J]. 系统工程与电子技术,2003, 25(3):386-390. [13] 轩建平,史铁林,杨叔子. AR模型参数的Bootstrap方差估计[J]. 华中科技大学学报,2001, 29(9):81-83. [14] 杨晓蓉.自回归时间序列的极限理论及其应用[D].浙江大学博士学位论文,2008. [15] 徐礼文.复杂数据的bootstrap统计推断及其应用[M].北京:科学出版社,2016. [16] James W.Demmel.应用数值线性代数[M] 王国荣译.北京:人民邮电出版社,2007. [17] 徐树方.数值线性代数(第二版)[M].北京:北京大学出版社,2013.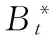
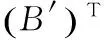
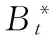
3 实验及结果分析
3.1 实验过程与方法
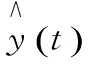
3.2 实验的结果与分析
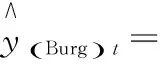
4 总结

