精英遗传改进的非线性灰色神经网络算子与军费开支多目标组合预测应用

张 侃, 刘宝平, 黄 栋

(海军工程大学装备经济管理系, 湖北 武汉 430033)

0 引 言

军费是军队建设资源的总分配器,是军队保障力、战斗力得以生成和维系的源泉[1]。当前,军费开支预测成为炙手可热的研究领域,得到了各国学者的广泛关注。军费开支作为国家财政收入的一项主要的非生产性支出[2],属于宏观经济数据范畴,与国家经济发展水平密切相关。按照现代计量经济学理论,将复杂经济系统中具有时序性特点的军费开支作为国防经济研究领域的重要经济变量,容易受到环境噪声的随机扰动而呈现出非平稳非线性的数据信息特征,使得古典假设条件失效,并引发数据观测失真和预测误差放大等负面效应。为有效消除这些负面效应,通常需要结合协整检验、参数诊断与波动模型[3]等理论工具进行经济数据动态特征追踪与描述。

对军费开支预测而言,由于各种计量模型的建模机理不同,某个计量模型只能够从某特定角度来对军费开支数据信息进行呈现和归集,其预测结论的有效性有待加强。而组合预测的出现,鉴于其在综合性信息的科学选择与统筹使用中的突出优势,则为更好地提高军费开支预测精度,避免预测失灵提供了新的思路。一般研究认为,提高组合预测模型精度需要从两个方面入手:一是需要对组合结构中的基础模型进行理论深化,利用残差数据[4-7]来挖掘原始模型中遗漏的有用信息,进而提高基础模型的预测适应能力;二是需要进一步优化组合预测模型算法[8-11],减少预测的总体不确定性,提高组合预测目标值的整体预测精度。当前,国内外学者在传统组合预测模型的基础上,通过基础模型优化、组合算法改进等多种手段,拓展和演化出新的组合预测模型与方法,取得了广泛的研究成果[12-14]。本文选择军费开支预测作为研究切入点,将精英遗传算法(elitist genetic algorithm,EGA)与组合预测理论相结合,引入非线性灰色神经网络算子,对具有随机波动特征的基础预测模型时序样本残差进行信息提取和分析,提高整体预测精度。与此同时,本文还考虑军费开支组合预测目标的多样化问题,拟通过探讨多种预测目标下的预测结论并对比传统建模预测方法,结合实证分析证明本文所建模型的优越性。

1 预备知识

灰色神经网络算子由灰色理论[15]与人工神经网络理论交叉结合产生,其常用形式为灰色神经网络(grey model back propagation neural network,GM-BP)算子。该算子旨在通过GM(1,1)或GM(1,N)方法弱化时间序列数据随机性来组织建模过程[16-20],而BP神经网络[21-22]作为多层前馈神经网络的经典代表,蕴含了神经网络最精华、最完美的核心内容,能够利用非线性映射处理不规则、混沌特征的数据序列,但存在解决单纯GM模型建模过程中数据自适应能力偏弱,自主学习能力较低的问题。两者算法结合优势互补,能够解决诸多实际问题。尽管如此,算子中GM部分在形式上仍为线性模型,利用该算子对非平稳数据呈现的残差非线性特征进行描述,在高精度条件下是无法满足要求的。因此,本文采用一种适应性更强的非线性灰色神经网络算子,该算子能够有效描述S型非线性序列特征,即G-Verhulst-BP(grey Verhulst BP neural network)算子。

定义1设Y=(y(1),y(2),…,y(n))是一个非平稳时间序列,记为Y={y(t),t=1,2,…,n},∀y(t)∈y⟹t∈T={1,2,…,n},若存在t*∈T,有y(t*)>y(t),t∈{1,2,…,t*-1}∪{t*+1,t*+2,…,n},则称Y为以y(t*)为峰点的非平稳单峰序列。

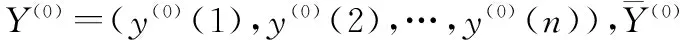
η(0)=(η(0)(1),η(0)(2),…,η(0)(n))

(1)

η(1)=(η(1)(1),η(1)(2),…,η(1)(n))

(2)

Z(1)=(z(1)(1),z(1)(2),…,z(1)(n))

(3)

称模型η(0)(t)+az(1)(t)=b(z(1)(t))α为非线性残差灰色幂模型,记为GM(1,1,α);当α=2时,称η(0)(t)+az(1)(t)=b(z(1)(t))2为非线性残差G-Verhulst模型,其中,a为发展系数；b为灰色作用量。

定义3将定义2中序列η(0)的前s(1≤s≤n)个数据记为(G-Verhulst)s,若要求建立非线性残差G-Verhulst模型的数据下限个数为m(m≤n),则可建立的模型个数为n-m+1个,分别记为(G-Verhulst)m,(G-Verhulst)m+1,…,(G-Verhulst)n,其共同构成的模型组称为(G-Verhulst)m～n模型组。

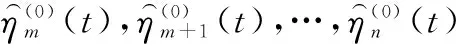
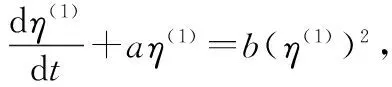
证明由灰色理论知识,仿照GM(1,1)的白化模型与定义型关系,容易得到非线性残差G-Verhulst白化模型与定义式的关系。下面重点证明非线性残差G-Verhulst模型白化响应式。

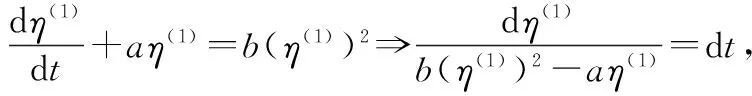
左边按部分分式分解,得

故有

(4)

(5)

取t0=1,t=t′+1, 有

(6)

证毕

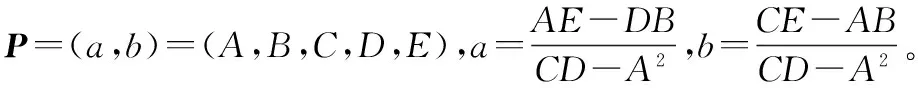
证明G-Verhulst模型定义式η(0)(t)+az(1)(t)=b(z(1)(t))2,以t=2,3…,n中的η(0)(t),z(1)(t)代入有

η(0)(2)+az(1)(2)=b(z(1)(2))2

η(0)(3)+az(1)(3)=b(z(1)(3))2

⋮

η(0)(n)+az(1)(n)=b(z(1)(n))2

整理后有

η*=GP

(7)

(8)

由最小二乘准则得

P=(GTG)-1GTη*

(9)

(10)

(12)

证毕

定理3对于任何在闭区间内一个连续函数都可以用单隐层的BP网络逼近,故一个3层BP网络可以任意精度逼近任何一个非线性映射(该定理参考文献[23],证明略)。

2 军费开支多目标组合预测原理

2.1 问题描述

假设某国军费开支可由m种不同基础模型分别进行预测。由定义1知,Y={y(t),t=1,2,…,n}为n维实际观测值,令fi(t)为由第i种基础模型预测得到的第t个预测值,σi为第i种基础模型的权重,Ei(t)=y(t)-fi(t)为第i种基础模型预测得到的第t个预测值的残差。由m种计量模型构成的计量组合预测模型为

(13)

式中,E(t)为m种基础模型组合预测得到的第t个预测值的残差。

2.2 常用评价准则的多目标组合

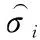
(14)

minφ=φ(S1,S2,S3)

1≥σi≥0

i=1,2,…,m

(15)

式中,φ(S1,S2,S3)为目标函数;S1,S2,S3分别代表准则1～准则3。为确保权系数具有实际意义,故要求权系数σi必须为正数。

3 总体建模思路与分系统设计

3.1 总体建模思路步骤

利用非线性灰色网络神经算子(G-Verhulst-BP算子)在非线性残差修正中的优势,构建军费开支多目标组合预测模型,并采用EGA算法提高对组合预测目标函数的逼近速度和精度,给出具体的分系统设计与总体建模思路,完整过程如图1所示,大体分为4个步骤:

步骤1明确研究对象。采用计量经济学传统方法分析已知军费开支样本,检验其趋势性、异方差性、记忆性、自相关性等规律特点,针对性地进行数据平滑处理等准备工作,为进行特征描述与数学建模奠定基础。

步骤2基础模型设计与改进。按照步骤1中表现出的序列多样性特征,分别建立独立描述单一特征规律的多项式分布滞后(polynomial distribution lag,PDL)模型、自回归条件异方差(autoregressive conclitional heteroskedasticity,ARCH)模型和自回归积分滑动平均(autoregressive integrated moving average,ARIMA)模型等计量模型作为军费开支基础预测模型。利用残差检验对基础预测模型进行残差信息收集,引入非线性灰色神经网络算子(G-Verhulst-BP算子)进行残差修正,运用分系统一改进基础模型预测精度。分别构建非线性残差特征下的G-Verhulst-BP(PDL)模型、G-Verhulst-BP(ARCH)模型和G-Verhulst-BP(ARIMA)模型,构成模型组的基本形式为

(16)

式中,εt_PDL、εt_ARCH、εt_ARIMA为残差模型。

步骤3组合预测模型建立与优化。为建立G-Verhulst-BP计量组合预测模型,可以通过构建基于MSE、MAE、MAPE 3种准则的不同偏好映射,设计组合目标函数进行实现。利用分系统二来提高目标搜索效率与收敛速度,进一步提高军费开支预测精度。基本形式为

(17)

步骤4建模效果对比与评估。比较不同预测模型的预测精度,研究分系统设计对于提高模型预测精度的影响程度,并与EGA策略下的模型精度进行对比分析,研究收敛速度与精度的差异,说明引入非线性G-Verhulst-BP算子后的模型具有更强的优越性。

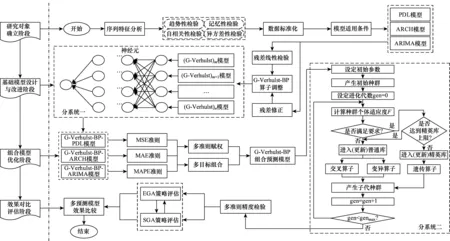
图1 军费开支多目标组合预测完整流程图Fig.1 Complete flow chart of military expenditure multi-objective combination forecasting

3.2 分系统一: 非线性灰色神经网络算子设计

分系统一的设计思想旨在构建一种S型非线性序列特征灰色神经网络算子,即G-Verhulst-BP算子。该算子吸收灰色理论与神经网络的优点,进行优势互补,具有自主学习能力强、计算量小、预测精度高、误差可控等突出特点。G-Verhulst-BP算子实现步骤如下:

步骤1程序初始化。导入原始数据序列η(0)=(η(0)(1),η(0)(2),…,η(0)(n)),设定建立G-Verhulst模型所需数据下限值m。

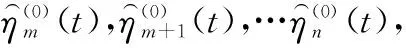
3.3 分系统二: EGA算法设计

分系统二主要设计思想是采用EGA[24-25]对目标收敛计算过程进行优化。该算法由标准遗传算法(standard genetic algorithm,SGA)与精英选择策略有机结合形成,能够有效克服SGA在使用过程中经常出现的个体早熟,防止掉进局部最优陷阱而导致的进化停滞现象,从而无法在全局范围内寻求最优的收敛结果。篇幅所限,关于分系统二的主要参数设定及程序实现步骤参考文献[26]。

4 实证研究

4.1 数据来源和研究样本

本文选取自“冷战”结束(以1989年柏林墙倒塌为标志)后美国27年间(1990-2016年)的军费开支作为研究样本,全部数据来源于瑞典斯德哥尔摩国际和平研究所官方年鉴。利用自然对数进行数据平滑处理,得到处理后原始时间序列样本27个。

4.2 实证分析

将军费开支样本数据分为拟合样本与预测样本两类,以美国军费开支1990-2013年的数据作为拟合样本,共24组,用于模型的初始构建。同时,以美国军费开支2014-2016年的数据作为预测样本,共3组,用于检验模型预测实际效果。考察序列的趋势性、记忆性、自相关性、异方差性等特征,分别建立基础模型——PDL、ARCH和ARIMA 3种计量经济模型进行军费开支预测。其中,ARCH模型的参数形式为GARCH(1,1),属于广义自回归条件异方差模型,适用于存在高阶残差自相关的情形。各基础模型参数特征与有效性检验结果如表1所示。

表1 基础模型及相关参数估计

结果显示,基本检验指标中赤池信息准则(Akaike information criterion,AIC)和施瓦茨准则(Schwarz criterion,SC)均处于可以接受的理想范围内,同时各基础模型均较好地通过L检验,说明模型参数正确,通过了显著性检验,即模型建立依据充分合理。对各基础模型残差进行线性假设检验,建立残差线性方程,检验结果具体如表2所示。

表2 残差方程与线性假设检验

表3 非线性残差G-Verhulst模型参数估计与误差修正

对24组军费开支数据进行样本分析(1990-2013年),给出了G-Verhulst-BP算子预测公式的基本参数。经过1 000次训练迭代后,模型残值拟合误差已经迅速缩小到到3.969×10-5,其修正后总误差分别为0.611、0.689和0.599,与相对应的基础模型预测误差相比,误差更小,结果更理想,说明模型修正后的预测精度得到有效提高。经训练后的残差估值与原值间拟合效果如图2和图3所示。

图2 非线性灰色神经网络算子训练效果Fig.2 Training effect of nonlinear gray neural network operator

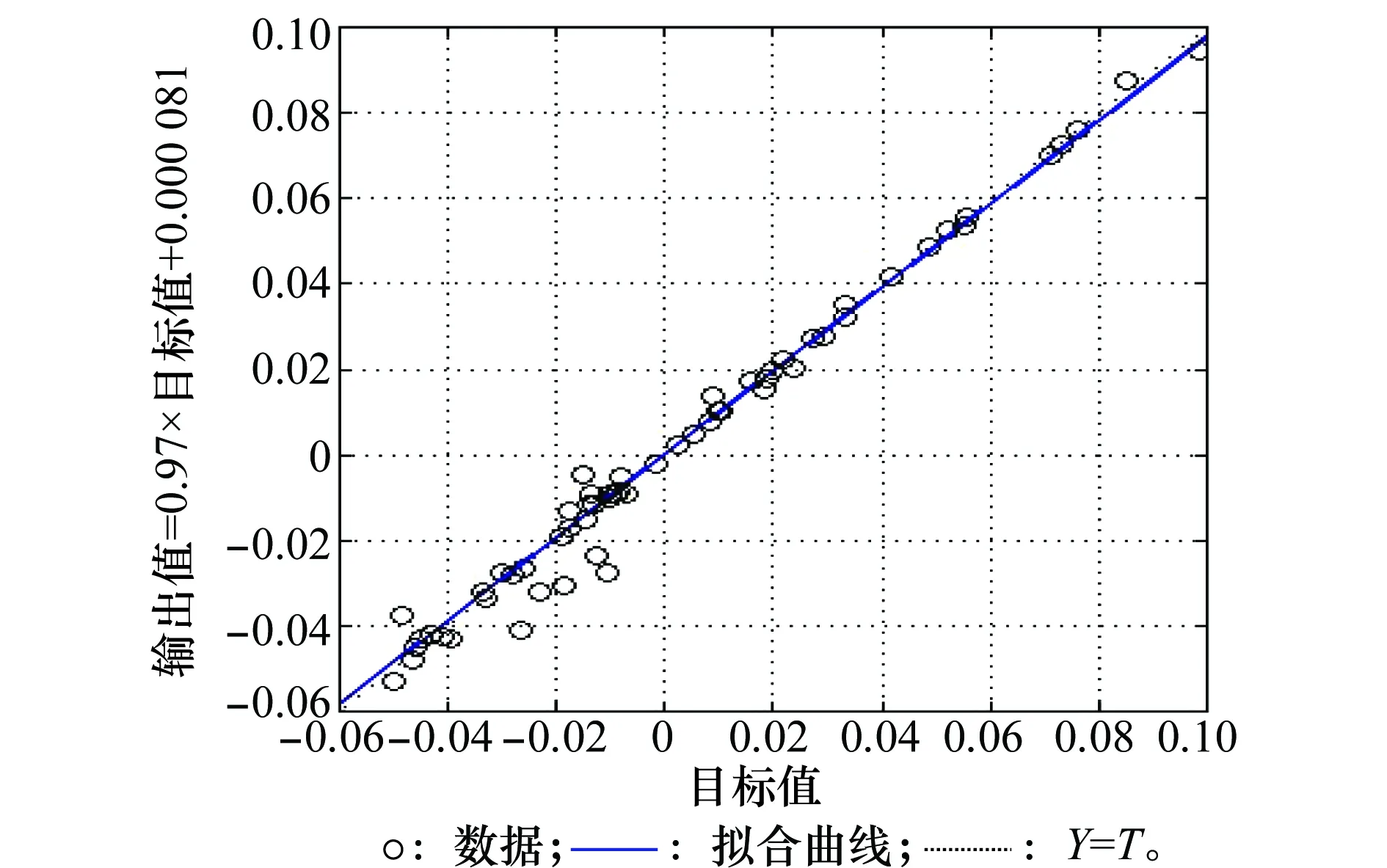
图3 非线性灰色神经网络算子残差拟合效果Fig.3 Residual fit effect of nonlinear gray neural network operator

综合考察G-Verhulst-BP(PDL)模型、G-Verhulst-BP(ARCH)模型和G-Verhulst-BP(ARIMA)模型,选取1990～2013年数据作为训练样本,构建G-Verhulst-BP计量组合预测模型,并利用EGA算法来优化模型计算结果。以滚动验证方式,分别将2014-2016年数据作为测试样本,检验最终模型预测效果。EGA算法的主要参数设定如下:种群规模Q=100,精英库种群规模Q*=10,种群进化代数阈值genmax=200,遗传概率pr=0.99,交叉概率pc=0.8,变异概率pn=0.2,适应度函数值偏差阈值为1×10-100;EGA算法运行环境如下:软件Matlab R2014a,操作系统Windows7,Intel(R) Core CPU P8700,主频2.53 GHz,内存2.99 G。结合上述设定,当目标函数为φ1=S1时,计算可以得到最佳个体值依次为0.303、0.159和0.538,最佳适应度值1.310×10-3。计算过程中最佳适应度迭代及个体距离散点分布情况等如图4～图6所示。

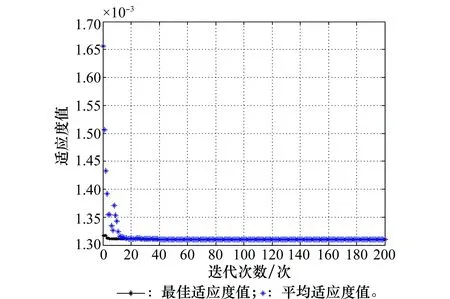
图4 EGA收敛散点图Fig.4 EGA convergence scatter plot

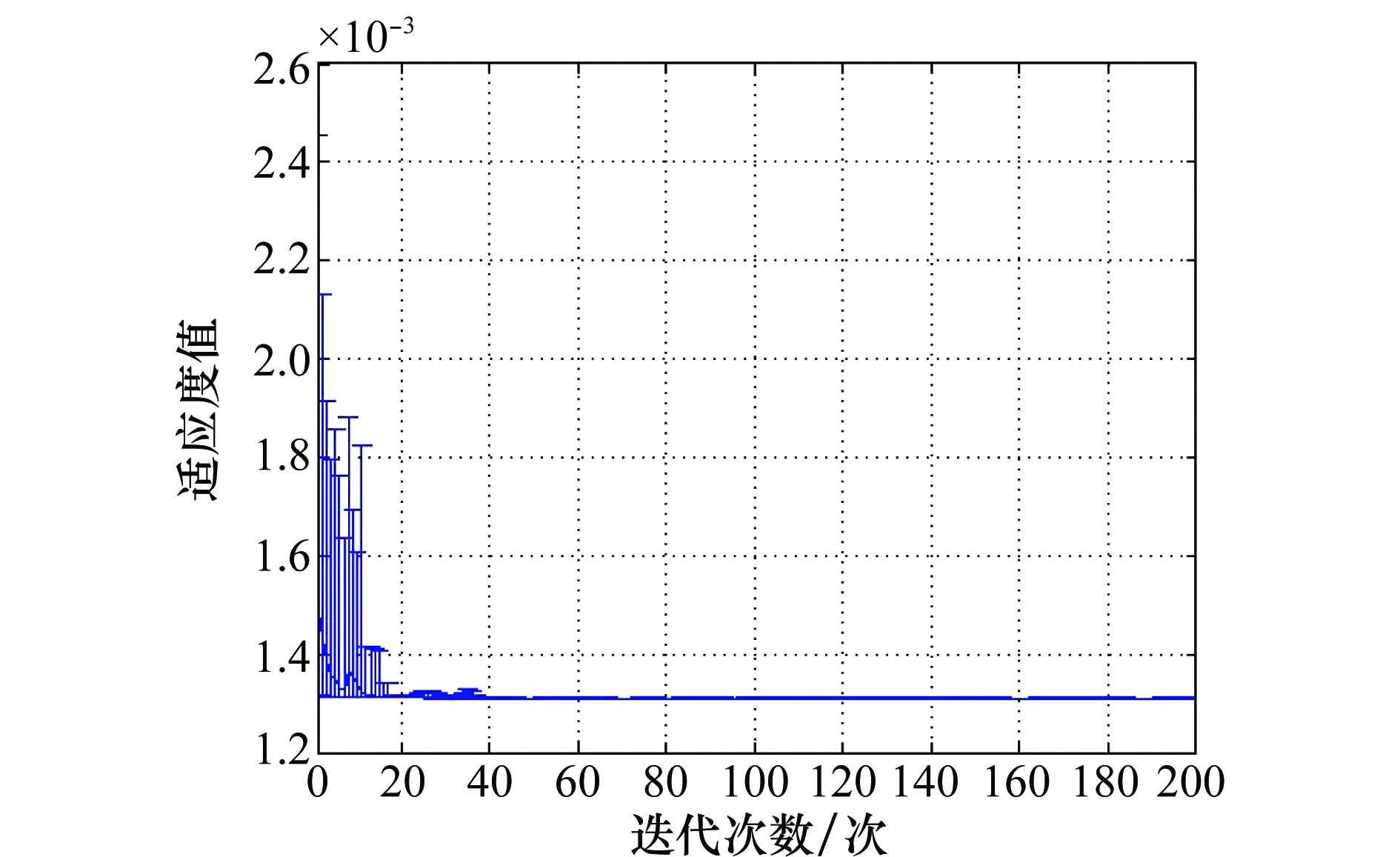
图5 同代最佳个体与最差个体适应度值比较Fig.5 Comparison of fitness values of the best and the worst individual in the same generation

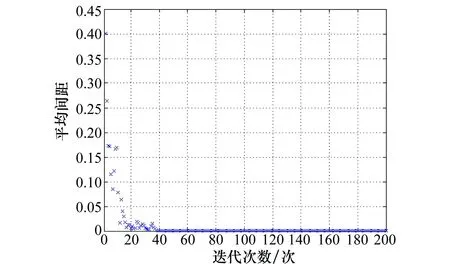
图6 种群个体平均间距散点图Fig.6 Scatter plot of average spacing of population

可以发现,种群最佳适应度值随着进化代数增加而迅速收敛,种群个体间距不断缩小,说明种群整体基因得到有效改善。大约经过20代后收敛效果已非常明显,40代后得到稳定的满意结果,算法整体运行时间较短,拟合结果较为精确。同理按照φ2=S2,φ3=S3,φ4=S1+S2+S3等目标函数进

行权重分配,得到表4中关于多目标组合预测NP完全问题的一组Pareto最优解。此时,不同目标函数下的各评价准则下的误差值均较小,各权重值相对稳定,说明G-Verhulst-BP计量组合预测模型已经满足预期要求,模型拟合效果优良,具有良好的稳定性。

4.3 算法分析评估

图7和图8显示,传统SGA算法在进化至160代左右才显著收敛于最优值,收敛速度仅为EGA算法的1/4。SGA算法的均方误差值达到1.437×10-3,大于EGA算法的均方误差,较EGA算法收敛速度稍慢,精确度较差。这说明相比而言,EGA算法综合性能更为优越。选择综合评价效果最好的G-Verhulst-BP计量组合预测模型形式④,比较各预测模型的预测效果。为便于语言叙述,令符号Ⅰ-Ⅶ依次分别代表PDL模型、ARCH模型、ARIMA模型、G-Verhulst-BP(PDL)模型、G-Verhulst-BP(ARCH)模型、G-Verhulst-BP(ARIMA)模型和EGA算法改进的非线性G-Verhulst-BP计量组合预测模型。预测样本为美国2014-2016年军费开支(对数化形式数据组),预测结果如表5所示。

表4 多准则目标决策下的Pareto最优解

图7 SGA算法收敛散点图Fig.7 SGA convergence scatter plot

图8 SGA算法同代个体适应度值比较Fig.8 Comparison of fitness values in the same generation by SGA

年份实际数值Ⅰ估值误差/%Ⅱ估值误差/%Ⅲ估值误差/%Ⅳ估值误差/%Ⅴ估值误差/%Ⅵ估值误差/%Ⅶ估值误差/%20148.7168.611-1.218.626-1.048.615-1.178.655-0.708.7570.468.669-0.548.678-0.4320158.6938.571-1.428.589-1.218.600-1.088.609-0.978.7540.698.7250.368.690-0.0320168.7188.567-1.768.580-1.608.580-1.608.701-0.198.8651.658.8361.338.7940.86

由表5知,模型Ⅶ的综合预测误差最小,因而该模型预测效果最佳。同时,模型Ⅳ、模型Ⅴ、模型Ⅵ考虑残差影响,利用非线性灰色神经网络算子进行残差修正,故预测效果优于基础模型Ⅰ～模型Ⅲ,符合残差修正理论预期。说明经过分系统一(非线性灰色神经网络算子)和分系统二(EGA)的二轮修正,能够有效提高军费开支模型预测效果。

5 结 论

本文从军费开支时序特征分析入手,利用MSE、MAE、MAPE等准则来研究多目标组合下的军费开支预测问题。为提高预测模型精度,引入G-Verhulst-BP算子和EGA算法进行模型精度改进。采用美国军费开支进行实证检验,对比不同模型拟合与预测结果,有以下结论:

(1) 3种G-Verhulst-BP算子预测模型(即G-Verhulst-BP(PDL)模型、G-Verhulst-BP(ARCH)模型、G-Verhulst-BP(ARIMA)模型)的修正后拟合误差均小于基础模型,总误差减少幅度依次为0.154、0.215、0.067,说明非线性灰色神经网络算子能够有效提高模型精度。

(2) EGA算法较SGA算法收敛精度更高(分别为1.310×10-3和1.437×10-3),收敛时间更短(分别为40代和160代),说明EGA算法在优化搜索过程中实际使用效果更好。

(3) 综合G-Verhulst-BP算子和EGA算法优点,本文构建的基于EGA算法改进的非线性G-Verhulst-BP计量组合预测模型2014-2016年预测平均误差为0.44%,小于其他预测模型,说明预测精度更高,预测建模效果更好。

参考文献：

[1] 姜鲁鸣. 加强军费战略管理的思考[J]. 国防大学学报, 2013, 292(9): 40-43.

JIANG L M. Thoughts on strengthening military insurance strategic management[J]. Journal of National Defence University, 2013, 292(9):40-43.

[2] 张侃,刘宝平,黄栋,等.我国国防支出与经济增长、居民消费的关系实证研究[J]. 海军工程大学学报, 2016,28(5): 69-74.

ZHANG K, LIU B P, HUANG D, et al. An empirical study on relationship among defense expenditure, economic growth and private consumption[J]. Journal of Naval University of Engineering, 2016, 28(5): 69-74.

[3] 张世英, 樊智. 协整理论与波动模型[M]. 北京: 清华大学出版社, 2007.

ZHANG S Y, FAN Z. Cointegration theory and volatility models[M]. Beijing: Tsinghua University Press, 2007.

[4] 张玲, 刘波. 基于残差统计的时间序列加性离群点检测算法研究[J]. 电子技术应用, 2015, 41(9): 85-87.

ZHANG L, LIU B. Residuals statistics-based additive outlier detection algorithm for time series[J]. Application of Electronic Technique, 2015, 41(9): 85-87.

[5] WANG X M, YAO Z M, DMITRI L. Residual-based estimation of peer and link lifetimes in P2P networks[J]. Transactions on Networking, 2009, 17(3): 726-739.

[6] LIN C H, SHEN D Y. Secret: a selective error correction framework for refresh energy reduction in drams[J]. ACM Trans.on Architecture and Code Optimization,2015,12(2):19-24.

[7] BERTOZZI D, OLIVO P, ZAMBELLI C. Flares: an aging aware algorithm to autonomously adapt the error correction capability in NAND flash memories[J]. ACM Trans.on Architecture and Code Optimization, 2014, 11(3): 26-50.

[8] BATE J M, GRANGER C W J. Combination of forecasts[J]. Operations Research Quarterly, 1969, 20(4): 451-468.

[9] CHRISTIANE L. Combinations of time series forecasts: when and why are they beneficial[D]. Bournemouth: Bournemouth University, 2010.

[10] LI H A, KANG B S, ZHANG J. Combined forecasting model of cloud computing resources based on improved encompassing tests and IOWA operator[J]. Journal of Computational Information Systems, 2013, 9(7): 2631-2640.

[11] HARVEY N, HARRIES C. Effects of judges’ forecasting on their later combination of forecasts for the same outcomes[J]. International Journal of Forecasting, 2004, 20(3): 391-409.

[12] 高放. 组合预测研究及其在交通流量预测中的应用[D]. 济南: 山东科技大学, 2008.

GAO F. Study of combination forecast and application in traffic flow forecast[D]. Jinan: Shandong University of Science and Technology, 2008.

[13] 丁咏梅. 我国股票价格的组合预测[D]. 武汉: 华中科技大学, 2005.

DING Y M. The application and some discussion of combination forecast about chinese stock market[J]. Wuhan: Huazhong University of Science and Technology, 2005.

[14] 何满喜. 组合预测方法在旅游经济分析预测中的应用[J]. 数学的实践与认识, 2010, 40(3): 1-6.

HE M X. The application of combination forecast method in analysis and forecasting of tourism economy[J]. Mathematics in Practice and Theory, 2010, 40(3): 1-6.

[15] 邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002.

DENG J L. The basis of grey theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002.

[16] 赵玲,唐敏康.基于残差修正GM(1,1)模型的火灾事故预测[J].数学的实践与认识,2012, 42(18): 82-87.

ZHAO L, TANG M K. Prediction of fire accidents based on GM(1,1) model with residual error correction[J]. Mathematics in Practice and Theory, 2012, 42(18): 82-87.

[17] YAO T X, FORREST J, GONG Z W. Generalized discrete GM(1,1) model[J]. Grey Systems: Theory and Application, 2012, 2(1): 4-12.

[18] 仇伟杰, 刘思峰. GM(1,N)模型的离散化结构解[J]. 系统工程与电子技术, 2006, 28(11): 1679-1699.

QIU W J, LIU S F. Dispersed structure solve of model GM(1,N)[J]. Systems Engineering and Electronics, 2006, 28(11): 1679-1699.

[19] TIEN T L. The indirect measurement of tensile strength of material by the grey prediction model GMC(1,N)[J]. Measurement Science Technology, 2005(16): 1322-1328.

[20] TIEN T L. A research on the grey prediction model GM(1,N)[J].Applied Mathematics and Computation,2012,218(9):4903-4918.

[21] 徐黎明,王清,陈剑平,等.基于BP神经网络的泥石流平均流速预测[J].吉林大学学报(地球科学版),2013,43(1):186-191.

XU L M, WANG Q, CHEN J P, et al. Forcast for average velocity of debris flow based on BP neural network[J]. Journal of Jilin University (Earth Science Edition),2013,43(1):186-191.

[22] 杨武,张春燕,马超.基于GA-BP神经网络的镁合金微弧氧化膜层厚度预测[J].兵器材料科学与工程,2017,40(1):88-92.

YANG W, ZHANG C Y, MA C. Thickness prediction of micro-arc oxidation coating on magnesium alloy based on GA-BP neural network[J]. Ordnance material science and engineering, 2017, 40(1): 88-92.

[23] 孙志强,葛哲学. 神经网络理论与Matlab 7实现[M]. 北京: 电子工业出版社, 2005.

SUN Z Q, GE Z X. Neural network theory and Matlab 7 application[M]. Beijing: Electronics Industry Press, 2005.

[24] KIM J L. Permutation based elitist genetic algorithm using serial scheme for large-sized resource-constrained project scheduling[C]∥Proc.of the Winter Simulation Conference, 2007: 2112-2118.

[25] 巴海涛, 史超. 基于精英保留遗传算法的飞行器航路规划[J]. 指挥控制与仿真, 2010, 32(4): 42-46.

BA H T, SHI C. A route planning algorithm for aircraft based on elitist genetic algorithm[J]. Command Control & Simulation, 2010, 32(4): 42-46.

[26] 张侃, 刘宝平, 黄栋. 基于EGA算法的小样本非线性残差灰色Verhulst计量组合预测模型[J]. 系统工程理论与实践, 2017,10(10): 2630-2639.

ZHANG K, LIU B P, HUANG D. Study on nonlinear residual grey Verhulst metering combination forecasting model of small sample based on EGA algorithm[J]. Systems Engineering—Theory & Practice, 2017,10(10): 2630-2639.