FDA-MIMO雷达主瓣距离欺骗式干扰抑制方法

兰 岚, 廖桂生, 许京伟, 张玉洪

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西安电子科技大学电子工程学院, 陕西 西安 710071)

0 引 言

随着信息技术的不断发展,雷达干扰和抗干扰之间的斗争日趋激烈和复杂[1-2]。其中,欺骗式干扰通过辐射类似于目标回波的电磁波,诱使雷达系统把虚假目标当成真实目标来处理,影响其对真实目标的参数估计与跟踪,对雷达的战场生存能力造成巨大威胁。假目标信号作为一种重要的干扰手段,通常由干扰机将截获的雷达信号存储后进行延迟转发并通过距离欺骗、多普勒调制等手段产生。随着数字射频存储器(digital radio-frequency memory,DRFM)技术的发展,目标回波信号能被精确复制出来,干扰样式也更加复杂[3-4]。目前针对有源欺骗式干扰的主要对抗措施是利用干扰信号和有用信号在时域[5]、频域[6]、空域和极化域[7]等方面的差异进行区分,采取信号处理达到从干扰背景中提取有用信息的目的。由于干扰机截获、储存和重构雷达发射信号需要一定的时间,即干扰脉冲至少要滞后雷达发射脉冲一个脉冲重复周期,可结合波形分集技术,利用有用信号和干扰信号波形参数的差异进行对抗[8]。通过波形捷变[9-10]的方法可提高雷达系统的抗干扰能力,但是会导致高的距离旁瓣,限制了雷达输出信干比的提高和对干扰的抑制性能。 实际上,传统雷达对抗主瓣欺骗式干扰有一定难度,因此,在新体制雷达下挖掘目标和干扰的多参数信息成为抗主瓣欺骗式干扰的一种重要途径。

频率分集阵列(frequency diverse array, FDA)的概念自2006年提出以来[11],得到了雷达领域国内外学者的广泛关注,主要包括:①发射方向图特性分析[12-14];②方向图解耦和技术[15-17];③FDA系统设计[18-20];④结合多输入多输出(multiple input and multiple output,MIMO)波形,基于FDA-MIMO雷达[21-23]、FDA双基雷达[24]、FDA认知雷达等[25-26];⑤基于FDA的一些应用如目标参数估计[27-28]、无模糊成像[29]、杂波抑制[30]等。FDA通过在阵元之间引入频率步进量,在发射端等效增加了随距离而变化的权值,增加了额外的距离维可控自由度,因此可以利用真实目标与主瓣欺骗式干扰的距离信息差异来进行辨别。文献[31]研究了FDA-MIMO雷达自适应距离角度二维波束形成方法,并提出了一种基于直接数据域的稳健距离-角度二维波束形成方法,可用来抑制欺骗式干扰。然而该方法假定由同一假目标产生器(false target generation, FTG)产生的假目标在发射-接收维具有相同的导向矢量,这一假设条件仅是众多实际情况中的特例。

本文在FDA-MIMO雷达体制下提出了一种抑制主瓣距离欺骗式干扰的方法。由于FTG对截获的雷达信号进行延迟转发形成具有不同的距离频率的假目标,故真、假目标存在时延(或距离)差异。当存在距离模糊时,并且假设已具备真实目标位置信息的先验知识。在上述前提条件下,真、假目标具有不同的主值距离以及距离模糊次数。首先利用真实目标的主值距离对发射频率进行初相补偿,其次在联合发射-接收二维频率域上对真、假目标进行区分,最后通过距离-角度二维自适应匹配滤波来抑制距离维失配的主瓣距离欺骗式干扰。

1 FDA-MIMO雷达主瓣距离欺骗式干扰模型

不失一般性,考虑由M个发射阵元,N个接收阵元组成的等距线阵,其发射频率以Δf线性递增。在FDA-MIMO系统中,第m个阵元发射频率为

fm=f0+(m-1)Δf,m=1,2,…,M

(1)

式中,f0为参考阵元(第一个阵元)频率。第m个阵元发射信号为

(2)

假设远场某位置(R0,θ0)处存在单点目标源,则第n个阵元接收的来该目标的反射信号可表示为

(3)

式中,β为点目标复散射系数;双程时延

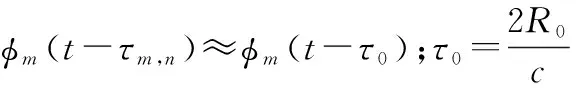
(4)

xS=[y11,y12,…,y1N,y21,…,yMN]T=

ξSb(θ0)⊗a(R0,θ0)

(5)

式中,⊗表示Kronecker积;a(R0,θ0)∈CM×1和b(θ0)∈CN×1分别为发射和接收导向矢量,其表达形式分别为

(6)

(7)

式中,⊙表示Hadamard积,可见目标距离维信息包含在发射导向矢量里。

敌方FTG将截获的雷达信号进行延迟转发形成假目标,迷惑我方雷达接收机。假设FTG位于(Rj,θj)处。则第n个阵元接收到的被FTG转发的信号可以表达为

(8)

式中,L为FTG产生的假目标数;

为第n个接收阵元与FTG的双程时延;τl为对于第l个假目标的调制时间。FTG会在下一个雷达脉冲到来之前通过延迟τl来产生具有负的距离偏移的假目标,即假目标所在的距离门由FTG中存储的时间延迟决定。对于主瓣欺骗式干扰有θ0=θj。此外,由同一FTG产生的假目标信号可近似认为相干,即对于所有接收阵元来说,βj都相同。第n个阵元接收到的第l个假目标信号经匹配滤波后,得到

(9)

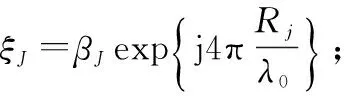
xl=[Jl,11,Jl,12,…,Jl,1N,Jl,21,…,Jl,MN]T=

ξJbJ(θj)⊗aJ(Rl,θj)

(10)

由此可得,FDA-MIMO雷达的接收信号可表示为

⊗a(R0,θ0)+

(11)

式中,xS为真实目标信号分量;xl为假目标信号分量;n表示噪声分量。

2 基于时延(距离)差异的主瓣距离欺骗式干扰抑制

FTG将截获的雷达信号延迟一个或多个脉冲周期,再进行转发形成假目标,从而干扰了雷达对真实目标的识别和跟踪。距离欺骗式干扰的效果表现为,产生的若干假目标具有正的或负的距离偏移,可出现在目标的前方或后方,且假目标所在的距离门由FTG中的延时决定。

本文假设真实目标的距离和角度信息已知(例如,在搜索阶段完成目标信息的粗估计),这是鉴别真、假目标的重要前提。由式(6)和式(7)可导出目标相应的发射空间频率fT和接收空间频率fR：

(12a)

(12b)

同理,由FTG产生的第l个假目标对应的发射和接收空间频率分别表示为

(13a)

(13b)

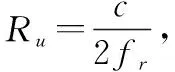
R0=r0+(p-1)Ru

(14)

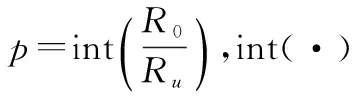
Rl=rl+(pl-1)Ru

(15)

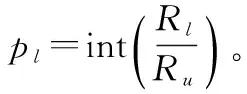
(16)

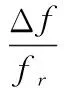
由式(14)和式(15)可知,根据主值距离和模糊次数的差异可鉴别真、假目标。由于主值距离可以直接估计得到,对于不同主值距离的真、假目标较好区分,而对于处于同一距离门的真实目标与假目标(主值距离相同),则额外需要模糊次数作为判定条件,因此本文假设距离模糊这一前提条件很关键。图1模拟了距离欺骗式干扰的产生过程。假设两个FTG被放置在远离战场的敌后用来保护目标,FTG截获后雷达信号后,通过内部时间调制,延迟若干脉冲后转发产生若干假目标。其中假目标1和假目标2由FTG1产生,假目标3由FTG2产生。在一个无模糊区间内,由于假目标1和假目标3与真实目标的主值距离不同,因此容易区分,而对于恰好与真实目标位于同一个距离门内的假目标2,根据其与真实目标模糊次数的差异,从而可以区分。基于上述分析,假设雷达接收到的回波信号的主值距离为r′,计算的模糊次数为p′,可以构造下列三元假设问题来判断真、假目标:

(17)

式中,H0假设表示收到的回波信号为真实目标;H1和H2假设表示接收到的回波信号为假目标。

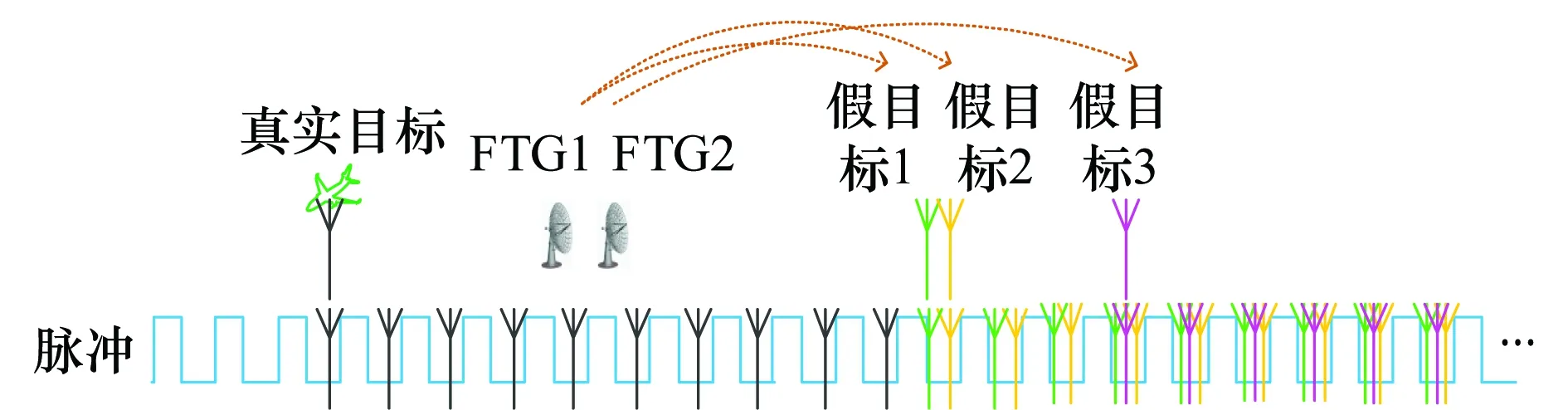
图1 距离欺骗式干扰产生过程Fig.1 Generation procedure of range deceptive jamming

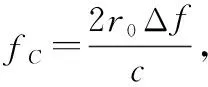
h=[1,ej2πfC,…,ej2π(M-1)fC]T

(18)

则在联合发射-接收空间频率域补偿矢量可表示为

g=1N×1⊗h=[1,1,…,1]T⊗[1,ej2πfC,…,ej2π(M-1)fC]T

(19)

式中,1N×1表示全1的列矢量。利用频率补偿量分别对真实目标和每一个假目标的发射空间频率进行补偿,则补偿后的真实目标与假目标的发射空间频率可以表示为

(20a)

(20b)

式中,rΔ表示第l个假目标补偿后的剩余主值距离。由此可见,经过补偿后真、假目标在发射空间频率上存在差异,因此可利用这一特性在联合发射-接收频域上实现真、假目标的鉴别,且真、假目标的发射空间频率差可以具体表示为

(21)

为了在发射空间频域上有效实现真、假目标的鉴别,需要较大的Δf来保证ΔfTx-comp<1,此外,为了精确估计距离模糊数,需要对频率步进量Δf进行设计。文献[32]给出了频率步进量的最优选择,表示如下：

(22)

式中,B为发射信号带宽；Na为最大模糊次数,且频率步进量越大,距离估计精度越高[32]。

补偿后的接收数据可进一步等效表示为

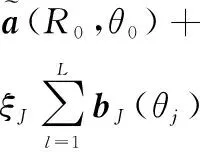
(23)

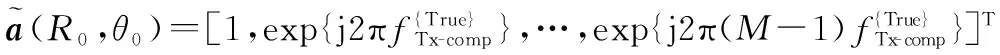
通过以下优化问题可以设计距离-角度自适应匹配滤波器

(24)

式中,Rj+n表示干扰加噪声协方差矩阵;u(R0,θ0)=b(θ0)⊗a(R0,θ0)表示FDA-MIMO雷达虚拟导向矢量;wopt为根据拉格朗日乘子法计算的自适应最优权[33]。整个算法的计算复杂度为O((MN)3)。

将补偿后的接收数据通过该距离-角度自适应匹配滤波器,得到输出为

(25)

由于假目标在距离维上的不匹配,因此在通过距离-角度二维自适应匹配滤波后会被抑制,从而解决主瓣距离欺骗式干扰抑制问题。图2给出了基于时延(距离)差异的主瓣距离欺骗式干扰抑制流程图。

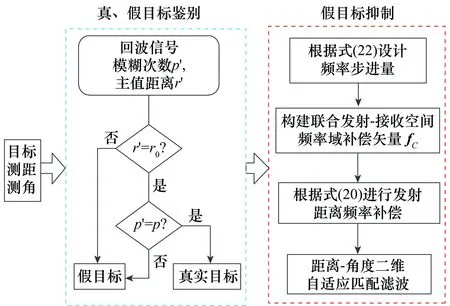
图2 基于时延(距离)差异的主瓣距离欺骗式干扰抑制流程图Fig.2 Process of main-beam range deceptive jamming suppression based on the time delay or range difference

3 仿真实验

本节通过仿真数据来验证所提基于时延(距离)差异的方法对主瓣距离欺骗式干扰抑制的有效性。表1给出了相应的仿真参数。假设Na=4,Δf=1 871 250 Hz。由此,利用式(16)可以计算得u=374,q=0.25。假设FTG位于主瓣,而FTG2位于旁瓣。距离门数为200,由FTG1产生的假目标1和假目标2分别位于第35个距离门和第134个距离门上,由FTG2产生的假目标3位于第167个距离门,真实目标与假目标2共同位于第134个距离门。

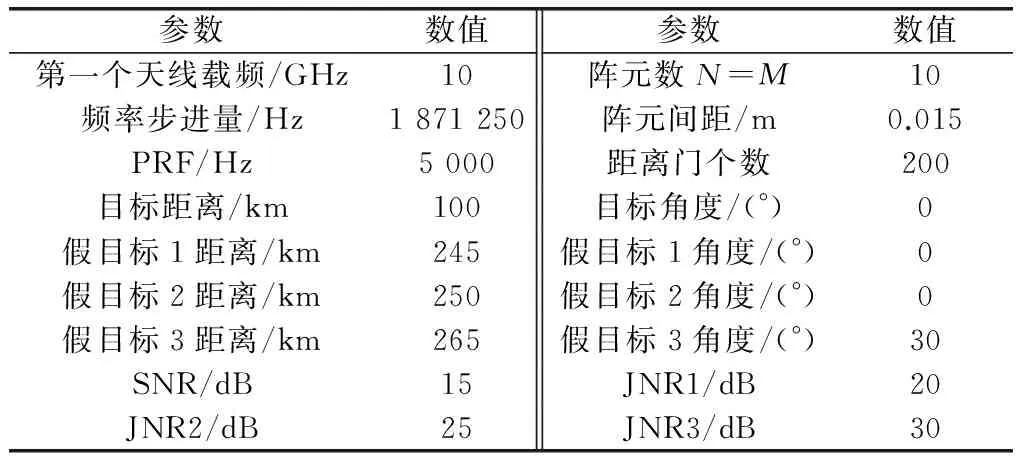
表1 FDA-MIMO雷达系统仿真参数

图3给出了真、假目标分布功率谱图及方向图。如图3(a)所示,在传统的MIMO雷达中,由于真实目标、假目标1和假目标2具有相同的发射和接收频率,因此在发射-接收二维频域呈对角线分布。而在图3(b)中,由于FDA-MIMO发射导向矢量具有距离-距离二维依赖性,因此目标在发射-接收二维域上任意分布。真、假目标具有不同的发射空间频率,经过发射频率补偿后,可以在联合发射-接收频域可以被区分出来。值得注意的是,对于处在同一距离门内的真实目标和假目标2,由于它们具有不同的模糊次数,进而发射空间频率存在差异,因此可以在发射-接收二维频域上区别开来。图3(c)为对应的FDA-MIMO雷达距离-角度二维域自适应波束形成结果。由于仅真实目标信号的角度、距离信息与约束相吻合,因此经过自适应波束形成器,获得最大输出,而假目标由于距离维信息的不匹配被抑制。图3(d)对比了传统单输入单输出(single input single output,SISO)雷达、MIMO雷达以及FDA-MIMO雷达的方向图剖面。SISO雷达不具备抗干扰的能力,而在MIMO雷达中由于主瓣干扰的存在会导致目标信号相消,引起自适应方向图畸变。

图3 真、假目标分布功率谱图及方向图Fig.3 Capon spectrum distribution and beampatterns of the true and false targets

图4给出了距离-角度二维匹配滤波输出。如图4(a)所示,对于FDA-MIMO雷达,通过距离-角度二维自适应匹配滤波,真实目标获得输出功率最大,而假目标信号由于距离维信息的失配而被抑制。图4(b)对比了传统SISO雷达,MIMO雷达和FDA-MIMO雷达在0°的输出功率剖面。对于SISO雷达,由于同时缺乏角度和距离维的自由度,目标检测的虚警率较高,在所有假目标处仍有较高的输出功率。对于MIMO雷达,由于没有距离维自由度,仅靠角度维自由度无法抑制距离欺骗式干扰信号,只能抑制角度失配的假目标3。而FDA-MIMO雷达同时具有角度和距离维的自由度,由于假目标距离维信息不匹配,因此经过距离-角度二维自适应匹配滤波,所有假目标均能被有效地抑制,从而解决了主瓣距离欺骗式干扰抑制这一问题。

图5对比了SISO、传统MIMO雷达以及FDA-MIMO雷达的输出信干噪比(signal-to-interference plus noise ratio,SINR)与输入信噪比(signal-to-noise ratio,SNR)的变化曲线。在FDA-MIMO雷达中,经过距离-角度二维自适应匹配滤波,可实现对距离失配假目标信号的抑制,因此在输出端获得较高的SINR。在MIMO雷达中,由于欺骗式干扰位于天线主瓣,因此会造成目标相消,输出SINR性能较差。此外,SISO不具备抑制干扰的能力,因此其输出SINR最低。

4 结 论

本文运用FDA-MIMO雷达体制,提出一种基于时延(距离)差异的主瓣距离欺骗式干扰抑制方法。考虑FTG将截获的雷达信号延迟一个或多个脉冲周期转发形成多个假目标。在距离模糊存在的条件下,真、假目标具有不同的模糊次数与主值距离。因此,本文首先利用真实目标的主值距离构造补偿矢量,对发射空间频率进行补偿,随后在在联合发射-接收二维频率域上根据真、假目标距离频率的差异对它们进行分辨。最后将接收的信号通过距离-角度二维自适应匹配滤波,假目标由于距离维的不匹配被抑制,从而有效地解决了主瓣距离欺骗式干扰抑制的问题。

参考文献：

[1] FARINA A. Electronic counter measure[M]. New York: McGraw Hill, 2008.

[2] 格雷厄姆. 通信、雷达与电子战[M]. 汪连栋译. 北京: 国防工业出版社, 2013.

ADRIAN G. Commutations, radar and electronic warfare[M]. WANG L D,trans. Beijing: National Defense Industry Press, 2013.

[3] OLIVIER K, CILLIERS J E, PLESSIS D M.Design and performance of wideband DRFM for radar test and evaluation[J]. Electronic Letter, 2011, 47 (14): 824-825.

[4] SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Trans.on Aerospace & Electronic Systems, 2006, 42(1):191-205.

[5] 张帅. 分布式雷达抗干扰与目标检测方法研究[D]. 成都: 电子科技大学, 2017.

ZHANG S. Research of distributed radar technology against jamming and target detection[D]. Chengdu: University of Electronic Science and Technology of China, 2017.

[6] 李永平. SMSP 和 C&I 距离假目标欺骗干扰识别和抑制方法研究[D]. 成都: 电子科技大学, 2012

LI Y P. Research of SASP and C&I range false target deceptive jammings identification and suppression[D]. Chengdu: University of Electronic Science and Technology of China, 2012.

[7] 施龙飞,任博,马佳智,等. 雷达极化抗干扰技术进展[J]. 现代雷达,2016, 38(4):1-7.

SHI L F, REN B, MA J Z, et al. Recent developments of radar anti-interference techniques with polarimetry[J]. Modern Radar, 2016, 38(4):1-7.

[8] 吴健. 基于波形分集的雷达抗有源欺骗干扰技术研究[D]. 成都:电子科技大学,2015.

WU J. Research of the technology against radar active deception jamming based on waveform diversity[D]. Chengdu: University of Electronic Science and Technology of China, 2015.

[9] ZHANG J, ZHU D, ZHANG G. New anti-velocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Trans.on Aerospace & Electronic Systems,2013,49(2):1290-1300.

[10] AHMED A, ZHAO Y, MOHAMMED R, et al. An improved radar ECCM method based on orthogonal pulse block and parallel matching filter[J]. Journal of Communications, 2015,10(8):610-614.

[11] ANTONIK P, WICKS M C, GRIFFITHS HD, et al. Range dependent beamforming[C]∥Proc.of the International Waveform Diversity and Design Conference, 2006: 22-27.

[12] WANG W Q. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar & Navigation, 2016, 10(6):1001-1012.

[13] XU Y H, SHI X W, XU J W, et al. Range-angle-dependent beamforming of pulsed frequency diverse array[J].IEEE Trans.on Antennas and Propagation, 2015, 63(7): 3262-3267.

[14] SECMEN M, DEMIR S, HIZAL A, et al. Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]∥Proc.of the IEEE Radar Conference, 2007: 427-430.

[15] KHAN W, QURESHI I M, BASIT A, et al. Range-bins-based MIMO frequency diverse array radar with logarithmic frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 885-888.

[16] LIU Y, RUAN H, WANG L, et al. The random frequency diverse array: a new antenna structure for uncoupled direction-range indication in active sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 295-308.

[17] GAO K, WANG W Q, CAI J, et al. Decoupled frequency diverse array range-angle-dependent beampattern synthesis using non-linearly increasing frequency offsets[J]. IET Microwaves Antennas & Propagation, 2016, 10(8):880-884.

[18] JONES A M,RIGLING R. Planar frequency diverse array radar receiver architecture[C]∥Proc.of the International Radar Conference, 2012: 145-150.

[19] JONES A M, RIGLING B D. Frequency diverse array radar receiver architectures[C]∥Proc.of the International Waveform Diversity & Design Conference,2012:211-217.

[20] XU J W, LIAO G S, ZHU S Q. Receive beamforming of frequency diverse array radar systems[C]∥Proc.of the XXXI URSI General Assembly and Scientific Symposium, 2014: 1-4.

[21] WANG W Q,SHAO H Z. A flexible phased-MIMO array antenna with transmit beamforming[J]. International Journal of Antennas Propagation, 2012(2012):473-475.

[22] SAMMARTINO P F, BAKER C J, GRIFFITHS H D. Frequency diverse MIMOtechniques for radar[J]. IEEE Trans.on Aerospace & Electronic Systems, 2013,49(1):201-222.

[23] GAO K, WANG W Q, CAI J. Frequency diverse array and MIMO hybrid radar transmitter design via Cramér-Rao lower bound minimization[J]. IET Radar, Sonar & Navigation, 2016, 10(9): 1660-1670.

[24] SAMMARTINO P F,BAKER C J. Developments in the frequency diverse bistatic system[C]∥Proc.of the IEEE Radar Conference, 2009: 1-5.

[25] BASIT A, QUREAHI I M, KHAN W, et al. Cognitive frequency offset calculation for frequency diverse array radar[C]∥Proc.of the 12th International Bhurban Conference on Applied Sciences and Technology, 2015: 641-645.

[26] WANG W Q. Cognitive frequency diverse array radar with situational awareness[J].IET Radar,Sonar & Navigation,2016,10(2): 359-369.

[27] WANG W Q. Range-angle dependent transmit beampattern synthesis for linear frequency diverse arrays[J]. IEEE Trans.on Antenna and Propagation, 2013, 61(8): 4073-4081.

[28] XU J W, LIAO G S, ZHANG Y H, et al. An adaptive range-angle-Doppler processing approach for FDA-MIMO radar using three-dimensional localization[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11 (2): 309-320.

[29] WANG C H, XU J W, LIAO G S, et al. A range ambiguity resolution approach for high-resolution and wide-swath SAR imaging using frequency diverse array[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2):336-346.

[30] XU J W, ZHU S Q, LIAO G S. Range ambiguous clutter suppression for airborne FDA-STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing,2015,9(8):1620-1631.

[31] XU J W, LIAO G S, ZHU S Q, et al. Deception jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015(113): 9-17.

[32] XU J W, LIAO G S, ZHU S Q, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Trans.on Signal Processing, 2015, 63(13):3396-3410.

[33] VAN TREE H L. Optimum array processing[M]. New York: Wiley, 2002.