基于2阶段优化的高速列车节能运行仿真研究

曹佳峰，刘斌

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

高速列车具有安全正点、舒适便捷和运输能力强等特点，并在交通中扮演越来越重要的角色[1]。高速列车运行速度和运行距离的增长伴随着巨大的能源消耗，通过高速铁路运营能耗的综合统计，整个高速铁路能耗的 80%以上均与列车牵引运行相关[2]。高速列车节能运行优化是在保证列车安全、正点的前提下，优化现有的列车速度运行曲线，实现能耗最小。针对高速列车节能运行优化问题，国内外学者进行了广泛深入研究。Milroy[3]指出，当列车运行在较为平缓的坡道或平道时，若运行距离较短且无临时限速，则列车优化运行可分为全力加速、惰行和全力制动3个方面。Chang等[4]建立了以能耗、正点和乘坐舒适度为目标的高速列车优化控制模型，运用遗传算法来优化惰行控制策略。Howlett[5−6]证明了一条优化运行曲线应该包含“加速、匀速、惰行、制动”4种序列，并且重新阐述了如何优化不同工况之间的切换。Sicre[7]基于遗传算法和列车动力仿真模型设计一种限速线路上列车运行模式，根据有效的速度调节来实现节能驾驶，并且通过司机的实际操纵证明其20%的节能效果。随着我国高铁迅速发展，越来越多学者从事高速列车节能运行优化研究。毛保华等[8−9]研究通用型列车运行计算系统，并运用启发式算法寻优实现节能运行。催恒斌等[10−11]针对国内既有高速列车制动利用率较低的特点，确定既有高速列车节能运行操纵策略，通过启发式算法离线求解各运行操纵策略转换点，并以京沪段为例进行试验和仿真分析。宋文婷等[12]引入组合优化技术，充分利用线路坡度，提出坡道加速度一次变更原则，并结合列车的操纵模式，最后获得能耗最小的速度运行曲线，指导高速列车下一站间的运行。以上研究成果丰富了高速列车节能运行理论和实际操纵策略，然而线路信息利用不够充分，对列车运行曲线的优化限于一次优化，并且以全局优化为主。为了将列车运行过程中所有条件结合起来获得更好的节能效果，本文提出包含坡道运行优化和全线惰行优化的2阶段优化方法，以高速列车牵引计算为基础，以运行能耗最小为优化目标，分别构建定时、精确停车约束下的节能模型。采用遗传算法求解寻优，得到优化后的速度运行曲线，达到节能运行目的。通过实例仿真对2阶段优化方法的有效性进行验证。

1 高速列车牵引计算分析

1.1 受力分析

依据《列车牵引计算规程》[13]中相关规定，可将列车视为一个单一的质点，忽略车辆之间的相互作用力。在单质点模型中，列车运行过程主要受到牵引力F，运行阻力W和制动力B的综合作用。列车牵引力是关于运行速度v的二次函数，可按照牵引特性曲线图取值。

列车运行阻力是阻碍列车运行且不受人力操纵的外力，包括基本阻力和附加阻力2部分。运行速度v是影响基本阻力的主要因素，一般公式为：

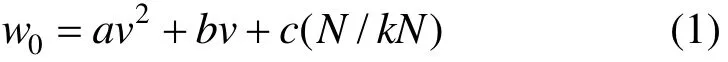
式中：a，b和c为常数，根据高速列车型号确定。附加阻力是由坡道或穿越隧道等线路条件形成的阻力，包括坡道附加阻力、曲线附加阻力和隧道附加阻力。分别表示为：

式中：i为线路的坡度，是坡道高度差与坡道水平距离的比值，以千分数(‰)表示；列车上坡时wi为正值，阻碍运行，列车下坡时wi为负值，推动运行；α为曲线中心角；Lr为曲线长度；Ls为隧道长度。

列车制动力是由制动装置引起的、与列车运行方向相反、阻碍列车运行的外力[14]。高速列车的制动属于再生制动，当列车处于制动工况时，车载再生设备把列车的动能转换为电能反馈到牵引电网，减少运行能耗。

1.2 运动学方程描述

在描述列车运动学方程时，将列车视为单质点来分析各种作用力。根据牛顿第二定律，列车的加速度与所受的合力成正比，其关系为：

式中：C为列车所受合力，N；M为列车总重，kg；a为列车的加速度，m/s2。

列车在运行过程中，牵引力和制动力不能同时存在，而运行阻力贯穿整个运行过程。列车所受的合力C取决于4种不同的运行工况，即牵引、匀速、惰行和制动，其中匀速工况是列车匀速运行状态，合力为0；牵引工况下，合力C=F−W；惰行工况下，合力C=−W；制动工况下，合力C=−B−W。因为列车牵引力F，基本阻力w0和制动力B都是运行速度v的函数，所以在确定列车所受合力后，列车运动学方程描述为：

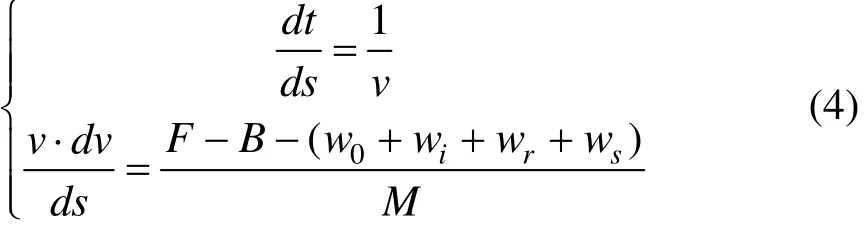
2 坡道运行优化

2.1 运行线路离散化

由于高速列车在其线路上有频繁的坡度变化，本文将线路按等坡道值离散化，把坡度值相等的连续线路视为一个子区间，并通过遗传算法为每个子区间搜索一个最优目标速度。

具体概述为：假设制动点位于第n个坡道，将制动点前每一个等坡度值的坡道距离视为一个子区间，则此线路区间集合为(s1, s2,…, sn−1, sn)，对应的目标速度集合为(v1, v2, …, vn−1, vn)。假设子区间限速为，则在第 i个子区间中，必须满足目标速度 vi≤。列车沿遗传算法搜索得到的速度序列运行，产生一条当前能耗最小的速度运行曲线，实现节能优化。

2.2 节能模型建立

列车在采用制动工况进站之前，其余线路上均采用牵引、匀速和惰行的操纵模式以达到节能目的，具体的工况选择由每个子区间的目标速度决定。假设第i个子区间的长度为si，目标速度即末速度 vi，则上一个子区间 si−1的目标速度 vi−1，即 si的初始速度。列车由 si−1末端加速或减速至目标速度vi后，再保持恒速运行到si末端，或者在si上一直匀速运行。

设子区间si中变速阶段的行驶距离为si1，恒速阶段的行驶距离为si2，则si=si1+si2。在第i个子区间，若列车以最大牵引力加速无法达到vi，或一直惰行减速也无法降至vi，则此目标速度vi无效，通过后续的遗传算法设计自动剔除并重新选择。坡道运行优化以列车安全、正点、精确停车等各项约束条件为前提，使得运行能耗最小。因此，节能模型目标函数为：

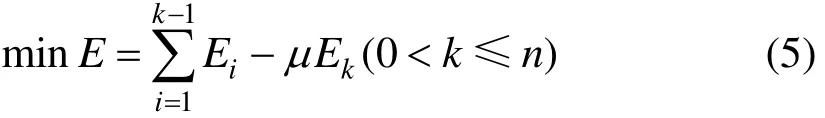
式中：Ei为区间si的能耗；Ek为制动区间sk的储能；μ为再生制动反馈能量的效率。

模型约束条件为：

式中：ti为区间si的运行时间；T为实际运行时间；v(x0)和 v(xs)为列车始末位置的速度；vi为区间 si的目标速度；为相应的限速；t为站间规定的运行时间；Δt为允许的时间误差。

模型解算过程如下。

1) 当 vi−1＜vi时，列车由 si−1末端加速至目标速度vi后保持匀速运行至si末端，则区间si的运行时间、能耗分别为：

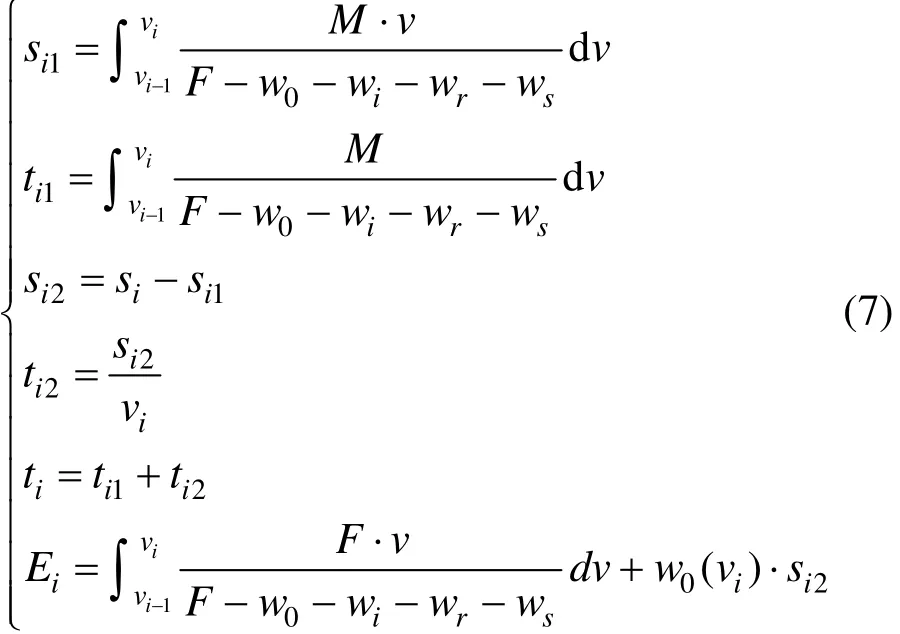
2) 当 vi-1= vi时，列车在区间 si上保持匀速运行，则运行时间、能耗分别为：

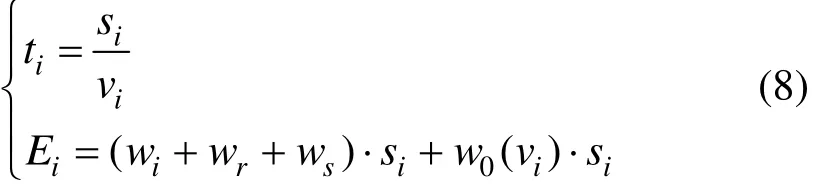
3) 当 vi-1＞ vi时，列车由si−1末端惰行减速至目标速度vi后保持匀速运行至si末端，则区间si的运行时间、能耗分别为：

为保证列车精确停车进站，本文中列车采用恒定减速度ab进行减速。设列车制动时速度为vb，制动距离为sb，制动点xb位于第k个子区间内，则制动工况的运行时间、储能分别为：

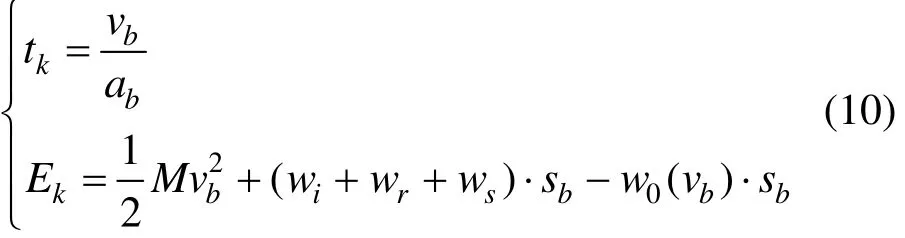
3 全线惰行优化

3.1 惰行优化操纵分析

本文中全线惰行优化是在坡道运行优化的基础上，在列车中间运行阶段，在一定速度范围内，于合适位置插入“牵引－惰行”工况转换点，再次使用遗传算法，搜索确定合理的惰行位置和相应的惰行速度，再次优化速度运行曲线。

2阶段优化一是充分利用线路坡度，根据坡道优化所得的区间目标速度来限制速度上下限，以惰行模式再次降低能耗并使列车的工况转换更加合理；二是列车在相对较小的速度波动范围内运行，避免了较大的速度波动给乘客带来的不舒适性。

3.2 节能模型建立

以坡道运行优化所得的速度距离曲线为基础，在列车运行的中间阶段 ( xin, xout)，通过遗传算法插入n个“牵引－惰行”工况转换点P1, P2,…, Pn，且xin＜P1＜P2＜ … ＜ Pn＜ xout，其中 ( xin, xout)是惰行优化的线路范围。则 ( xin, P1)是第 1个工况运行范围，为牵引状态；(P1, P2)是第2个工况运行范围，为惰行状态；… ( Pj-1, Pj)是第j个工况运行范围，直到列车运行至 xout位置时采用制动工况停车进站。

全线惰行优化充分利用惰行状态，在保证列车安全、正点、精确停车前提下，再次降低运行能耗，达到节能目的。假设2站间距离为s，列车始末位置分别为x0，xs，则列车启动加速阶段 ( x0, xin)的运行时间Tin，能耗Ein以及制动停车阶段 ( xout, xs)的运行时间 Tout，储能 Eout均由坡道运行优化得到。因此，节能模型目标函数为：式中：Ej为每个工况范围内的能耗；μ为再生制动反馈能量的效率。

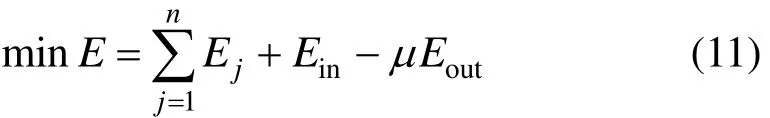
模型约束条件为：

式中：vj为每个工况运行范围内的速度；为相应的限速；tj为相应的运行时间。

模型解算过程如下：

1) 当 ( Pj-1, Pj)内为牵引状态时，列车的运行时间、能耗分别为：

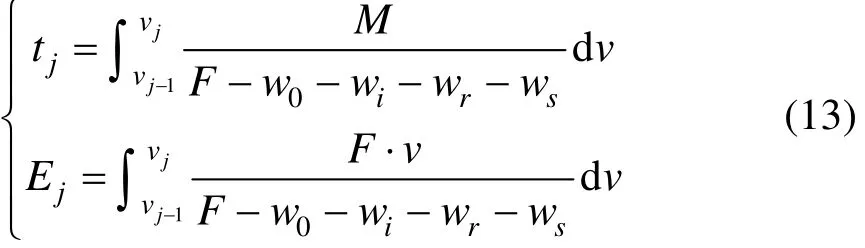
2) 当 ( Pj-1, Pj)内为惰行状态时，列车的运行时间、能耗分别为：

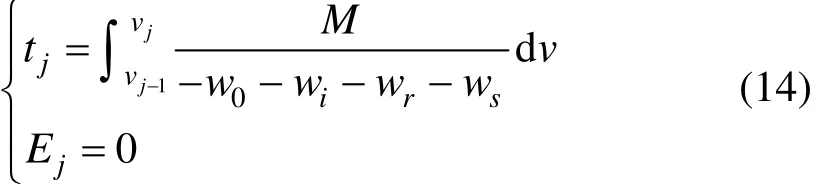
4 2阶段优化的遗传算法

本文建立的2个模型都属于非线性规划模型，且模型中涉及的运行时间、运行距离、能耗都通过微积分求解，模型求解难度较大。与精确算法寻找模型的收敛结果不同，遗传算法虽然不能保证一定能够找到最优解，但通过高效地迭代进化可以找到逼近最优解的满意解。第1阶段为坡道运行优化，目的是得到每个子区间的最优目标速度；第2阶段为全线惰行优化，以坡道运行优化后得到的速度曲线为基础，在列车运行的中间阶段搜索合理的惰行位置和惰行区间速度，再次优化列车速度曲线，达到节能优化的目的。

4.1 第1阶段算法设计

第1阶段优化的关键是获得坡道运行优化节能模型的最优解，算法具体步骤如下。

Step 1：染色体编码。采用二进制编码方式，染色体的长度适中。遗传算法的控制变量为等坡道值离散化后每个子区间的目标速度，一组目标速度序列用具有 n个基因的染色体 V =(v1, v2, ...,vn-1,vn)表示，在每个坡道限速范围内随机产生。

Step 2：种群产生。根据编码机制的定义，随机产生一定数目的染色体形成初始种群。种群规模介于50~200之间，在保证算法收敛速度的基础上，防止计算结果陷入局部最优。

Step 3：性能指标函数与适应度函数。针对生成的每一组目标速度序列，根据式(5)~(8)求解列车沿此速度序列运行的时间和能耗，若不满足第1阶段节能模型中的列车正点到站、限速及精确停车等约束条件，则此目标速度序列为无效序列，通过遗传算法中设置的惩罚函数自动剔除并重新选择。以能耗最小为优化目标，不再将实际运行时间误差考虑到性能指标中，则性能指标函数定义为：

式中：E为列车在2站间运行总能耗，且一定为正，则适应度函数为：

式中：A为程序设定的调整系数。

Step 4：采用轮盘赌算法进行选择操作，保证遗传算法终止时得到的最后结果是历代中出现过的适应度最高的个体。个体i被选择的概率pi为：

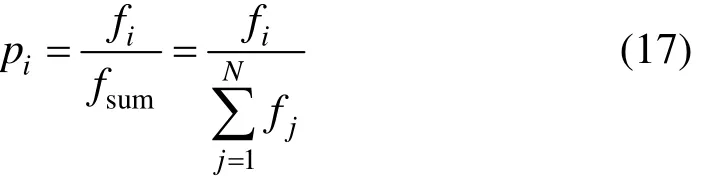
式中：fi为个体i的适应度；fsum为个体i所在子种群的总适应度；N为个体i所在子种群的大小。

Step 5：交叉操作采用单点交叉方式，交叉率为Pc。随机生成交叉位置k， k ∈(0,n)，则交叉后2个子代的染色体为：

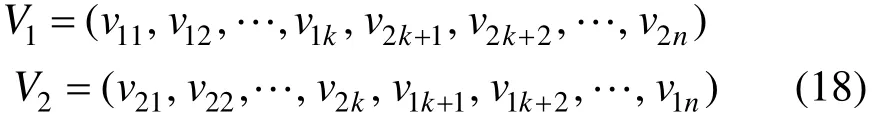
Step 6：变异操作采用随机单点变异方式，随机确定一个变异的基因，变异率为Pm。

Step 7：迭代次数加1，当达到最大迭代次数时，转入Step 8；否则转入Step 3。

Step 8：输出每个子区间对应的目标速度值。

4.2 第2阶段算法设计

第2阶段优化的遗传算法步骤与第一阶段优化的不同之处在于：Step1中控制变量为列车中间运行阶段“牵引－惰行”工况转换点位置，按照列车运行距离递增的顺序随机生成；Step 3中针对生成的每一组工况转换点位置 P = (P1, P2, … ,Pn-1, Pn)，根据式(10)~(11)求解列车沿此工况转换点位置运行的时间和能耗，同理若不满足第2阶段节能模型中的约束条件，则此组工况转换点无效，通过遗传算法中设置的惩罚函数自动剔除并重新选择。其他步骤均与第1阶段优化相同。

5 实例仿真

以济南−泰安城际铁路为仿真实例，线路全长为71.93 km，运行时间为(24±0.5) min，限速情况为200~350 km/h。以CRH3型动车组为研究对象，其主要参数特性见表1[12]。

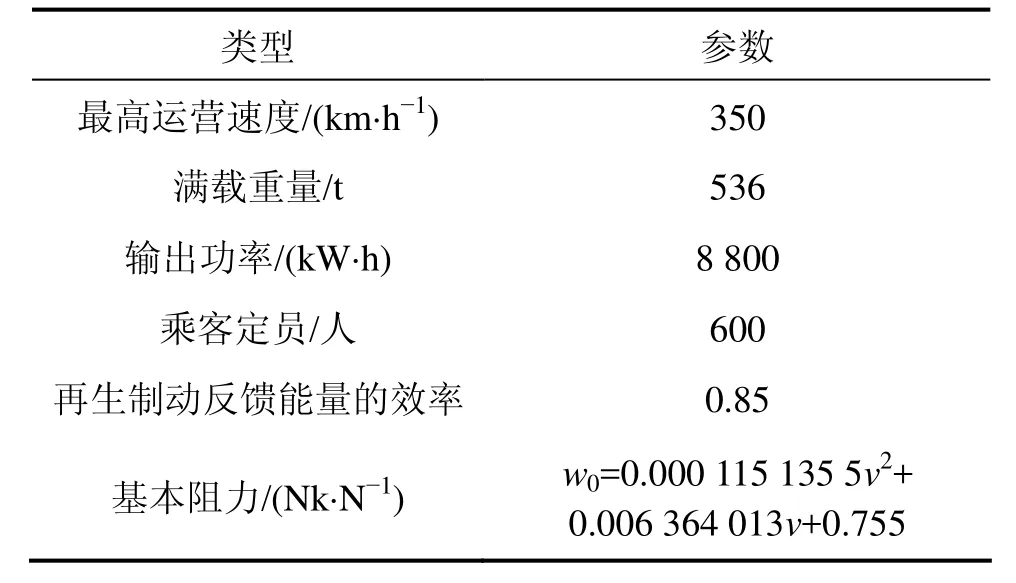
表1 CRH3动车组结构参数Table 1 Structural parameters of CRH3 train

为了说明本文优化方法的有效性，首先给出优化前的列车运行情况。此时，列车满足正点到站及限速约束，运行模式为牵引−匀速−惰行−制动，运用 MATLAB仿真得到的列车速度运行曲线如图 1所示。列车未优化前的运行时间为1 409.35 s，能耗为 4.70 428×109J。

在坡道运行优化仿真过程中，采用遗传算法搜索列车运行中每个子区间的目标速度，其中设置程序调整系数A为1015，种群的规模为100，交叉和变异的概率分别为0.7和0.007，迭代次数为300次。图2为染色体进化代数图，仿真结果如图3所示。列车的运行时间为1 436.79 s，能耗为4.35 730×109J。

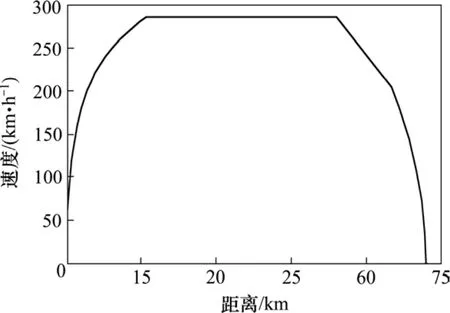
图1 未优化前列车的速度运行曲线Fig.1 Simulation result curve without optimization strategy

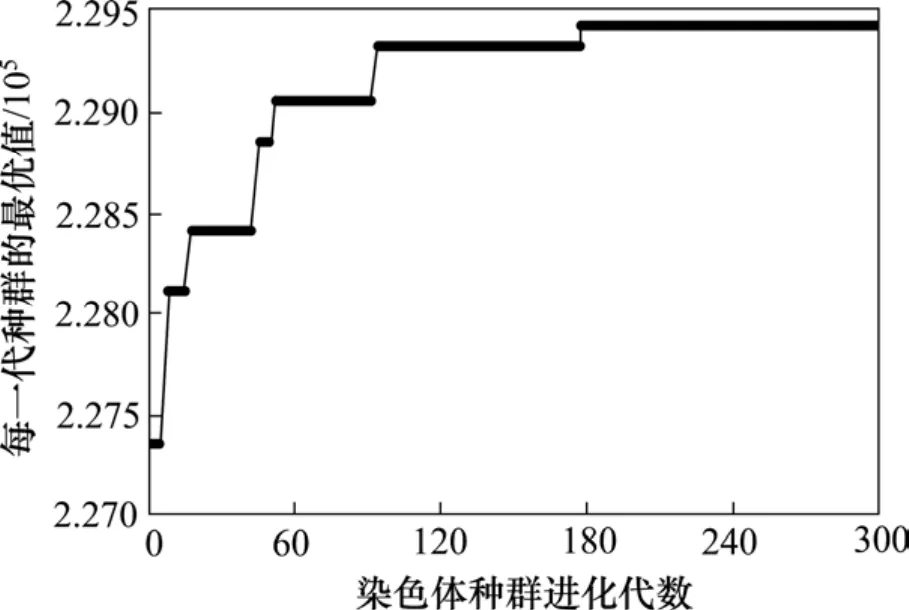
图2 染色体进化代数图Fig.2 Algebraic evolution of chromosomes

坡道运行优化速度曲线是在最优速度序列下，由上一个子区间牵引或惰行至当前子区间的目标速度后，再匀速运行至当前子区间的末端后得到。由图3可以看出，列车在中间运行阶段保持较大且相对平稳的运行速度。

在全线惰行优化仿真过程中，再次使用遗传算法，搜索惰行位置和惰行区间速度，线路数据、列车数据以及遗传算法参数保持一致。遗传算法搜索的惰行位置和惰行区间速度如表2所示，图4为染色体进化代数图，仿真结果如图5所示。列车的运行时间为1 460.81 s，能耗为4.15 717×109J。

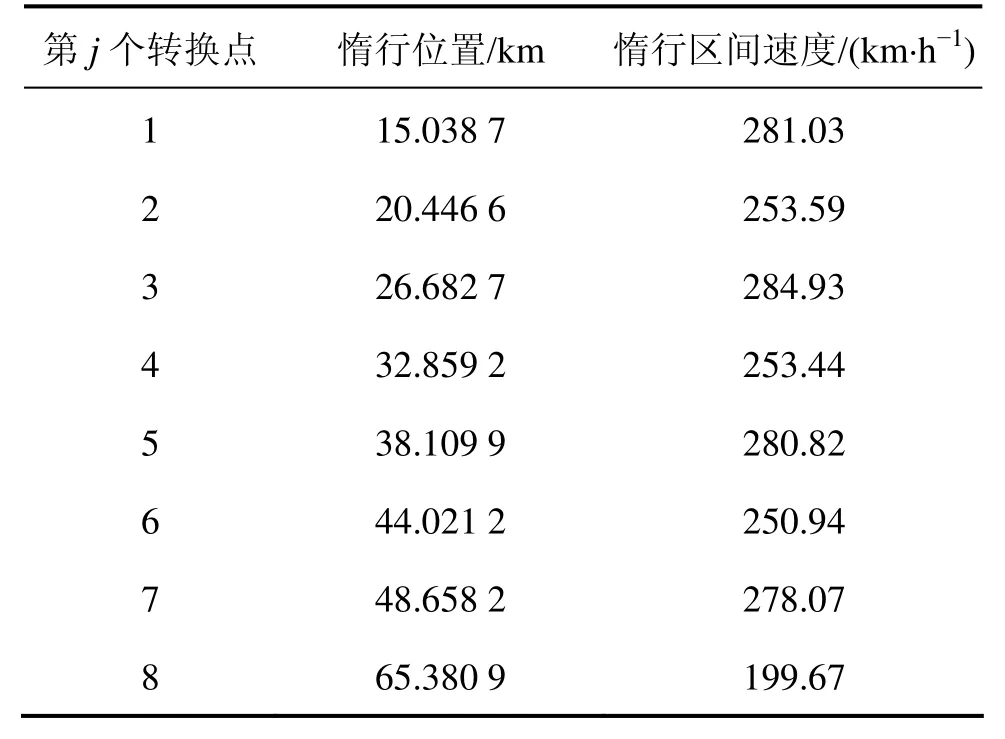
表2 中间运行阶段的惰行位置和区间速度Table 2 Coasting operation position and interval velocity of middle stage

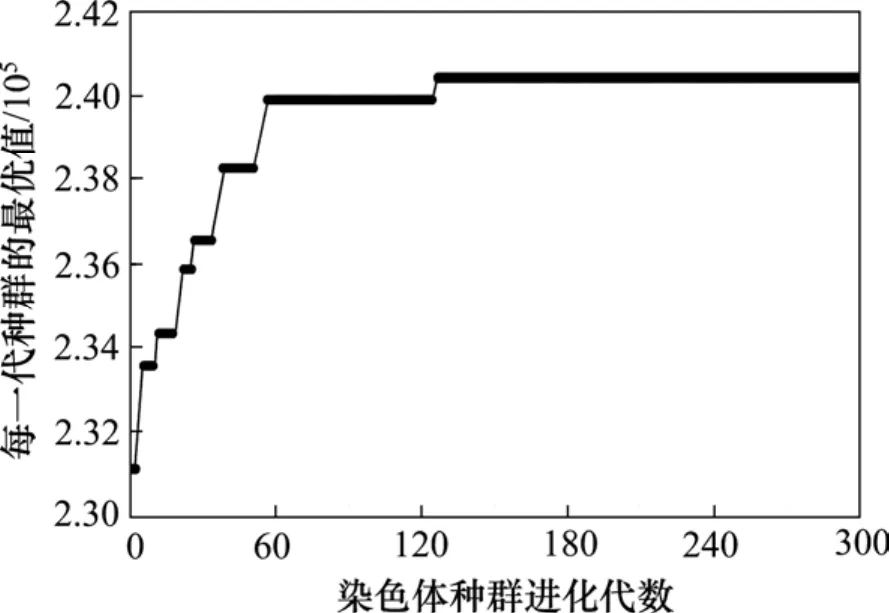
图4 染色体进化代数图Fig. 4 Algebraic evolution of chromosomes

列车在坡道运行优化和全线惰行优化下的运行时间、能耗以及节能比例的仿真数据如表3所示。

由表中3可知，优化后列车的运行时间有所增加，但是依然满足正点到站，且节能效果明显提升。全线惰行优化是以坡道运行优化为基础进行，再次优化速度运行曲线，节能效果达到11.63%。

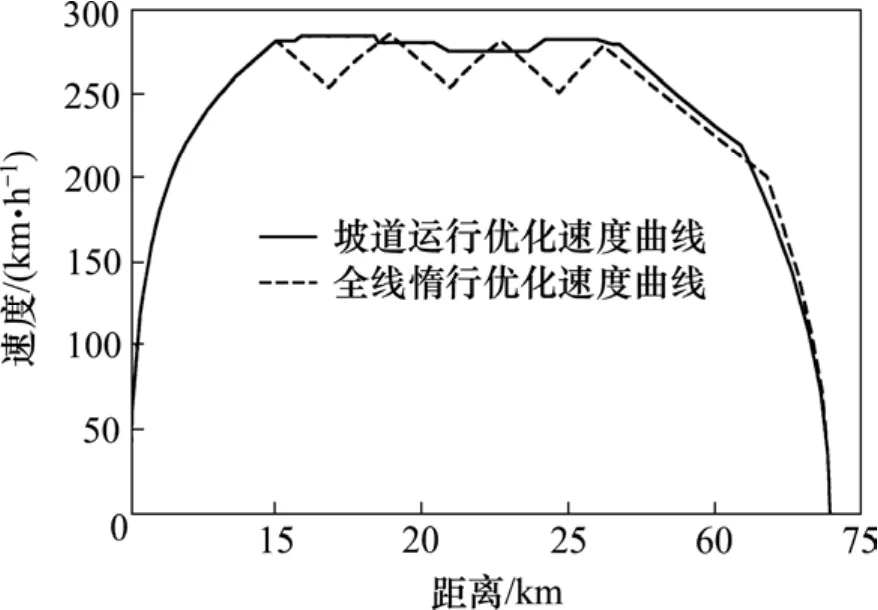
图5 全线惰行优化仿真曲线图Fig. 5 Simulation result curve of the whole coasting optimization

表3 仿真结果分析Table 3 Comparison of simulation results

6 结论

1) 以高速列车运行能耗最小为优化目标，考虑线路条件及再生制动储能，建立安全、正点、精确停车的站间列车节能模型，使得列车运行更加符合实际。

2) 提出包含坡道运行优化和全线惰行优化的2阶段优化方法。第1阶段将线路坡道离散化，通过遗传算法为每个子区间搜索一个适合的目标速度，将模型求解转化为最优化问题，同时避免了过多的决定参数设置；第2阶段再次使用遗传算法，在列车的中间运行阶段搜索合理的惰行位置和惰行速度，最终得到优化后的速度运行曲线。

3) 通过CRH3高速列车实例仿真可得，2阶段优化后列车节能效果达11.63%，验证了本文方法的有效性。今后随着计算机技术的发展和智能控制算法的改进，必将寻求新的启发式算法来提高运算速度和稳定性，并且结合仿真平台研究列车节能运行的在线优化。

参考文献：

[1] 陈涛. 高速列车运行能耗测算方法及其影响因素量化分析[D]. 北京: 北京交通大学, 2011.CHEN Tao. Traction energy consumption measuring methods study and quantification analysis on energy impact factors of high-speed train[D]. Beijing: Beijing Jiaotong University, 2011.

[2] 孙帮成, 李明商, 安超, 等. 高速列车综合节能技术讨论[C]// 2013年轨道交通电气与信息技术国际学术会议. 北京: 北京交通大学, 2013.SUN Bangcheng, LI Mingshang, AN Chao, et al.Discussion on integrated energy saving technologies of high-speed trains[C]// 2013 International Conference on Electrical and Information Technologies for Rail Transportation. Beijing: Beijing Jiaotong University,2013.

[3] Milroy I P. Minimum energy control of rail vehicle[C]//Proceeding of the Railway Engineer Conference, Sydney,Australia, Institution of Engineers, 1981.

[4] Chang C S, Sim S S. Optimizing train movements through coast control using genetic algorithms[J]. Proc of Electric Power Applications, 1997, 144(1): 65−73.

[5] Howlett. An optimal strategy for the control of a train[J].Journal of the ANZIAM, 1990, 31(5): 454−471.

[6] Howlett. The optimal control of a train[J]. Annals of Operations Research, 2000, 98(1): 65−87.

[7] Sicre C. Modelling and optimizing energy efficient manual driving on high-speed lines[J]. IEEJ Transactions on Electronic Engineering, 2012, 7(1): 633−640.

[8] 毛保华, 何天键, 袁振洲, 等. 通用列车运行模拟软件系统研究 [J]. 铁道学报, 2000, 22(1): 1−6.MAO Baohua, HE Tianjian, YUAN Zhenzhou, et al. A general-purposed simulation system on train movement[J]. Journal of the China Railway Society, 2000, 22(1):1−6.

[9] 丁勇, 毛保华, 刘海东, 等. 列车节能运行模拟系统的研究[J]. 北方交通大学学报, 2004, 28(2): 76−81.DING Yong, MAO Baohua, LIU Haidong, et al. Study on train movement simulation for saving energy[J]. Journal of Northern Jiaotong University, 2004, 28(2): 76−81.

[10] 崔恒斌, 冯晓云, 王青元, 等. 制动利用率对高速列车节能操纵策略的影响[J]. 铁道学报, 2012, 34(8): 13−18.CUI Hengbin, FENG Xiaoyun, WANG Qinyuan, et al.Influence of braking efficiency on high-speed train energy-saving driving strategies[J]. Journal of the China Railway Society, 2012, 34(8): 13−18.

[11] 王青元, 冯晓云, 朱金陵, 等. 考虑再生制动能量利用的高速列车节能最优控制仿真研究[J]. 中国铁道科学,2015, 36(1): 96−102.WANG Qinyuan, FENG Xiaoyun, ZHU Jinling, et al.Simulation study on energy-saving optimal control of high-speed train considering regenerative braking energy utilization[J]. Journal of China Railway Science, 2015,36(1): 96−102.

[12] 宋文婷, 谭觅. 高速列车的节能操纵策略研究[J]. 铁道科学与工程学报, 2016, 13(3): 18−25.SONG Wenting, TAN Mi. Research on energy-saving operation strategy for high-speed train[J]. Journal of Railway Science and Engineering, 2016, 13(3): 18−25.

[13] 中华人民共和国铁道部. 列车牵引计算规程[M]. 北京:中国铁道出版社, 1999.Ministry of Railways of the People’s Republic of China.Train traction calculation procedure[M]. Beijing: China Railway Press, 1999.

[14] 毛保华. 列车运行计算与设计[M]. 北京: 人民交通出版社, 2013.MAO Baohua. Calculation and design of train operation[M]. Beijing: China Communication Press, 2013.