区域经济增长与最优城市首位度的实证研究

李宝礼，胡雪萍

（1.安徽科技学院 财经学院，安徽 蚌埠 233100；2.中南财经政法大学 经济学院，武汉 430073）

0 引言

城市首位度通常是指用来衡量一个国家或地区生产要素特别是人口要素空间分布状况的重要指标，能够在一定程度上反映一个国家或地区的城市体系在吸引外资、提高劳动生产率、降低运输成本以及集聚资本和人力资源等方面的情况。城市首位度的概念最早由Jefferson提出，他在研究国家城市规模分布时，将一个国家人口最多的城市定义为首位城市，将城市首位度定义为首位城市与第二位城市的人口数量之比。本文借鉴Jefferson城市首位度的定义，并将其应用于省域层面，以各省人口第一位城市与第二位城市的人口规模比值定义各省的城市首位度。

城市首位度的概念与城市集聚高度一致，较高的城市首位度意味着生产要素在空间分布上向区域的首位城市集中。城市首位度越高，城市集聚效应引致的知识积累、技术创新和规模经济的效应越大，从而越有利于经济增长；但是要素向区域内首位城市的过度集聚也会带来城市交通拥挤、污染、疾病传播等大城市病问题，造成城市集聚不经济，阻碍经济增长。因此，是否存在一个最优的城市首位度值以最大化经济增长率，国外学界对此有一定的研究。

Williamson（1965）[1]指出城市聚集在经济发展的早期阶段有利于经济增长，随着经济发展水平的提高，城市集聚造成交通拥挤、环境污染、疾病传播等大城市病的突现阻碍经济增长；Henderson（2003）[2]通过对70个国家数据的实证研究，发现了城市首位度对经济增长的影响呈非线性形式，证实了存在最优城市首位度这一问题；Brulhart和Sbergami（2008）[3]分别利用105个国家的大样本面板数据与欧洲15个国家的小样本面板数据，通过实证研究发现，城市首位度对经济增长的影响与一个国家或地区的初始经济发展水平有关。Steven 和 Frederick（2008）[4]以 Henderson模型为基础，将FDI作为连接城市首位度与经济增长的纽带，实证结果表明不存在最大化经济增长率的最优城市首位度，并进一步认为即使城市首位度与经济增长之间有非线性关系，可能存在的也是最差城市首位度而非最优城市首位度。

考虑到我国将发展经济的权利下放到省级行政单位，且不同省份间的人口、资源和自然环境差异较大，本文将城市首位度的概念由国家层面扩展到省区层面，研究各省区城市首位度与区域经济增长之间的内在机制。并以此为基础构建最优城市首位度公式，利用计量回归参数测算出各省区最优城市首位度门限值。同时，探究各省区实际城市首位度对最优城市首位度遵循或偏离背后的内在逻辑，以及对区域经济可持续增长的影响。

1 计量模型、变量选择与数据描述

1.1 计量模型

本文采用柯布-道格拉斯生产函数形式构建城市首位度对区域经济增长的贡献。

其中，Ki(t)为i地区t时期的资本存量。Ni(t)为t时期i地区的就业人数；Ai(t)为t时期i地区的技术水平；α表示资本产出弹性。将(1)式总量生产函数转换为人均产出函数，取对数并进行差分变换得到(2)式：

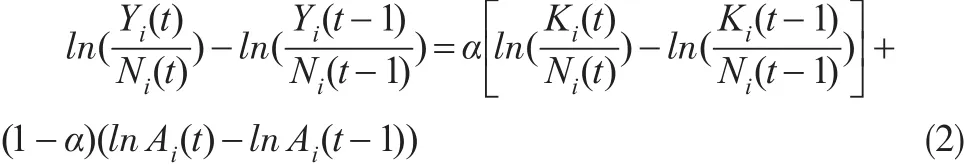
从(2)式中可以看出，区域人均产出增长率取决于人均资本存量增长率与技术进步率。接下来本文将城市首位度引入(2)式，以捕捉技术进步变动路径的微观机制。

Berliant和Fujita（2010）[5]在对城市集聚经济的分析中引入了知识分工的概念，指出城市集聚提高了知识分工的广度和深度。城市集聚对知识创造和传播的正向影响促进了城市的技术创新。

根据城市集聚对技术创新的微观机制的影响，可以将(2)式中技术进步表示如下：

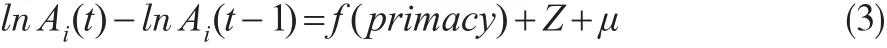
(3)式中，primacy表示城市首位度作为城市集聚的替代变量，Z为控制变量，μ为随机变量。f(·)的具体形式取决于城市首位度对技术进步的影响机制。通过前文的分析可知，城市聚集对技术进步存在正向影响，但是过度的城市集聚提高了城市的生活成本，迫使大量资源从创新活动转移到用于改善个体的生活质量，阻碍了技术进步，因此城市集聚对技术进步的影响是连续非线性的。考虑到区域城市首位度的高低与不同区域的初始经济发展水平、收入分配状况、自然环境等区域异质性因素的变化有关，本文将f(·)的具体形式定义如下：

将(3)式和(4)式结合并代入(2)式，以构建本文的基础模型。如(5)式所示：

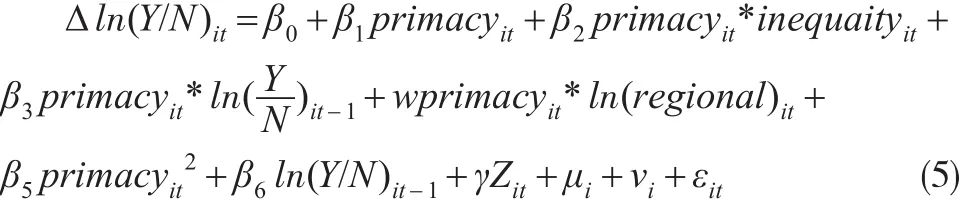
下标i和t分别表示省区和年份，因变量为劳均产出增长率；inequaityit为区域基尼系数；regionalit为区域异质性变量，用区域国土面积和人口规模表示；w为待估参数；Zit表示控制变量向量；μi和vi分别表示个体效应和时间效应项；εit为随同误差项。

本文将最优城市首位度定义为能够带来最大化劳均产出增长率的城市首位度，据此定义，对(5)式进行最优化处理，可得最优城市集聚度计算公式如下：

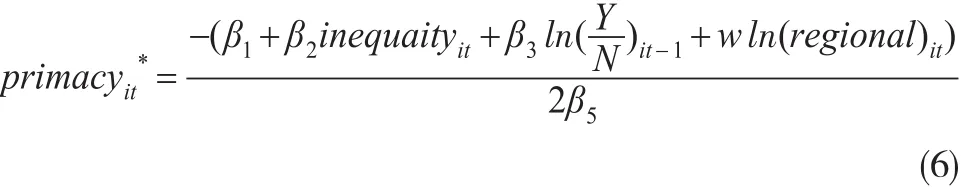
根据前文的分析，经济增长与城市集聚之间并非是线性的，二者应成倒U型关系，因此预计待估参数β5＜0，β1＞0；其他变量参数估计结果的方向有待验证。

1.2 变量与数据说明

基于(5)式，并结合我国各地区的实际情况和统计数据的可获得性，本文选择的指标（见表1）和相应的数据来源如下，样本剔除了北京、上海、天津和重庆4个直辖市数据，由于山东、西藏、吉林和海南4个省个别年份数据缺失，也将其剔除。于是本文的研究样本为全国23个省市自治区2005—2014年的面板数据。数据来源《中国统计年鉴》（2006—2015）、《中国城市统计年鉴》（2006—2015）以及各省统计年鉴，农村数据部分来源于《中国农村住户调查年鉴》（2006—2010）。

表1 变量与指标说明

1.3 变量描述

（1）劳均产值指标

图1为不同年份我国各省区劳均产值的核密度图。从2005—2009年直至2014年我国不同省区劳均产值的变化趋势可以看出，我国劳均产值随着时间的向前推移，核密度图不断向右移动，表明我国劳均产值指标的均值呈动态递增的态势。这说明近年来我国不同省区的劳均产值均取得了一定程度的增长，经济发展水平显著提高。但同时应当看到，我国劳均产值核密度图的分散度亦随着时间的向前推移在不断扩大，这说明近年来我国不同省区之间的劳均产值差距不仅没有缩小，反而呈进一步扩大趋势，区域经济发展失衡现象仍在加剧。

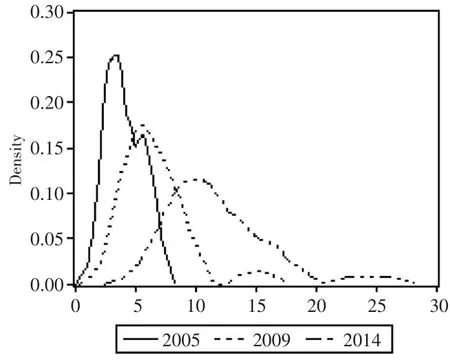
图1 劳均产值指标核密度图

（2）城市首位度指标

图2为我国不同年份各省区城市首位度核密度图。从中可以看出，我国城市首位度的均值随着时间的向前推移，核密度图向右移动，但移动幅度较小，说明我国不同省区城市首位度均值呈缓慢递增的态势，这与我国近年来实施的限制大城市规模，鼓励中小城市发展的城市发展战略有关。图2的另一个突出特征表现为不同年份的核密度图的分散度较大，这说明我国不同省区的城市首位度差异明显。从实际城市首位度样本数据的空间分布来看，城市首位度与区域经济发展水平呈反向变化关系，西部地区省份的城市首位度总体高于中部和东部地区。

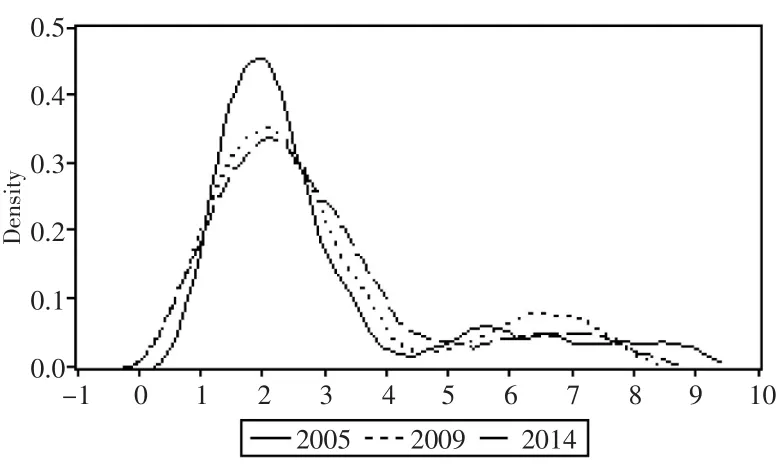
图2 城市首位度指标核密度图

2 实证结果分析

2.1 城市首位度对区域经济增长的影响

(5)式为本文实证研究的基础模型，考虑到劳动生产率与城市首位度之间存在的内生性问题，为了降低模型内生性可能带来的回归结果的偏误或非一致性，本文采用了工具变量广义矩估计（IV-GMM）。工具变量选取须遵循两个原则：一是工具变量与模型随机误差项不相关；二是工具变量与内生解释变量即城市首位度高度相关。基于此，本文借鉴黄玖立（2006）[7]的做法，选取各省首位城市到海岸线距离的倒数作为工具变量。

由于区域劳动生产率具有自我强化机制，当期区域劳动生产率水平会影响下一期劳动生产率，因此，本文还以劳动生产率的一期滞后作为自变量，构建动态面板模型。为了检验回归结果的稳健性，本文同时给出了固定效应模型的回归结果，回归结果如表2所示。

从表2中可以看出，固定效应、工具变量GMM、系统GMM的三组回归系数的回归结果的符号和显著性大致相同，显示了回归结果的稳健性。城市首位度（primacy）系数在三组回归结果中全部显著为正，说明各省区城市首位度对区域经济增长具有正向作用，城市首位度的二次方项在所有的回归结果均为负，并且在5%以上的显著性水平上显著，表明城市首位度对区域经济增长的影响并非是线性的，而是呈倒U型。这表明，生产要素不断向区域内首位城市集中，要素集聚产生的溢出效应和规模经济效应使得首位城市的示范与带动作用得到充分发挥，引领区域经济增长。然而，随着城市首位度越过最优门槛值，集聚效应引致的区域生产要素向首位城市的进一步集聚，一方面，使得首位城市的生产成本加速递增，由集聚经济转向集聚不经济，降低了首位城市的生产效率；另一方面，生产要素由区域内其他城市向首位城市流动，弱化了其他城市的经济增长潜力，加之首位城市拥有较强的行政力量，制约了首位城市向其他城市的扩散效应，最终导致了区域经济增长的减缓，实证结果与Williamson假说一致。

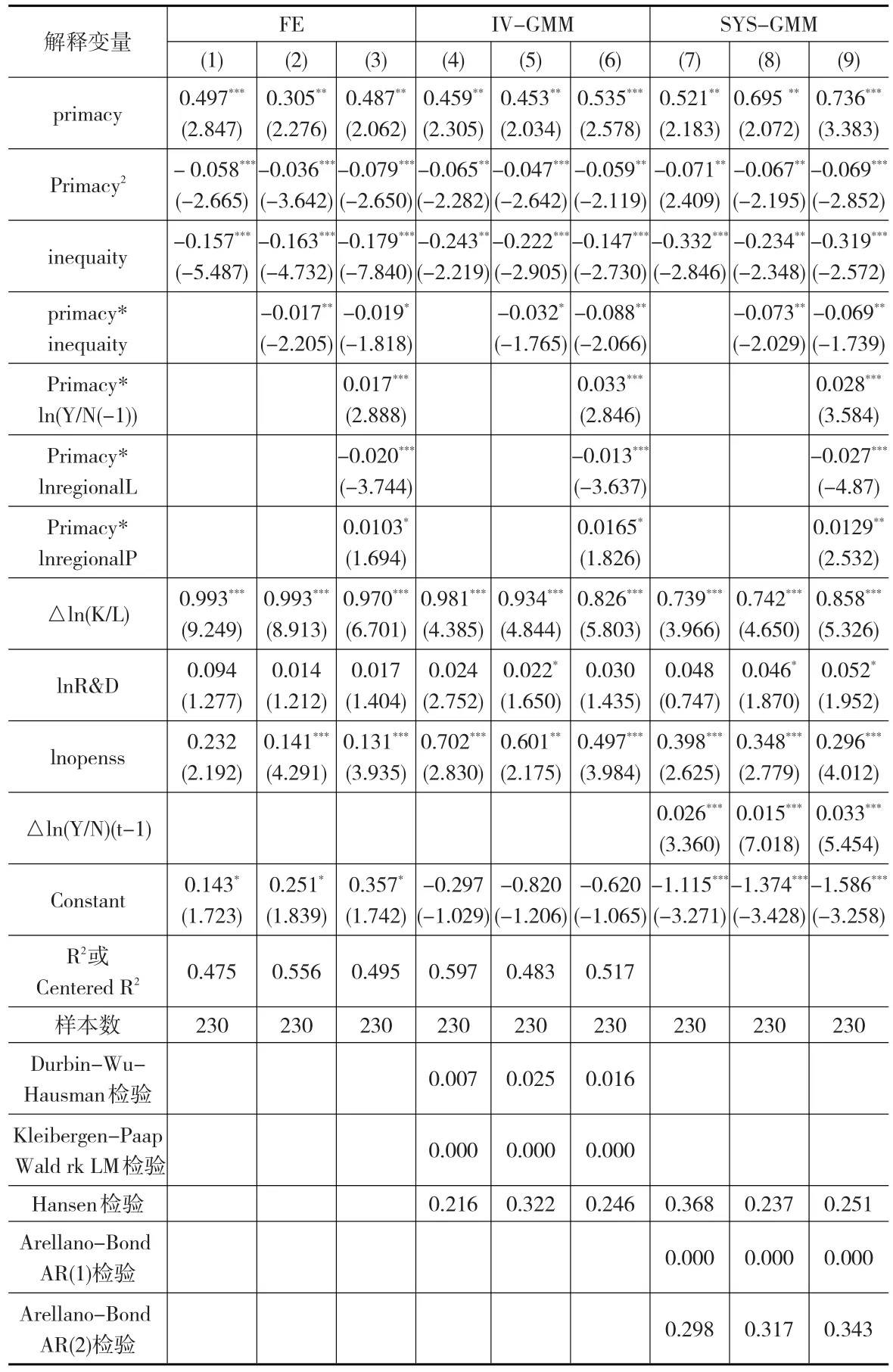
表2 实证回归结果

设定表2中模型(3)、模型(6)和模型(9)中进一步引入了城市首位度与初始经济发展水平交叉项、城市首位度与省区行政面积交叉项以及城市首位度与省区人口规模交叉项。回归结果显示，城市首位度与初始经济发展水平交叉项显著为正，表明城市首位度对经济增长的作用受初始经济发展水平的影响，较高的初始经济发展水平能够提高城市首位度对经济增长的正向影响，实证结果与Fallah等人的观点一致。城市首位度与省区行政面积交叉项显著为负，说明距离在城市首位度对经济增长影响中的作用并不是无关紧要的，中心城市对区域内其他城市的边际辐射带动作用会随着距离的递增而衰减。城市集聚与省区人口规模交叉项回归结果显著为正，这表明城市首位度对区域经济增长的作用受到地区人口规模的影响，人口规模越大将使得城市集聚对区域经济增长的影响增强，由人力资本内嵌于社会个体成员之中，社会人力资本总量等于个体人力资本投资的水平加总，人口规模与人力资本积累是正相关的；同时，人口规模越大，拥有异质性知识的劳动力的数量越多，异质性知识的劳动者之间的知识分工和协作的规模和范围也在扩大，加速了知识的积累和技术创新。因此，城市首位度与地区人口规模交叉项的实证结果在逻辑上与理论是自洽的。

收入不平等（inequaity）在三组回归结果中的符号均为负，并在较高的显著性水平上通过检验，说明我国区域经济增长已经跨越了依靠物质资本积累推动经济增长的初始阶段，经济增长越来越受制于人力资本积累和技术创新水平。收入不平等对人力资本积累和技术创新的负面影响阻碍了经济增长，实证结果证实了这一理论假说。在设定表2中模型(2)、模型(5)和模型(8)中加入了城市集聚与收入不平等的交叉项，三组回归结果均显著为负，这表明，城市首位度对区域经济增长的影响受收入不平等的影响，在相同城市集聚度情况下，收入分配不平等的扩大将使得城市首位度对经济增长的影响减弱。实证结果的内在逻辑是，收入不平等迫使政府将更多的生产性资源用于维护社会稳定，提供公共物品等非生产性用途，并且收入不平等加剧了城市内社会阶层的分化与对立，削弱了社会凝聚力，不利于人力资本积累与知识溢出，降低了城市集聚经济的规模和效率。

表2的回归结果显示，控制变量的回归系数符号与理论是一致的。其中，人均资本增长率（△ln(K/L)）对区域经济增长的贡献在所有设定中均显著为正，并且系数值较大，这与我国长期以来过度依赖固定资产投资拉动经济增长的现状一致。R&D从业人员数量仅在设定表2中模型(5)、模型(8)和模型(9)中10%的显著性水平下显著，且系数值较小，说明虽然人力资本对各省区经济增长具有正向作用，但其潜能还没有得到充分发挥，未来还具有较大的提升空间。经济开放度（lnopenss）指标在所有的模型设定中均显著为正，说明经济开放度越高越有利于吸引国外的资金、技术和管理经验，促进本地经济增长，该结论已得到大多数研究成果的证实。

2.2 最优城市首位度

从表2的回归结果可知，城市首位度指标的一次项回归结果为正，二次项回归结果为负，说明城市首位度对经济增长的影响为非线性的，且呈倒U型，结果表明存在最优城市首位度门槛值以最大化区域经济增长率。表2中模型(3)、模型(6)和模型(9)中所有交乘项的回归结果均显著，说明各省最优城市首位度受交乘项的影响。将模型(3)、模型(6)和模型(9)中的相关参数估计结果代入(6)式，并结合各省的相关数据计算出各自的最优城市首位度，最后将计算结果表示在下页图1中，其中横轴表示年份，纵轴表示城市首位度。考虑到我国东中西部地区经济与城市发展水平存在较大差距，为了更深入分析不同区域实际城市首位度与最优城市首位分布差异，将23个省区按照东、中、西部的所属划分为东部、中部和西部三个经济区域。如下页图3所示。

从图3(a)中可以看出，除辽宁、广东、福建三省外，东部地区各省城市首位度实际值与最优值之间均呈收敛趋势。其中江苏省的最优城市首位度与实际城市首位度之间的耦合度最高，广东省的城市首位度实际值与最优值之间的差距最大，从整体看，东部地区城市首位度实际值低于最优值。东部地区作为改革开放的前沿，借助政策和地理优势成为吸引外资的首先之地，出现了一批沿海开放城市，并逐渐取代各省的省会城市，成为区域经济中心，使得沿海省份形成了以省会城市为代表的政治文化中心和以沿海开放城市为代表的经济中心的“双中心”格局，如沈阳-大连、石家庄-唐山、南京-苏州、杭州-宁波、福州-厦门、广州-深圳等。东部地区“双中心”格局的形成改变了区域内人口向省会城市集聚的传统，在市场力量的作用下，新兴城市分流了首位城市的要素流入，造成了东部地区形成了实际城市首位度较低局面。

东部地区产业结构主要以技术含量较低的加工制造业为主，东部地区城市利用各自的比较优势，形成多点开花的经济发展格局，充分节约了要素流动过程中的交易成本，促进了区域经济增长。但是随着经济发展水平的提高，东部地区要素禀赋结构正在发生变化，劳动力成本显著提高，资本不再是稀缺资源，根据原有要素禀赋结构建立的劳动密集型加工制造业的产业结构的竞争优势已不复存在，落后的产业结构已经成为拖累该区域经济增长的首要因素，东部地区的产业结构亟待转型升级。

本文认为东部地区的“双中心”甚至“多中心”城市发展格局不利于产业结构转型升级，其原因在“双中心”城市之间对人才和技术的竞争削弱了城市的集聚效应。受行政体制的影响，东部地区各省会城市既是区域的政治和文化中心又想成为区域的经济中心，省会城市通过强大的政治影响力，动用行政力量尽可能的将区域内优质要素揽入其中，而区域经济强市在竞争中也不甘势弱，依靠其雄厚的经济实力，运用市场力量，通过提高要素回报率来吸引优质要素向其集聚。在行政力量与市场力量的恶性竞争下，各种同质化的总部经济区、技术研发中心在东部省份内遍地开花，不仅造成了资源的严重浪费，而且极大弱化了要素集聚对城市知识积累和技术创新的协同和溢出效应。因此，协调首位城市与其他城市间的功能定位，提高首位城市的要素集聚度，对提高东部地区各省的技术创新和科技研发能力，促进产业结构的优化升级和区域经济的可持续增长具有重要意义。

图3（b）和（c）分别表示中部与西部地区城市首位度实际值与最优值走势图，与东部地区相比，中西部省份城市首位度实际值与最优值之间的差距较大，且普遍呈实际值高于最优值的态势，表明中西部地区各省区城市首位度过高。造成这一现象的可能原因如下：首先，从本文构建的最优城市首位度模型看，由于中西部地区收入不平等程度高于东部地区、初始经济发展水平低于东部地区且行政区面积较大，使得根据(6)式及表2的回归结果计算的中西部城市首位度的最优值较东部地区偏低。其次，中西部地区省份的首位城市全部为各自的省会城市，省会城市不仅是各自的政治文化中心，也是区域的经济中心，计划经济时期，中西部地区各省区除省会城市之外，省内其他城市的经济基础较差，国家的计划投资主要流向各自的省会城市；改革开放后，中西部地区的省会城市依赖其良好的经济基础设施以及强大的行政特权在吸引境内外资本的竞争中依然占据绝对的主导权。在“马太效应”作用下，中西部地区各省会城市与省内其他城市之间的经济发展鸿沟越拉越大，省会城市的经济总量处于绝对的领先地位，部分省会城市的经济总量占据全省的半壁江山。

图3 东中西部地区各省历年实际城市首位度与最优城市首位度

与东部地区不同，中西部地区的经济发展还处于中低水平阶段，劳动力密集型的加工制造业在中西部地区仍然具有比较优势，中西部地区各省的其他城市具有承接此类产业的能力和优势，不必全部向省会城市集聚。然而图3（b）和（c）却表明，中西部地区，尤其是西部地区城市首位度实际值远高于最优值，这意味着中西部地区存在要素向首位城市过度集聚的状况，这种状况虽然带来了首位城市的繁荣，但这样的繁荣却是以其他城市的经济停滞甚至塌陷为代价的，这样的城市发展格局对区域整体经济增长来说，显然是不平衡，不可持续的。

3 结论

根据实证研究结果，可以得出我国城市首位度与区域经济增长之间的关系有如下特征：（1）城市首位度对区域经济增长的影响为非线性形式；（2）城市首位度对经济增长的作用受初始经济发展水平的影响，较高的初始经济发展水平能够提高城市首位度对经济增长的正向影响；（3）首位城市对区域经济增长的作用与省区行政面积负相关，说明首位城市对区域内其他城市的边际辐射带动作用会随着距离的递增而衰减；（4）城市首位度对区域经济增长的影作用受到地区人口规模的影响，人口规模越大将使得城市集聚对区域经济增长的影响增强。从历年实际城市首位度与最优城市首位度的变动趋势看，东部地区城市首位度实际值与最优值之间的耦合度最高，中部地区次之，西部地区城市首位度实际值与最优值之间的偏离度最大。总体看，东部地区城市首位度实际值低于最优值，中西部地区城市首位度实际值高于最优值。

参考文献：

[1]Williamson J G.Regional Inequality and the Process of National De⁃velopment[J].Economic Development and Cultural Change,1965,(4).

[2]Henderson J V.The Urbanization Process and Economic Growth:The So-What Question[J].Journal of Economic Growth,2003,(8).

[3]Brulhart M，Sbergami F.Agglomeration and Growth:Cross-Country Ev⁃idence[R].No6941,CEPR,London,2008.

[4]Steven P，Frederick P.Growth,Foreign Direct Investment and Urban Concentrations:Unbundling Spatial Lags[R].No195,DNB,Netherlands,2008.

[5]Berliant M，Fujita M.Dynamics of Knowledge Creation and Transfer:the Two Person Case[J].The International Society for Economic Theo⁃ry,2009,(2).

[6]陈昌兵.各地区居民收入基尼系数计算及其非参数计量模型分析[J].数量经济与技术经济研究,2007,(1).

[7]黄玖立,李坤望.出口开放、地区市场规模和经济增长[J].经济研究,2006,(6).