卫星定位中坐标转换研究

季赛玲

（江苏无线电厂有限公司，江苏 南京 210012）

1 概述

卫星定位是一种利用卫星对某个物体进行准确定位的技术，在任意时刻、地球上的任意点，只要同时能观测到4颗卫星，即可实现定位、导航、授时等功能。卫星定位可以用来引导飞机、船舶、车辆及个人，沿着设定的路线，安全、准确、准时到达目的地。目前，成熟的卫星定位系统有美国的全球定位系统（Global Positioning System，GPS），俄罗斯的全球卫星导航系统（Global Navigation Satellite System，GLONASS），中国的北斗系统和欧洲的“伽利略”。

由卫星定位的基本原理可知，卫星定位是以绕地球运行的卫星为动态已知点，以根据电磁波传播时间求得卫星接收机观测的星站距离，进而来确定接收机或测站的位置[1]。因此，位置的确定离不开坐标系。

2 坐标系

众所周知，确定卫星的位置一般使用天球坐标系，确定地面的位置则需要用地球坐标系。地球坐标系是与地球体相固联的坐标系。常用的地球坐标系有大地坐标系、空间直角坐标系、高斯直角坐标系。

2.1 大地坐标系

比照各卫星定位系统的信息输出协议，均使用大地坐标系。大地坐标系是大地测量的基本坐标系，是大地计算的基础，常用于研究地球的形状、大小，编制地图，火箭和卫星发射及军事方面的定位及运算等方面。

大地坐标系是大地测量时以参考椭球面为基准建立起来的坐标系。大地坐标系的确立包括选择一个椭球，对椭球进行定位和确定大地起算数据。参考椭球是一个大小、形状和定位、定向都已确定的地球椭球。它使用大地经度L、大地纬度B和大地高H表示地面点的位置。过地面点P的子午面与起始子午面间夹角交称为P点的大地经度。由起始子午面算起，向东为正，称东经（0°～180°），向西为负，叫西经（0°～-180°）。P点的大地纬度则是经过P点的椭球法线与赤道面的夹角。由赤道面算起，向北为正，叫北纬（0°～90°），向南为负，叫南纬（0°～-90°）。从地面点P沿椭球法线到椭球面的距离称为大地高，如图1所示。

2.2 空间直角坐标系

空间直角坐标系常用于不同参照椭球体的坐标转换。例如WGS84与CGCS2000坐标转换时，首先需要WGS84的大地坐标转换成空间直角坐标，然后才能换算参数，最后转换成CGCS2000的坐标[2]。空间直角坐标系的坐标原点位于地球质心（地心坐标系）或参考椭球中心（参心坐标系），z轴指向地球北极，x轴指向起始子午面与地球赤道的交点，y轴垂直于xoz面并构成右手坐标系。P点的空间直角坐标可以用该点在此坐标系的各个坐标轴的投影表示，如图1所示。

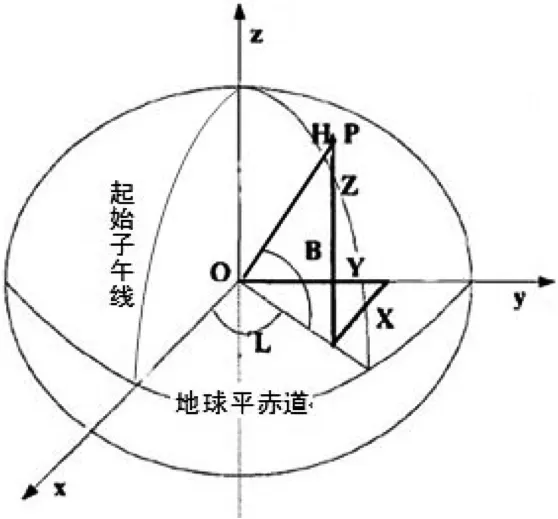
图1 坐标系示意

2.3 高斯直角坐标系

高斯直角坐标系，是大地测量、城市测地、各种工程测量和地图制图中广泛采用的一种平面坐标系。大地坐标是一种椭球面上的坐标，若将其直接用于工程规划、设计、施工等很不方便，不能直接应用于测图。因此，需要将大地坐标按一定的数学规律转换为平面直角坐标，使测量、计算和绘图更加方便。

目前我国采用的是高斯投影，是由数学家高斯提出，克吕格改进的一种分带投影方法。具体方法是将地球按经线划分为带，称其为投影带。投影是从子午线开始，分6°带和3°带两种。每隔6°划分一带的叫6°带，每隔3°划分一带的叫3°带。

我国领土位于东经72°—136°之间，共包括了11个6°带，即13—23带；22个3°投影带，即24—45带。通过高斯投影，把中央子午线的投影作为横坐标轴，用x表示；把赤道的投影作为纵坐标，用y表示；把x轴和y轴的交点作为坐标原点[3]。由此构成的直角坐标系称为高斯直角坐标系，如图2所示。

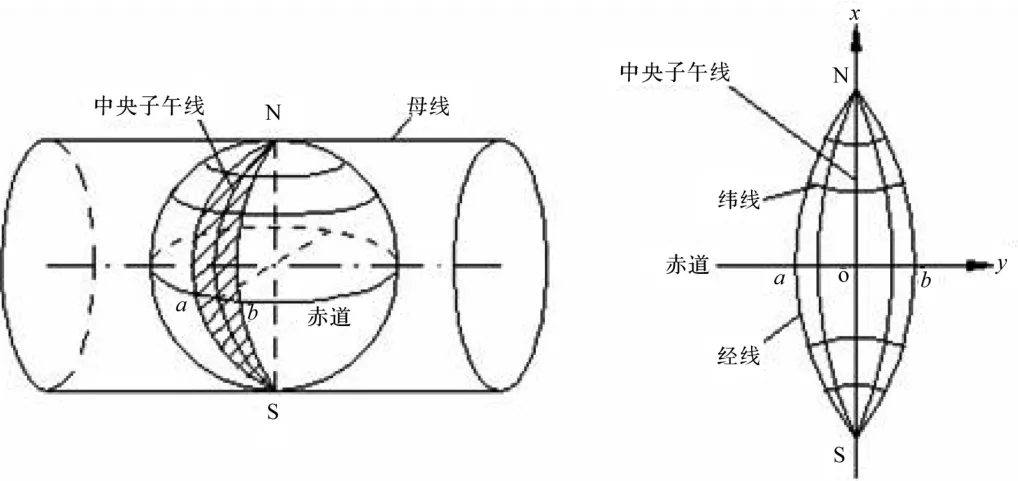
图2 高斯投影

3 转换模型

本文主要讨论相同的椭球模型下的坐标转换，不涉及不同坐标系统之间的转换。

3.1 大地坐标与空间直角坐标的转换

地面任意一点P的位置，可用大地坐标表示为（B，L，H），空间直角坐标表示为（X，Y，Z）如图1所示。其中：大地纬度B—过地面点的椭球面法线与椭球赤道面的夹角；大地经度L—过地面点的椭球子午面与格林威治平大地子午面之间的夹角；大地高H—地面点沿椭球面法线到椭球面的距离；X，Y，Z—地面点在空间直角坐标系x，y，z轴的投影。

这两种坐标的换算关系为：

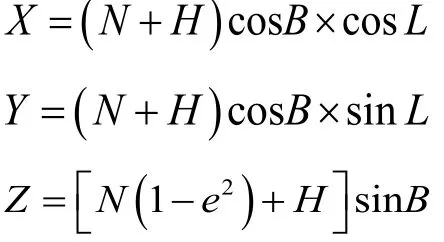
式中，N为椭球的卯酉圆曲率半径；e为椭球的第一偏心率。它们的表达式为：

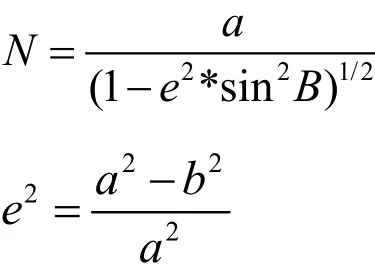
式中，a为椭球长半径；b为椭球短半径。

当需要由空间直角坐标换算大地坐标时，可采用下式计算：

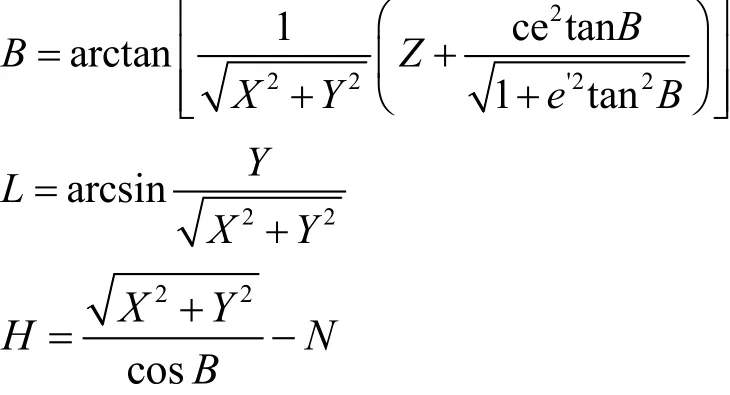
3.2 大地坐标与高斯直角坐标的转换

地面任意一点P的位置，可用高斯直角坐标表示为（x，y）。大地坐标与高斯坐标的换算关系如下：

式中，X为赤道至纬度B的子午线弧长，为计算点P与中央子午线的经差。

L－L0若以度为单位，则ρ=57.295779513；N为椭球的卯酉圆曲率半径，t=tanB，η=e’cosB，称作第二偏心率；称作极曲率半径；L0为中央子午线经度。

如果需要将高斯直角坐标换算成大地坐标，可采用如下计算方法：

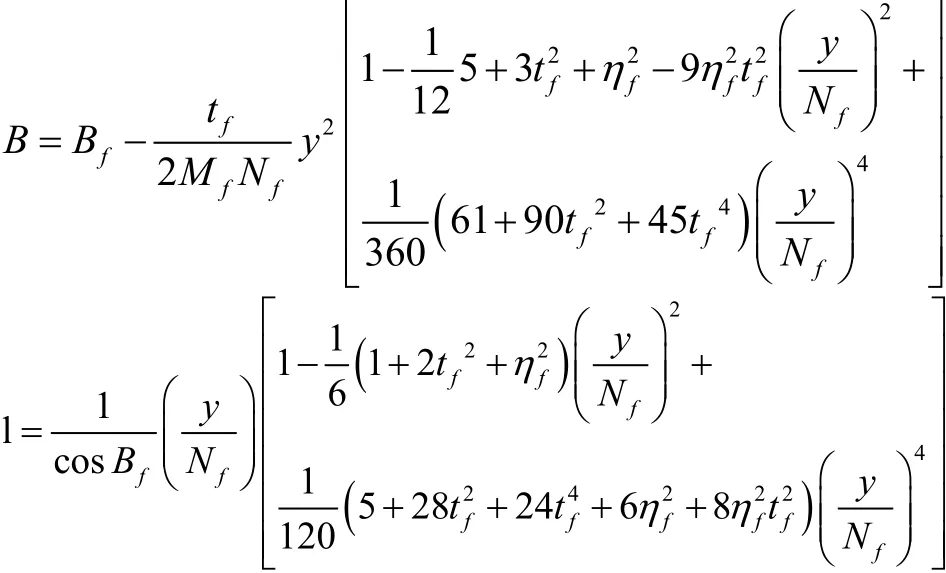
式中，Bf为底点纬度，以度为单位。由子午线弧长计算公式反算求得。其余参数计算方法与大地坐标换算高斯坐标的方法相同。

4 结语

本文对不同坐标系进行了分析，并且列举出不同坐标系间的转换模型，解决了卫星定位中位置信息的坐标系与实际需求不一致之间的矛盾，有利于卫星定位模块的广泛推广。

[参考文献]

[1]杨俊，武奇生.GPS基于原理及其Matlab仿真[M].西安：西安电子科技大学出版社，2008.

[2]贺英奎，罗强.GPS测量技术[M].重庆：重庆大学出版社，2010.

[3]宁津生.现代大地测量理论与技术[M].武汉：武汉大学出版社，2006.