基于新课程背景下初中生几何直观能力的培养
王 祎
(北京市上地实验学校)
几何直观能力就是根据当前所看到的东西进行思考、分析、总结。简单来讲,几何直观就是将复杂的数学问题通过图形方式简单化,并通过对图形进行科学分析,发现问题的实质,培养学生的逻辑分析能力。那么,基于新课改背景下,如何提升初中学生的几何直观能力?我认为需要从以下几方面研究。
一、利用数形结合方式提升学生的几何直观能力
华罗庚曾经说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。”由此可见,数和形是数学教学中非常重要组成部分,要想更好地了解数学,学懂数学,就离不开与图形的结合。所以,在对学生几何直观能力培养过程中,应该特别注重对图形语言的分析,让学生学会在答题过程中运用图形来进行解答,将代数问题与几何问题巧妙结合起来,充分将几何直观能力贯彻到代数的学习过程中。
这道题从题目上来看比较复杂,仅仅是已知正实数X,学生往往不知道如何下手,这个时候,我们不妨换个思路来思考,采用数形结合的方式进行解答。
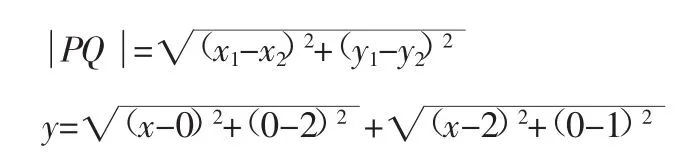
用对称轴求最短距离的方式来进行计算,通过对图形的分析和利用,问题迎刃而解。
二、通过对知识点大胆设疑提升学生的几何直观能力
在数学教学过程中,确保学生能够正确掌握、运用基础知识,大胆对问题假设,进行合理设疑,从而强化学生的创造性思维能力。例如在进行下列题目解答过程中,就可以充分运用设疑求证的思维模式进行问题解答。
如图所示,在△ABC中,∠BAC的平分线与∠ABC的平分线相较于E点,D为AE延长线与△ABC外接圆的交点,连接CE、CD、BD,已知∠CDB=120°,∠CDA=60°。试分析四边形BECD的形状。

通过肉眼观察图1,我们可以假设四边形BECD为菱形,如何证明这一假设,就需要从菱形的定义出发,证明四边形BECD的其中一组相邻边平行或者是四边都相等。
解答:因为∠CDB=120°,∠CDA=60°,根据圆周角定理可知半圆角CAB和CDB分别为240°和120°。因为四边形ACDB为圆的内接四边形,又因为∠CDB=120°,所以∠CAB=60°。因为AD为∠CAB的角平分线,所以,∠CAD=∠BAD=30°,半圆角BD=CD,所以BD=CD,又因为∠DCB=∠CAD=30°,BE是∠CBA的角平分线,所以,∠DBE=60°。同理可证∠DCE=60°。根据两组对角分别相等的四边形是平行四边形,可判定四边形BECD为平行四边形,又因为BD=CD,所以四边形BECD为菱形。
通过这种大胆设疑的方式,从方向思维来提出例证,培养学生的几何直观能力;利用基础知识大胆假设,小心求证的过程,有利于培养学生严谨的数学探索精神。
三、巧妙利用多媒体技术提升学生的几何直观能力
随着科技的不断创新,多媒体技术已经被广泛运用于教育领域,因此,在初中数学课堂教学中,教师可以巧妙利用多媒体技术,结合多媒体直观、形象、图文并茂的特点,制作具有直观性的教学课件,将枯燥抽象的数学知识形象生动化,拓展学生的思维创作能力,开拓学生视野,从而激发学生的学习兴趣,通过自主学习方式,不断培养自己的几何直观能力。但是值得我们教育工作者注意的是,多媒体技术仅仅是一种辅助的教学方式,教师不能完全依赖它,教学工作终究还是要回归课本内容。
总而言之,初中生正处于智力高速发展的重要阶段,虽然对于几何知识的学习才刚刚起步,但是,初中生的理解认知能力也正处于特别敏感的时期,因此教师在日常的教学活动中要采取有效的方法来培养学生的几何直观能力,使学生形成良好的图形感知能力。当然,这需要我们教育工作者在实践工作中不断探索,促进学生几何直观能力的有效发展。
参考文献:
魏珂,胡典顺.从一道几何题的求解浅谈几何直观能力的培养[J].中国数学教育,2017(Z3):44-46.

