图说因式分解

◎孙长江

我们知道整式的乘法与因式分解是互逆的.在学习整式的乘法时可以通过计算图形面积的方法进行推导，那么我们是否可以利用拼图的方法进行因式分解呢？下面我们一起通过几个拼图活动来试一试吧.

活动一，如图1，用若干块边长为a的正方形、边长为b的正方形、长为a宽为b的长方形纸片拼出一个图形，通过这个图形来证明因式分解的完全平方公式.

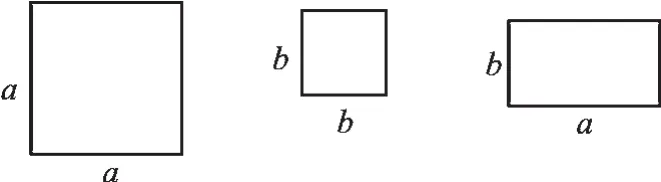
图1

通过拼图可以得到如图2的正方形.这个正方形的面积可以表示为a2+2ab+b2，也可以表示为（a+b）2.

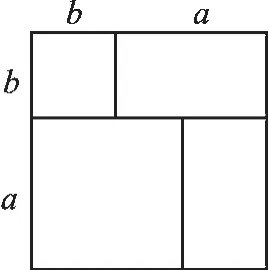
图2

于是，可以得到（a+b）2=a2+2ab+b2.

证明：a2+2ab+b2=a2+ab+b2+ab

=a（a+b）+b（b+a）

=（a+b）（a+b）=（a+b）2.

活动目的：我们可以借助于这个拼接纸片的活动，经历完全平方公式产生的过程，并进行算理的证明.

活动二，如图3，用若干块边长为a的正方形、边长为b的正方形纸片拼出一个图形，通过这个图形来证明因式分解的平方差公式.

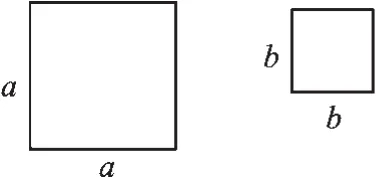
图3

通过拼图可以得到如图4的两个图形.其中，左侧图形阴影部分的面积可以表示为a2-b2.将该阴影部分裁剪、拼接后，得到右侧的长方形，其面积也可以表示为（a+b）（a-b）.

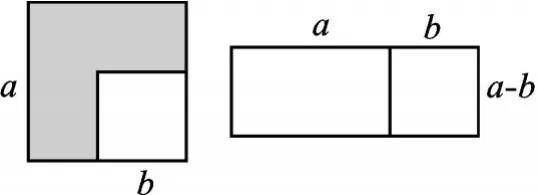
图4

于是，可以得到（a+b）（a-b）=a2-b2.

证明：a2-b2=a2+ab-ab-b2

=a（a+b）-b（a+b）

=（a+b）（a-b）.

活动目的：这个活动通过图形的叠合、裁剪、拼接等方式“玩”纸片.我们在玩中体验、感悟、理解平方差公式法因式分解的来龙去脉，并进行了算理的证明.

活动三，如图5，用若干块边长为a的正方形、边长为b的正方形、长为a宽为b的小长方形纸片拼出一个长方形，通过这个图形来证明因式分解的结果是多项式乘多项式.

图5

通过拼图可以得到如图6的长方形.这个长方形的面积可以表示为2a2+3ab+b2，也可以表示为（a+b）（2a+b）.

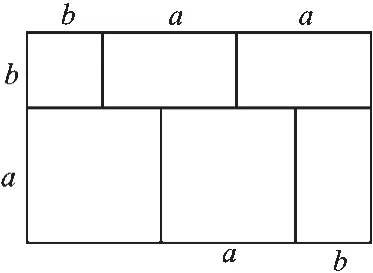
图6

于是，可以得到2a2+3ab+b2=（a+b）（2a+b）.

证明：2a2+3ab+b2=a2+2ab+b2+a2+ab

=（a+b）2+a（a+b）

=（a+b）（2a+b）.

活动目的：通过这个拼纸片的游戏感受因式分解中较难的“十字相乘法”的源起.

以上拼图活动让我们感受到了真正的“做中学”和“学中做”，帮助我们更深刻地理解了数学中的数形结合思想：拼图游戏——形；分解多项式——数.下面就让我们小试牛刀吧！

例题：有足够多的长方形和正方形的卡片，如图7.

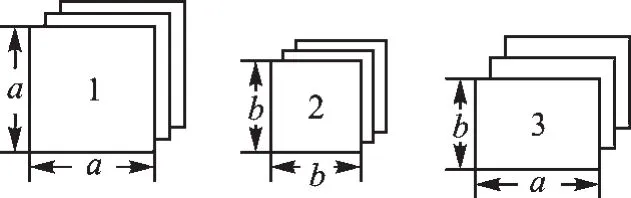
图7

如果选取的1号、2号、3号卡片分别为1张、2张、3张，如图8，可拼成一个长方形（不重叠无缝隙）.请画出这个长方形草图，并运用拼图前后面积之间的关系写出一个等式.

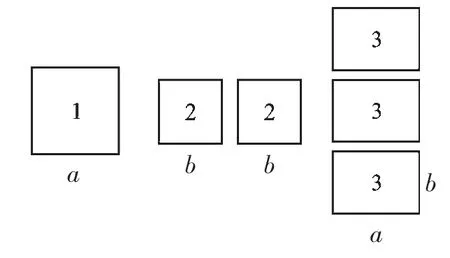
图8

这个等式是________________________.

（2）小明想用类似的方法解释因式分解2a2+7ab+3b2=（a+3b）（2a+b），那么他需要用1号纸片________张，2号纸片________张，3号纸片_______张.

【解】（1）如图9所示，我们可以拼出下面的长方形.

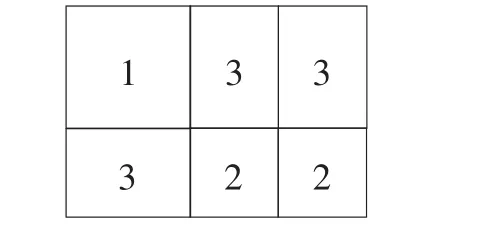
图9

这个长方形的面积可以表示为a2+3ab+2b2.

也可以表示为（a+b）（a+2b）.故，这个等式可以表示为：a2+3ab+2b2=（a+b）（a+2b）.

（2）我们也可以先进行拼图，如图10.

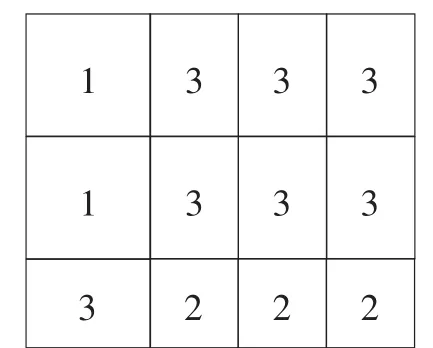
图10

通过拼图发现，这个长方形的面积可以看成是12张卡片的面积之和，即：2a2+7ab+3b2；也可以从整体来看，是一个长为a+3b，宽为2a+b的长方形，它的面积可以表示为（a+3b）（2a+b）.于是我们可以得到：2a2+7ab+3b2=（a+3b）（2a+b）.

从所拼成的长方形不难发现，需用1号卡片2张，2号卡片3张，3号卡片7张.

同学们，利用拼图对多项式进行因式分解，需要大家在活动中反复操作、尝试直至可以拼成无空隙、不重叠的长方形.经过以上尝试可以发现，通过拼图来做因式分解题费时费力，在这里不如直接用代数法来得简便、快捷.拼图法只是为了帮助大家更好地理解代数法.