算法设计与分析课程研讨教学的探索

郭惠芳，刘寒冰

（黄河科技学院 计算机科学系，河南 郑州 450063）

0 引 言

算法设计与分析课程讲授各类经典算法的基本策略和算法设计与分析的基本技巧，为学生打开了更为广阔的视野。该课程历来在专业教学中都属于高阶的、有挑战性的课程[1-2]，为此各院校就如何提高该课程教学效果与质量进行了有益的探索[3-4]。应用技术类院校培养人才的侧重点是应用型人才，算法设计与分析课程对于培养学生分析、解决问题的能力，提高学生实际编程技能有重要的作用。然而课程抽象理论偏多，相当一部分学生的基础知识不够扎实，接受能力有限。每年课程刚开始时，学生对算法设计有较浓的兴趣，这个从他们热切的眼神中可以看出来，但随着课程的推进，部分学生遇到了一些困难，学习参与度降低，课堂效率降低。

1 研讨课的设想

为了改善算法设计与分析课程的教学效果，希望通过研讨课的模式，在教学过程中启发学生研究和探索的兴趣，培养学生发现问题、提出问题、解决问题的意识和能力。首先引导学生在课下进行自“研”：充分利用老师提供的及网上的学习资源，就布置的专题查阅资料，研究其内在原理和过程。然后在课上的“讨”：汇报研究的内容，并将研究过程中遇到的问题提出来讨论。我们为该课程设计了1个课外开放专题、4个课内专题，课前2周布置。

1.1 课外开放专题

基于前序数据结构课程的学习，引导学生了解算法在各行各业中的运用，如大数据挖掘中的算法、导航系统中的算法等。督促学生查阅在各个应用领域得到较好应用的算法，通过查找相关资料，引导大家了解算法应用的不同业务领域，并写出报告，在研讨课中进行汇报与讨论。

1.2 课内专题

课内专题是在教材[5]的每类算法中选择一个问题进行讨论。

（1）分治法中选择了快速排序，要求课下通过阅读相关材料，给出快排中划分方法的几种实现，讨论使用尾元素作为划分基准的方法。

（2）动态规划方法中选择了最大子段和的求解，要求课下阅读相关材料，分别给出穷举法、分治法以及动态规划方法的实现，讨论3种方法的时间复杂度，体会相同问题的不同算法效率的差别。

（3）贪心算法中选择了贪心算法适用性的讨论，以0-1背包和背包问题为案例，说明贪心算法的适用性，同时讨论找零钱问题的贪心算法的适用性。

（4）回溯法和分支限界法选择了迷宫问题进行讨论，要求分别给出迷宫问题的回溯法（以深度优先搜索顺序）以及分支限界法（以广度优先搜索顺序/最优目标值优先顺序）的求解方法，并给出搜索轨迹，讨论两种方法的联系及区别。

通过课下研究、课上讨论，引导学生独立思考，深入理解相关内容，逐步掌握经典算法的设计技巧，提高代码编写的能力，同时不断树立学习的自信心，提高自主学习的能力。

2 研讨课的实施

2.1 课外专题研讨的困境

研讨题目和要求布置一周后，发现学生课下研究的主动性不高，询问后得知，独立自主地选择一个主题、查资料进行研究对于他们还有些陌生。经过在线的跟踪指导，学生上报了一些好的选题，例如，百度云秒传功能的实现——浅谈Hash算法、网易云音乐的推荐算法、地图中最短路径的搜索算法研究、遗传算法、数独算法、卫星导航定位系统等。

在随后的专题研究中，大部分学生有等、靠、拖的思想，部分学生研究、思考浮于表面，上交的汇报很大程度上是从网上摘抄下来且没有自己的理解与思考的内容。在老师的持续督促及指导下，一部分学生查询与消化相关专题的资料，课下进行了较为细致的研究，共有5组学生进行了课上汇报。课外专题汇报过程中，台下的学生虽然有一定的兴趣，但极少发言，大部分学生未能真正进入讨论状态，主要原因是台下学生很难明白台上讲的内容，课外专题的研讨未能达到预期状态。

2.2 化整为零的课内专题研讨

课外专题研讨的冷场说明，研讨环节中的“研”完全依赖学生课下进行自主地学习与研究是有一定困难的，就一个完整问题进行研究，学生畏难情绪重，自学能力偏弱。仅仅开展形式上的研讨教学，并不能达到预期，研讨的内容必须根据不同的教学对象进行相应调整，于是我们将每个算法问题化整为零，降低研究难度，将部分完整专题分解为局部问题的讨论。

1）快速排序。

我们将研讨题目细分为4个子题目：①利用一个划分实例演示以首元素为基准进行划分的过程；②在前者基础上，i、j指针轮流进行扫描后进行交换以及i、j扫描后即进行元素的移动，两种方式分别进行演示；③以尾元素进行划分基准，以实例演示划分过程；④实例演示后，对照过程实现该过程的程序代码。

分解后的每个子题目分配给一位学生准备，课上进行演示，由于难度降低，学生完成度高，其余学生对相应问题都有一定的知识基础，学生在台上的每个演示动作可能都反映了台下部分学生的思路，学生容易进入状态，上台同学积极思考，台下同学积极讨论，遇到困难时，学生就自告奋勇地上台来进行纠正，讨论气氛完全达到了预期效果。参与度的提高带来的是学习热情的高涨。

2）贪心算法。

专题分为3个子题目：①背包问题的贪心算法实例演示；②0-1背包问题贪心法的失败实例演示；③找零钱的贪心算法成功与失败的实例演示。

该专题的子题目难度较低，学生参与度比较高，学生研究、讨论得非常成功，在总结讨论为何背包问题可以用贪心法求解，而0-1背包问题不一定能用贪心法得到最优解时，大部分学生都能比较清晰地回答其关键所在。

3）迷宫问题。

被分解为3个子问题：①深度优先的回溯解法；②广度优先的分支限界法；③针对后者的优化手段有哪些？

学生对该问题表现了很大的兴趣，前两个学生分别演示了自己实现的程序，界面各有特色，并显示了访问路线，直观地让同学们看到了两种方法的区别，优劣一目了然。准备优化方法的学生虽然没有讲到重点上，但是在老师的提示下，台下的学生最终提出了比较好的优化方法。经过这个专题的研讨，学生对回溯法与分支限界法有了比较直观的理解，增加了解决问题的自信心。在课堂讨论过程中，涌现了一些有想法、有探索欲望的学生，还有一些学生展示了良好的表达能力，这些学生课下能够主动与老师在线讨论、交流课外学习的内容，研讨的氛围逐步建立。

2.3 实验环节的自发研讨

以往在实验课前，老师将上机题目布置下去，上机时由老师在实验室辅导答疑，最后学生上交实验报告，老师据此打分。这个过程中部分学生学习不够认真、抄袭现象频发；还有一部分学生想独立完成，但遇到问题没有勇气请老师来帮助，最终放弃。

将“研讨”精神引入实验室，激发学生想学习的潜在欲望。首先要求抽签决定上机题目，老师贴近学生，及时发现学生的学习状态，主动询问引导，鼓励他们相互讨论和帮助。老师对每位学生实施一对一答辩，再据此打分。这一点对学生促动很大，在实验环节中自发地形成小组，进行讨论，相互研讨、学习的气氛因而显现。

打分是在答辩后进行，学生如果希望得到一个高分，就必须平时多下工夫，在老师面前有一个好的表现，如：为了搞清一个问题，常有学生中午在实验室加班调程序，也有学生自己感觉分数低，经过持续的努力，要求老师再次考核，这些现象都令老师感到欣慰，没有比学生自己想要学更好的学习方法了。

3 课程考核

考核是检验教学方法优劣和督促学习的一种有效手段。本次课程考核分为平时考核、实验考核以及期末考核。实验考核方法上面已有阐述，平时考核中增加了课堂测试环节。

3.1 课堂的测试环节

课内研讨的气氛调动了大部分同学的积极性，但为了防止部分同学只看热闹，学习中不求甚解、浮于表面，在课堂上增加了测试环节，学生平时课堂的测试参与度及测试成绩作为平时考核的一部分，计入课程最终考核。我们已在移动互联网上提供课堂测试功能，有200道左右题目可供测试，在课堂上学生利用手机进行回答，老师可以快速了解学生每个阶段的知识掌握情况。课堂上增加过程检查环节，督促和帮助学生及时进行复习，同时促进学生独立地完成作业。

3.2 期末考核

计算机科学专业班没有进行研讨课的试点，但是在课堂上对大部分的算法实例都采用研讨式的讲法，只是未进行课外专题的研究和讨论，同时也增加了课堂测试环节。全班人数30人，期末考核平均分为80.3，总分分布如图1虚线所示。相比前二届（前后试卷难度相当）的成绩（78分左右）有明显提高。

软件工程专业是研讨课试点班，全班共45人，平均分81.4，总分的分布情况如图1实线所示，成绩相比前二届的学生成绩有较大提高，横向比较，相比计算机科学专业班的成绩也有些优势。软件工程专业出现一个99分最高分，90分以上有9人，这部分学生知识掌握得很好，失分基本是由个别的填空或问答题的回答不准确造成的。80分以上有18人，这部分学生对知识的掌握基本达到预期，在分析和设计题中有少量失分，基本概念部分（问答题或填空题）掌握较好。

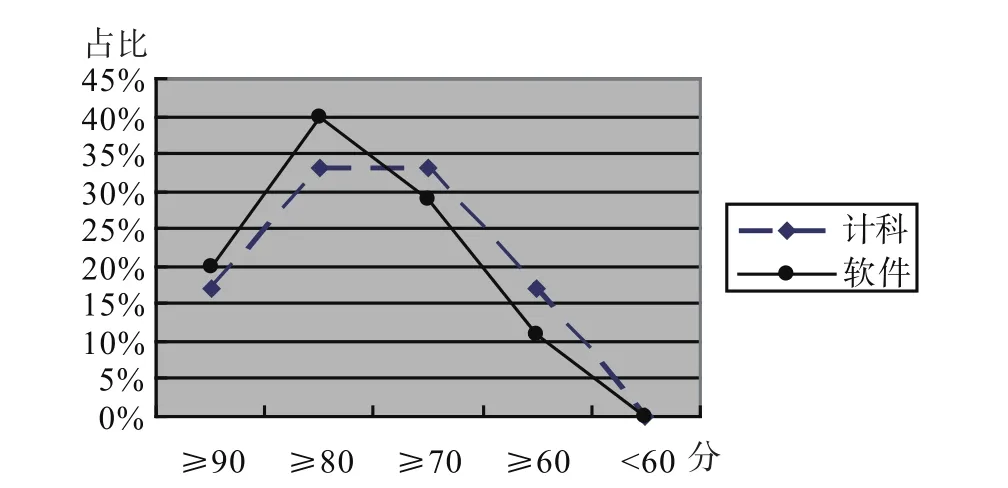
图1 计算机专业与软件专业期末卷面分分布图

4 结 语

从课内专题研讨的情况看，本次研讨课的开展在提高学生学习兴趣和学习参与度方面有明显效果；期末考试中极低分数明显减少，同时80分以上同学的占比显著提高，这些都说明，在实验环节营造研讨氛围、在课堂测试环节保证学习热情持久性等措施对于提高学习成绩是有效果的。

培养应用型人才，首要的是树立学生的自信心和鼓励学生探索的勇气，这是培养任何能力和素养的前提，研讨课的开展也必须遵循这个前提。要取得良好的教学效果，研讨教学的形式不是最重要的，重要的是以下3个关键点：①内容大于形式，研讨课的内容组织要能真正调动大部分学生的积极性；②态度决定成败，贯彻教学始终的研讨态度与习惯要能挖掘出学生潜在的学习欲望；③过程控制是保障，从每个教学环节督促与检查是研讨课取得成绩的必要条件。本次研讨课虽然取得了一些成绩，但教学本身就是一个不断研究与讨论的过程，教学研讨抑或是研讨教学都将继续进行，因为研讨本就是一种工作、学习态度，作为教师，我们要传递的就是，知识绝不仅仅是老师说的、书上写的，更多的要通过自己的探究与检验才能得到。

参考文献：

[1]陈翔. 面向算法设计与分析课程的翻转课堂教学模式研究[J]. 计算机教育, 2016(8): 147-151.

[2]李志欣. 算法设计与分析课程的教学探索与实践[J]. 教育教学论坛, 2013(13): 218-219.

[3]秦董洪, 陈智勇. 算法设计与分析课程教学研究[J]. 计算机教育, 2013(11): 98-101.

[4]林劼, 戴波. 项目驱动型算法设计与分析课程教学方法[J]. 计算机教育, 2014(9): 69-71.

[5]王晓东. 计算机算法设计与分析[M]. 4版. 北京: 电子工业出版社, 2012: 20-22.