超声速边界层转捩预测eN方法及其软件开发
黄章峰, 肖凌
(1.天津大学 力学系, 天津 300072; 2.空气动力学国家重点实验室, 四川 绵阳 621000)
0 引 言
空气动力学研究是航空航天技术发展的必要条件。高速飞行的一系列具有挑战性气动问题之一就是边界层转捩位置的预测[1]。由于湍流的摩擦系数和传热系数远大于层流,边界层是否转捩和在何处转捩直接影响飞行器的摩擦阻力、热防护及流动分离位置等[2-3]。若能较准确地预测出转捩位置并延迟转捩的发生,则可以提高升阻比预示精度,降低燃料消耗,为热防护设计提供依据,大大地改进飞行器性能。因此,边界层转捩预测对于大飞机,尤其是对超声速、高超声速飞行器的研制,是至关重要的,得到了航空航天设计研发部门的高度重视[4]。
随着计算机性能的提高,计算流体力学(简称CFD)已经成为飞行器设计的重要研制手段。精确给出升力、阻力及热流分布等重要参数的前提之一是准确预测飞行器边界层的转捩位置。研发单位采用CFD计算气动力、热时,转捩位置往往是人为给定的,导致计算结果偏差较大。目前许多新一代航空航天飞行器的研制已提上日程,降低阻力、减少热流、提高升阻比、改进气动性能成为迫切需要解决的问题。因此研发单位迫切需要实用、简便的转捩预测软件。
1 国内外研究现状
目前主要的转捩预测方法有三类:1) 转捩工程判据[5-6]:在航空界应用较普遍,主要依赖于实验结果和经验,定义某种雷诺数作为转捩工程判据。对于不可压缩流动,流动参数只有雷诺数,且实验较多,转捩工程判据比较适合。对于可压缩流动,流动参数较多,如马赫数、来流温度和壁面温度等,且实验比较昂贵,因此转捩工程判据的建立相对比较困难。2) 层流-湍流转捩模式[7-8]:与湍流模式类似,引入间歇因子,建立间歇因子的模式方程,在计算流场的过程中根据间歇因子预测转捩。在间歇因子模式方程中有较多的非普适参数,限于对转捩机理的认识和实验的匮乏,这些参数很难校准,因此不能有效地解决转捩预测问题。3) eN方法[9]:是基于科学问题研究的转捩预测方法,该方法尽可能多地利用了边界层中扰动演化的理论预测。其理论基础是线性稳定性理论(简称LST)[10]。在高空飞行的飞行器,来流中的扰动为小扰动,在大部分区域,扰动演化可以用LST描述。该方法在航空界取到了很好的效果[11],波音公司的资深工程师Cebeci称,迄今为止,最有效的转捩预测方法仍是eN方法[12]。
鉴于eN方法的优势,国内外学者已将该方法应用到工程实践中,编制了转捩预测软件,主要有两大类:
一类是以Malik为代表的eN转捩预测方法,该类方法可用于低速及高速边界层。美国宇航局(简称NASA)的Malik等[13]基于eN方法开发了转捩预测软件 (称为eMalik),并发展了一系列的工具包(简称GTPT)[14],在工程转捩预测中起了重要作用。美国NASA的Chang[15]基于线性稳定性理论、抛物化稳定性方程和eN方法开发了一套流动稳定性分析和转捩预测的代码(称为LASTRAC),并在HIFiRE5模型[16]上成功应用。比利时的Fabio[17]开发了边界层稳定性分析和转捩预测的软件工具包(称为VESTA toolkit)。结合转捩预测eN方法和RANS求解器,俄罗斯的Boiko等人[18]将层流-湍流的转捩预测模块添加到LOGOS软件中,并在平板和后掠翼[19]上成功应用。西北工业大学的宋文萍等[20]将eN方法嵌入到RANS方程中进行耦合求解,并成功应用于两种亚声速翼型的转捩位置预测和气动特性仿真。天津大学团队编写的转捩预测程序,成功对平板[21]、钝锥[22]、后掠翼[23]等流动进行了转捩预测,经过初步集成,可以在工程单位对复杂三维边界层进行转捩预测。
另一类是以Arnal为代表的eN-Database转捩预测方法,该类方法只适合低速边界层。法国国家航天航空研究中心(简称ONERA)的Arnal等[24]根据低速平板边界层中基本流相似的特点,建立了一套转捩预测方法(称为eN-Database),并嵌入到ONERA开发的elsA软件中,在给定转捩判据的条件下,实现了转捩位置自动预测[25]。德国宇航中心(简称DLR)的Krumbein[26]将该方法嵌入到DLR开发的结构网格求解器FLOWer[27]和非结构混合网格的求解器TAU[28]中,实现了转捩预测和流场的同时计算。最近他们基于不同的流线方法对转捩预测技术进行了改进,并取得了很好的效果[29]。瑞典国防研究局(简称FOI)的Eliasson等[30]将该方法添加到FOI开发的基于非结构混合网格的求解器 Edge 中,在高升力构型的应用中取得了很好的结果。中航工业空气动力研究院的董军等[31]将该方法耦合到自行开发的非结构混合网格求解器(简称UNSMA)中,实现了对转捩点位置的判断,提高了对三维机翼等构型的阻力预测精度。
2 现有转捩预测的不足
近些年由于国家的重视,我国在转捩预测基础理论的研究已经达到国际先进水平,并初步具有工程应用的能力,然而在向工程应用推广方面还存在明显的不足,很多方面有待于提高。
从理论方面讲,eN方法仍然存在一些可以进一步完善的地方。
1) 没有考虑感受性问题: eN方法中积分增长率是从扰动的中性位置开始的,而且假设积分起始位置的扰动幅值相同,没有考虑来流中扰动幅值随频率的变化。实验结果表明,转捩位置会随着来流湍流度的增大而明显提前。因此需要研究来流扰动激发边界层内的不稳定波的机理,确定转捩与来流扰动幅值之间的定量关系,为转捩位置的预测提供扰动演化的上游条件。Saric[32]、Fedorov[33]、Zhong[34]等总结了边界层感受性问题的理论、计算和实验进展。天津大学团队[4]总结了外来扰动激发不稳定模态的机理,并对eN方法进行了改进[35],与King[36]的实验结果和李新亮等[37]的DNS结果相符。
2) 忽略了非平行性影响:LST是基于局部平行流假设,而非平行性对于有些流动的影响可能较大[38]。Gaster[39]、Betolotti等[40]、唐登斌等[41]研究了非平行性对流动稳定性的影响。抛物化稳定性方程(简称PSE)[42]是当前常用的考虑非平行性的数值方法,在不可压缩流中得到了很好的应用。但PSE的方程是抛物型的,需要推进求解,工程应用不方便[43]。天津大学团队[44]提出了一种考虑基本流和特征函数沿流向方向变化的扩展特征值方法(简称EEVn),可以考虑阶数为n的高精度情况。n=1为阶数最小的常用方法,称为抛物化稳定性方程的展开解(简称EPSE)[45]。该方法仍是一个特征值问题,可以替代LST。
3) 三维边界层中更合理的波数确定方法:LST只能提供一个求解波数的关系,而在三维边界层中有两个方向的波数。如何补充另一个波数的关系式是三维边界层中转捩预测的关键问题。Cebeci等[46]利用鞍点法给出了补充的关系式,但需要迭代求解,工作量大。针对三维性较弱的边界层,Malik等[47]建议取势流方向的横向波数为实数,并沿着势流方向进行积分,该方法的计算量和误差均很小,对工程计算来说是一个很好的近似。针对三维性较强的边界层,天津大学团队[48]提出了等效展向波数法,取得了很好的效果。
4) 转捩判据依赖实际飞行情况:eN方法中转捩判据主要依靠实验或经验来确定,对于超声速飞行器,这方面的经验还很少[33]。美国启动了国家航天飞机项目(简称NASP),对边界层转捩进行了大量的CFD仿真、风洞实验和飞行试验,建立了两组外形的超声速边界层转捩数据库,取得了重大进展[49]。欧洲也设有专门的重大研究计划,通过大量的实验确定转捩判据。天津大学团队对不可压缩的槽道流[50]、超声速、高超声速平板[51-52]和锥体[53]做过很多转捩的数值模拟,建议将通过LST得到的小扰动幅值增长到1.5%来作为转捩开始的判据,并对eN方法进行了改进[54],取得了很好的结果。
从工程应用方面讲,现有的基于eN方法的转捩预测软件也存在一些问题。
1) 未包含感受性、转捩机理等新的理论成果;
2) 通用性较差,尤其对是三维性较强的飞行器;
3) 效率较低,距研发单位的需求还有差距。以两千万的网格量(流向500×法向200×展向200)计算,壁面上(流向×展向)有十万个网格点,即使在每个网格点上花1秒钟时间完成全部稳定性分析,完成全部区域的转捩预测时间也是以天为单位计算。对于简单流场剖面,基本上在这1秒钟完成谱空间(频率、展向波数)上近1000个工况(频率个数50×展向波数个数20)的流向波数估算等稳定性分析,但对复杂一些的剖面,时间可能需要花费10 s,导致工程单位进行转捩预测的时间有时需要以周为单位,远远不能满足研发单位的需要。
4) 需要大量的人工干预,如基本流处理、特征值初值估计、非物理解判断、转捩位置评估等,对操作人员的专业水平要求高。
3 发展动态分析
随着超声速飞行器的发展,转捩预测的发展呈以下三大趋势:
1) 将更多的理论研究成果用于转捩预测方法,如感受性及转捩机理等。边界层内扰动初始幅值与来流扰动的能谱紧密相关,来流扰动直接影响转捩位置。转捩判据的物理本质是转捩机理的问题。一个完善的转捩预测方法,应该能将感受性、结合转捩机理的转捩判据都考虑进去,使转捩预测方法更理性化,从而尽量减少对实验和经验的依赖。这对我国来说尤为重要,因为我们的起步晚、基础弱,缺乏必要的实验和经验,而实验既难做又耗资巨大。
2) 面向超声速、高超声速流动。超声速、高超声速飞行器是航空航天的发展方向。超声速与亚声速流动存在明显的不同,给转捩预测带来新的挑战。对于亚声速流动,边界层外的扰动需要间接地激发边界层内的不稳定波,而且同一个位置上仅存在一个模态的不稳定波;对于超声速流动,边界层外的扰动可以直接和间接激发边界层内不稳定波,同一个位置上存在多重模态,而且不同模态之间可能发生合并或转换现象。要正确预测超声速流动的转捩位置,需要考虑超声速对感受性、扰动演化和转捩机理的影响。
3) 转捩预测要面向工程,具有实用、高效、友好等特点。转捩预测软件是面向工程的,应具有实用的特点,满足不同飞行器外形的应用需求,适用于较大马赫数、雷诺数范围,具有一定的通用性;应具有高效的特点,能快速地完成转捩预测,满足飞行器外形设计的需要;应具有界面友好、易操作、自动化程度高的特点,降低对使用人员的专业水平和技术水平要求;应具有良好的对内可扩展性和对外兼容性,对内支持加入新的研究及测量结果,对外可以被工程单位常用的CFD软件调用,实现转捩位置预测和流场模拟耦合进行。
4 工程转捩预测软件的实现途径
边界层转捩精确预测是工程的需要,也是学科研究的目标[4]。从工程方面,希望用最简单的方法预测出工程要求精度范围内的转捩位置,从学科研究方面,则希望对整个转捩涉及到的问题都研究清楚,能够提出预测转捩的科学方法,但实际上,转捩预测问题的复杂性大大超出了人们的预想,甚至有的学者对高超声速边界层转捩预测持怀疑观点。仅仅依靠流动稳定性理论和传统的eN方法无法真正意义上的实现转捩预测,因为它忽略了背景扰动,仅仅考虑了扰动幅值的放大倍数。
从学科研究的角度来看,目前短时间内难以解决感受性问题,也无法完全预先了解具体背景扰动的频谱特征;但是从工程的角度来看,同一风洞或同一高度的扰动频谱特性变化不大,应该具有一定的普适性,工程上不指望完全定量给出感受性系数,但是有望较准确给出感受性系数的数量级,在建立一系列知识库的基础上,对转捩预测eN方法进行改进,结合流动稳定性分析和转捩工程应用方面的经验,有望开发一套实用、全自动、高效、用户接口友好的工程转捩预测软件。
4.1 特征值知识库的建立
基于eN-Database的思想,采用稳定性分析的方法事先求出典型边界层基本流剖面的最不稳定波的特征值;并根据基本流剖面的特征参数建立不稳定波的特征值知识库。基于机器学习方法,对知识库进行补充和更新。在求解未知基本流剖面的特征值时,首先分析基本流剖面的流动特征参数,并根据流动特征参数和无量纲的基本流剖面在知识库中查找相近剖面对应的特征值,并以该特征值作为初值,对特征参数和基本剖面进行变换,快速求得未知基本流剖面的最不稳定波的特征值。
4.2 感受性系数知识库的建立
针对边界层外缘感受性,结合已有的感受性理论,采用数值方法建立激波后扰动与激发的边界层内不稳定波的初始幅值之间的定量关系;再利用数值方法或激波关系式确定激波前后扰动的定量关系;最终确定来流扰动与被激发的边界层内不稳定波的初始幅值之间的定量关系,即感受性系数;然后对风洞或飞行工况的来流扰动能谱进行特征分析,根据飞行条件的参数建立感受性系数知识库。在已有知识库的基础上,基于机器学习方法实现学习和更新功能。在工程应用中,利用有限的数值和实验数据对知识库进行标定和修正,并不断补充和完善知识库。在转捩预测时,通过查找感受性系数知识库,获得不稳定波的初始幅值,为转捩位置的预测提供扰动演化的上游条件,实现在转捩预测中考虑感受性的因素。
4.3 转捩判据知识库的建立
在建立感受性系数知识库的基础上,采用LST找到触发转捩的扰动;结合非线性稳定性理论,适当加入非线性作用最强的其它扰动,采用非线性PSE计算到转捩;针对两种不同模态激发转捩的若干种情况进行研究,然后找出一定的规律来,确定有明确物理意义的转捩判据;然后对转捩判据进行分析、修正和归类,并根据飞行条件的参数建立转捩判据的知识库。该知识库需要在工程应用中不断补充和完善。在转捩预测时,根据飞行条件在转捩判据知识库中查找或者由用户指定转捩判据,实现转捩位置的自动预测。
4.4 全自动、高效的转捩预测软件的开发
全自动、高效的转捩预测软件主要包括四大模块,其流程图及与三个知识库的关系如图1所示。
1) 基本流处理:首先对给定的基本流数据进行网格、流场和边界条件识别,建立多块结构化网格之间的关系;然后对流动特征参数进行分析,并对基本流进行无量纲化;最后将流场从直角坐标系转换到正交的贴体坐标系下,提取出全场边界层壁面上的基本流剖面和流动特征参数。
2) 稳定性分析:首先根据正交贴体坐标系下的流动特征参数对流场进行定性分析,确定最不稳定波存在的可能位置,根据该位置处的流动特征参数和基本流剖面,在特征值知识库中查找相近的特征值作为初值;然后对每个特征值所对应的特征函数进行分析,剔除特征值问题中的数值解,实现物理解的智能识别;最后以已知位置上的特征值为初值,对该位置的邻近位置进行求解,从而求出全场各个位置上最不稳定波的特征值,进而进行中性曲线、最不稳定波的稳定性特性分析。
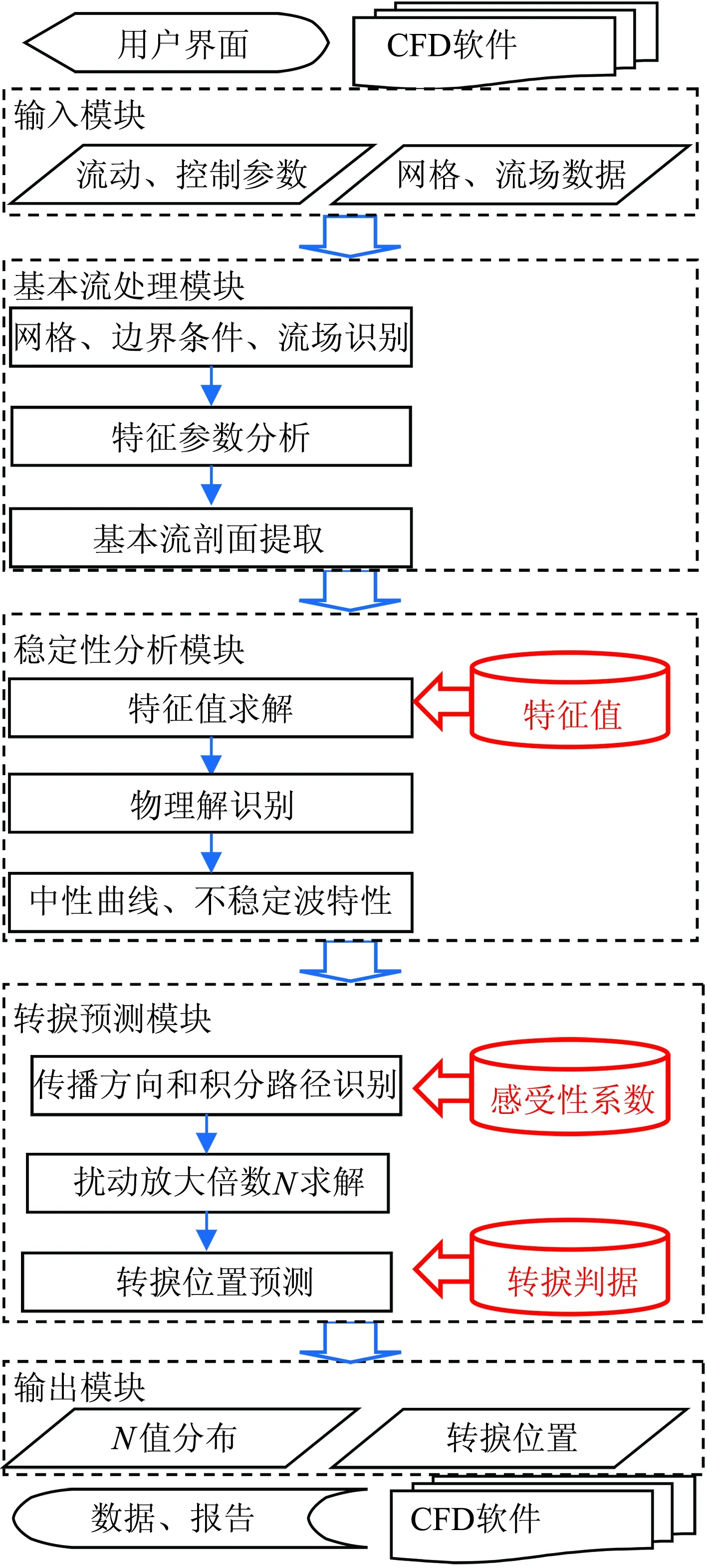
图1 软件流程图及与知识库的关系Fig.1 Flow chart of the software and its relationshipwith knowledge databases
3) 转捩预测:首先根据中性曲线确定全流场不稳定波的频率范围,根据每个位置上最不稳定波的特征值求出每个不稳定波的特征值;然后采用等效展向波数法确定每个不稳定扰动波的展向波数和传播方向,根据飞行条件在感受性系数知识库中查找和插值得到不稳定波开始增长位置的幅值,考虑感受性的影响,对增长率沿着扰动波的传播方向进行曲线积分,得到该扰动幅值A在壁面上的分布;根据飞行条件在转捩判据知识库中查找或者由用户指定转捩判据AT值,当首个扰动幅值达到AT时预测转捩开始的位置。
4) 前后处理:设计和实现用户友好的操作界面和接口。针对基于结构网格求解器的常用CFD软件,编写相应的软件接口,从CFD软件中输入飞行参数和基本流数据,向CFD软件输出转捩线的分布,以便CFD软件在转捩线的上游采用层流模型、在转捩线的下游采用湍流模型仿真,从而实现转捩预测与流场仿真的耦合计算。
5 结 论
随着超声速飞行的发展,航空航天设计研发部门迫切需求面向工程的超声速边界层转捩预测软件。经过长期不懈努力,高超声速边界层转捩的研究在理论上取得了很大的进展,但在工程应用方面还存在明显的差距。通过对现有的转捩预测方法和软件进行不足分析,从工程应用的角度出发,提出了面向工程的转捩预测软件的实现途径。在该实施过程中,需要各个部门、各个单位的协作,充分利用理论分析成果、数值仿真结果、风洞和飞行试验数据,建立相应的知识库,对转捩预测eN方法进行改进,结合工程应用经验,有望开发一套实用、全自动、高效、用户接口友好的工程转捩预测软件。
参考文献:
[1]Zhuang F G, Cui E J, Zhang H X.Some development of future spacecrafts and aerodynamics tasks[M].Beijing: National Defense Industry Press, 2006: 1-12.(in Chinese)庄逢甘, 崔尔杰, 张涵信.未来空间飞行器的某些发展和空气动力学的任务[M].北京: 国防工业出版社, 2006: 1-12.
[2]Zhang H X, Zhou H.On basic research on fluid mechanics[J].World sci-tech R&D.2001, 23(1): 15-18.(in Chinese)张涵信, 周恒.流体力学的基础研究[J].世界科技研究与发展, 2001, 23(1): 15-18.
[3]Zhou H.Requirements for fluid mechanics in the new century[J].Progress in Natural Science, 2000, 10(6): 491-494.(in Chinese)周恒.新世纪对流体力学提出的要求[J].自然科学进展, 2000, 10(6): 491-494.
[4]Luo J S.Transition and prediction for hypersonic boundary layers[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357-372.(in Chinese)罗纪生, 高超声速边界层的转捩及预测[J].航空学报, 2015, 36(1): 357-372.
[5]Kong W X, Zhang H, Yan C.Transition criterion prediction method for hypersonic boundary layer[J].Missiles and Space Vehicles, 2013, 328: 54-58.(in Chinese)孔维萱, 张辉, 阎超.适用于高超声速边界层的转捩准则预测方法[J].导弹与航天运载技术, 2013, 328: 54-58.
[6]Zhou L, Yan C, et al.Transition model and transition criteria for hypersonic boundary layer flow[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1092-1102.(in Chinese)周玲, 阎超, 等.转捩模式与转捩准则预测高超声速边界层流动[J].航空学报, 2016, 37(4): 1092-1102.
[7]Fu S, Wang L.Progress in turbulence/transition modelling[J].Advances in Mechanics, 2007, 37(3): 409-416.(in Chinese)符松, 王亮.湍流转捩模式研究进展[J].力学进展, 2007, 37(3): 409-416.
[8]Zhang W, Liu P Q, et al.Review of transition prediction methods[J].Journal of Experiments in Fluid Mechanics, 2014, 28(6): 1-12.(in Chinese)张雯, 刘沛清, 等.湍流转捩工程预报方法研究进展综述[J].实验流体力学, 2014, 28(6): 1-12.
[9]Saric W S.Physical description of boundary layer transition, experimental evidence[R].AGARD-CP-793, 1994.
[10]Mack L M.Boundary-layer linear stability theory[M].NASA, International Organization, 1984.
[11]Zhang D M, Luo J S, Zhou H.Dynamic model of coherent structure in the wall region of a turbulent boundary layer[J].Science in China series G, Physics Astronomy, 2003, 46(3): 291-299.
[12]Cebeci T, Shao J P, Chen H H, et al.The preferred approach for calculating transition by stability theory[R].An Inter-national Conference on Boundary and Interior Layers, July 5-7, 2004.
[13]Malik M R, Zang T, Bushnell D.Boundary layer transition in hypersonic flows.AIAA-90-5232[R].Reston: AIAA, 1990.
[14]Malik M R.Boundary-layer transition prediction toolkit.AIAA-97-1904[R].Reston: AIAA, 1997.
[15]Chang C L.Langley stability and transition analysis code (LASTRAC) version 1.2 user manual[R].NASA TM-2004-2133233, 2004.
[16]Choudhari M, Chang C L, Jentink T, et al.Transition analysis for the HIFiRE-5 vehicle.AIAA 2009-4056[R].Reston: AIAA, 2009.
[17]Fabio P.VESTA toolkit: a software to compute transition and stability of boundary layers.AIAA 2013-2616[R].Reston: AIAA, 2013.
[18]Boiko A V, Nechepurenko Y M, Zhchkov R N, et al.Laminar-turbulent transition prediction module for LOGOS package[J].Thermophysics and Aeromechanics, 2014, 21(2):191-210.
[19]Boiko A V, Nechepurenko Y M, Abalakin I V, et al.Numerical prediction of laminar-tubulent transition on an airfoil[J].Russian Journal of Numerical Analysis and Mathematical Modelling, 2014, 39(4): 205-218.
[20]Zhang K, Song W P.Application of the full eNtransition prediction method to aerodynamic characteristics calculation of accurate airfoils[J].Journal of Northwestern Polytechnical University, 2009, 27(3): 294-299.(in Chinese)张坤, 宋文萍.基于线性稳定性分析的eN方法在准确预测翼型气动特性中的应用[J].西北工业大学学报, 2009, 27(3): 294-299.
[21]Cao W.A study of the transition prediction of hypersonic boundary layer on plane and wedge flow[J].Acta Aerodynamica Sinica, 2009, 27(5): 516-523.(in Chinese)曹伟.高超声速边界层的转捩问题[J].空气动力学学报, 2009, 27(5):516-523.
[22]Su C H, Zhou H.Stability analysis and transition prediction of hypersonic boundary layer over a blunt cone with small nose bluntness at zero angle of attack[J].Applied Mathematics and Mechanics-English Edition, 2007, 28(5): 563-572.
[23]Huang Z F, Lu X Z, Yu G T.Cross-flow instability analysis and transition prediction of airfoil boundary layer[J].Acta Aerodynamica Sinica, 2014, 32(1):14-20.(in Chinese)黄章峰, 逯学志, 于高通.机翼边界层的横流稳定性分析和转捩预测[J].空气动力学学报, 2014, 32(1): 14-20.
[24]Arnal D, Casalis G.Laminar-turbulent transition prediction in three-dimensional flows[J].Progress in Aerospace Sciences, 2000, 36:173-191.
[25]Perraud J, Arnal D, Casalis G, et al.Automatic transition prediction on using simplified methods.AIAA 2009-1144[R].Reston: AIAA, 2009.
[26]Krumbein A.eNtransition prediction for 3D wing configurations using database methods and a local, linear stability code[J].Erospace Science & Technology, 2008, 12(8): 592-598.
[27]Krumbein A.Automatic transition prediction and application to 3D wing configuration[J].Journal of Aircraft, 2007, 44(1): 119-133.
[28]Krumbein A, Krimmelbein N.Automatic transition prediction for three-dimensional configurations with focus on industrial application.AIAA 2010-4292[R].Reston: AIAA, 2010.
[29]Krumbein A, Krimmelbein N, Grabe C.Streamline-based transition prediction techniques in an unstructured computational fluid dynamics code[J].AIAA, Journal, 2017, 55(5): 1548-1564.
[30]Eliasson P, Hanifi A, Peng S H.Influence of transition on high lift prediction for the NASA trap wing model.AIAA 2011-3009[R].Reston: AIAA, 2011.
[31]Dong J, Gao D F, Ren Y G, et al.Coupling and application of eN-database method to transition prediction in a 3D unstructured solver[J].Journal of Shenyang Aerospace ace University, 2015, 32(2): 11-17.(in Chinese)董军, 高德峰, 任园军, 等.eN-Database转捩预测方法在三维非结构求解器中的耦合与应用[J].沈阳航空航天大学学报, 2015, 32(2):11-17.
[32]Saric W S, Reed H L, Kerschen E J.Boundary-layer receptivity to freestream disturbances[J].Annu.Rev.Fluid Mech, 2002, 34: 291-319.
[33]Fedorov A.Transition and stability of high-speed boundary layers[J].Annu.Rev.Fluid Mech, 2011, 43:79-95.
[34]Zhong X, Wang X.Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers[J].Annu.Rev.Fluid Mech, 2012, 44(1): 527-561.
[35]Su C H, Zhou H.Transition prediction of a hypersonic boundary layer over a cone at small angle of attack-with the improvement of eNmethod[J].Science in China Series G, Physics Mechanics & Astronomy, 2009, 52(1): 115-123.
[36]King R A.Three-dimensional boundary-layer transition on a cone at Mach 3.5[J].Experiments in Fluids, 1992, 13: 305-314.
[37]Li X L, Fu D X, Ma Y W.Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J].Physics of Fluids, 2010, 22: 02515.
[38]Kachanov Y S, Michalke A.Three-dimensinoal instability of flat-plate bounday layers: Theory and experiment[J].Eur.J.Mech.B-Fluid., 1994, 13(4): 401-422.
[39]Gaster M.On the growth of waves in boundary layers: a non-parallel correction[J].Journal of Fluid Mechanics, 2000, 424: 367-377.
[40]Bertolotti F P, Herbert T, Spalart P R.Linear and nonlinear stability of the blasius boundary layer[J].Journal of Fluid Mechanics, 1999, 242: 441-474.
[41]Tang D B, Ma Q R, Chen G W.Study of compressible nonparallel flow stability for boundary layers[J].Acta Aeronautica et Astronautica Sinica, 2002, 23(2): 166-139.(in Chinese)唐登斌, 马前容, 成国玮.可压缩非平行流边界层稳定性研究[J].航空学报, 2002, 23(2): 166-139.
[42]Herbert T.Parabolized stability equations[J].Annu.Rev.Fluid Mech, 1997, 29(1): 245-283.
[43]Saric W S, Reed H L, White E B.Stability and transition of three-dimensional boundary layers[J].Annu.Rev.Fluid Mech, 2003, 35(1): 413-440.
[44]Huang Z F, Wu X.A non-perturbative approach to spatial instability of weakly non-parallel shear flows[J].Phys.Fluids, 2015, 27: 054102.
[45]Yu G T, Gao J, Luo J S.Stability analysis method considering non-parallelism: expansion of parabolized stability equation method and its application[J].Appl.Math.Mech.-Engl., 2016, 37(1): 27-36.
[46]Cebeci T, Stewartson K.On stability and transition in three-dimensional flows[J].AIAA Journal, 1980, 18(4): 398-405.
[47]Malik M R, Balakumar P.Instability and transition in three-dimensional supersonic boundary layers.AIAA 1992-5049[R].Reston: AIAA, 1992.
[48]Zhang S L, Huang Z F, Luo J S.A linear stability method considering the equivalent spread wave number in the three-dimensional boundary layer[C]//China Mechanics Conference, CASTAM2015-A21-E2791, 2015.(in Chinese)张绍龙, 黄章峰, 罗纪生.三维边界层中考虑等效展向波数的线性稳定性方法[C]//中国力学大会, CASTAM2015-A21-E2791, 2015[49]Scott B, Kamran D, Kathryn W.Boundary layer transition on X-43A.AIAA 2008-3736[R].Reston: AIAA, 2008.
[50]Luo J S, Wang X J, Zhou H.Inherent mechanism of breakdown in laminar-turbulent transition of plane channel flows[J].Science in China Series G, Physics Mechanics & Astronomy, 2005, 48(2): 228-236.
[51]Huang Z F, Cao W, Zhou H.The mechanism of breakdown in laminar-turbulent transition of a supersonic boundary layer on a flat plate-temporal mode[J].Science in China Series G, Physics Mechanics & Astronomy, 2005, 48(5): 614-625.
[52]Cao W, Huang Z F, Zhou H.Study of mechanism of breakdown in laminar-turbulent transition of supersonic boundary layer on flat plate[J].Applied Mathematics and Mechanics-English Edition, 2006, 27(4): 425-434.
[53]Dong M, Luo J S.Mechanism of transition in a hypersonic sharp cone boundary layer with zero angle of attack[J].Applied Mathematics and Mechanics-English Edition, 2007, 28(8): 1019-1028.
[54]Su C H, Zhou H.Transition prediction for supersonic and hypersonic boundary layers on a cone with angle of attack[J].Science in China Series G, Physics Mechanics & Astronomy, 2009, 52(8): 1223-1232.
——基于与QuestionPoint的对比

