超声速/高超声速边界层转捩后期流场的模态分析

余 明, 黄伟希, 许春晓

(清华大学 航天航空学院, 北京 100084)

0 引 言

高速可压缩边界层流动的转捩存在多种不稳定机制，而且非线性作用关系复杂[1-2]，人们开展了一系列的工作对转捩机理及预测方法进行研究[3-4]。对流场进行模态分解可使人们抓住流场中重要的物理机制和流动结构，是转捩机理的研究的重要手段[5]。目前常用的模态分解方法主要有两种：本征正交分解(Proper Orthogonal Decomposition，POD)和动力模态分解(Dynamic Mode Decomposition，DMD)。POD是基于能量的模态分解方法，而DMD是基于频率和增长率的模态分解方法[6]。

DMD方法首先由Rowley和Schmid等提出[6-7]，并应用于圆柱尾迹、方腔流动、射流等流动问题，相继又有很多学者提出了对该方法的修正和应用，但是在可压缩边界层转捩方面的应用较少。He等[8]用实验方法分析了由圆柱尾迹诱导的不可压缩平板边界层转捩，然后用DMD进行数据分析，发现第一增长阶段的频率与圆柱尾涡脱落频率一致，第二增长阶段存在多个频率的扰动。Sayadi等[9]对Ma=0.3的可压缩平板边界层H-型和K-型转捩的直接数值模拟数据进行DMD和三重分解分析，获得了相干结构对雷诺切应力的贡献，发现与发卡涡腿对应的低频模态对雷诺切应力贡献最大，并用低频模态准确预测了整个转捩过程中沿壁面法向雷诺应力的变化；Subbareddy等[10]对Ma=6.0孤立粗糙元引起的平板边界层转捩进行了动力模态分解，并提取出了能量占优模态的高频流场结构。

本文应用DMD方法对Ma=2.25和Ma=6平板边界层转捩后期(非线性发展阶段)流场进行分析。通过各阶模态我们可以清楚地看到流场结构与壁面阻力和热流之间的关系，以及超声速和高超声速边界层转捩中流动结构的差异。Ma=2.25的边界层转捩中的流场结构与亚声速和不可压流动相似，而Ma=6.0的边界层转捩流场中存在多种不稳定的模态，对转捩流场结构和转捩机制都有很大影响。

1 物理模型和模态分析方法

1.1 物理模型和计算参数

本文中选取的物理模型为超声速和高超声速平板边界层，采用直接数值模拟(Direct Numerical Simulation, DNS)方法求解完全气体可压缩守恒型N-S方程，以获取后文分析使用的流场数据样本。DNS的求解采用中科院力学所李新亮研究员开发的Opencfd软件[11-12]，并参考文献[13]和文献[14]选取相应的数值方法和计算参数。计算域如图1所示，初始流场为层流，入口为二维层流剖面，壁面为无滑移等温条件，壁温取为流场的恢复温度，上边界和出口为无反射边界条件，出口附加网格间距增大以衰减湍流脉动，避免出口对流场的影响；展向边界为周期性条件。采用有限差分方法求解方程，无粘通量采用七阶WENO格式，粘性通量采用六阶中心差分格式，时间推进采用三步TVD RK格式，具体算法说明参见文献[11]。

求解无量纲控制方程，各物理量用来流密度、速度和温度进行无量纲化，特征长度取为1 mm。本文主要选取了两组参数进行计算和分析：一组是超声速边界层，参考文献[13]中的实验选取计算参数，Ma=2.25，Re=25000/mm，来流温度T∞=169.4K，壁面相对温度Tw/T∞=1.9，流向(x)、法向(y)和展向(z)计算域范围分别为x=101.6～406.4,y=0～5.0,z=0～9.4，网格数分别为2193、72和256。在入口下游给定壁面吹吸的扰动，形式为[15]：

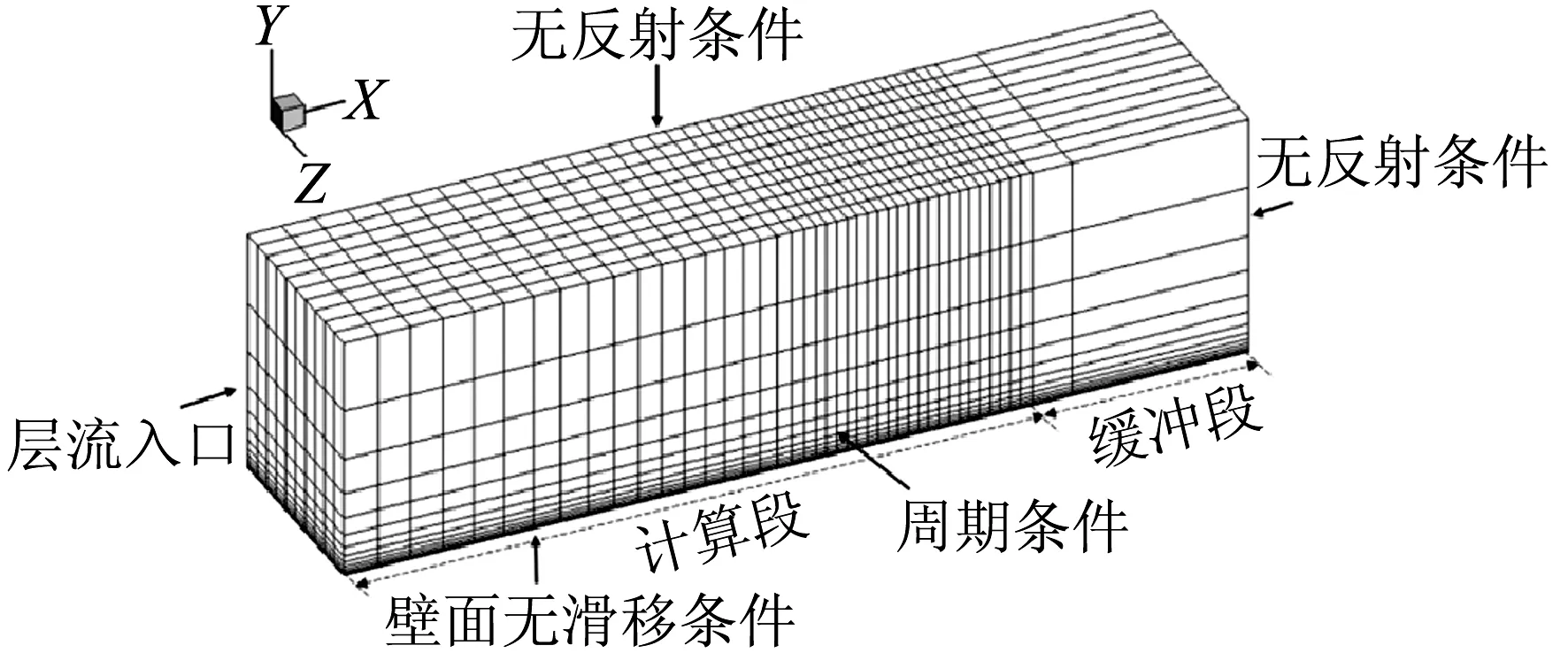
图1 计算域和网格示意图Fig.1 Sketch of computational domain and meshes

vb=Aaf(x)g(z)h(t)

(1)

其中Aa为扰动幅值，其他各项为：

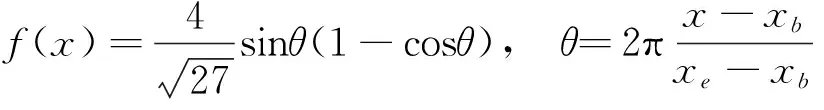
(2)

(4)

其中kz为扰动的展向波数，zmax为展向计算域长度，βm为扰动的频率，xb～xe为扰动沿流向的范围，φl和φm为扰动的相位。在此算例中，取各参数如下：

xb=114.3,xe=127.0,lmax=3,mmax=3；

β1=0.155,kz1=0,φ1=φ1=0,

Aa=1,A1=0.004；

β2=β3=0.309,kz2=kz3=1,φ2=φ3=0,

φ2=0,φ3=π/2,A2=A3=0.004。

吹吸扰动的强度较大，转捩过程为从非线性阶段开始的bypass转捩。如图2所示为壁面摩擦阻力系数(Cf)沿流向的分布，转捩起始的位置为x=165，转捩后湍流部分Cf的分布与文献[15]中给出拟合曲线相吻合。图3中展示了从扰动起始到转捩结束的流向范围(x=114～178)的涡结构(由速度梯度张量的第二不变量Q的等值面表示)，可以看到在转捩开始位置的上游为规整的流向涡，逐渐抬升并发展出碎小的涡结构。各个主涡诱导的小涡在展向的范围逐渐增加，在下游形成完全紊乱的流动。

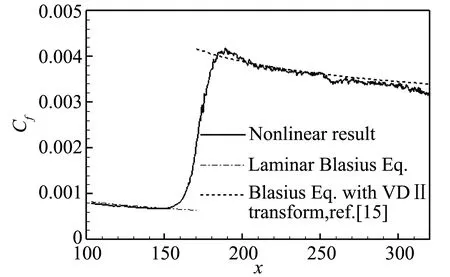
图2 壁面阻力系数曲线(Ma=2.25)Fig.2 Profile of skin friction coefficient (Ma=2.25)

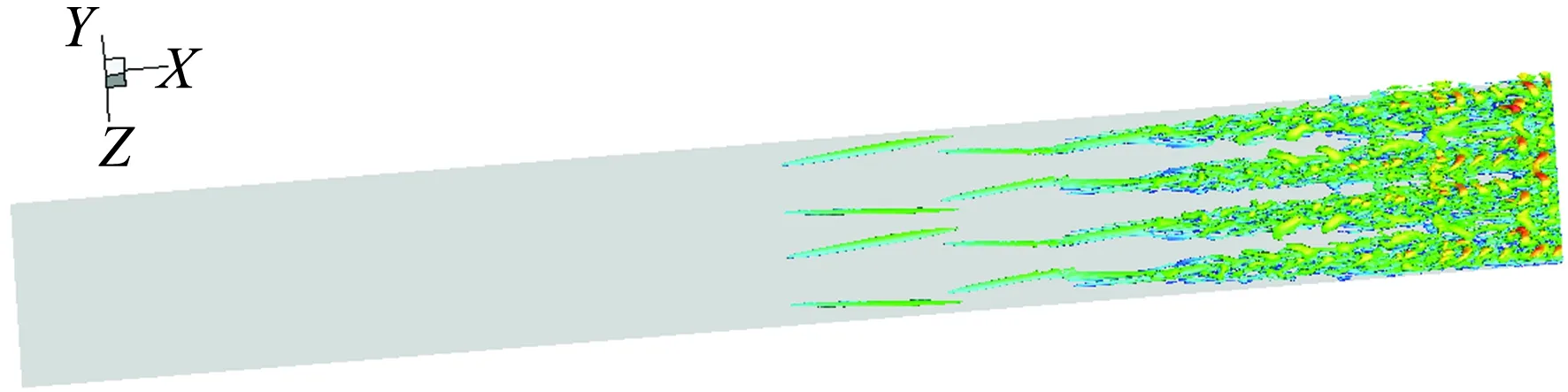
图3 转捩流场涡结构(Q=0.02)Fig.3 Vortex structure on transitional flow (Q=0.02)

另一组是高超声速边界层，Ma=6，Re=10000/mm，来流温度T∞=79 K，壁温Tw/T∞=3.72。流向(x)、法向(y)和展向(z)计算域范围分别为x=240～1600,y=0～36,z=0～30，网格数分别为4482、140和256。在入口下游x=260～280壁面加随机吹吸扰动，即式(1)中g(z)和h(t)替换为随机函数，随机数的幅值取为0.04。

如图4所示为壁面阻力系数Cf沿流向的变化。在扰动下游x=260～800的范围内Cf曲线与层流解一致，没有明显的变化，转捩开始的位置为x=850。图5中展示了z=15平面上的密度和速度分布，可见在x<600的区域流场与层流没有明显的差别，x=600～800范围内可以观察到小幅的扰动波。速度的扰动波只在边界层内比较明显，而密度的扰动波明显可以分为两个区域：一是边界层内贴近壁面的部分，与速度的扰动波相似；二是边界层外缘的部分，对应着边界层外向外转播的Mach波[16]。Duan等的研究表明，在充分发展的湍流边界层中，Ma越高边界层外缘的湍流间歇性和边界层内外的膨胀和压缩波越强[17]，这与密度的脉动是密不可分的，因此后文中我们重点讨论各阶模态中流向速度和密度的扰动形式。

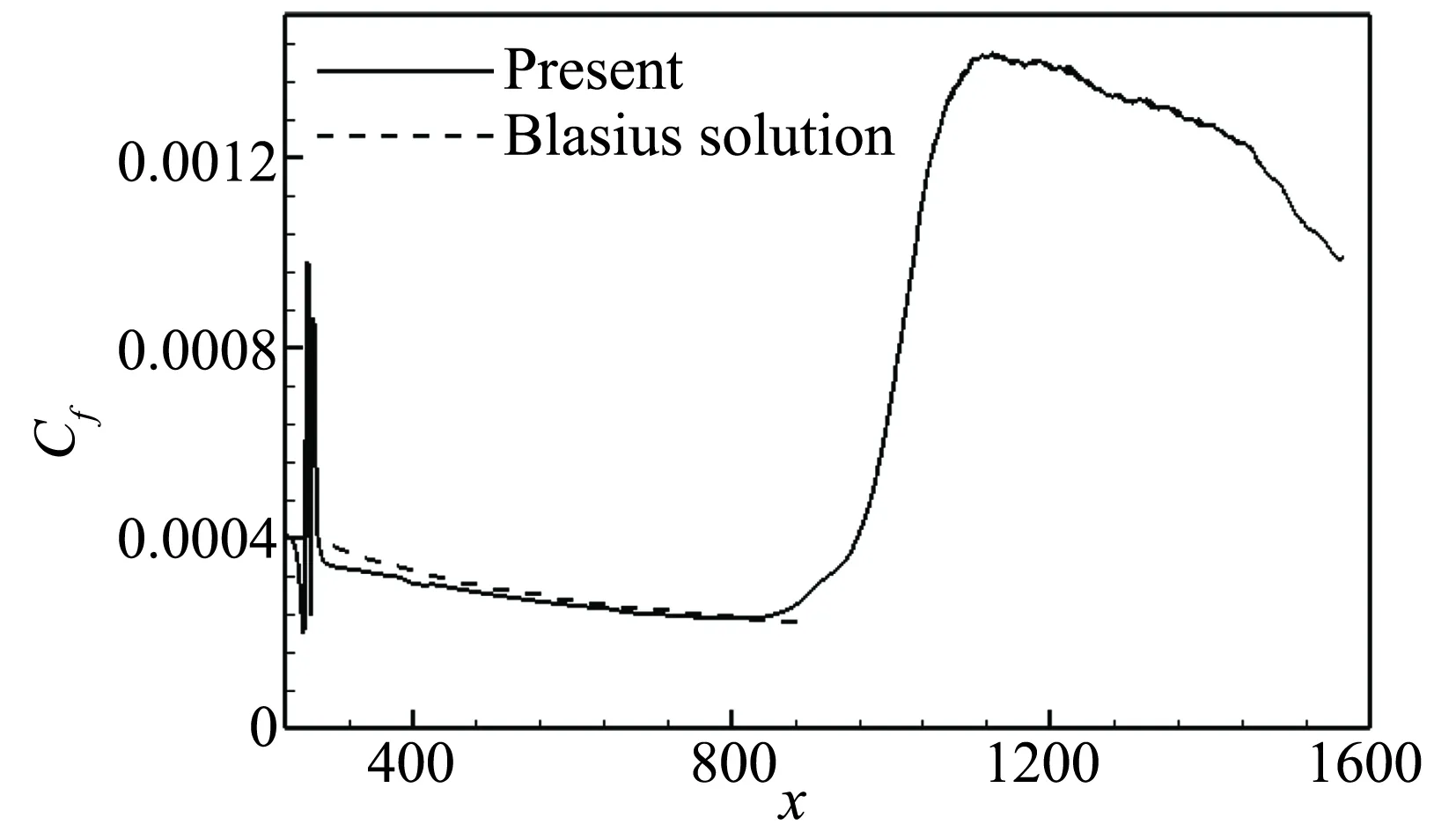
图4 壁面阻力系数曲线(Ma=6)Fig.4 Profile of skin friction (Ma=6)

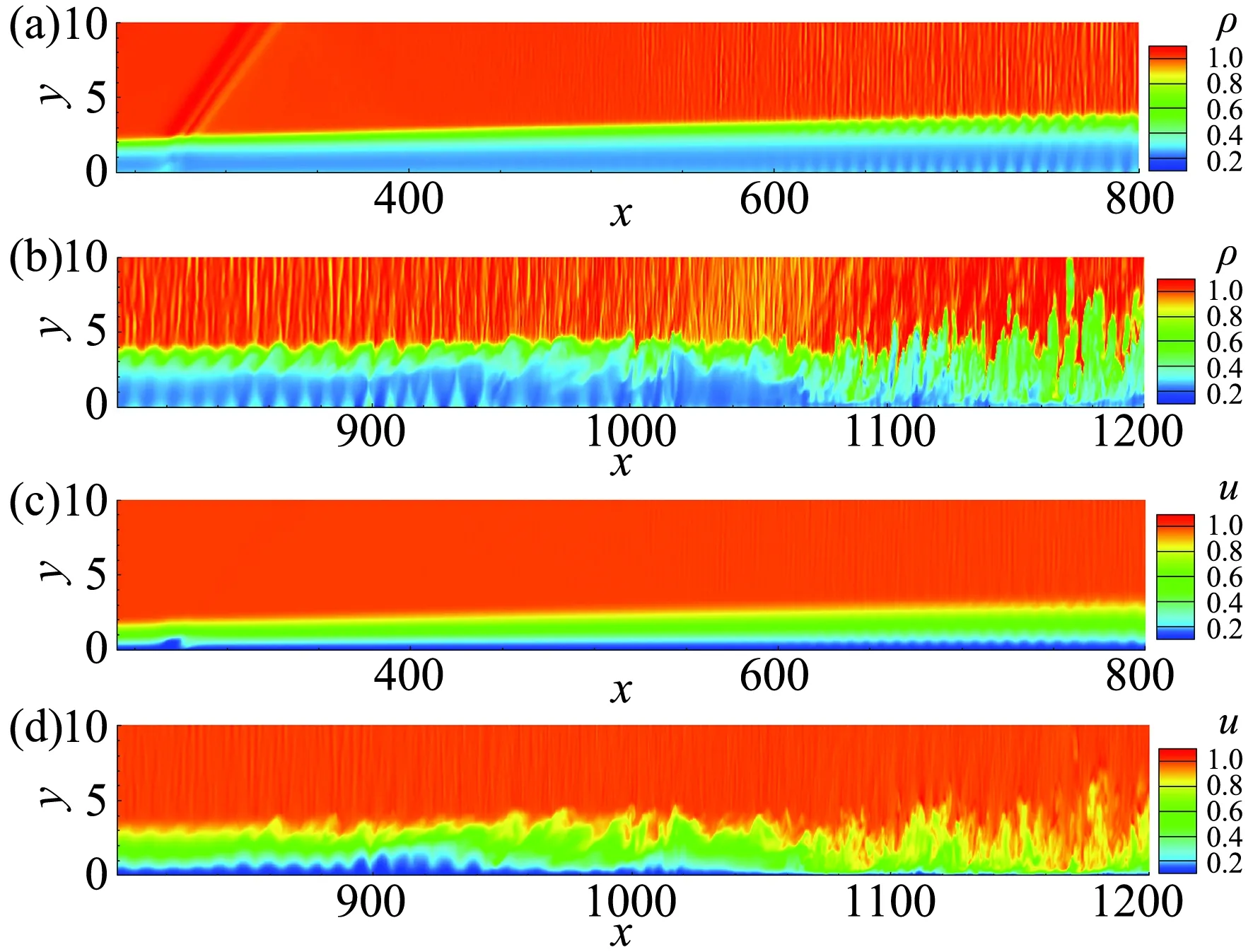
图5 密度和流向速度的瞬时场(z=15.0)Fig.5 Instant flow field of density andstreamwise velocity (z=15.0)

1.2 DMD原理和算法简介

动力模态分解是通过对流场的数据样本进行分析，提取流场中具有不同频率和增长率的流动结构的方法。若已知流场中的(m+1)个不同时刻的数据样本x0,x1,…,xm，为了提取流场中随时间演化的主要结构，可将数据样本写成矩阵的形式：

X=[x0,x1,…,xm-1]，X′=[x1,x2,…,xm]

(5)

若样本的时间间隔Δt很小，则可以认为从X到X′可以经过一个线性映射得到，即

X′=CX

(6)

求解矩阵C的特征值问题，便可以得到不同特征值μi(i=1,2,…,m)及其对应的特征模态。特征值μi表示模态随时间的演化，|μi|>1表示模态是不稳定的，|μi|=1是中性稳定的，|μi|<1是稳定的。取:

ωi=lg(μi)/Δt

(7)

其实部表示模态的增长率，虚部表示模态的频率。

在实际求解过程中，矩阵C是未知的，由式(5)中矩阵求伪逆得到的C通常是病态的，这给求解特征值问题带来很大麻烦。因此在计算时，首先对样本矩阵进行预处理。目前有两种预处理方法，一是对样本矩阵进行QR分解[6]，二是对样本矩阵进行奇异值分解[18]。本文采用第二种方法，具体算法如下：

1) 将数据矩阵X作奇异值分解：X=UΣVH，其中U和V的列向量相互正交，上标H表示矩阵的共轭转置，Σ为以奇异值为对角线元素的对角阵；

2) 计算C矩阵在U上的投影为C′=UHX′VΣ-1；

3) 求解C′的特征值和特征向量C′W=WΛ，Λ为特征值矩阵，W为DMD模态在U上的投影，进一步计算DMD特征模态Φ=X′VΣ-1W。

4) 按需要将特征值和特征模态进行排序，本文采用文献[19]中的Sparsity-Promoting DMD(SPDMD)的方法对模态进行选择，并按模态的能量大小进行排序。SPDMD是在一般的DMD方法基础上，引入了“促进稀疏”的方法，通过罚函数来选择“不重要的”模态：衰减很快的模态和能量较小的中性稳定模态会被筛选并去除，保留下来的模态一般是能量较高的中性稳定模态和增长的模态。

2 Ma=2.25边界层转捩的模态分析

本小节应用DMD对Ma=2.25边界层转捩的流场结构进行分析。首先应用上文中的DNS数据，取201个等时间间隔的数据样本进行分析。在DMD分析中我们仅取从扰动结束到转捩开始的流向范围进行分析，即流向x=127～165的范围和法向、展向的全计算域。考虑到吹吸扰动的频率和高频波的时间分辨率，取时间间隔Δt=1.27，总时间跨度ΔT=254。模态分析采用的数据为每个网格点上三个方向的速度(u,v,w)、密度ρ和温度T。

如图6(a)所示为DMD特征值，由SPDMD选出的主要模态由○圈出，散点的颜色表示模态初始能量的大小。计算结果表明，主要模态的特征值都分布在单位圆上，表明这些模态都是中性稳定的。进一步在图6(b)中展示了DMD的频谱，横坐标为模态的频率，纵坐标为模态的初始幅值A(由SPDMD算法给出)，黑色实心圆为SPDMD选出的模态，这些模态在频率上分布范围较大，但是能量较高的模态都集中在低频范围，高频模态的能量较小。我们进一步考察低阶模态扰动能量之和，定义扰动动能Ek、内能Ee和总能Et如下：

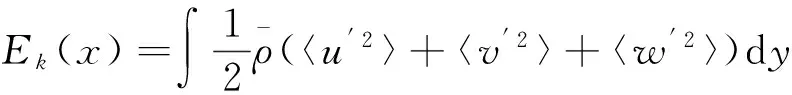
(8)

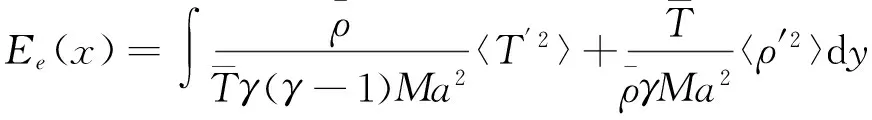
(9)

Et(x)=Ek(x)+Ee(x)

(10)

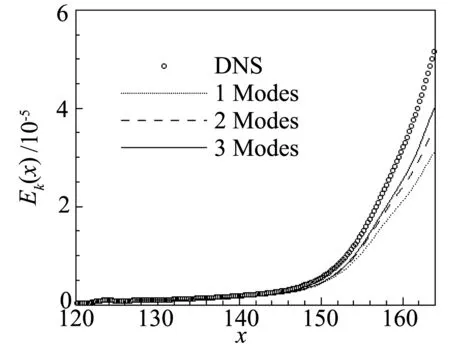
图7 模态重构扰动能量(Ma=2.25)Fig.7 Mode reconstruction of disturbanceenergy (Ma=2.25)

下面我们选取了两个典型模态进行分析，分别为低频模态和频率相对较高的模态，在图6(b)中用○圈出。为了方便表述，我们称这两个低频和高频的模态分别为Mode1和Mode2。

如图8(a)所示为Mode1的涡结构，可见这些涡结构都是沿流向拉长的，图8(b)和8(c)中分别为该模态引起的壁面摩擦阻力系数和热流的分布，可以看到这些涡结构与摩擦阻力系数和热流升高的区域存在明显的相关性。涡结构引起的流向速度剖面变化是壁面阻力系数变化的主要原因，因此涡结构强的区域壁面阻力系数变化也大，壁面热流与壁面阻力系数类似。由于此时流体质点本身的温度脉动较小，对热流的作用可以忽略不计，涡结构对流体质点物理量的输运是引起热流变化的主要原因，温度脉动和速度脉动具有很强的相关性，因此壁面阻力系数和热流都与涡结构有明显的相关性。我们进一步对其他低频模态进行了考察(本文中未展示)，结果表明低频高能量的模态与Mode1类似，随着频率的增加，涡结构的流向尺度逐渐变小。这些模态中结构对壁面阻力系数和热流在x=130到转捩x=165都有很重要的影响。而对于如Mode2的高频低能量的模态(如图9所示)，涡结构尺度小且密集，主要集中在x=155～165的范围内。这些涡结构是转捩过程中非线性效应的衍生物，它们在转捩前的法向位置高于低频高能量的模态，直到转捩开始时对壁面阻力和热流才有比较重要的影响。关于速度和温度脉动的相关性，可以在重构流场的能量中得以体现。如图10所示进一步展示了流向x=150位置处速度和温度脉动强度沿法向的变化，从二者脉动强度的分布上来看，速度和温度具有明显的相关性。

由以上分析可知，低频高能量的模态的流动结构是引起转捩的主要原因，而小尺度的结构则是这些模态衍生的结构。在非线性发展阶段，流场中的主要涡结构是流向拉长的，壁面阻力和热流的变化也与这些结构存在直接的关系。这一结论与Sayadi等对Ma=0.3边界层转捩后期的分析结论是一致的[10]，可见在超声速边界层中，转捩流场的结构和物理机制与亚声速和不可压的流动是类似的。

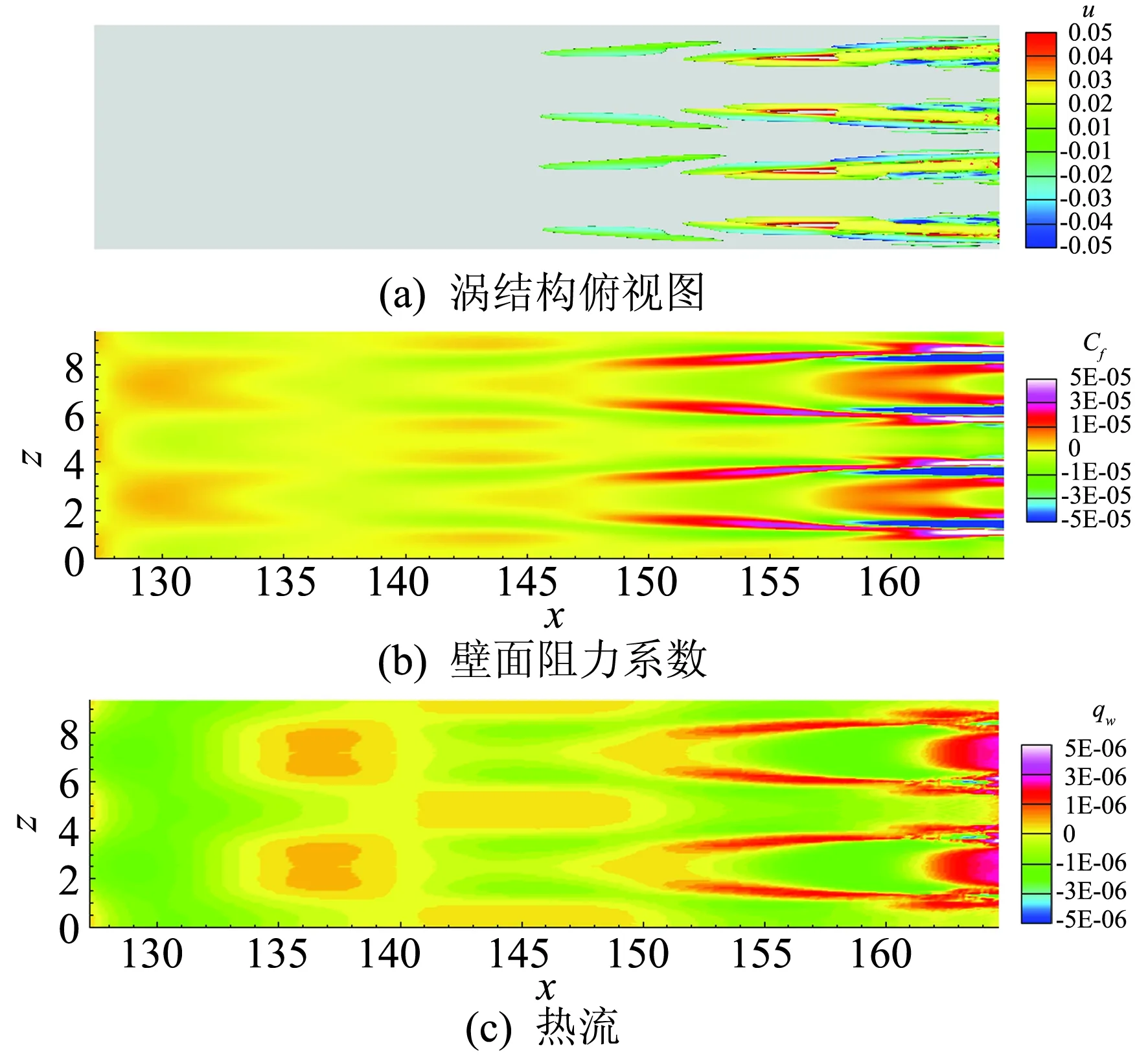
图8 Mode1的涡结构俯视图、壁面阻力系数和热流在壁面上的分布。(a)中涡结构采用Q=0.0001的等值面显示，采用流向速度u染色Fig.8 (a) Top view of vortex structure, (b)skin frictioncoefficient and (c)heat flux on the wall of Mode1, vortex in (a) is shown with isosurface of Q=0.0001, colored by streamwise velocity u

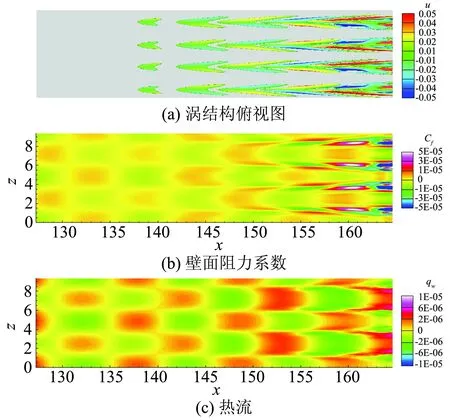
图9 Mode2的涡结构俯视图、壁面阻力系数和热流在壁面上的分布。(a)中涡结构采用Q=0.0001的等值面显示，采用流向速度u染色Fig.9 (a) Top view of vortex structure, (b)skin frictioncoefficient and (c)heat flux on the wall of Mode2, vortex in (a) is shown with isosurface of Q=0.0001, colored by streamwise velocity u

(a) 速度

(b) 温度

3 Ma=6 边界层转捩的模态分析

本小节对Ma=6边界层转捩的流场进行分析，选用的变量与Ma=2.25的DMD模态分析相同，分析的区域取为流向x=600～800的范围，法向和展向的全计算域。Ma=6边界层的吹吸扰动是随机的，因此数据样本的时间间隔选取不能直接由某个特征频率得到。高超声速边界层中多种不稳定模态的频率差别很大[20]，高低频模态的频率量级之比在103左右，受计算条件的限制，在DMD分析中很难完全地分辨出所有频率的模态。我们采用的做法是在保证主要高频模态分辨率的同时，尽量分辨低频模态。经过几次尝试，我们选取时间间隔Δt=1.5，总时间跨度ΔT=300，总时间样本数为201。

如图11(a)所示为DMD的特征值，由SPDMD选出的模态用○圈出，散点的颜色表示模态能量的大小。这些模态都是分布在单位圆上的，即时间上是中性稳定的。图11(b)中进一步展示了DMD的频谱。可见SPDMD选出的主要模态在频率上可以分为三个分支，一是低频的分支，集中在Im(w)=0附近，二是中等频率的分支，集中在Im(w)=0.6附近，三是高频的分支，集中在Im(w)=1.4附近。我们按能量大小对模态进行排序，并取2～4阶模态对流场的扰动能量进行重构，如图12所示。计算结果表明，在模态分析的区域内，扰动内能大于扰动动能，用3～4阶模态就可以较好地预测扰动能量随流向的变化。

下面我们对三个分支分别取能量最高的脉动模态(频率成对出现的模态)进行分析，在图11(b)中用○圈出，下文中分别称这三个模态为Mode1(低频)，Mode2(中等频率)和Mode3(高频)。

如图13所示为低频分支Mode1的流向速度(a)和密度(b)的分布。图中z=13.3展向截面，速度的扰动在边界层内外缘都较强，而密度的扰动只在边界层外缘较强。我们进一步在边界层内外分别取y=1.3和y=3.0两个法向截面，在这两个截面上速度和密度的扰动都是流向拉长的条带，流向速度在y=1.3的扰动强度大于y=3.0，而密度在y=3.0上的扰动强度大于y=1.3，这表现了低频模态扰动在法向位置分布的差异。从条带形式来看，速度和密度的扰动分布具有比较强的相关性，在转捩后期体现得更为明显。这些条带结构对壁面阻力和热流的影响如图14所示。可以看到在低频模态中，转捩初期也存在很明显的二维扰动波，在后期流向的条带结构占主导。二维扰动波在热流分布中流向延伸得更长，表明热流与速度的条带不完全对应，表明此时热力学量的脉动与速度脉动是同量级的，热流不仅有速度脉动输运的影响，还有流体质点温度脉动的影响。

(a) DMD特征值

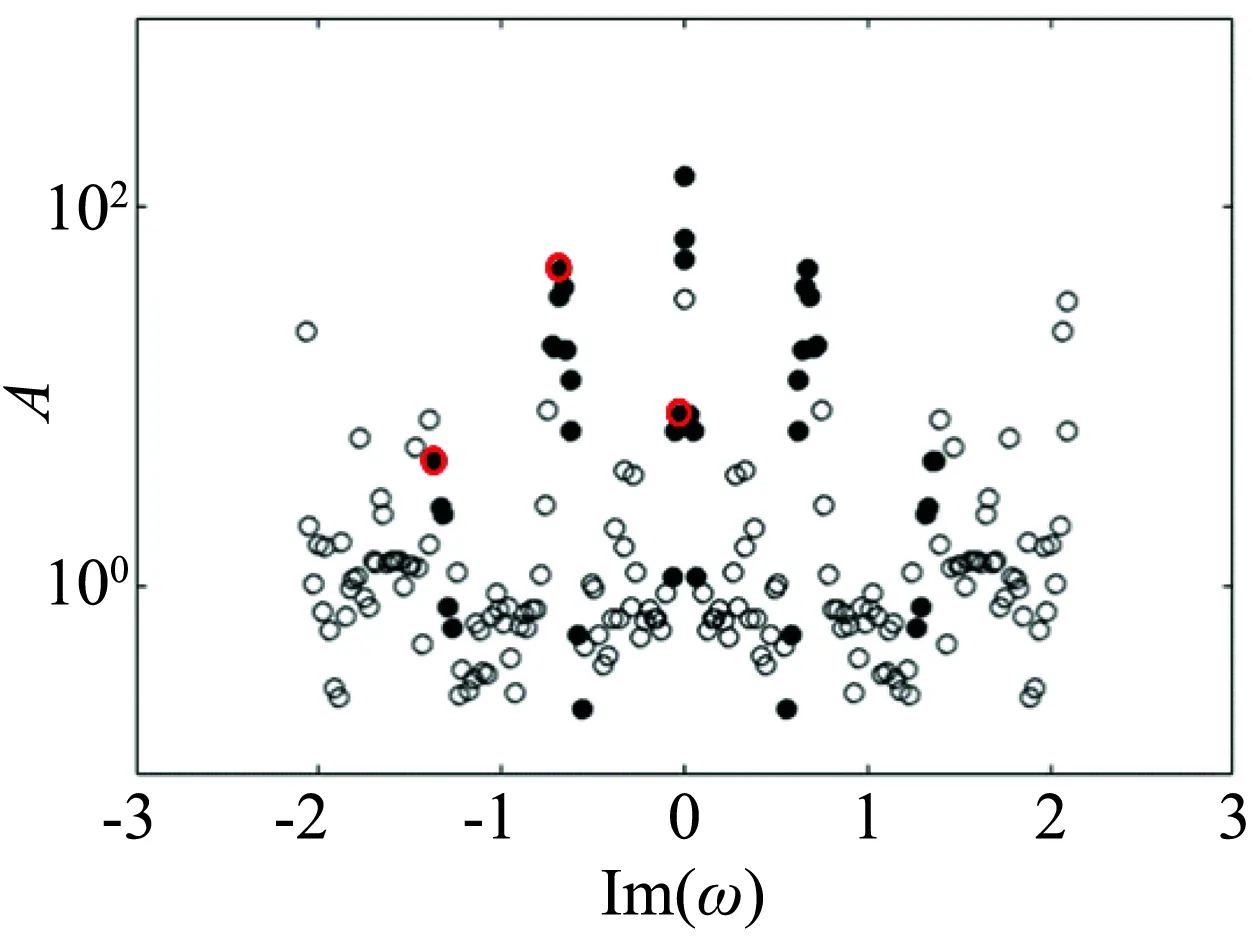
(b) DMD频谱

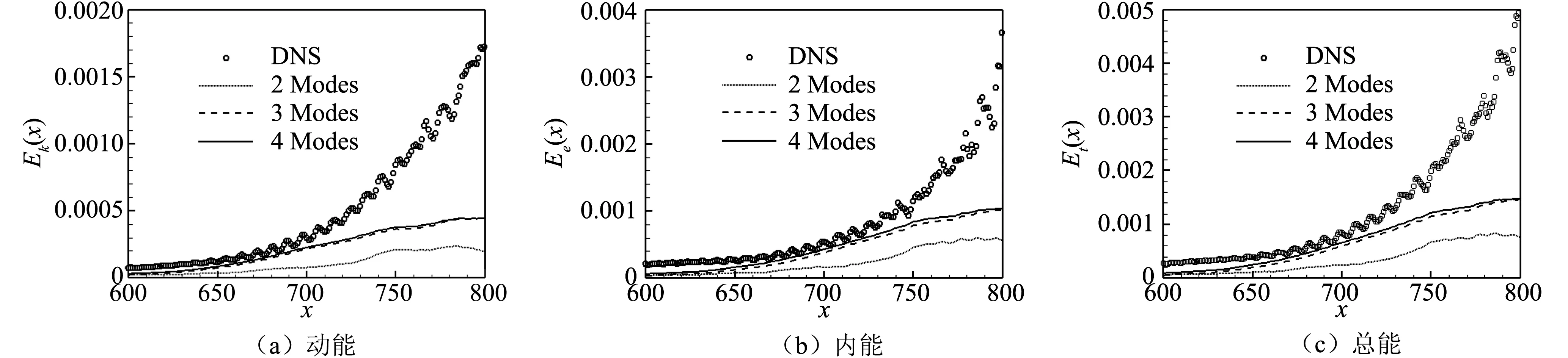
图12 模态重构扰动能量(Ma=6)Fig.12 Mode reconstruction of disturbance energy (Ma=6)

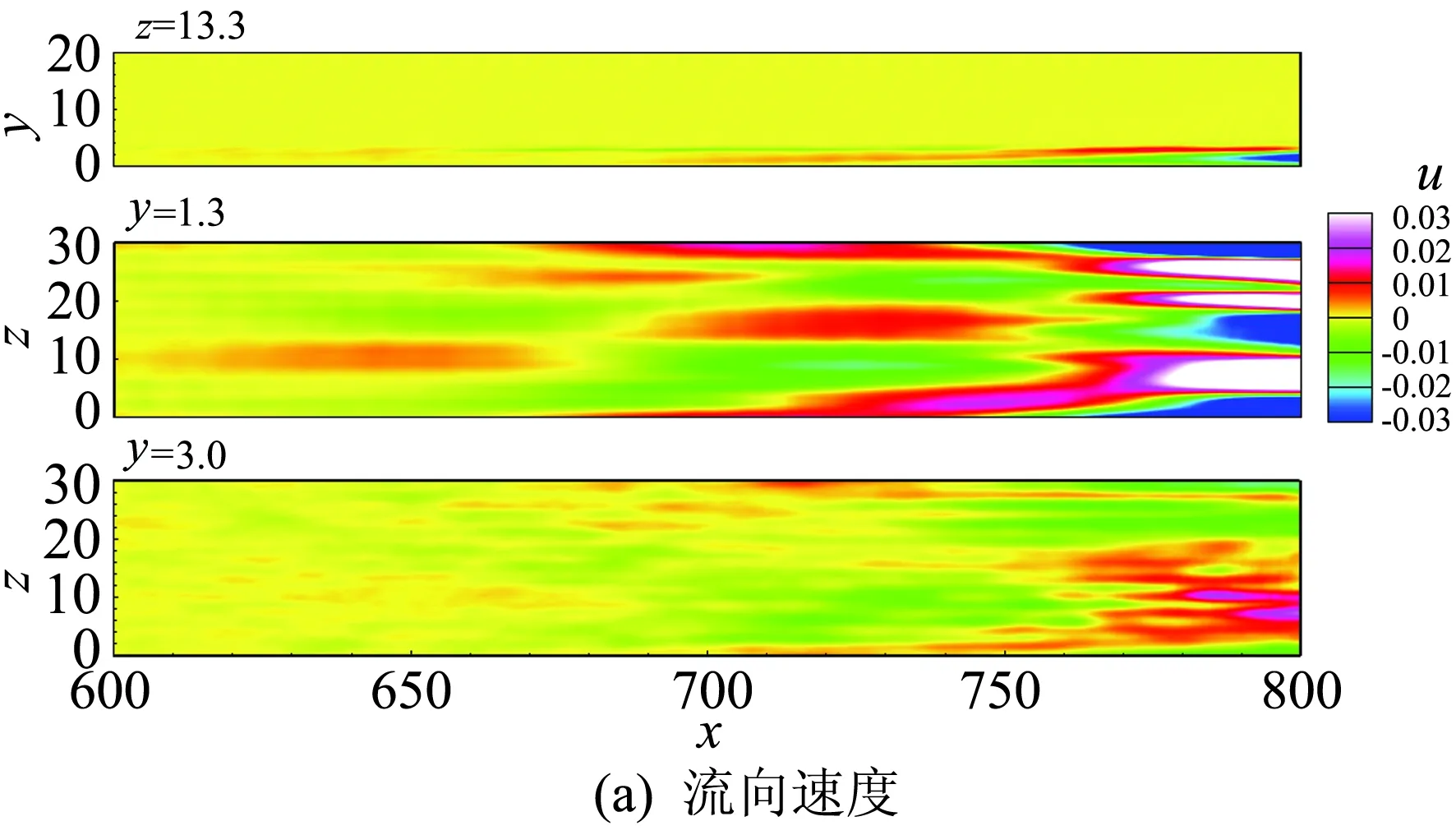
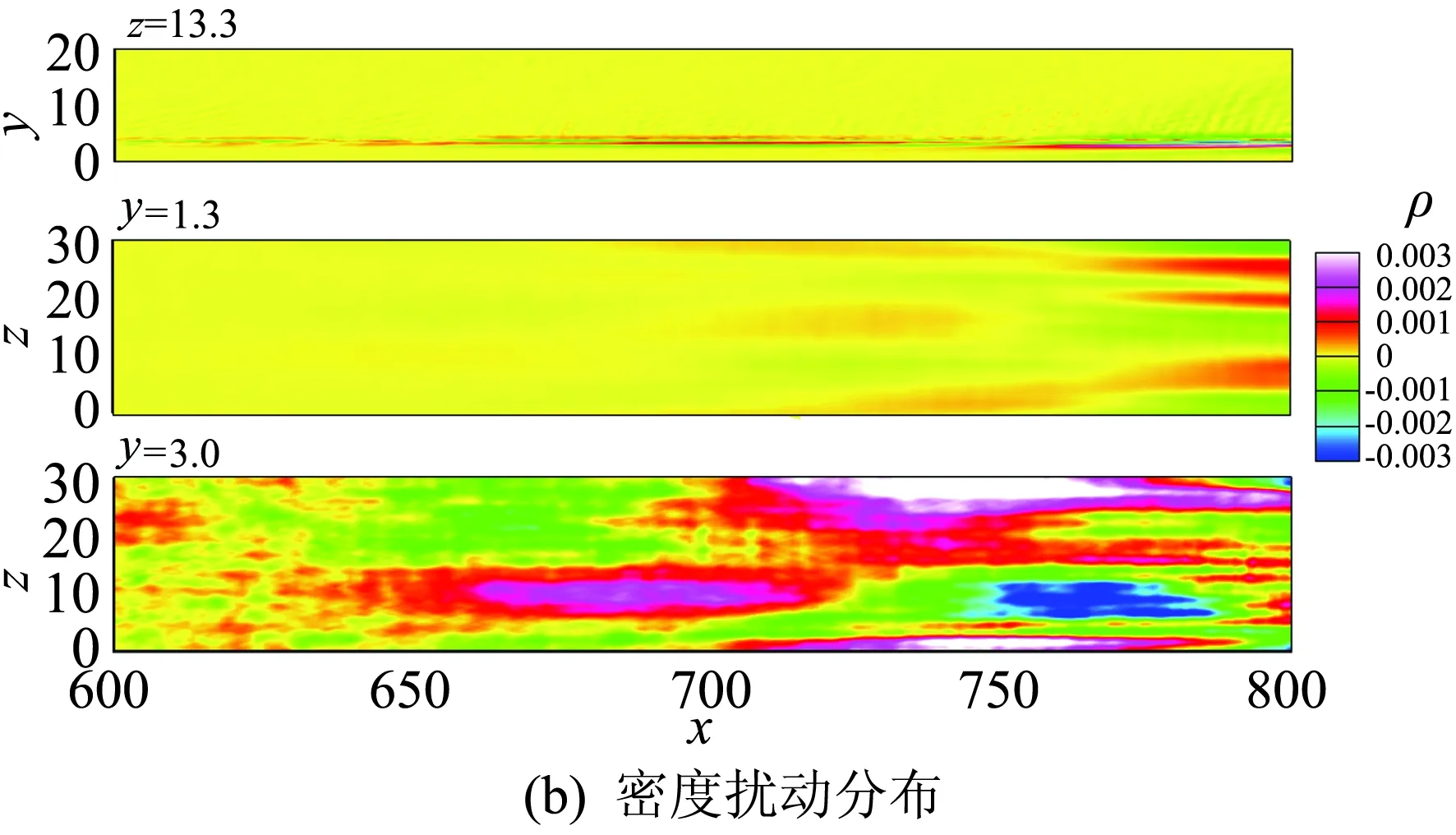
图13 Mode1的流向速度和密度扰动分布Fig.13 Contours of (a) streamwise velocity and (b) density and temperature of Mode1

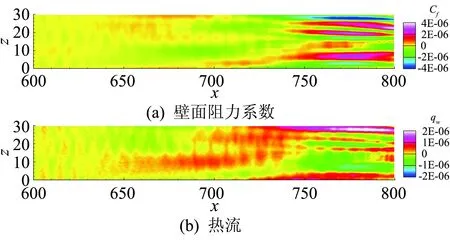
图14 Mode1的壁面阻力系数和热流Fig.14 (a) Skin friction coefficient and (b) Heat flux on the wall of Mode1

如图15所示为中等频率模态Mode2的速度和密度分布，所取的截面与图14一致。在此模态中，这些扰动波是二维的，流向波长远比低频模态小，速度的扰动在边界层内部较强，而密度的扰动在边界层内外都有较强的脉动，脉动延伸到边界层外缘并向外辐射，这些结构产生的壁面阻力和热流的分布(如图16所示)也是呈现为二维扰动波的形式。高频模态Mode3与Mode2类似(如图17所示)，高频模态与中等频率模态除了在尺度上的差异外，其他性质都是类似的。因此以下为了讨论方便，将中等频率模态和高频模态统称为高频模态。

图18中给出了壁面阻力和热流沿流向的相关系数，它们由图14和图16中高低频模态阻力和热流展向平均得到。从图中可以定量地看到，同不可压、亚声速和超声速边界层类似，在高超声速边界层中，低高频模态的壁面阻力和热流也具有明显的相关性。

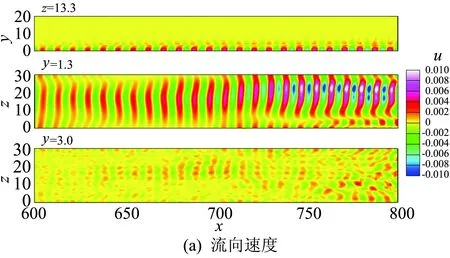
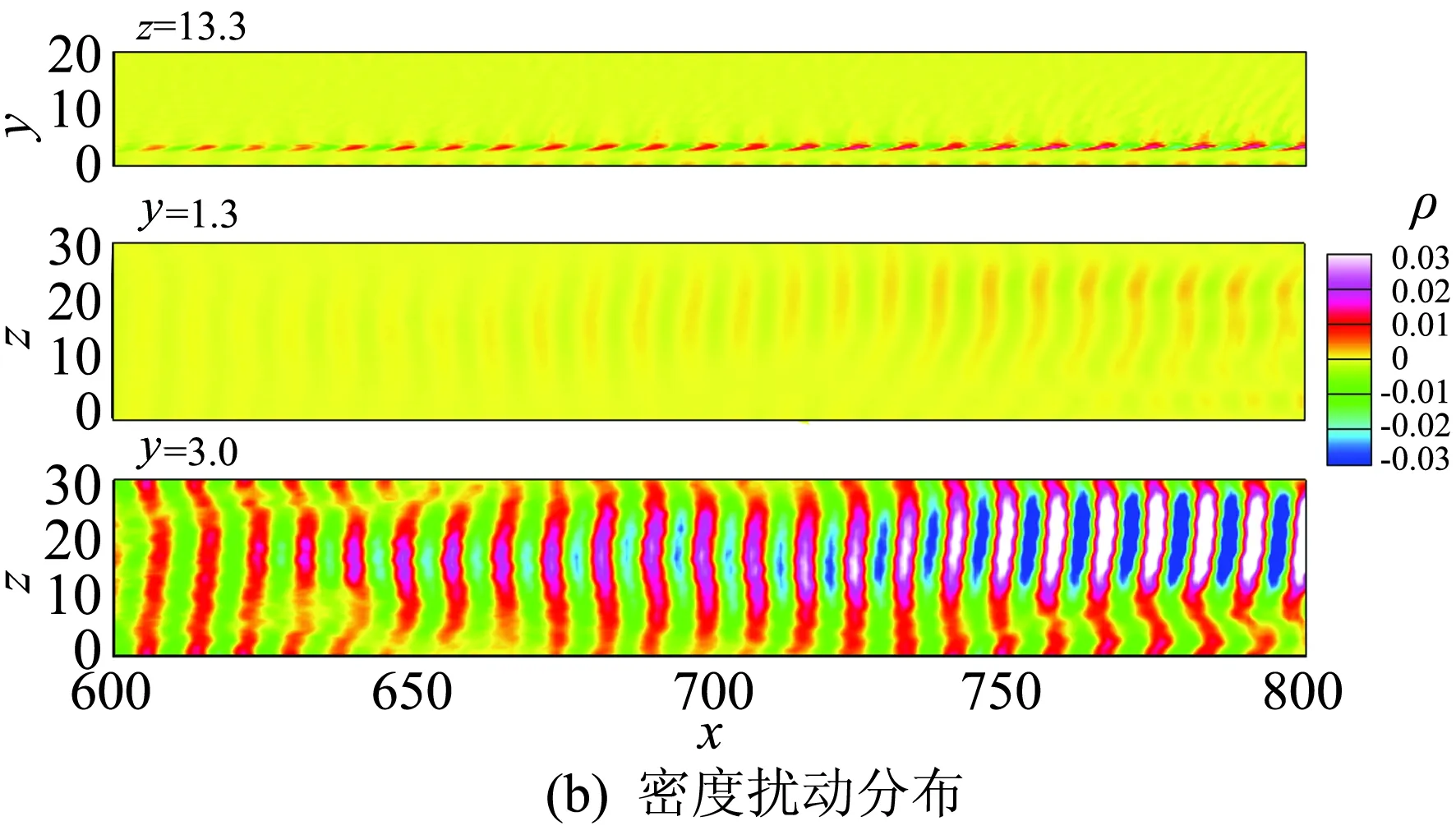
图15 Mode2的流向速度和密度扰动分布Fig.15 Contours of (a) streamwise velocity and (b) density and temperature of Mode2

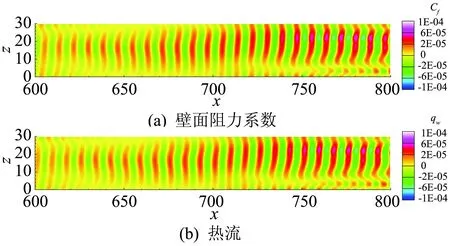
图16 Mode2的壁面阻力系数和热流Fig.16 (a) Skin friction coefficient and (b) Heat flux on the wall of Mode2

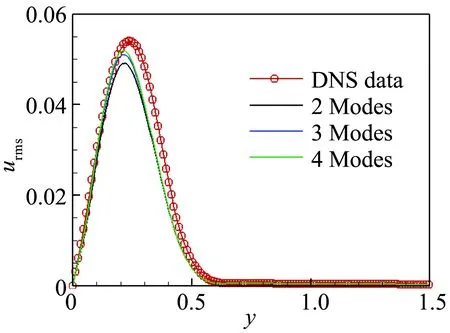
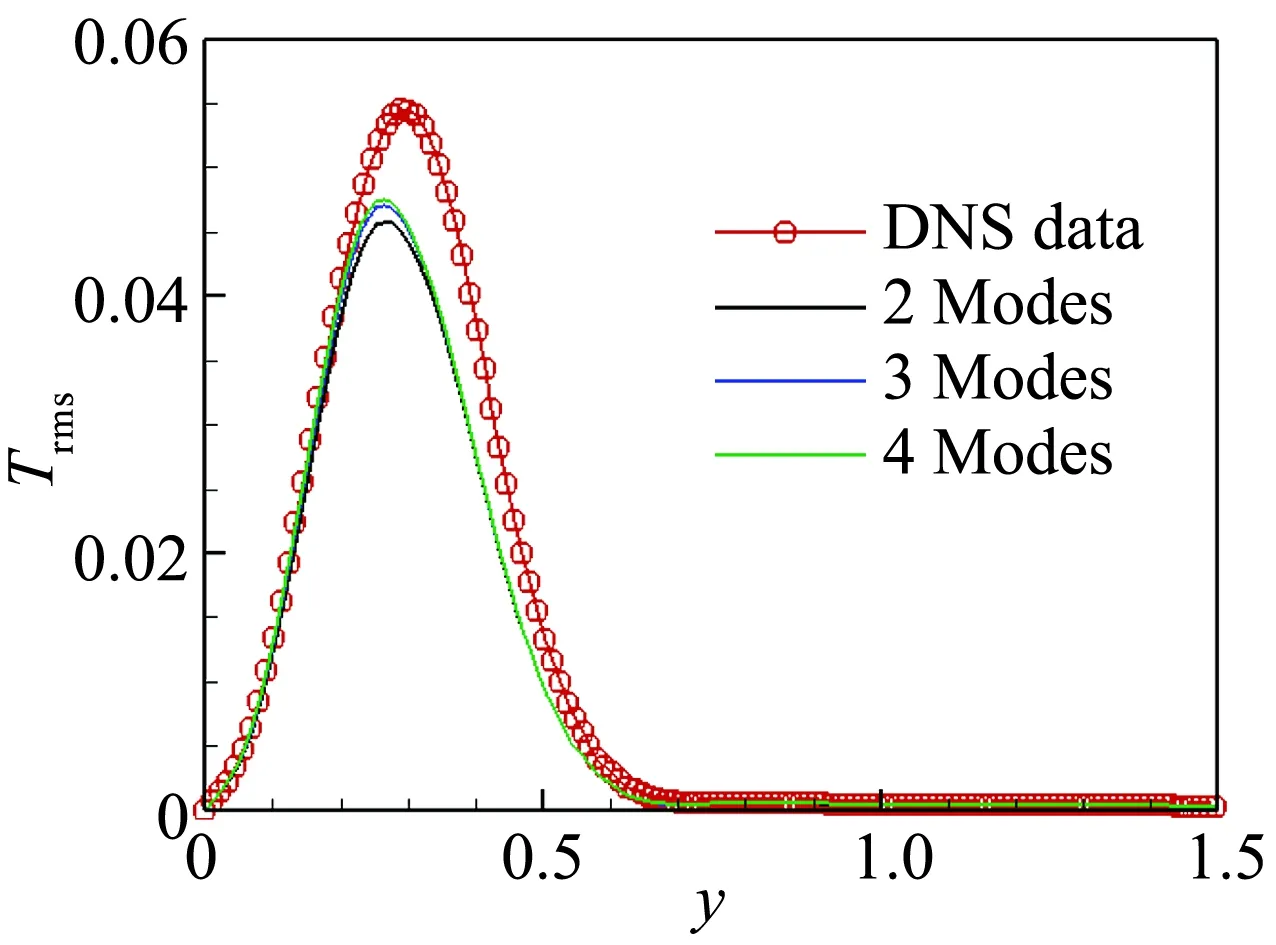
图19(a,b)中展示了流向x=700位置用2-4阶模态重构的密度和速度脉动均方根沿壁面法向的变化和与DNS结果的比较。密度和速度脉动沿法向的变化与上文中的定性分析结果相一致。图19(c)中进一步给出了温度脉动沿法向的变化，可以看到温度的脉动在壁面附近和边界层外缘分别存在一个峰值，前者体现了温度脉动对热流作用的影响，后者体现了边界层外缘剧烈的热量交换。值得注意的是，与上文中Ma=2.25的结果相差不同，速度和温度脉动沿法向的分布相关性很小，进一步证实了温度脉动不完全是由速度脉动输运引起的，还包括流体质点温度脉动的影响。

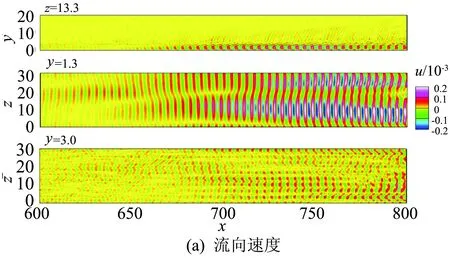
图17 Mode3的流向速度和密度扰动分布Fig.17 Contours of (a) streamwise velocity and (b) density and temperature of Mode3

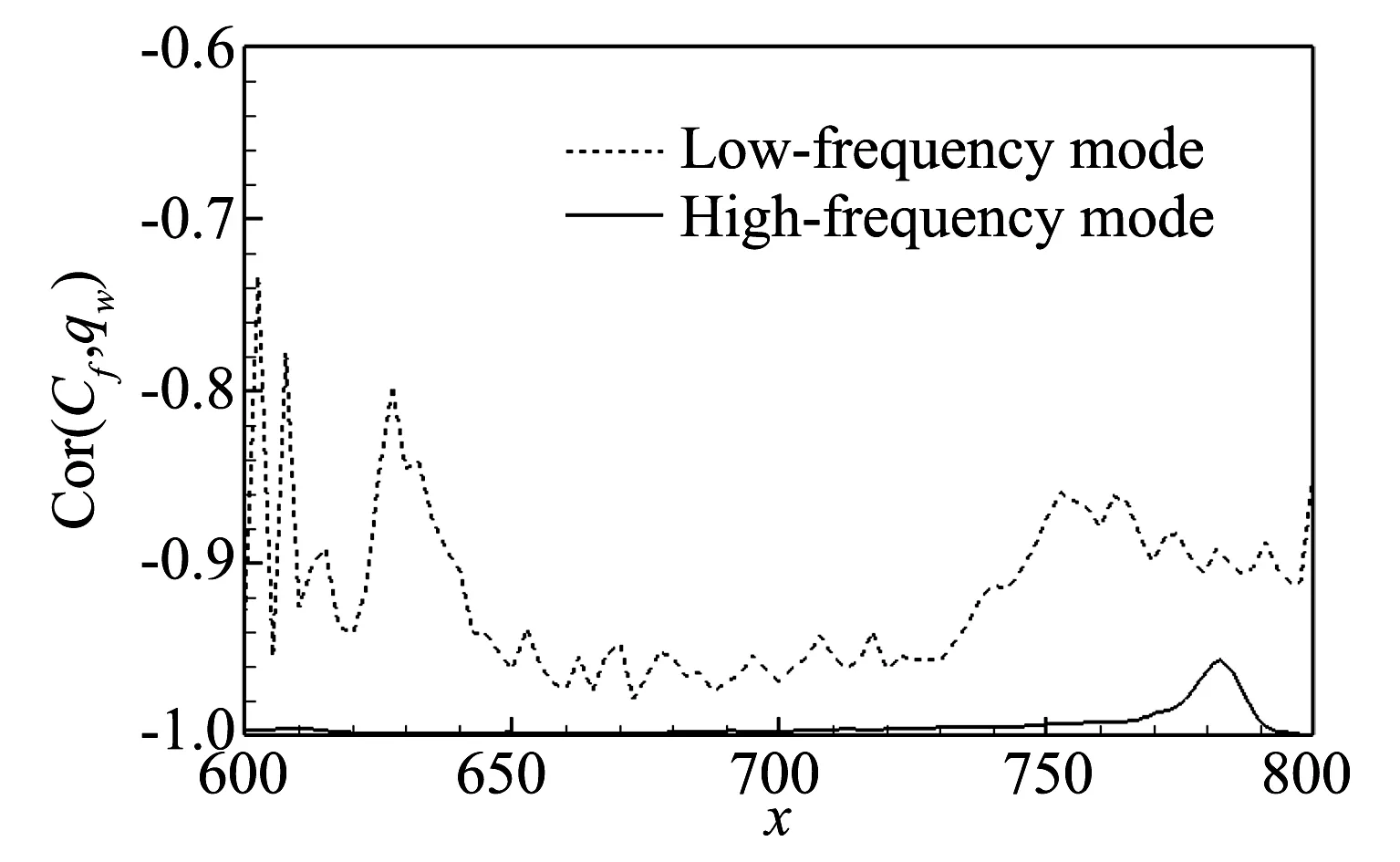
图18 壁面阻力和热流的相关系数Fig.18 Correlation coefficient betweenskin friction and heat flux

以上我们考察了Ma=6边界层转捩后期的高低频模态，可以看到转捩边界层中的扰动分布在两个法向位置，分别在壁面和边界层外缘。低频模态和高频模态在结构上存在明显的差异，低频模态的结构主要是流向的条带，而高频模态的结构则是二维扰动波。这一现象在Li 等[20]研究钝锥边界层转捩中就给出了类似的结论。Li等采用了滤波的方法研究了流场中沿流向和法向分布的几个点上的速度脉动信号，大尺度和小尺度表现为不同频率的正弦扰动，在本文中利用DMD方法得到的模态空间分布上可以看到，高低频模态的结构在空间上也分别对应于不同波长的正弦形式的扰动，与Li等的研究结果是一致的。值得注意的是，在计算的扰动区域是随机的吹吸扰动，可以认为是高频的脉动，即在边界层发展的初期是不存在低频成分的，随着扰动向下游的发展，低频结构逐渐出现，因此低频模态是不稳定高频模态诱导产生的。

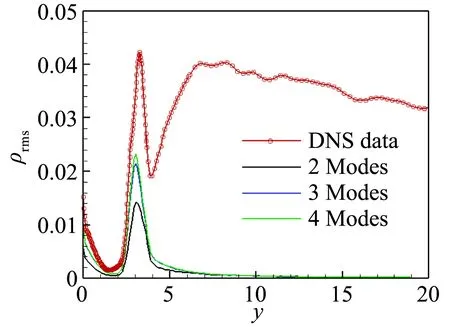
(a) 密度

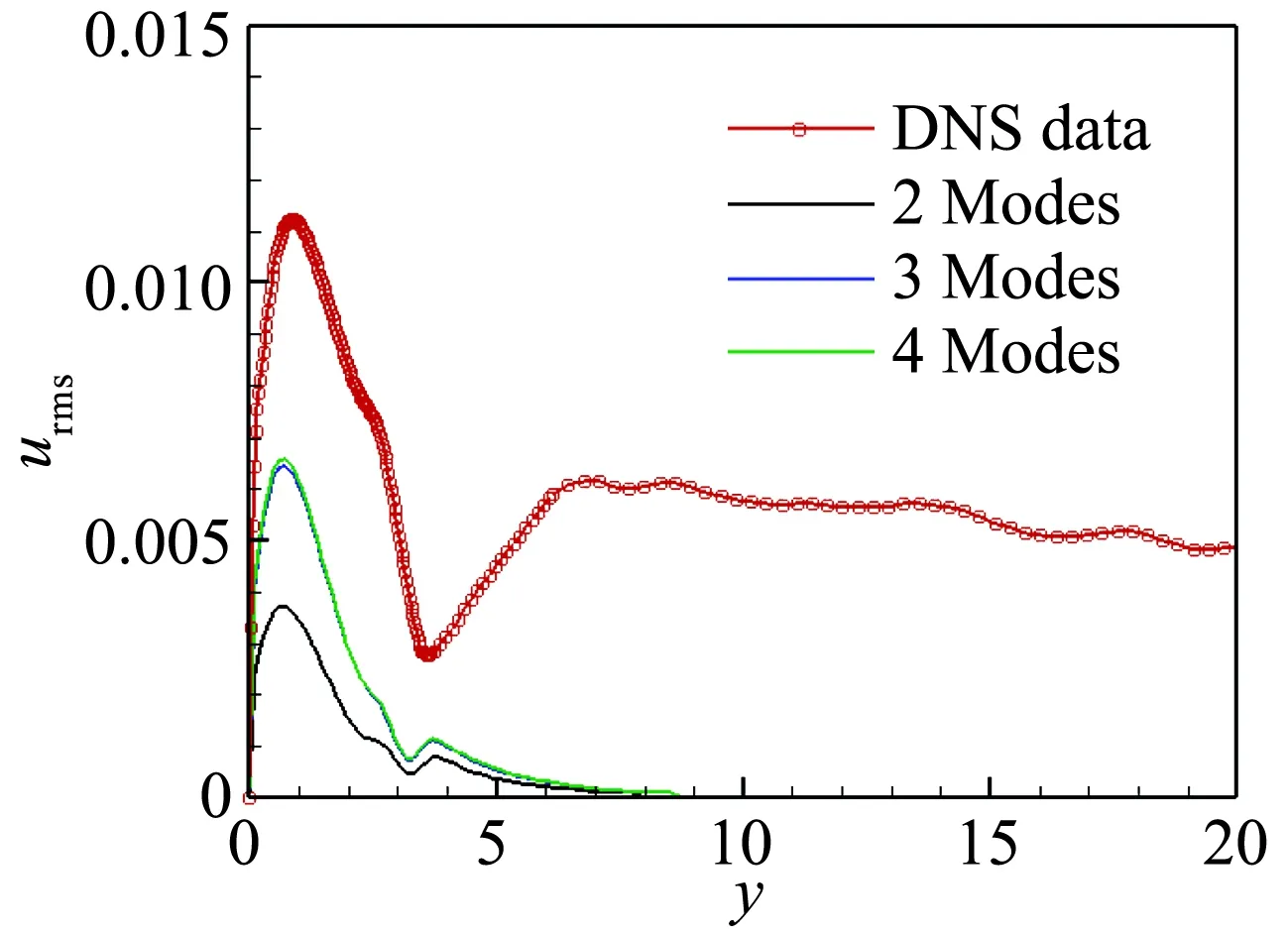
(b) 速度

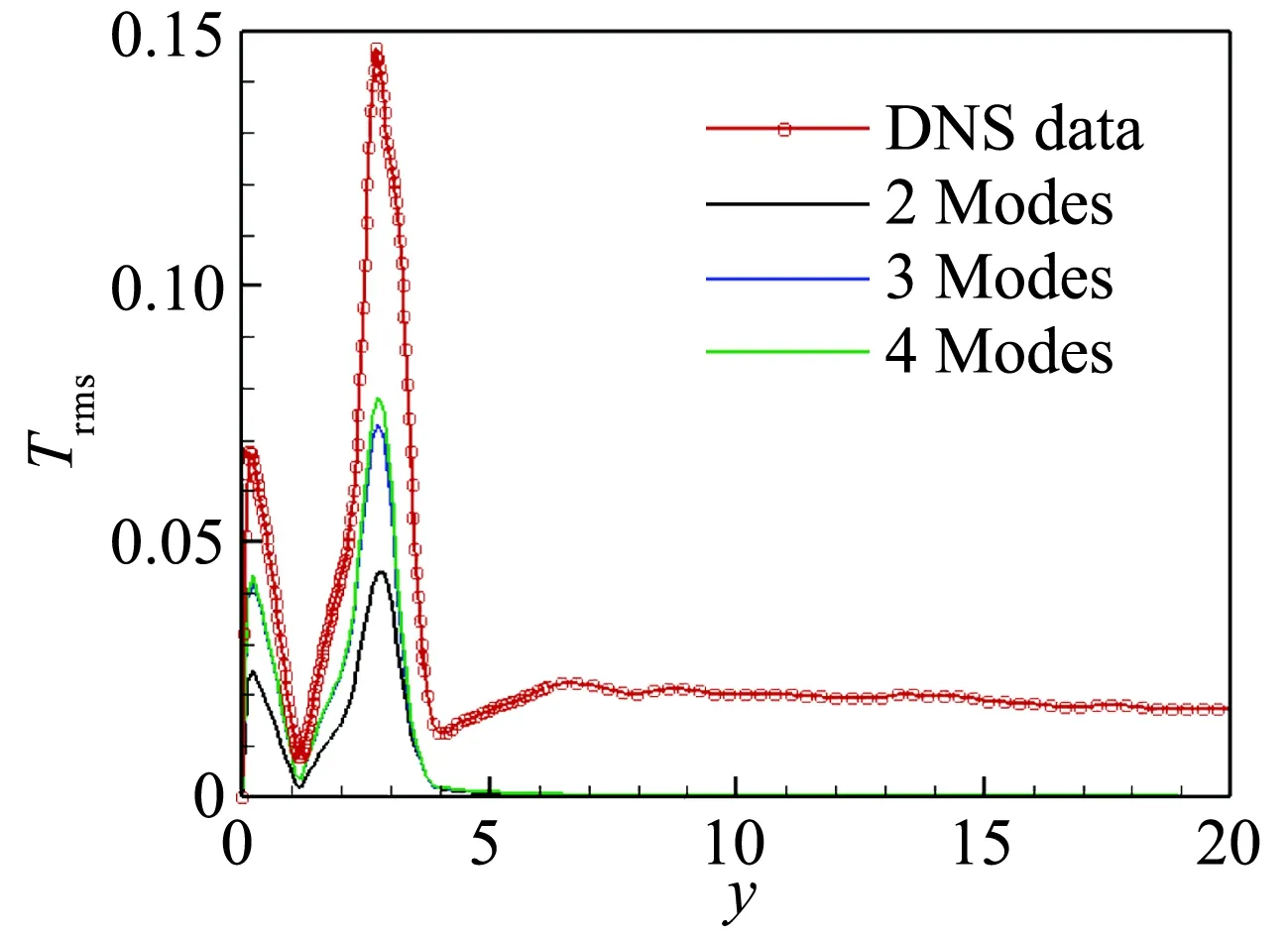
(c) 温度脉冲均方根

4 结 论

超声速和高超声速边界层转捩中存在多种不同的物理机制，其相互作用复杂，模态分析是研究这一问题的重要工具。本文对Ma=2.25和Ma=6边界层流动转捩后期的流场进行动力模态分解，并对模态进行分析讨论，重点考察了模态中流场的结构和壁面阻力和热流的关系。计算和分析结果表明，超声速边界层转捩后期的流动与不可压缩和亚声速流动相似，在转捩后期以低频的流向涡结构为主，对壁面阻力和热流的变化起主要作用；高频小尺度结构则是低频流向涡的衍生物，在转捩开始后才对壁面阻力和热流有比较重要的作用；高超声速边界层转捩中存在多种不稳定模态，低频模态的流场结构为流向条带，高频的模态流场结构为二维扰动波，低频模态是由高频模态诱导产生的。高低频模态之间的相互作用可以通过条件统计和相关性分析等手段得出，这一方面的研究正在进行。

致谢:感谢清华信息科学与技术国家实验室(筹)公共平台与技术部提供的计算机时。

参考文献：

[1]Xie S F, Yang W B, Shen Q.Review of progresses in hypersonic boundary layer transition mechanism and its applications[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 714- 723.(in Chinese)解少飞, 杨武兵, 沈清.高超声速边界层转捩机理及应用的若干进展回顾[J].航空学报, 2015, 36(3): 714-723.

[2]Luo J S.Transition and prediction for hypersonic boundary layers[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357-372.(in Chinese)罗纪生.高超声速边界层的转捩及预测[J].航空学报, 2015, 36(01): 357-372.

[3]Chen J Q, Tu G H, Zhang Y F, et al.Hypersnonic boundary layer transition: what we know, where shall we go[J].Acta Aerodynamica Sinica, 2017, 35(3): 311-337.(in Chinese)陈坚强, 涂国华, 张毅锋, 等.高超声速边界层转捩研究现状与发展趋势[J].空气动力学学报, 2017, 35(3): 311-337.

[4]Cao W.A study of the transition prediction of hypersonic boundary layer on plane and wedge flow[J].Acta Aerodynamica Sinica, 2009, 27(5): 516-523.(in Chinese)曹伟.高超声速边界层的转捩问题[J].空气动力学学报, 2009, 27(5): 516-523.

[5]Rowley C W, Dawson S T M.Model reduction for flow analysis and control[J].Annual Review of Fluid Mechanics, 2017, 49: 387-417.

[6]Schmid P J.Dynamic Mode decomposition of numerical and experimental data[J].Journal of Fluid Mechanics, 2010, 656: 5-28.

[8]He G, Wang J, Pan C.Initial growth of a disturbance in a boundary layer influenced by a circular cylinder wake[J].Journal

of Fluid Mechanics, 2013, 718: 116-130.

[9]Subbareddy P K, Bartkowicz M D, Candler G V.Direct numerical simulation of high-speed transition due to an isolated roughness element[J].Journal of Fluid Mechanics, 2014, 748: 848-878.

[10]Sayadi T, Schmid P J, Nichols J W, et al.Reduced-order representation of near-wall structures in the late transitional boundary layer[J].Journal of Fluid Mechanics, 2014, 748: 278-301.

[11]傅德薰, 马延文, 李新亮.可压缩湍流直接数值模拟[M].北京: 科学出版社, 2010.

[12]Li X L.Direct numerical simulation techniques for hypersonic turbulent flows[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 147-158.(in Chinese)李新亮.高超声速湍流直接数值模拟技术[J].航空学报, 2015, 36(01): 147-158.

[13]Li X L, Fu D X, Ma Y W, et al.Acoustic calculation for supersonic turbulent boundary layer flow[J].Chinese Physics Letters, 2009, 26(9): 094701.

[14]Li X L, Fu D X, Ma Y W.Direct numerical simulation of a spatially evolving supersonic turbulent boundary layer atMa= 6[J].Chinese Physics Letters, 2006, 23(6): 1519.

[15]Pirozzoli S, Grasso F, Gatski T B.Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer atM=2.25[J].Physics of Fluids, 2004, 16(3): 530-545.

[16]Williams J E F, Maidanik G.The Mach wave field radiated by supersonic turbulent shear flows[J].Journal of Fluid Mechanics, 1965, 21(4): 641-657.

[17]Duan L, Beekman I, Martin M P.Direct numerical simulation of hypersonic turbulent boundary layers.Part 3.Effect of Mach number[J].Journal of Fluid Mechanics, 2011, 672: 245-267.

[18]Tu J H, Rowley C W, Luchtenburg D M, et al.On dynamic Mode decomposition: theory and applications[J].arXiv preprint arXiv: 1312.0041, 2013.

[20]Li X, Fu D, Ma Y.Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J].Physics of Fluids (1994-present), 2010, 22(2): 025105.